数字信号处理之FFT终极理解

本节从离散傅里叶变换的深入理解说起，介绍了FFT的基本原理，其中包括基2、基4的按时间抽选FFT算法和按频率抽取FFT算法

从DFT说起

• DFT的基本公式：
  $$
  X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk},k=0,1,…,N-1
  $$

  $$
  W_N^{nk}=e^{-j\frac{2\pi}{N}nk}
  $$

• 看这个公式里面有个$\frac{2\pi}{N}$，有没有觉得很熟悉，哦没错，它其实就是数字角频率$w_0$（这个在我的其他笔记中有提到信号处理中的小知识点 | ssy的小天地 (ssy1938010014.github.io)）

  • 那么该如何理解它呢？正如在之前笔记中提到的，它代表在复数平面内每个点转过的角度

    

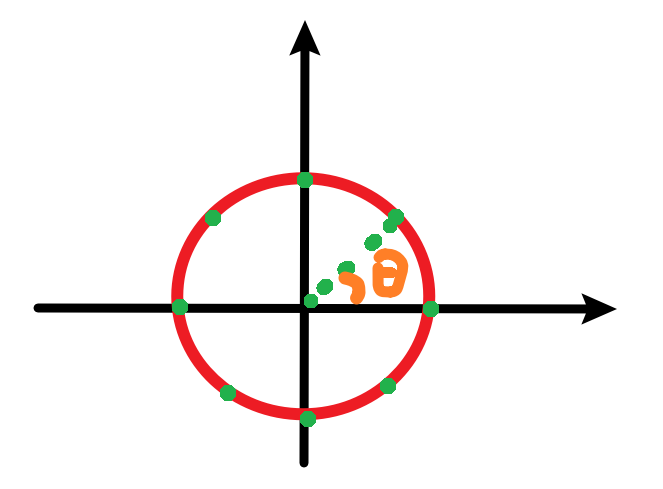
  • 图中标出的$\theta$，其实就是数字角频率$w_0$，在对一个正弦波抽样后，得到的点，其实就没有时间的概念了，只是我们自己心里清楚，点与点之间的时间间隔是$T_s$（采样间隔）

  • 那么如何数字角频率和实际模拟信号的角频率是如何对应的呢？即在之前笔记中提到的：$\Omega_0=w_0f_s$，那对于频域来说，旋转因子中的角频率不能只有$w_0$，不然就只能测出$w_0$对应模拟信号的频率，类似DTFT的基频和倍频，这里我们也多取一些角频率$w_0,2w_0,3w_0,…(N-1)w_0$，也就是$kw_0,k=0,1,…,N-1$。理想情况下，如果在频域$kw_0$有个冲击，那么就说明对应时域信号中含有角频率为$kw_0f_s=k\frac{2\pi}{N}f_s=2\pi\cdot \frac{kf_s}{N}$的正弦信号，即频率为$k\frac{f_s}{N}$的正弦信号（其实，这也从公式本质的切入点上，解释了数字k域与实际时域频率的对应关系）

  • 上述一大段的解释可能也有误，但是我自己最极限的理解了，如果不理解也没关系，我觉得这里只需要记住：以角频率$w_0$每隔$T_s$时间在复数域内转动的N点（其在实轴上的投影就是$cos(\frac{2\pi}{N}n)$，其本身就是复数$e^{j\frac{2\pi}{N}n}$），在经过DFT之后，可以得到这个N点数字域对应模拟域的实际频率$f_0$，且$f_0=k\cdot \frac{f_s}{N}$

• 下面重点解释为啥$x(n)$与$e^{-j\frac{2\pi}{N}nk}$这么个玩意相乘，就能挑选出对应频率（这些解释都偏个人的感性解释，也不一定完全正确）

  • 首先，假设$x(n)=cos(\frac{2\pi}{N}n)$，$x(k)$就等于$k$确定情况下，$n=0\sim N-1$个$x(n)$对应的点与旋转因子中$e^{-j\frac{2\pi}{N}n},n=0\sim N-1$对应元素相乘（例如$x(0)\times e^{-j\frac{2\pi}{N}\cdot 0\cdot k},x(1)\times e^{-j\frac{2\pi}{N}\cdot 1\cdot k},x(2)\times e^{-j\frac{2\pi}{N}\cdot 2\cdot k},…$）。简单来说，这一步骤就是：在$k$（也就是某一频率）下，求信号对这一频率幅频特性曲线的贡献（这么说可能不太规范，通俗来讲，就是如果信号中含有这个频率，那么它的幅频特性曲线中，这个频率对应的幅度就会格外高，也就是说这一步就是在求这个幅度到底有多高）

  • 此时，你会发现，有个离谱的事情发生了$x(n)$是个$cos$，$e^{j\frac{2\pi}{N}n}$是个复数，这咋乘，就现在，我发现了欧拉的伟大，应用欧拉公式，有：
    $$
    cos(\frac{2\pi}{N}n)=\frac{e^{j\frac{2\pi}{N}n}+e^{-j\frac{2\pi}{N}n}}{2}
    $$

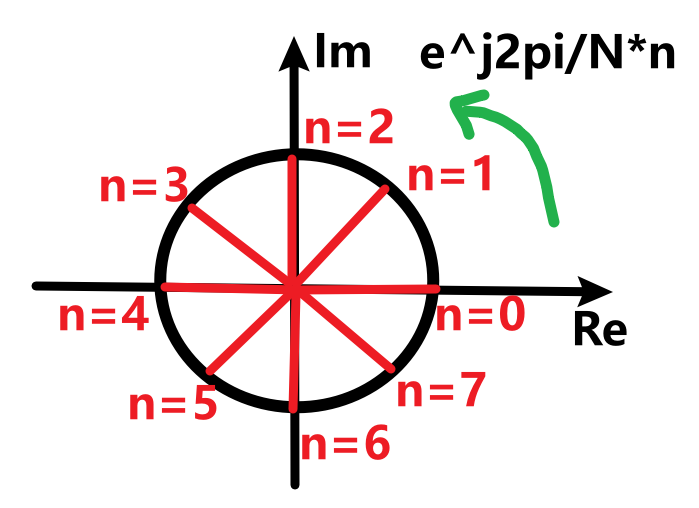
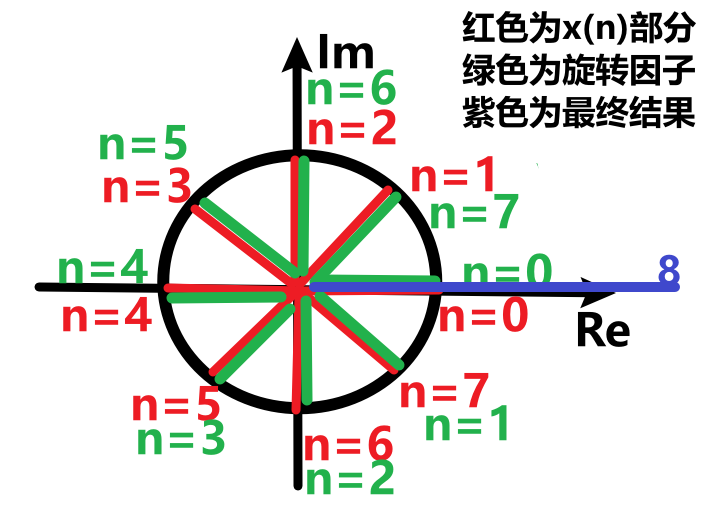
  • 现在是不是cos就能和复数相乘了，为了便于解释，假设$N=8$，那么$e^{j\frac{2\pi}{N}n}$在复平面上的8个点（图1）为：

    

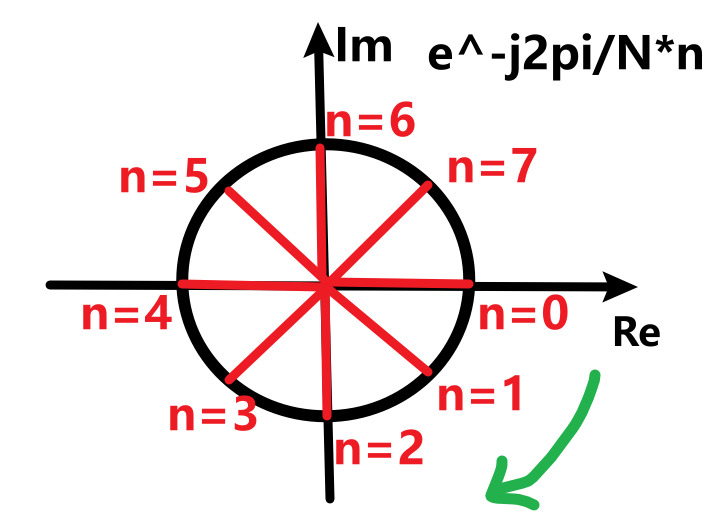
  • $e^{-j\frac{2\pi}{N}n}$在复平面上的8个点（图2）为：

    

  • 当$k=1$时，$W_N^{n}=e^{-j\frac{2\pi}{N}n}$，其在复平面上的8个点（图3）为：

    

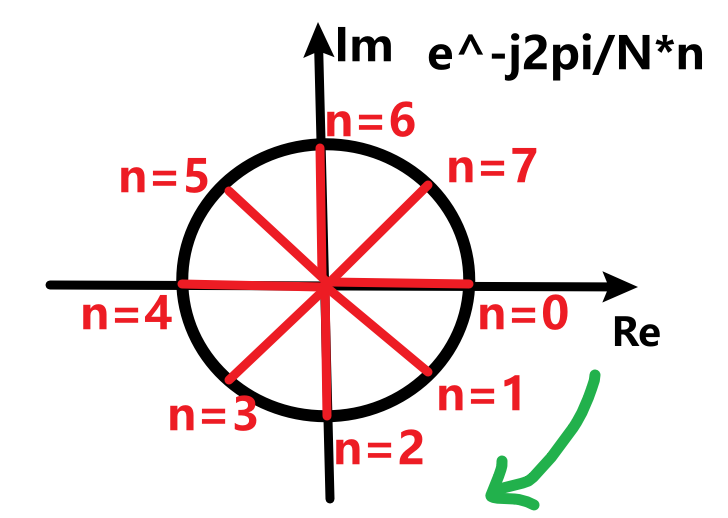
    • 图1中8个复数乘以图3中对应的复数（例如图1中n=1的复数乘以图3中n=1中的复数，图1中n=2的复数乘以图3中n=2中的复数），显然，每个点对点的相乘，其均是模值相乘，由于角度相反，那么相乘后相位为0，最终这8个点对点相乘求和的结果就是8，可视化示意图如下：

      

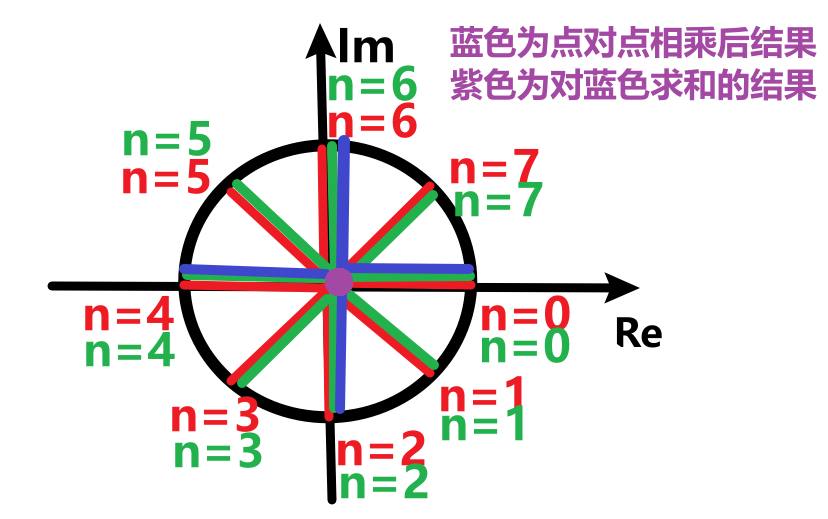
    • 同样，图2中8个复数乘以图3中对应的复数，每个点对点结果是模值相乘，旋转角变为原来两倍，对结果求和后，最终为0

      

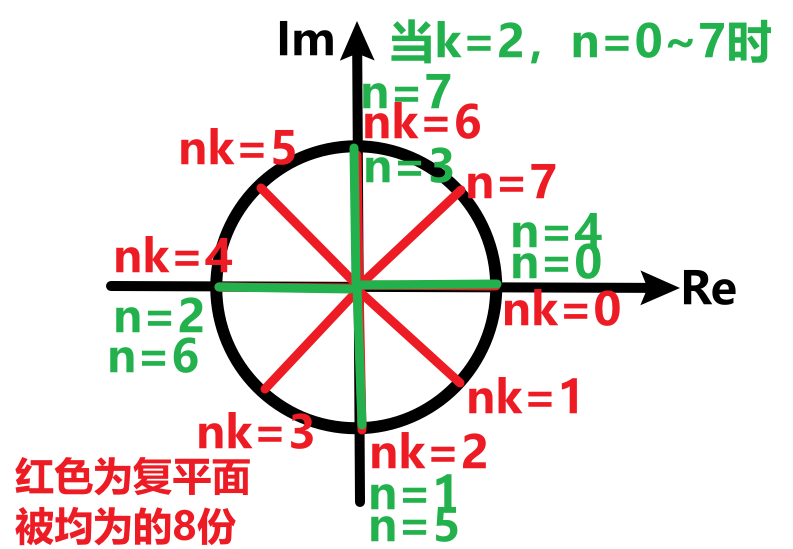
  • 其实，$W_N^{nk}=e^{-j\frac{2\pi}{N}nk}$就是将复平面均匀分成8份，由$nk$决定，具体对应是八份中的哪一份，当$k=2$时，$nk$为$0,2,4,6,8,10,12,14$，由于8个点就转了一圈，即周期时8，那么$nk$实际对应的是$0,2,4,6,0,2,4,6$，其可视化示意如下（图4）：

    
    • 将图1与图4中n相同的点对应相乘，根据模值相乘，角度相加的原则，最终矢量相加的结果为0，图2乘以图4的结果也为0

  • 同理，当$k=3,4,5,6$时（$k=7$的情况后面会解释，存在对称性），图1乘以图4，图2乘以图4的结果均为0（这里没有严格上的数学推导，但我觉得对于理解FFT，自己带数进去算一遍更能理解）

  • 总之，最后我们会发现：只有$e^{j\frac{2\pi}{N}n}$乘以$W_N^{nk}(k=1)$有值，其值为$e^{j\frac{2\pi}{N}n}$每个点的模值（这里都假设为1了）与$W_N^{nk}$对应点的模值（显然$W_N^{nk}$的模都是1）相乘后再求和（还要除以2，因为欧拉公式后$e^{j\frac{2\pi}{N}n}$前的系数为$\frac12$），其实，$e^{j\frac{2\pi}{N}n}$每个点的模值都一样，你想，$cos(\frac{2\pi}{N}n)$和$5cos(\frac{2\pi}{N}n)$用欧拉公式展开之后，不就是$e^{j\frac{2\pi}{N}n}$和$5e^{j\frac{2\pi}{N}n}$的区别么，那么实际上每个点的模值都是一样的，即$(1,1,1,1,1,1,1,1)$和$(5,5,5,5,5,5,5,5)$，那么实际上$cos(\frac{2\pi}{N}n)$乘以$W_N^{nk}$就是$\frac{A\times N}{2}$（其中$A$为正弦信号的幅度，$N$为采样的点数），这个峰值会出现在$k=1$的位置（这里的解释都先不讨论$k=7$的情况）

  • 哦对了，其实这里也很好的解释了采样点数$N$加倍，DFT结果幅值也会加倍

  • 有个细节是，当$k=0$时，很容易得到$cos(\frac{2\pi}{N}n)$乘以$W_N^{nk}$是16（因为不管是$e^{j\frac{2\pi}{N}n}$还是$e^{-j\frac{2\pi}{N}n}$都是一堆111去乘以$W_N^{nk}$的一堆1嘛），所以这也解释了零频对应的峰值是其他频率峰值的两倍

• 下面解释DFT的共轭对称性，即$X(k)=X^*(N-k)$

  • 那么我们来讨论$k=7$的情况，$W_N^{7n}=e^{-j\frac{2\pi}{N}n\cdot7}$，其在复平面上的8个点（图5）为：

    

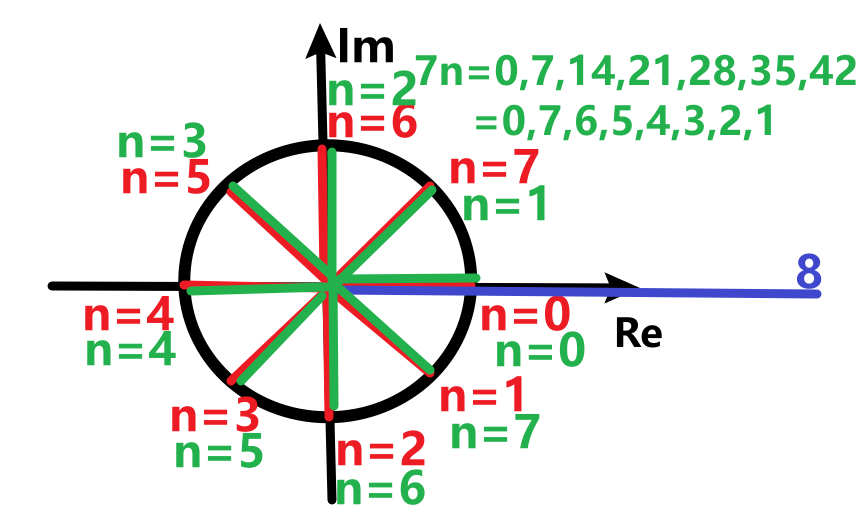
  • 不难发现，$k=7$时的情况刚好和$k=1$的情况是反过来的，此时是$e^{-j\frac{2\pi}{N}n}$乘以$W_N^{nk}$有值（且也为$\frac{A\times N}{2}$），$e^{j\frac{2\pi}{N}n}$乘以$W_N^{nk}$为0，所以频谱中还会在$k=7$时再出现一个峰值

  • 同时也解释了为什么复数信号的DFT是单边谱，因为复数信号只有$e^{j\frac{2\pi}{N}n}$部分，只存在$e^{j\frac{2\pi}{N}n}$乘以$W_N^{nk}$的结果，故复数信号只有单边谱（换句话来说，实数信号的双边谱多余的那边是$e^{-j\frac{2\pi}{N}n}$造成的）

  • 笑了，上面解释一大堆，其实就是用了旋转因子的对称性：$(W_N^{nk})^*=W_N^{-nk}=W_N^{(N-n)k}$

---

按时间抽选FFT算法

1.基2-FFT算法

• 设序列$x(n)$点数为$N=2^L$，$L$为正整数

• 将序列$x(n)$按$n$的奇偶分为以下两组：
  $$
  偶序列:x(2r)=x_1(r),r=0,1,…,\frac N2-1
  $$

  $$
  奇序列:x(2r+1)=x_2(r),r=0,1,…,\frac N2-1
  $$

• 则其$N$点FFT为：
  $$
  \begin{aligned}
  X(k) &= \sum_{n=0}^{N-1}x(n)W_N^{nk}\
  &=\sum_{n=0}^{\frac N2-1}x(2r)W_N^{2rk}+\sum_{n=0}^{\frac N2-1}x(2r+1)W_N^{(2r+1)k}\
  &=\sum_{n=0}^{\frac N2-1}x_1(r)W_N^{2rk}+\sum_{n=0}^{\frac N2-1}x_2(r)W_N^{(2r+1)k}\
  &=\sum_{n=0}^{\frac N2-1}x_1(r)W_{\frac N2}^{rk}+W_N^k\sum_{n=0}^{\frac N2-1}x_2(r)W_{\frac N2}^{2rk}\
  &= X_1(k)+W_N^kX_2(k)
  \end{aligned}
  $$

  • 其中有用到旋转因子的约分性$W_N^m=W_{\frac N2}^{\frac m2}$
  • 且$X_1(k)$和$X_2(k)$分别是$x_1(r)$和$x_2(r)$的$\frac N2$点DFT

• 对于$X(k+\frac N2)$，有：
  $$
  X(k+\frac N2) = X_1(k+\frac N2)+W_N^{k+\frac N2}X_2(k+\frac N2)\
  $$

  • 我们知道，频谱也是有周期的，以N（参与傅里叶变换的点数）个点为周期，对于DFT只是取了最中心的一个周期，而$X_1(k)$和$X_2(k)$都是$\frac N2$点DFT，故：
    $$
    X_1(k)=X_1(k+\frac N2)
    $$

    $$
    X_2(k)=X_2(k+\frac N2)
    $$

  • 根据旋转因子的性质有：
    $$
    W_N^{(k+\frac N2)}=W_N^k\cdot W_N^{\frac N2}=-W_N^k
    $$

    • 因为$W_N^{\frac N2}=-1$

  • 所以，最终$X(k+\frac N2)$的结果为：
    $$
    X(k+\frac N2) = X_1(k)-W_N^kX_2(k)
    $$

• 整理上述推导，可以得到：
  $$
  \begin{cases}
  \begin{aligned}
  X(k) &= X_1(k)+W_N^kX_2(k)\
  X(k+\frac N2) &= X_1(k)-W_N^kX_2(k)
  \end{aligned}
  \end{cases},k=0,1,…,\frac N2-1
  $$

  • 这个式子画成信号流图就是一个蝶形变换，每求一个点的频谱，都需要知道对应偶序列的一个点和奇序列的一个点

• 根据上式可知，只要能求出$k=0,1,…,\frac N2-1$对应的频谱，就可以同时得到$k=\frac N2,\frac N2+1,\frac N2+2,…,N-1$的频谱

  • 那么，如何得到频谱中前一半的值呢？根据公式，只需要能求出$X_1(k)$和$X_2(k)$就搞定了，而$X_1(k)$和$X_2(k)$是偶序列和奇序列的傅里叶变换，貌似也求不出来，那么就继续分解$X_1(k)$和$X_2(k)$

  • 将$X_1(k)$对应的序列又分为偶序列和奇序列，$X_2(k)$对应的序列又分为偶序列和奇序列

  • 一直这么分解下去，直到时域上只有两个点，2点DFT（这也称为蝶形变换）我们还是很容易得到的，即：

    $$ X(0)=x(0)+x(1) $$

    $$
    X(1)=x(0)-x(1)
    $$

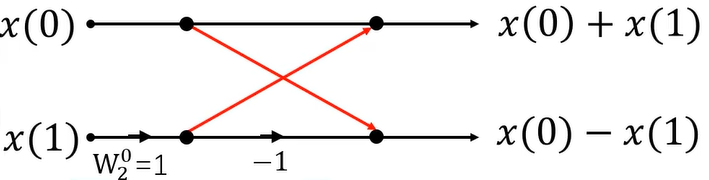
  • 得到这两个点的DFT，我们就得到了4个点偶序列和奇序列的DFT，进而可以求出4个点的DFT，以此类推，从而可以求出更高点数的DFT

  • 也就是说，我们对时域序列进行偶序列和奇序列分类，再对这个偶序列进行偶序列和奇序列分类，对这个奇序列进行偶序列和奇序列分类，分到最后时域上的序列两两一组，然后依次往下求蝶形变换，就可以得到最终N个序列的DFT结果，举一个8点FFT的例子，先画一个时域上两两分组的示意图：

    

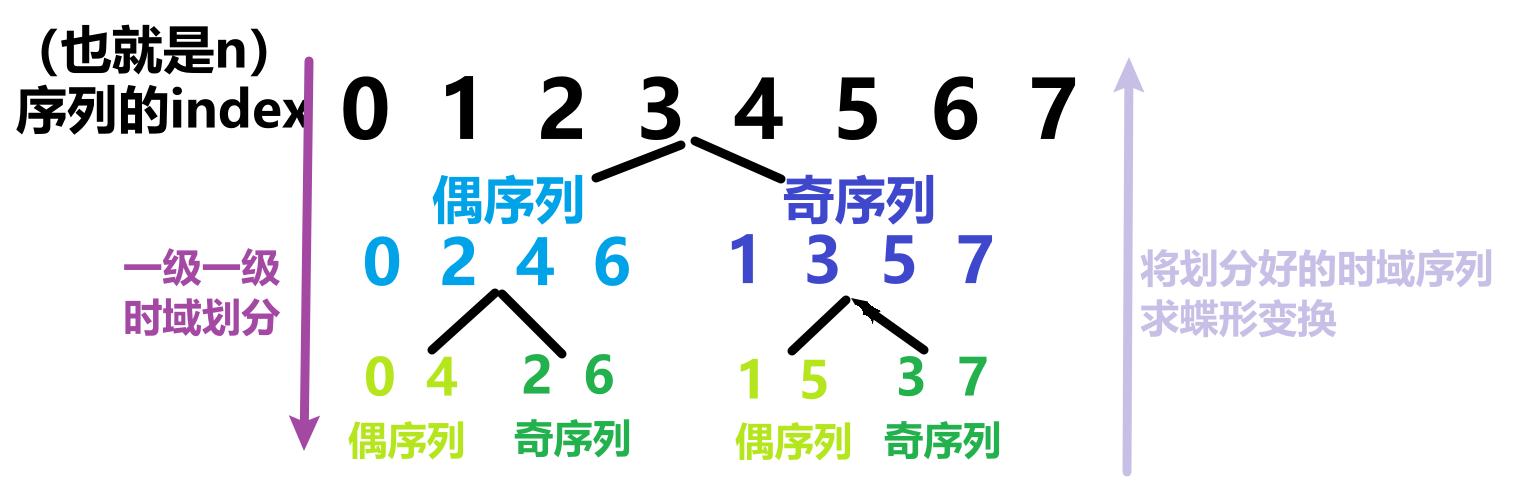
  • 一个标准的8点基2-FFT流图如下：

    

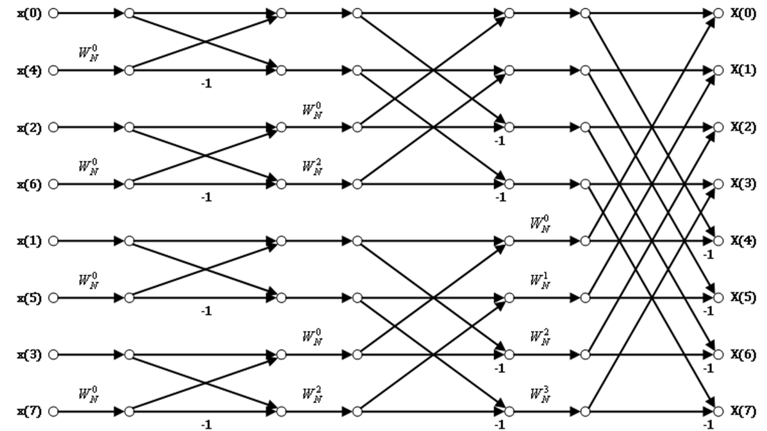
• 所以简单概括来说，基2-FFT算法是，计算一个N点DFT时，先需要计算两个$\frac N2$点DFT，然后对每个$\frac N2$点DFT，继续往下划分，还需要计算2个$\frac N4$点DFT（总共这一层就有4个$\frac N4$点DFT结果），直至最后分解到$\frac N{2^k}$（$k$表示第k次分解）=2时（容易通过这个等式得到$k=log_2^{\frac N2}$），我们就能迅速计算出第$k$次分解后$2^k$个2点DFT的结果（这里单纯用数学归纳法都能计算出第$k$次分解后需要计算的DFT个数为$2^k$），之后我们就可以反推回去，得到$N$点DFT的结果

• N点基2-FFT的计算量：

  • 蝶形级数：$M=log_2^N$
  • 每级的蝶形数量：$\frac N2$
  • 每个蝶形的计算量：
    • 加法2次
    • 乘法1次
  • 总共的计算量：
    • 加法：$Nlog_2^N$
    • 乘法：$\frac N2 log_2^N$

2.基4-FFT算法

• 设序列$x(n)$点数为$N=4^L$，$L$为正整数

• 将$N=4^L$分为以下4组：
  $$
  \begin{cases}
  \begin{aligned}
  x(4r) &= x_1(r)\
  x(4r+1) &= x_1(r)\
  x(4r+2) &= x_1(r)\
  x(4r+3) &= x_1(r)
  \end{aligned}
  \end{cases},r=0,1,…,\frac N4 -1
  $$

• 则其$N$点DFT为：
  $$
  \begin{aligned}
  X(k)&=\sum_{n=0}^{N-1}x(n)W_N^{nk}\
  &= \sum_{r=0}^{\frac N4-1}x(4r)W_N^{4rk}+\sum_{r=0}^{\frac N4-1}x(4r+1)W_N^{(4r+1)k}+\sum_{r=0}^{\frac N4-1}x(4r+2)W_N^{(4r+2)k}+\sum_{r=0}^{\frac N4-1}x(4r+3)W_N^{(4r+3)k}\
  &= \sum_{r=0}^{\frac N4-1}x_1(r)W_{\frac N4}^{rk}+W_N^k\sum_{r=0}^{\frac N4-1}x_2(r)W_{\frac N4}^{rk}+W_N^{2k}\sum_{r=0}^{\frac N4-1}x_3(r)W_{\frac N4}^{rk}+W_{\frac N4}^{3k}\sum_{r=0}^{\frac N4-1}x_4(r)W_{\frac N4}^{rk}\
  &= X_1(k)+W_N^kX_2(k)+W_N^{2k}X_3(k)+W_N^{3k}X_4(k)
  \end{aligned}
  $$

  • 其中$X_1(k),X_2(k),X_3(k),X_4(k)$分别是$x_1(r),x_2(r),x_3(r),x_4(r)$的$\frac N4$点DFT

• 由于$W_N^k$有以下性质：
  $$
  W_N^{(k+\frac N4)}=W_N^{\frac N4}W_N^k=-jW_N^k
  $$

  $$
  W_N^{(k+\frac N2)}=W_N^{\frac N2}W_N^k=-W_N^k
  $$

  $$
  W_N^{(k+\frac {3N}4)}=W_N^{\frac {3N}4}W_N^k= jW_N^k
  $$

• 故有：
  $$
  \begin{cases}
  \begin{aligned}
  X(k) &= X_1(k)+W_N^kX_2(k)+W_N^{2k}X_3(k)+W_N^{3k}X_4(k)\
  X(k+\frac N4) &= X_1(k)-jW_N^kX_2(k)-W_N^{2k}X_3(k)+jW_N^{3k}X_4(k)\
  X(k+\frac N2) &= X_1(k)-W_N^kX_2(k)+W_N^{2k}X_3(k)-W_N^{3k}X_4(k)\
  X(k+\frac {3k}{4}) &= X_1(k)+jW_N^kX_2(k)-W_N^{2k}X_3(k)-jW_N^{3k}X_4(k)
  \end{aligned}
  \end{cases},k=0,1,…,\frac N4 -1
  $$

• 与之基2类似，计算一个N点DFT时，先需要计算4个$\frac N4$点DFT，然后对每个$\frac N4$点DFT，继续往下划分，还需要计算4个$\frac{N}{16}$点DFT（总共这一层就有16个$\frac N{16}$点DFT结果），直至最后分解到$\frac N{4^k}$=4时（容易通过这个等式得到$k=log_4^{\frac N4}$），我们就能比较容易计算出第$k$次分解后$4^k$个4点DFT的结果（这里单纯用数学归纳法都能计算出第$k$次分解后需要计算的DFT个数为$4^k$），之后我们就可以反推回去，得到$N$点DFT的结果（只是这里反推时乘以的旋转因子与基2时不太一样，这里的蝶形运算是以4个点为基本单位）。

  • 以16点FFT为例，其运算过程的可视化示意图如下：（如果是64点FFT，就把下面这个图看成一个整体，复制粘贴4份分析）
  

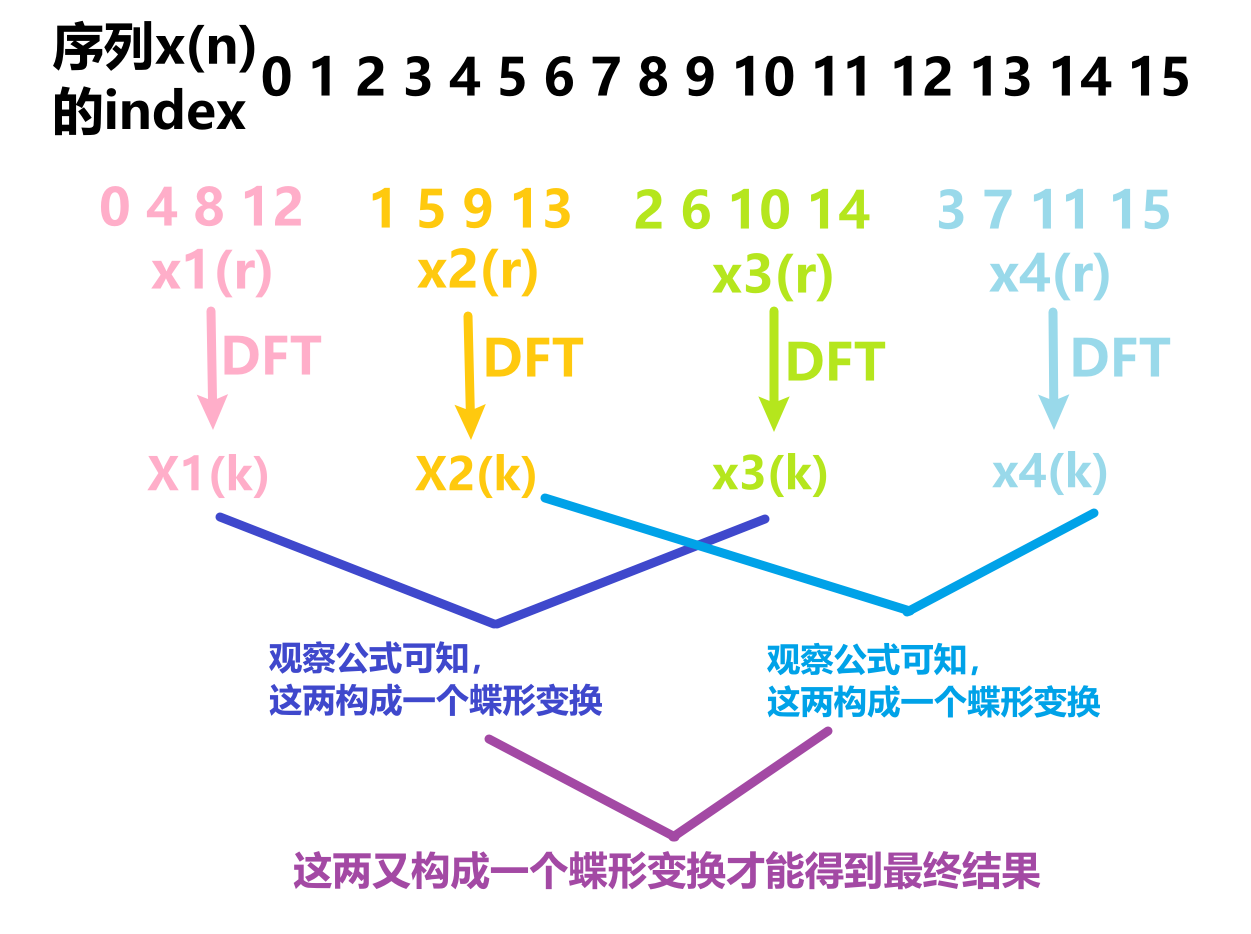
  • 图中第一层的4点DFT的算法和基2FF算法计算4点FFT一样

    

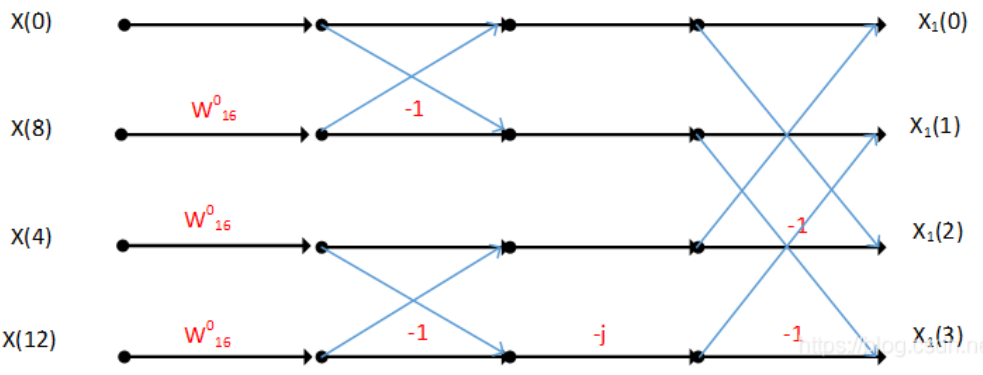
  • 将两幅图合起来理解就是：

    

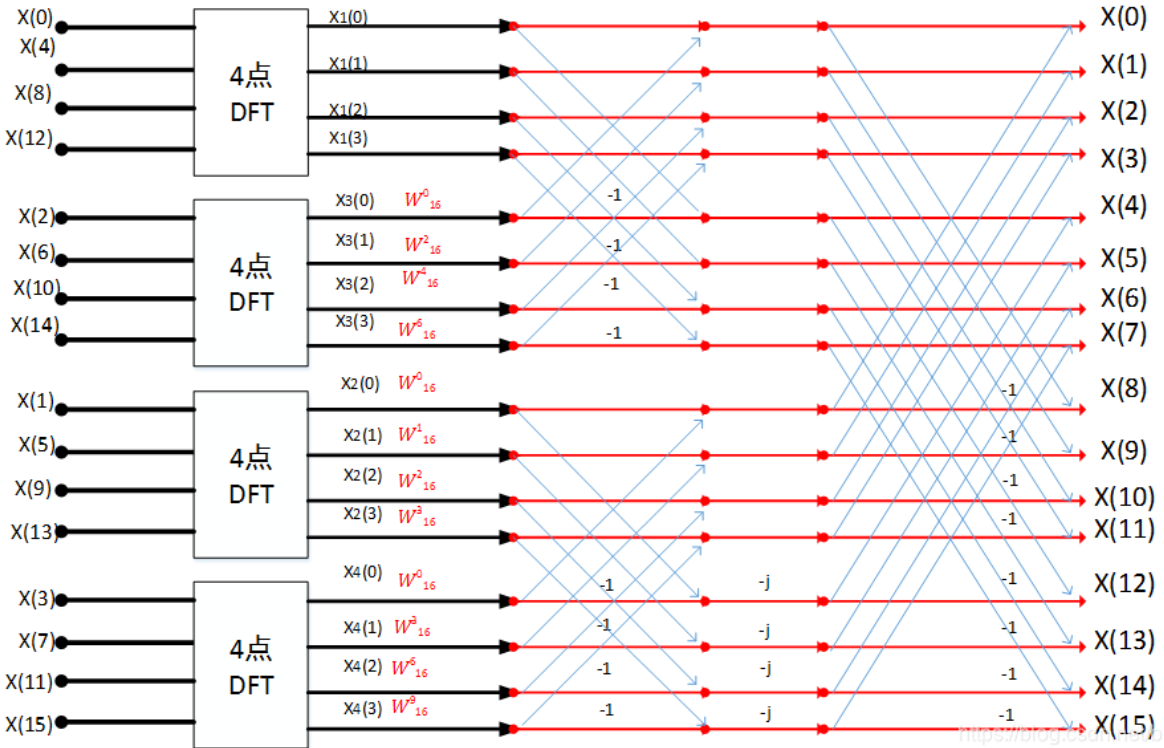
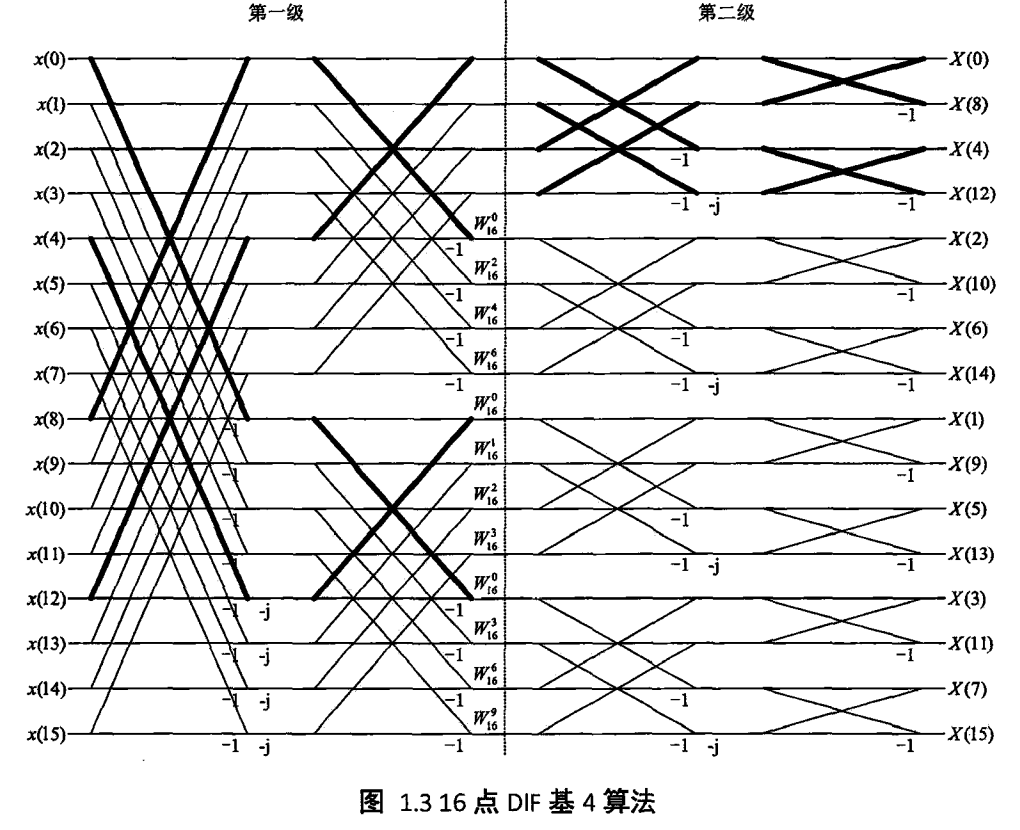
  • 一个标准的16点基4-FFT流程图如下：

    

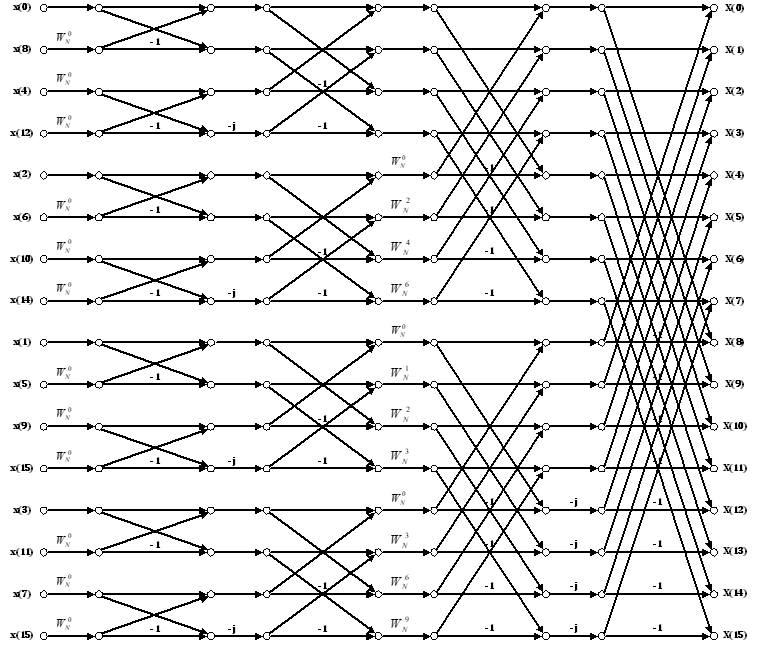
• N点基4-FFT的计算量：

  • 蝶形级数：$M=log_4^N$
  • 每级的蝶形数量：$\frac N4$
  • 每个蝶形运算有4点输入和4点输出，则：
    • 加法8次
    • 乘法3次
  • 总共的计算量：
    • 加法：$2Nlog_4^N$
    • 乘法：$\frac {3N}4 log_4^N$

---

按频率抽选FFT算法

1.基2-FFT算法

• 设序列$x(n)$点数为$N=2^L$，$L$为正整数

• 将序列按$n$的顺序分为前后两组，其$N$点DFT为：
  $$
  \begin{aligned}
  X(k)&=\sum_{n=0}^{N-1}x(n)W_N^{nk}\
  &=\sum_{n=0}^{\frac N2-1}x(n)W_N^{nk}+\sum_{n=\frac N2}^{N-1}x(n)W_N^{nk}\
  &= \sum_{n=0}^{\frac N2 -1}x(n)W_N^{nk}+\sum_{n=0}^{\frac N2-1}x(n+\frac N2)W_N^{(n+\frac N2)k}\
  &= \sum_{n=0}^{\frac N2-1}[x(n)+x(n+\frac N2)W_N^{\frac N2k}]W_N^{nk}\
  &= \sum_{n=0}^{\frac N2-1}[x(n)+(-1)^kx(n+\frac N2)]W_N^{nk}
  \end{aligned}
  $$

• 按$k$的奇偶可将$X(k)$分为两部分：
  $$
  \begin{cases}
  \begin{aligned}
  k &= 2r\
  k &= 2r+1
  \end{aligned}
  \end{cases},k=0,1,…,\frac N2-1
  $$

• 则有：
  $$
  \begin{aligned}
  X(2r)&=\sum_{n=0}^{\frac N2 -1}[x(n)+x(n+\frac N2)]W_N^{2nr}\
  &=\sum_{n=0}^{\frac N2 -1}[x(n)+x(n+\frac N2)]W_{\frac N2}^{nr}
  \end{aligned}
  $$

  $$
  \begin{aligned}
  X(2r+1)&=\sum_{n=0}^{\frac N2 -1}[x(n)-x(n+\frac N2)]W_N^{n(2r+1)}\
  &=\sum_{n=0}^{\frac N2 -1}[x(n)-x(n+\frac N2)]W_N^nW_{\frac N2}^{nr}
  \end{aligned}
  $$

  • 令：
    $$
    \begin{cases}
    \begin{aligned}
    x_1(n)&=x(n)+x(n+\frac N2)\
    x_2(n)&=[x(n)-x(n+\frac N2)]W_N^n
    \end{aligned}
    \end{cases},n=0,1,…,\frac N2-1
    $$

• 则得到：
  $$
  \begin{cases}
  \begin{aligned}
  X(2r)&=\sum_{n=0}^{\frac N2-1}x_1(n)W_{\frac N2}^{nr}\
  X(2r+1)&=\sum_{n=0}^{\frac N2-1}x_2(n)W_{\frac N2}^{nr}
  \end{aligned}
  \end{cases},r=0,1,…,\frac N2-1
  $$

  • 仔细观察$\sum_{n=0}^{\frac N2-1}x_1(n)W_{\frac N2}^{nr}$这玩意不就是$x_1(n)$的$\frac N2$的DFT么

• 简而言之，有：
  $$
  X(k)的偶序列:X(2r)=DFT[x_1(n)]
  $$

  $$
  X(k)的奇序列:X(2r+1)=DFT[x_2(n)]
  $$

• 也就是$X(k)$的偶序列只跟$x_1(n)$（与时域序列对半分有关）的傅里叶变换有关，$X(k)$的奇序列只跟$x_2(n)$（与时域序列对半分有关）的傅里叶变换有关，那么问题的关键在于首先要知道$x_1(n)$和$x_2(n)$是啥，如果能将$x_1(n)$和$x_2(n)$继续往下分，使得最后只剩下两个点，那么做2点DFT就可以得到$X(k)$中2个点的DFT

  • 以8点FFT为例，整个运算过程的可视化示意图如下：
  

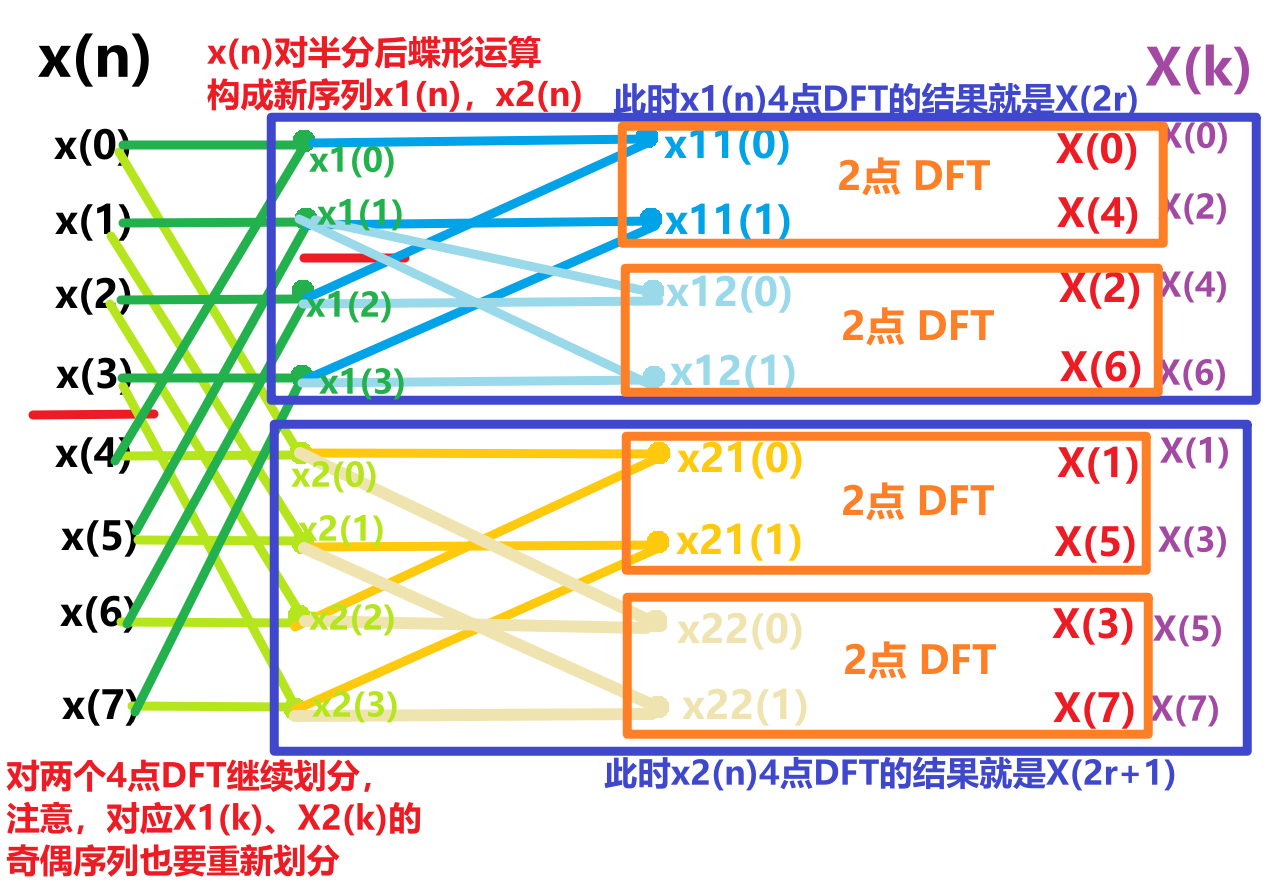
  • 下面是一个按频率抽选运算的完整的8点FFT流图：

    

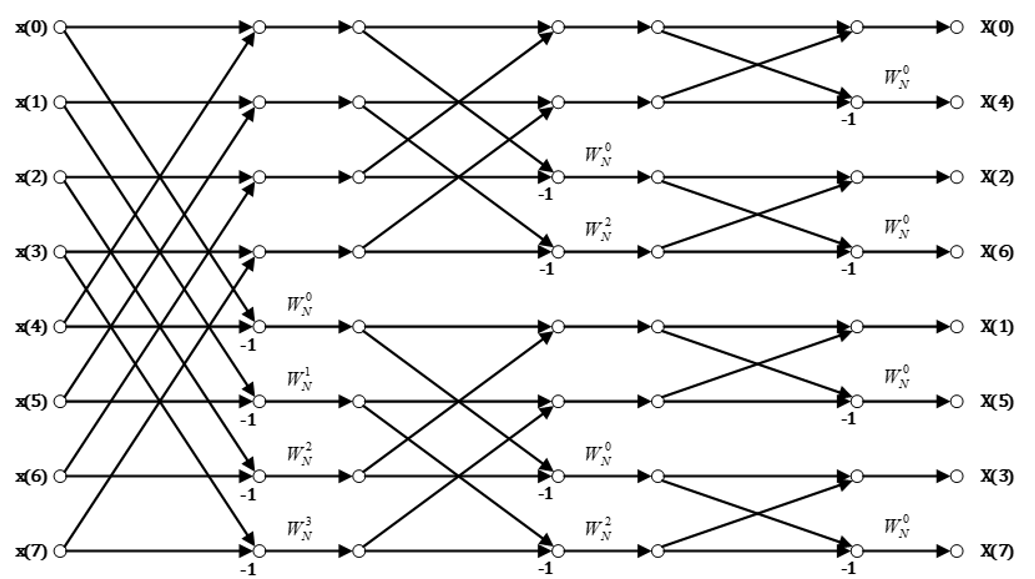
2.基4-FFT算法

• 设序列$x(n)$点数为$N=4^L$，$L$为正整数

• 将序列$x(n)$按$n$的顺序分为前后4组，其N点DFT为：
  $$
  \begin{aligned}
  X(k)&=\sum_{n=0}^{N-1}x(n)W_N^{nk}+\sum_{n=0}^{\frac N4-1}x(n)W_N^{nk}+\sum_{n=\frac N2}^{\frac {3N}4-1}x(n)W_N^{nk}+\sum_{n=\frac {3N}4}^{N-1}x(n)W_N^{nk}\
  &=\sum_{n=0}^{\frac N4-1}x(n)W_N^{nk}+\sum_{n=0}^{\frac N4-1}x(n+\frac N4)W_N^{(n+\frac N4)k}+\sum_{n=0}^{\frac N4-1}x(n+\frac N2)W_N^{(n+\frac N2)k}+\sum_{n=0}^{\frac N4-1}x(n+\frac {3N}4)W_N^{(n+\frac {3N}4)k}\
  &=\sum_{n=0}^{\frac N4-1}[x(n)+x(n+\frac N4)W_N^{\frac N4 k}+x(n+\frac N2)W_N^{\frac N2k}+x(n+\frac {3N}4)W_N^{\frac{3N}4k}]W_N^{nk}\
  &=\sum_{n=0}^{\frac N4-1}[x(n)+(-j)^kx(n+\frac N4)+(-1)^kx(n+\frac N2)+j^kx(n+\frac {3N}4)]W_N^{nk}
  \end{aligned}
  $$

• 按$k$将$X(k)$分为4部分：
  $$
  \begin{cases}
  \begin{aligned}
  k &= 4r\
  k &= 4r+1\
  k &= 4r+2\
  k &= 4r+3
  \end{aligned}
  \end{cases},r=0,1,…,\frac N4-1
  $$

• 则有：
  $$
  \begin{aligned}
  X(4r)&=\sum_{n=0}^{\frac N4-1}[x(n)+x(n+\frac N4)+x(n+\frac N2)+x(n+\frac {3N}4)]W_N^{4nr}\
  &=\sum_{n=0}^{\frac N4-1}[x(n)+x(n+\frac N4)+x(n+\frac N2)+x(n+\frac {3N}4)]W_{\frac N4}^{nr}
  \end{aligned}
  $$

  $$
  \begin{aligned}
  X(4r+1)&=\sum_{n=0}^{\frac N4-1}[x(n)-jx(n+\frac N4)-x(n+\frac N2)+x(n+\frac {3N}4)]W_N^{n(4r+1)}\
  &=\sum_{n=0}^{\frac N4-1}[x(n)-jx(n+\frac N4)-x(n+\frac N2)+x(n+\frac {3N}4)]W_N^nW_{\frac N4}^{nr}
  \end{aligned}
  $$

  $$
  \begin{aligned}
  X(4r+2)&=\sum_{n=0}^{\frac N4-1}[x(n)-x(n+\frac N4)+x(n+\frac N2)-x(n+\frac {3N}4)]W_N^{n(4r+2)}\
  &=\sum_{n=0}^{\frac N4-1}[x(n)-x(n+\frac N4)+x(n+\frac N2)-x(n+\frac {3N}4)]W_N^{2n}W_{\frac N4}^{nr}
  \end{aligned}
  $$

  $$
  \begin{aligned}
  X(4r+3)&=\sum_{n=0}^{\frac N4-1}[x(n)+jx(n+\frac N4)-x(n+\frac N2)-jx(n+\frac {3N}4)]W_N^{n(4r+3)}\
  &=\sum_{n=0}^{\frac N4-1}[x(n)+jx(n+\frac N4)-x(n+\frac N2)-jx(n+\frac {3N}4)]W_N^{3n}W_{\frac N4}^{nr}
  \end{aligned}
  $$

  • 令：
    $$
    \begin{cases}
    \begin{aligned}
    x_1(n)&=x(n)+x(n+\frac N4)+x(n+\frac N2)+x(n+\frac {3N}4)\
    x_2(n)&=[x(n)-jx(n+\frac N4)-x(n+\frac N2)+x(n+\frac {3N}4)]W_N^n\
    x_3(n)&=[x(n)-x(n+\frac N4)+x(n+\frac N2)-x(n+\frac {3N}4)]W_N^{2n}\
    x_4(n)&=[x(n)+jx(n+\frac N4)-x(n+\frac N2)-jx(n+\frac {3N}4)]W_N^{3n}
    \end{aligned}
    \end{cases},n=0,1,…,\frac N4-1
    $$

• 则得到：
  $$
  \begin{cases}
  \begin{aligned}
  X(4r)&=\sum_{n=0}^{\frac N4 -1}x_1(n)W_{\frac N4}^{nr}\
  X(4r+1)&=\sum_{n=0}^{\frac N4 -1}x_2(n)W_{\frac N4}^{nr}\
  X(4r+2)&=\sum_{n=0}^{\frac N4 -1}x_3(n)W_{\frac N4}^{nr}\
  X(4r+3)&=\sum_{n=0}^{\frac N4 -1}x_4(n)W_{\frac N4}^{nr}
  \end{aligned}
  \end{cases},r=0,1,…,\frac N4-1
  $$

• 简而言之，有：
  $$
  \begin{cases}
  \begin{aligned}
  X(4r)&=DFT[x_1(n)]\
  X(4r+1)&=DFT[x_2(n)]\
  X(4r+2)&=DFT[x_3(n)]\
  X(4r+3)&=DFT[x_4(n)]
  \end{aligned}
  \end{cases}
  $$

• 这样我们就把一个N点DFT按$k$的抽取分解为了4个$\frac N4$点DFT

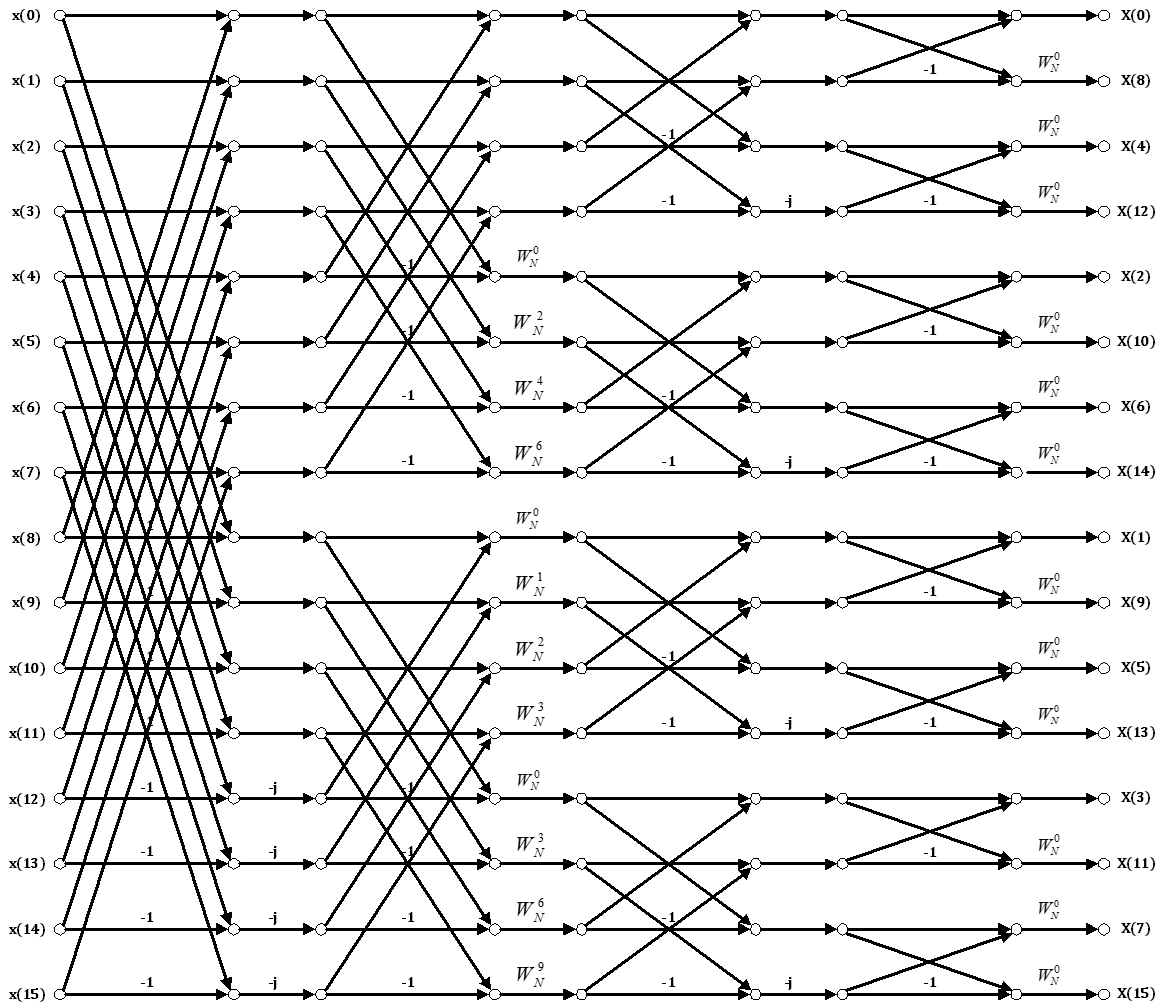
• 下面是一个按频率抽选运算的16点FFT流图：

  

---

Reference

• 快速傅里叶变换FFT_哔哩哔哩_bilibili
• 基2和基4FFT - luckylan - 博客园 (cnblogs.com)
• 基2与基4时分FFT算法浅析及其比较_基4fft-CSDN博客
• FPGA数字信号处理之基2FFT的verilog实现2哔哩哔哩_bilibili（可以参考这个视频中的代码理解，但我觉得他在进行蝶形运算时并没有进行并行处理）