本节主要介绍了浮点数与定点数的表示方法、FPGA进行数字运算的准则以及有效字长效应出现的原因
定点整数与小数的表示方法
N位负数,补码数值+原码值=$2^N$
- 例:4位补码数据:-5的补码与11($2^4-5$)的原码相同1011
- 例:4位补码数据:-7的补码与9($2^4-7$)的原码相同1011
定点小数的补码:
原则:小数点左移一位,数值为$\frac12$倍
小数的转换方法:乘以2的整数次倍M,即乘以$2^M$,转为成整数(如果是负数的话再转换为补码),再将小数点左移M位
例:十进制-1.5转换为2进制
例:十进制25.125转为2进制
浮点数
1.浮点数的表示方式
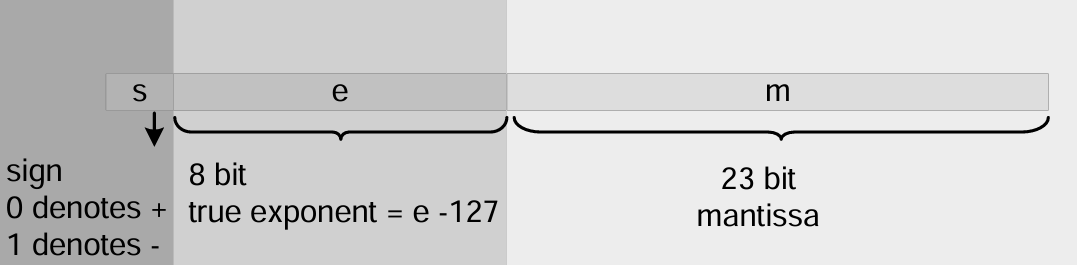
单精度 32 位浮点数的 IEEE 浮点格式:
- $s$代表符号位
- $m$代表小数部分,其隐含了一个1.,也就是它表示1~2之间的数
- $e$代表偏指数,$b$是偏差,$e-b$代表真实指数
例子:

2.浮点数的加法运算
假设有两个浮点数$0_1010_00101$和$0_1001_00101$,设偏差为7,即$b=7$
step1:通过相应移动较小指数的数字的尾数来对齐两个指数
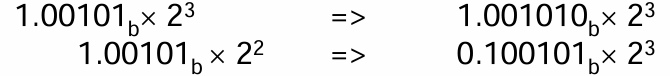
step2:尾数相加
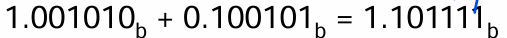
step3:位数本来只有5bit,将得到的结果最后一位截掉
step4:最后的结果是$1.10111_b\times 2^3$,它是10bit格式$0_1010_10111$
3.浮点数的乘法运算
若有两个浮点数3.5($0_1000_11000$)和5.0($0_1001_01000$),设偏差为7,即$b=7$
step1:两个数的指数相加并减去偏差
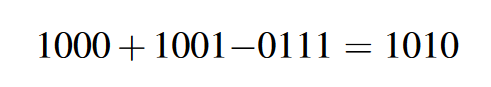
step2:添加隐含的1.,将尾数进行两个无符号乘法运算
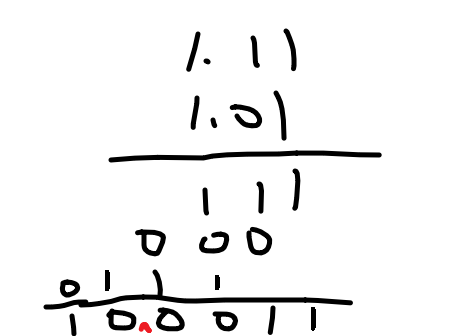
step3:整理得到的结果
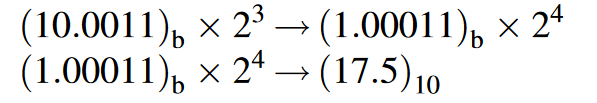
step4:将结果写成浮点数格式:

定点数
1.定点数的表示方法
定点数采用$Q_{n,m}$格式,其中$n$表示小数点左边的位数,也就是整数部分的位数,$m$表示小数点右边的位数,也就是小数点右边的位数

2.定点数的加法运算

- 。在 Q2.2 中,格式 a 是 1110,在 Q4.4 格式中,格式 b 是 0111 0110。由于 n1 小于 n2,因此扩展了 a 的符号位以将其格式从 Q2.2 更改为 Q4.2
3.定点数的乘法运算
对于乘法运算,有:
- 对于两个有符号乘法,其实是:
3.1 无符号数$\times$无符号数
无符号数的乘法不需要符号的拓展
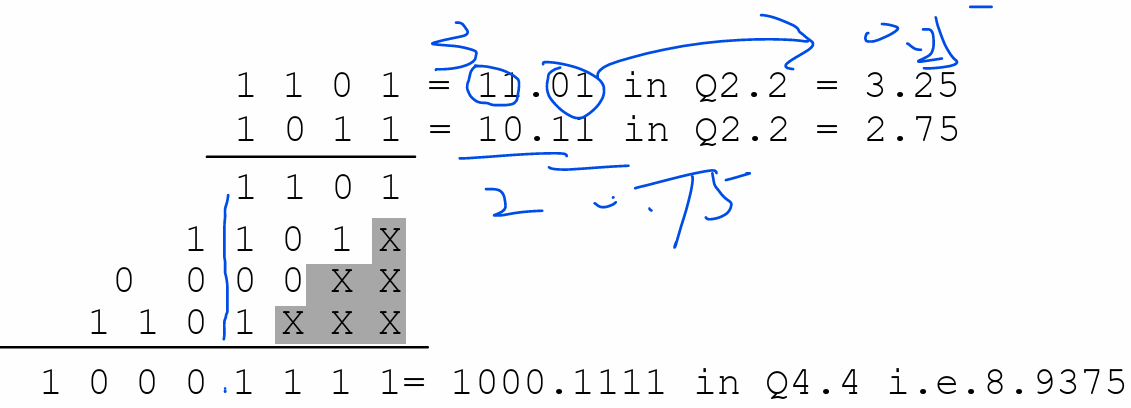
3.2 有符号数$\times$无符号数

3.3 无符号数$\times$有符号数

3.4 有符号数$\times$有符号数

并且最终的结果要左移一位,即0000_1001左移一位,得到0001_0010(个人认为其实它的最高位是冗余符号位,左移与否并不重要)
总结一下:
- 只要是负数,都用补码
- $A\times B$,A为有符号数,相乘时符号位扩展
- B为有符号数负数,最后符号位与A相乘的结果取补码
4.带截断的舍弃

AD/DA接口程序设计
无符号转成有符号:-$2^{N-1}$
有符号转成无符号:+$2^{N-1}$
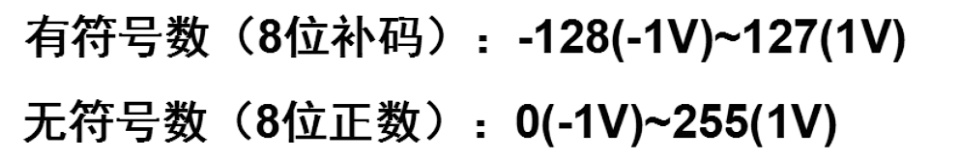
将AD采样得到的无符号数据转化成有符号数据,可供程序的其他模块使用
将有符号数据转成无符号数据送给DA
FPGA的四则运算
1.加减运算
源代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17module Data_compute(
input [3:0] d1, //操作数d1
input [3:0] d2, //操作数d2
output [3:0] unsigned_out, //无符号数加法输出
output signed [3:0] signed_out); //有符号数加法输出
//无符号数加法运算
assign unsigned_out = d1 + d2;
//有符号数加法运算
wire signed [3:0] s_d1;
wire signed [3:0] s_d2;
assign s_d1 = d1;
assign s_d2 = d2;
assign signed_out = s_d1 + s_d2;
endmodule测试代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
module tst;
// Inputs
reg [3:0] d1;
reg [3:0] d2;
// Outputs
wire [3:0] unsigned_out;
wire [3:0] signed_out;
// Instantiate the Unit Under Test (UUT)
Data_compute uut (
.d1(d1),
.d2(d2),
.unsigned_out(unsigned_out),
.signed_out(signed_out)
);
initial begin
// Initialize Inputs
d1 = 0;
d2 = 0;
// Wait 100 ns for global reset to finish
#100;
// Add stimulus here
end
reg clk=0;
always #10 clk <= ~clk;
always @(posedge clk) begin
d1 <= d1 + 1;
d2 <= d2 + 1;
end
endmodule结果如下:

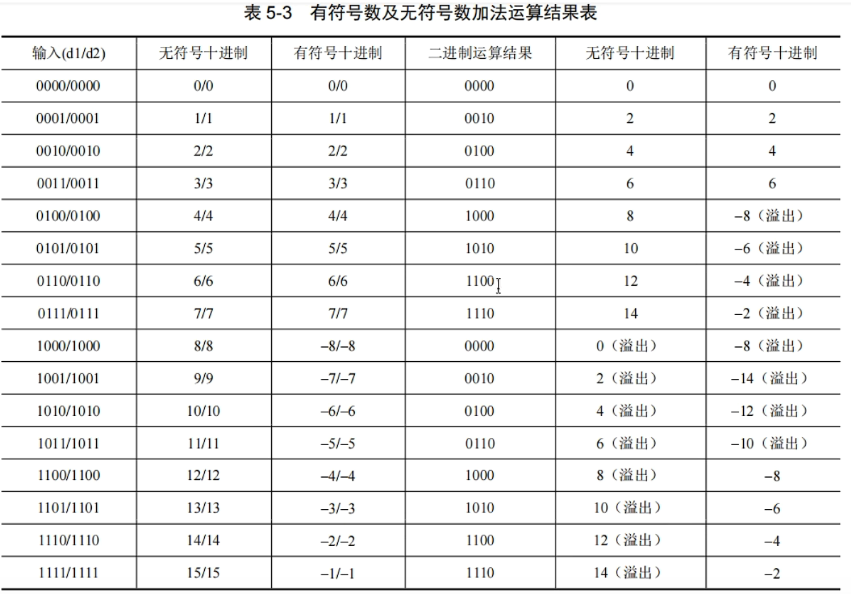
有符号数和无符号数的其实在二进制上的运算结果是一致的,只是看我们把它当作有符号数还是无符号数(对于加法和减法运算,无论有符号数还是无符号数参与运算,其结果均完全相同,因为二进制数的运算规则是完全相同的。如果将二进制数转换成十进制数,就可以看出两者的差别了)

$B$bit的二进制数,若当成无符号整数,表示的范围为$0\sim 2^B-1$,若当成有符号整数,表示的范围是$-2^{B-1}\sim 2^{B-1}-1$
- 如果二进制数的表示范围没有溢出,将运算数据均看成无符号数或有符号数,则运算结果都正确
- 两个$B$bit的二进制数进行加法和减法运算,若要运算结果不溢出,则需要$B+1$bit的数存放运算结果
- 计算多个数加减,计算的个数为$M$,则扩展位宽$N$倍,有$2^N\ge M$
- 例:两个10bit的有符号数A和B进行加法运算,则运算结果的最小值为$-2^{10}$,运算结果的最大值为$2^{10}-1$,因此需要用11bit。依次类推,如果有3~4个10 bit的有符号数进行加法运算,则需要用12bit 的数表示运算结果;如果有5~8个10bit的有符号数进行加法运算, 需要用13bit的数表示运算结果
2.乘除运算
采用移位相加实现乘法运算
- 乘法左移:

除法右移:

有效字长效应
1.乘加运算的位宽
计算所有滤波器系数绝对值之和,再计算表示该绝对值之和所需的最小无符号二进制数的位宽为n ,则滤波器输出的有效数据位为N+n
例:$2^8>1+80+80+1$,故总共需要的位宽是$10+8=18$

2.滤波器系数的字长效应
数字滤波器的系数直接决定了系统函数的零点位置、极点位置 和频率响应,因此,由于实际数字滤波器系数存在的误差,必将使数 字滤波器的零点位置和极点位置发生偏移,频率响应发生变化,从而影响数字滤波器的性能,甚至严重到使单位圆内的极点位置偏移到单位圆外,造成数字滤波器的不稳定
系数量化对数字滤波器性能的影响和字长有关,也与数字滤波器结构有关
滤波器系数的字长效应例子:
量化的方法:分子分母同时乘以一个整数,使其均为整数
MATLAB程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38b=0.05;
a=[1,1.7,0.745];
%对滤波器系数进行归一化处理
m=max(max(b),max(a));
b1=b/m;
a1=a/m;
%滤波器系数进行量化处理
Q=8;
b8=floor(b1*(2^(Q-1)-1));
a8=floor(a1*(2^(Q-1)-1));
N=2048;
xn=0:N-1;
xn=xn/N*2; %频率归一化处理
dn=[1,zeros(1,N-1)]; %产生单位抽样序列
%计算原系统的频率响应
hn=filter(b,a,dn); %计算系统单位脉冲响应
fn=10*log10(abs(fft(hn,N))); %计算系统频率响应
fn=fn-max(fn); %幅度归一化处理
%计算8比特系数量化后的系统的频率响应
hn8=filter(b8,a8,dn); %计算系统单位脉冲响应
fn8=10*log10(abs(fft(hn8,N))); %计算系统频率响应
fn8=fn8-max(fn8); %幅度归一化处理
%绘制系统的频率响应图
plot(xn(1:N/2),fn(1:N/2),'-',xn(1:N/2),fn8(1:N/2),'--');
xlabel('归一化频率(fs/2)');
ylabel('归一化幅度(dB)');
legend('原系统的频率响应','8比特量化后的频率响应');
grid on;
%计算系数的极点
s0=roots(a)
s8=roots(a8)结果如下:
从该图可明显看出系数量化后系统的频率响应与原系统的频率响应的差别,量化位数越大,频率响应越接近
观察极点位置:随着量化位数的减小, 极点值偏离原系统的极点值越来越大,对于该系统来说,当量化位数小于7位时,系统的极点已在单位圆外,不再是一个因果稳定系统
3.滤波器运算的字长效应
定点数的乘法运算存在有限字长效应,因为2个$B$bit的定点数相乘,要保留所有的有效位就需要使用$2B$bit的数,截位或舍入必定会引起有限字长效应;在浮点数运算中,乘法或加法运算均有可能引起尾数位的增加,因此也存在有限字长效应
滤波器运算的字长效应例子:
在无限精度运算的情况下,其差分方程为:
在定点数运算中,每次乘法和加法运算后都必须对尾数进行舍入或截位处理,即量化处理,而量化过程是一个非线性过程,处理后相 应的非线性差分方程变为:
MATLAB程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65x=[7/8 zeros(1,15)];
y=zeros(1,length(x)); %存放原始运算结果
B=2; %量化位数
Qy=zeros(1,length(x)); %存放量化运算结果
Qy2=zeros(1,length(x)); %存放量化运算结果
Qy4=zeros(1,length(x)); %存放量化运算结果
Qy6=zeros(1,length(x)); %存放量化运算结果
%系统系数
A=0.5;
b=[1];
a=[1,A];
%未经过量化处理的运算
for i=1:length(x);
if i==1
y(i)=x(i);
else
y(i)=-A*y(i-1)+x(i);
end
end
%经过2比特量化处理的运算
for i=1:length(x);
if i==1
Qy(i)=x(i);
Qy(i)=round(Qy(i)*(2^(B-1)))/2^(B-1);
else
Qy(i)=-A*Qy(i-1)+x(i);
Qy(i)=round(Qy(i)*(2^(B-1)))/2^(B-1);
end
end
Qy2=Qy;
B=4;
%经过4比特量化处理的运算
for i=1:length(x);
if i==1
Qy(i)=x(i);
Qy(i)=round(Qy(i)*(2^(B-1)))/2^(B-1);
else
Qy(i)=-A*Qy(i-1)+x(i);
Qy(i)=round(Qy(i)*(2^(B-1)))/2^(B-1);
end
end
Qy4=Qy;
B=6;
%经过6比特量化处理的运算
for i=1:length(x);
if i==1
Qy(i)=x(i);
Qy(i)=round(Qy(i)*(2^(B-1)))/2^(B-1);
else
Qy(i)=-A*Qy(i-1)+x(i);
Qy(i)=round(Qy(i)*(2^(B-1)))/2^(B-1);
end
end
Qy6=Qy;
%绘图显示不同量化位宽的滤波结果
xa=0:1:length(x)-1;
plot(xa,y,'-',xa,Qy2,'--',xa,Qy4,'O',xa,Qy6,'+');
legend('原系统运算结果','2bit量化运算结果','4bit量化运算结果','6bit量化运算结果')
xlabel('运算次数');ylabel('滤波结果');- 结果如下:
从图中可以看出,当采用无限精度进行运算时,输出响应逐渐趋近于0;经过量化处理后,输出响应在几次运算后在固定值处振荡,量化位数越少,振荡幅度就越大
