本节主要介绍了数字信号处理中的一些频域上的处理,包括低通带通采样定理,DTFT、DFS、DFT。
带通采样定理
采样是频谱的左右搬移(以采样频率$f_s$左右搬移)
那么对于一个$f_L\sim f_H$的窄带信号采样,有:
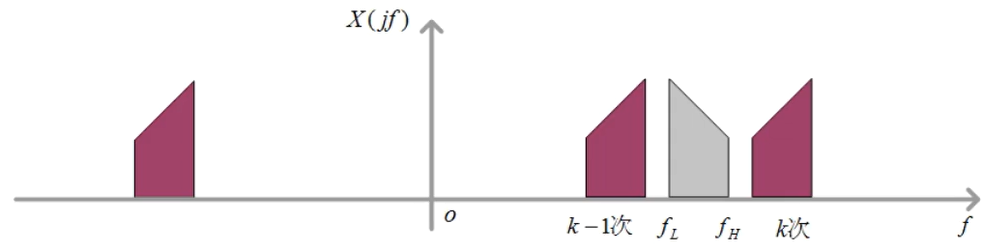
只有当频谱不发生交叠时,才能完全恢复出时域信号
那么需满足如下条件:
整合上述两式可得到:
用一个matlab示例程序来演示带通采样频率的取值
1
2
3
4
5
6
7
8
9clc; %清屏
clear all; %清变量
fL=60;
fH=69;
B=fH-fL;
k=1:(fH/B);
fs_min=2*fH./k
fs_max=2*fL./(k-1)结果如下:

奈奎斯特采样定理
采样频率$f_s\ge 2f_H$(信号最高频率为$f_H$)
用一个matlab程序示例来理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17clc; %清屏
clear all; %清变量
N=70; %数据长度
fs=64000; %采样频率
f0=67000;
f1=3000;
t=0:(N-1);
t=t/fs; %时间序列
s0=sin(2*pi*f0*t);
s1=sin(2*pi*f1*t);
%绘图
subplot(211);plot(t,s0); title('f0=67kHz');
subplot(212);plot(t,s1); title('f1=3kHz');结果如下:
可见采样后67KHz的频率和3KHz的频率的时域信号一样
其原因在于,采样是频谱以$f_s$的线性搬移,搬移后的频率会通过一个低通滤波器,也就是只留下频谱在$\pm \frac{f_s}2$之间的频率,即:
所以67KHz会有一个搬移到3KHz(67KHz-64KHz),3KHz在32KHz内,故采样滤波后会输出一个3KHz的正弦波
时域离散傅里叶变换
离散时间傅里叶变换的公式:
$x(e^{jw})$是角频率以$2\pi$为周期的函数
理想低通滤波器的iDTFT
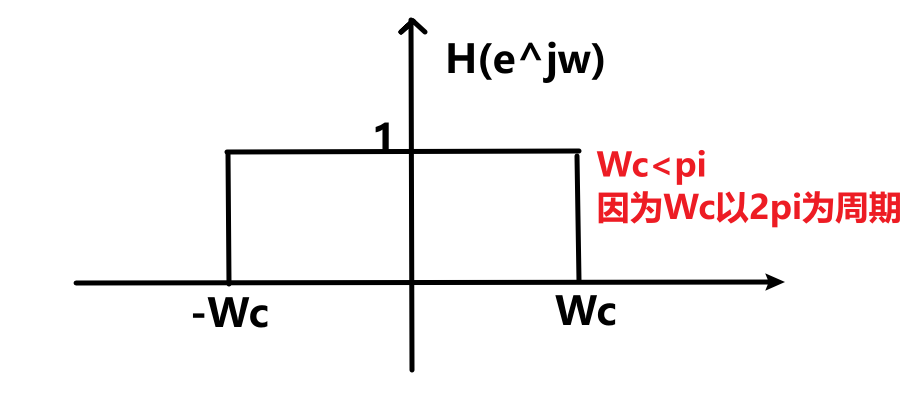
逆变换的公式推导:
由Matlab可以画出理想低通滤波器的时域波形
1
2
3
4
5
6
7
8
9clc; %清屏
clear all; %清变量
wc=0.5;
n=-200:200;
hn=sin(wc*n)./(pi*n);
stem(n,hn)
xlabel('n');
ylabel('hn');结果如下:
时域离散傅里叶级数
- 离散傅里叶级数的公式:
- 更详细的解释见我的另一篇文章:信号处理中的小知识点
离散傅里叶变换
离散傅里叶变换的公式:
DFT一定是关于$\frac N2$共轭对称的,也就是$x(k_0)=x(N-k_0)$共轭
1.MATLAB辅助理解DFT
通过Matlab来理解DFT的计算过程:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21clc; %清屏
clear all; %清变量
N=16; %矩形序列的周期
L=4; %矩形序列的长度
rn=ones(1,L); %矩形的长度
xn=[rn,zeros(1,N-L)];
n=0:N-1;
xk=fft(rn,N); %离散谱
w=0:0.1:2*pi;
xw=(1-exp(-j*w*L))./(1-exp(-j*w)); %连续谱
subplot(311)
stem(n,xn);title('x(n)');grid on;
subplot(312);
stem(n,abs(xk));title('X(K)'); grid on;
subplot(313)
plot(w,abs(xw));title('X(jw)');grid on;结果如下:
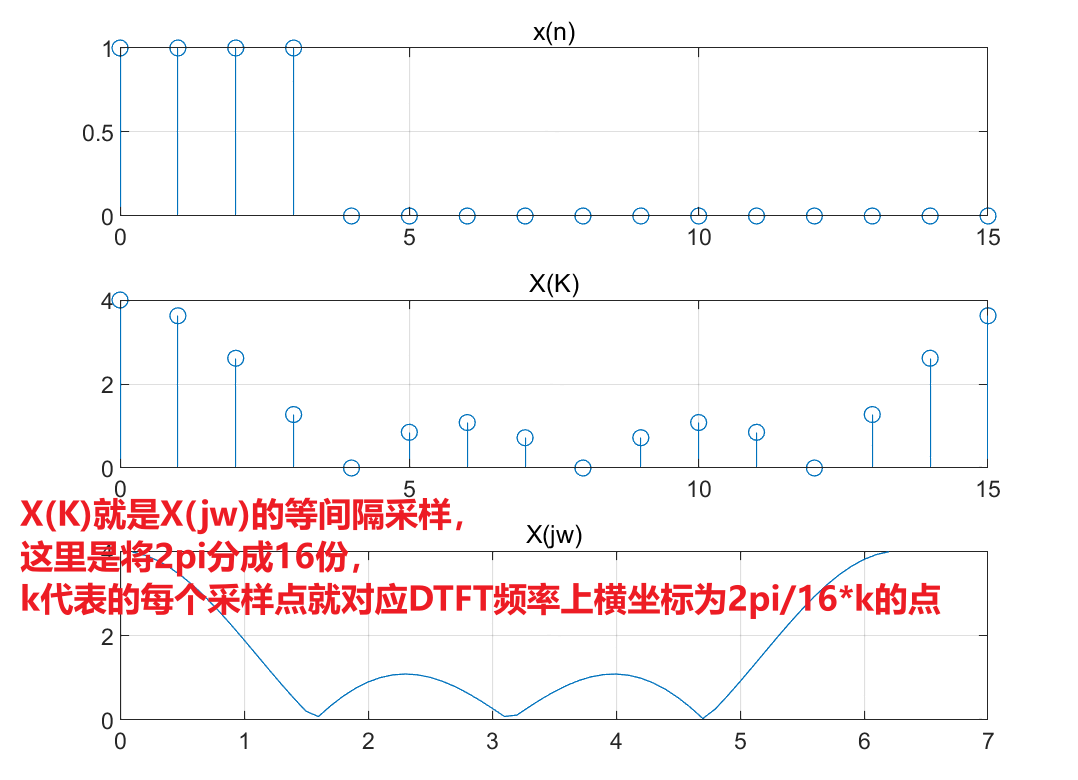
借助matlab讨论N点不同时对幅频特性的影响
不同序列信号,参与DFT计算的N不同时,DFT可以一样,也可以不一样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27clc;clear all; %清屏清变量
n1=0:3; n2=4:7;
n=[n1,n2];
x2n1=n1+1;
x2n2=8-n2;
x2n=[x2n1,x2n2];
x3n1=4-n1;
x3n2=n2-3;
x3n=[x3n1,x3n2];
subplot(321);stem(x2n);title('xn2');
subplot(322);stem(x3n);title('xn3');
subplot(323);stem(abs(fft(x2n,8)));title('DFT(x2n,8)');
subplot(324);stem(abs(fft(x3n,8)));title('DFT(x3n,8)');
subplot(325);stem(abs(fft(x2n,16)));title('DFT(x2n,16)');
subplot(326);stem(abs(fft(x3n,16)));title('DFT(x3n,16)');
figure(2)
subplot(221);stem([x2n x2n x2n x2n]);title('xn2\_8\_repeat4');
subplot(222);stem([x3n x3n x3n x3n]);title('xn3\_8\_repeat4');
x2n=[x2n,zeros(1,8)];
x3n=[x3n,zeros(1,8)];
subplot(223);stem([x2n x2n x2n x2n]);title('xn2\_16\_repeat4');
subplot(224);stem([x3n x3n x3n x3n]);title('xn3\_16\_repeat4');- 结果如下:
观察到,输入有限序列xn2和xn3不同,但当做8点ffts时,二者结果相同,做16点fft时,二者结果不同
究其原因,首先画出xn2和xn3分别进行8和16点周期延拓的序列图像
从图中可以看到,进行8点周期延拓后,xn2和xn3是相同的周期信号,只是相位不同,但并不会影响DFT的幅频特性
进行16点周期延拓后,xn2和xn3显然不是同一个周期信号,故DFT的结果也会不一致
从上述分析得出结论,DFT是将M个有限序列进行N点(N>M时补零)进行周期延拓,然后选取一个周期内的序列,进行DFT计算
对同一序列,进行不同N的DFT计算,结果也会不同
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18clc;clear all; %清屏清变量
fs=100; %采样频率
f=10; %信号频率
t=0:1/fs:10; %时间序列
x=sin(2*pi*f*t); %正弦信号
%绘制幅频响应
figure(1);
subplot(211);stem(abs(fft(x,40)));
subplot(212);stem(abs(fft(x,45)));
figure(2)
x40=[x(1:40),x(1:40),x(1:40),x(1:40)];
x45=[x(1:45),x(1:45),x(1:45),x(1:45)];
subplot(211);plot(x40); title('x40');
subplot(212);plot(x45); title('x45');- 结果如下:
从结果图中观察到对sin函数进行40点DFT和45点DFT是不一样
究其原因,首先可以画出在时域上分别采样40点和45点的时域波形
观察上图,因为在时域上取45点序列进行周期延拓后形成的波形,并不是一个正常的正弦波,故最后的DFT结果当然跟理想的sin频谱不一样,其实这里就是出现频谱泄露的原因,也就是后面为什么会有窗函数这个玩意
关于为什么40点是正常的正弦波而45点不是正常的正弦波的解释:
- 信号频率为10Hz,采样频率为100Hz,也就是一个周期采10个点,40个点也就是采了4个周期
- 而45并不是10的倍数,采样了4个多一点的周期,所以周期延拓后并不是一个正常的正弦波
借sin函数讨论不同N对幅频特性中幅度的影响
1
2
3
4
5
6
7
8
9
10
11
12
13
14clc;clear all; %清屏清变量
fs=100; %采样频率
f=10; %信号频率
t=0:1/fs:10; %时间序列
x=sin(2*pi*f*t); %正弦信号
%绘制幅频响应
figure(1);
subplot(411);stem(abs(fft(x,20)));title('DFT\_x20');
subplot(412);stem(abs(fft(x,80)));title('DFT\_x80');
subplot(413);stem(abs(fft(x,160)));title('DFT\_x160');
subplot(414);stem(abs(fft(x,1000)));title('DFT\_x1000');结果如下:
这张图完美诠释了,N点double,FFT幅度会double
但前提是N<M,且N需要是$\frac{f_s}{f_0}$的倍数
2.循环卷积原理
公式如下:
循环卷积长度:若$x(n):L,h(n):M$,那么循环长度$N$为:
- 是对$L$或者$M$的长度补零,补到比$L+M-1$长,那么循环卷积和线性卷积相等
当循环卷积长度$\ge$线性卷积长度$(L+M-1)$时,二者计算得到的结果相等
循环卷积的计算示例:
| | | | $a(n)$ | 1 | 2 | 3 | 4 | | | | |
| ——————————— | —— | —— | ——— | —— | —— | —— | —— | —— | —— | —— | ————- |
| $b(n)$翻转后的周期延拓 | 0 | 7 | 6 | 5 | 0 | 7 | 6 | 5 | 0 | 7 | $c(0)=50$ |
| 翻转延拓后向右移动1 | 5 | 0 | 7 | 6 | 5 | 0 | 7 | 6 | 5 | 0 | $c(1)=44$ |
| 翻转延拓后向右移动2 | 6 | 5 | 0 | 7 | 6 | 5 | 0 | 7 | 6 | 5 | $c(2)=34$ |
| 翻转延拓后向右移动3 | 7 | 6 | 5 | 0 | 7 | 6 | 5 | 0 | 7 | 6 | $c(3)=52$ |MATLAB的验证
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19clc;
an=[1 2 3 4];
bn=[5 6 7];
%4点DFT验证循环卷积的计算
an_fft_4=fft(an,4);
bn_fft_4=fft(bn,4);
cn_circle_4=ifft((an_fft_4.*bn_fft_4),4)
%6点DFT验证循环卷积与线性卷积相等
an_fft_6=fft(an,6);
bn_fft_6=fft(bn,6);
cn_linear=conv(an,bn)
cn_circle_6=ifft((an_fft_6.*bn_fft_6),6)
%大于6点DFT时循环卷积的结果
an_fft_8=fft(an,8);
bn_fft_8=fft(bn,8);
cn_circle_8=ifft((an_fft_8.*bn_fft_8),8)- 结果如下:

