本节以静态时序分析为切入口,重点理解建立时间、保持时间以及裕量分析。
静态时序分析
静态时序分析(static timing analysis,STA)是遍历电路存在的所有时序路径,根据给定工作条件(PVT:制造工艺Process、工作电压Voltage、温度Temperature)下的时序库.lib文件计算信号在这些路径上的传播延时,检查信号的建立和保持时间是否满足约束要求,根据最大路径延时和最小路径延时找出违背时序约束的错误
静态时序分析的优点:
不需要给输入激励;
几乎能找到所有的关键路径(critical path);
运行速度快
静态时序分析的缺点:
只适用同步电路;
无法验证电路的功能;
- 需要比较贵的工具支持;
- 对于新工艺可能还需要建立一套特征库,建库的代价可能要几百万。
静态时序分析的工具:
- Synopsys的prime time,
- Cadence的Encounter Timing System等
寄存器延迟
- 建立时间$t_{setup}$:数据D需要提前clk上升沿多长时间到来,数据的采集才不会出错
- 保持时间$t_{hold}$:时钟上升沿到来后,数据D还需要维持多长时间不变,才不会影响输出Q
- 传输延时$t_{cq}$:时钟上升沿到来后多久,数据才能传输到Q端
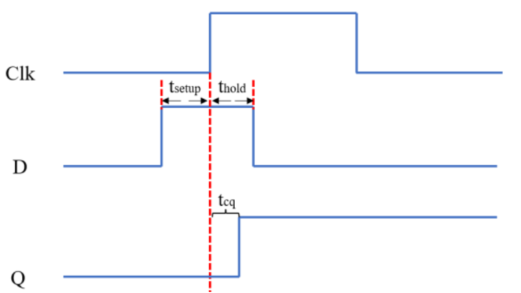
建立、保持时间裕量分析
时钟无延迟的情况下:
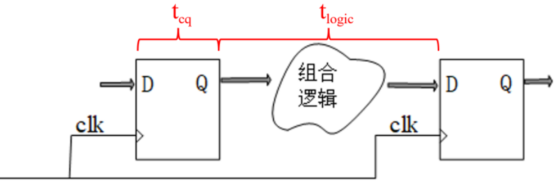
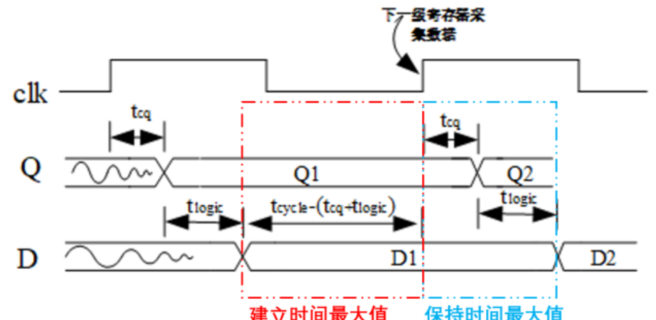
- 建立时间:
- 建立时间最大值=$t_{cycle}-(t_{cq}+t_{logic})$
- 建立时间裕量=$t_{cycle}-(t_{cq}+t_{logic})-t_{setup}$
- 保持时间:
- 保持时间最大值=$t_{cq}+t_{logic}$
- 保持时间裕量=$t_{cq}+t_{logic}-t_{hold}$
- 建立时间:
时钟有延时的情况下:
时钟正向延迟的情况下:
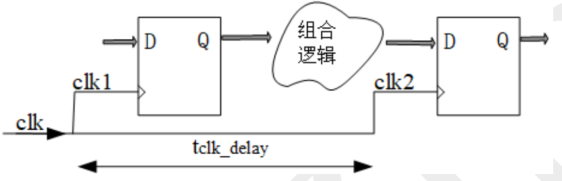
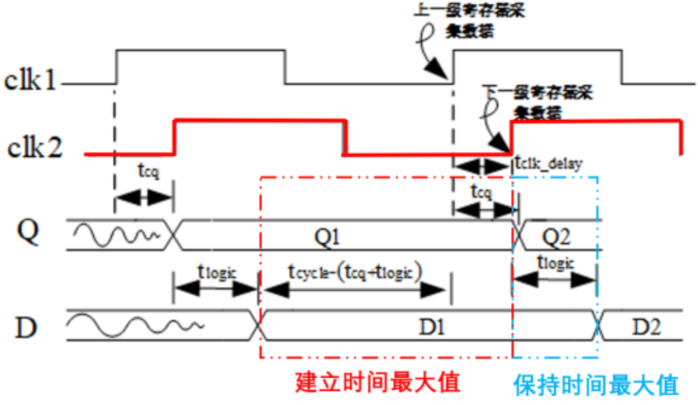
- 建立时间:
- 建立时间最大值=$t_{cycle}-(t_{cq}+t_{logic})+t_{clk_delay}$
- 建立时间裕量=$t_{cycle}-(t_{cq}+t_{logic})-t_{setup}+t_{clk_delay}$
- 保持时间:
- 保持时间最大值=$t_{cq}+t_{logic}-t_{clk_delay}$
- 保持时间裕量=$t_{cq}+t_{logic}-t_{hold}-t_{clk_delay}$
- 时钟存在抖动:
- 建立时间:
- 建立时间最大值=$t_{cycle}-(t_{cq}+t_{logic})+t_{clk_delay}-t_{jitter}$
- 建立时间裕量=$t_{cycle}-(t_{cq}+t_{logic})-t_{setup}+t_{clk_delay}-t_{jitter}$
- 保持时间:
- 保持时间最大值=$t_{cq}+t_{logic}-t_{clk_delay}-t_{jitter}$
- 保持时间裕量=$t_{cq}+t_{logic}-t_{hold}-t_{clk_delay}-t_{jitter}$
- 建立时间:
- 建立时间:
时钟反向延迟的情况下:
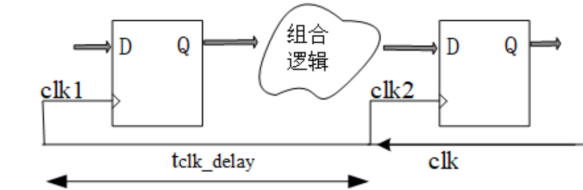
- 建立时间:
- 建立时间最大值=$t_{cycle}-(t_{cq}+t_{logic})-t_{clk_delay}$
- 建立时间裕量=$t_{cycle}-(t_{cq}+t_{logic})-t_{setup}-t_{clk_delay}$
- 保持时间:
- 保持时间最大值=$t_{cq}+t_{logic}+t_{clk_delay}$
- 保持时间裕量=$t_{cq}+t_{logic}-t_{hold}+t_{clk_delay}$
- 建立时间:
基本同步时钟约束路径
1.内部寄存器到内部寄存器
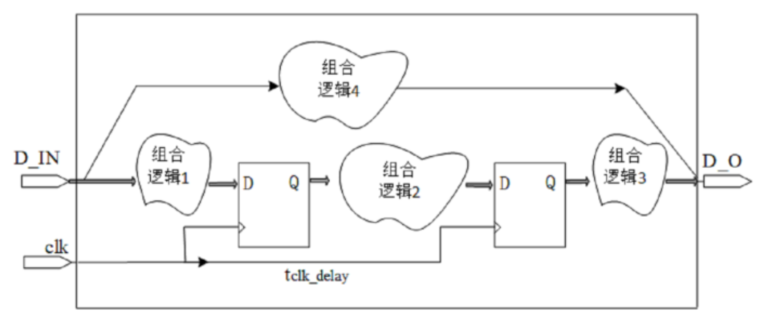
- 建立时间裕量:$t_{setup_slack}=t_{cycle}-(t_{cq}+t_{logic})-t_{setup}+t_{clk_delay}-t_{jitter}>0$
- 保持时间裕量:$t_{hold_slack}=t_{cq}+t_{logic}-t_{hold}-t_{clk_delay}-t_{jitter}>0$
- 手动设置clk时钟周期,如:
create_clock-period 10 [get_ports clk] - EDA会根据我们给出的$t_{cycle}$,去计算建立保持时间裕量
- EDA会优化寄存器到寄存器之间的组合逻辑2的延时$t_{logic}$和$t_{clk_delay}$,以满足建立保持时间裕量要求
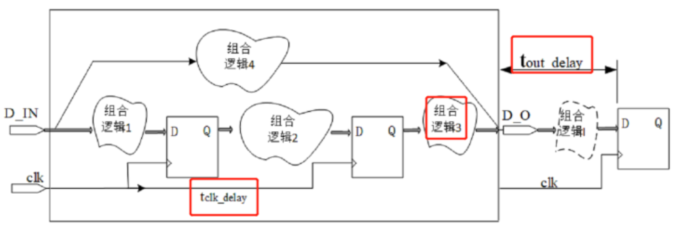
2.输入端口到内部寄存器
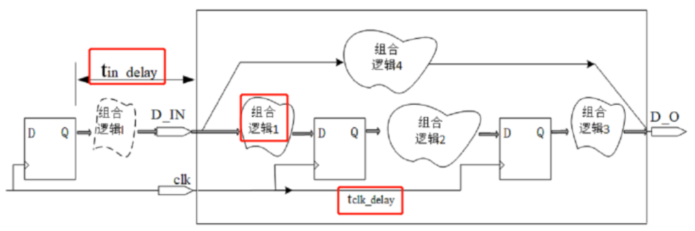
建立时间裕量:$t_{setup_slack}=t_{cycle}-t_{logic1}-t_{in_delay}-t_{setup}+t_{clk_delay}-t_{jitter}>0$
保持时间裕量:$t_{hold_slack}=t_{logic1} + t_{in_delay}-t_{hold}-t_{clk_delay}-t_{jitter}>0$
需输入$t_{cycle},t_{in_delay}$(其中$t_{in_delay}$等于上一级电路寄存器的输出延迟($t_{cq}$)加上一级组合逻辑的延时)
EDA会优化组合逻辑1的延时$t_{logic1}$和$t_{clk_delay}$
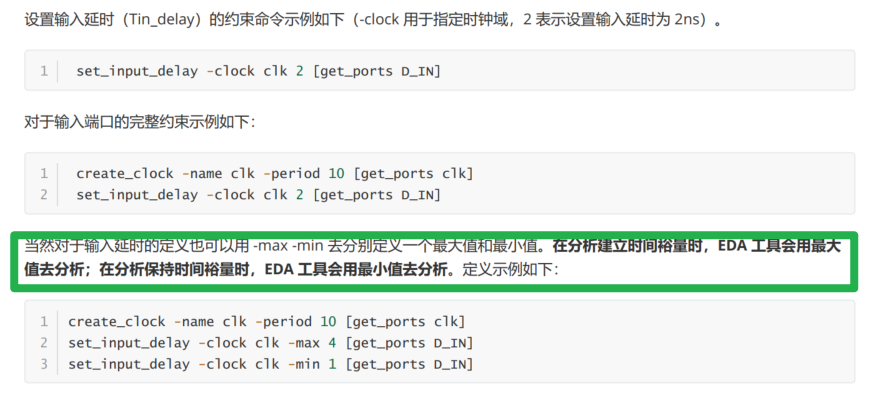
3.内部寄存器到输出端口
- 建立时间裕量:$t_{setup_slack}=t_{cycle}-t_{logic3}-t_{out_delay}-t_{setup}+t_{clk_delay}-t_{jitter}>0$
- 保持时间裕量:$t_{hold_slack}=t_{logic3} + t_{out_delay}-t_{hold}-t_{clk_delay}-t_{jitter}>0$
- 需输入$t_{cycle},t_{out_delay}$
4.输入端口到输出端口
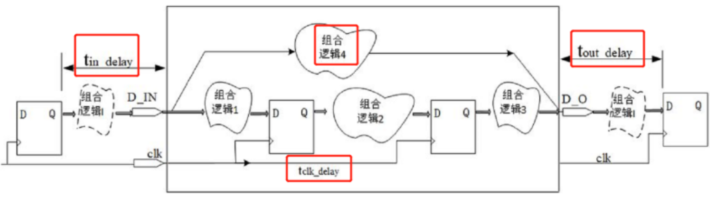
建立时间裕量:$t_{setup_slack}=t_{cycle}-t_{logic4}-t_{in_delay}-t_{out_delay}-t_{setup}+t_{clk_delay}-t_{jitter}>0$
保持时间裕量:$t_{hold_slack}=t_{logic4} + t_{out_delay}+t_{in_delay}-t_{hold}-t_{clk_delay}-t_{jitter}>0$
需输入$t_{cycle},t_{in_delay},t_{out_delay}$(其中$t_{out_delay}$的含义是输出信号在后级模块中需要在时钟沿之前提前多长时间准备好)
最高时钟频率计算
只有建立时间裕量与系统工作时钟周期有关,当建立时间裕量为0,系统时钟周期会最小,对应频率最高,即:
那么,时钟周期的最小值为:
因此,系统工作时钟频率最大为:
时序违例的优化方法概述
- 建立时间违例:
- 前端设计方案:
- 关键路径上的逻辑并行:串行—>并行
- 卡诺图化简
- 插入寄存器,形成流水线设计
- 后端设计方案:
- 调整关键路径时钟的$t_{clk_delay}$,一般针对小范围的违例
- 采用多阈值单元,关键路径采用阈值小的单元
- 采用面积更小的门级单元
- 其他方案:
- 降低时钟频率,增大时钟周期(但频率不能变动太大)
- 替换先进的工艺
- 提高工作电压,减小信号延迟
- 前端设计方案:
- 保持时间违例:
- 在组合逻辑中插入延时buffer,使得$t_{logic}$变大
- 调小正向时钟延时$t_{clk_delay}$
- 提高温度,降低电压,增大信号延迟
- 降低时钟频率无法解决保持时间为例的问题,毕竟保持时间公式里没有$t_{cycle}$,与$t_{cycle}$无关
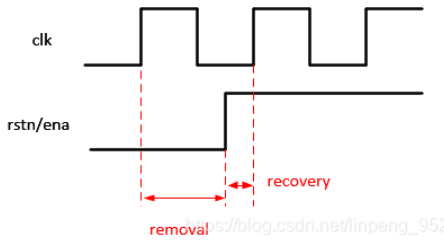
恢复与去除时间
恢复时间(Recovery time):异步信号在时钟来临之前shu’ru有效稳定不变的时间
去除时间(Removal time):异步信号在时钟边沿之后输入信号有效且稳定不变的时间
Reference
- 新新新手Icer练习(六):静态时序分析,深入了解建立时间、保持时间及其裕量分析_哔哩哔哩_bilibili(可以说,我这篇笔记全文抄袭该视频的,只是自己打了一遍公式,加深了一下印象,记录一下。不得不感叹一句,这位博主讲得东西简单明了,优秀)
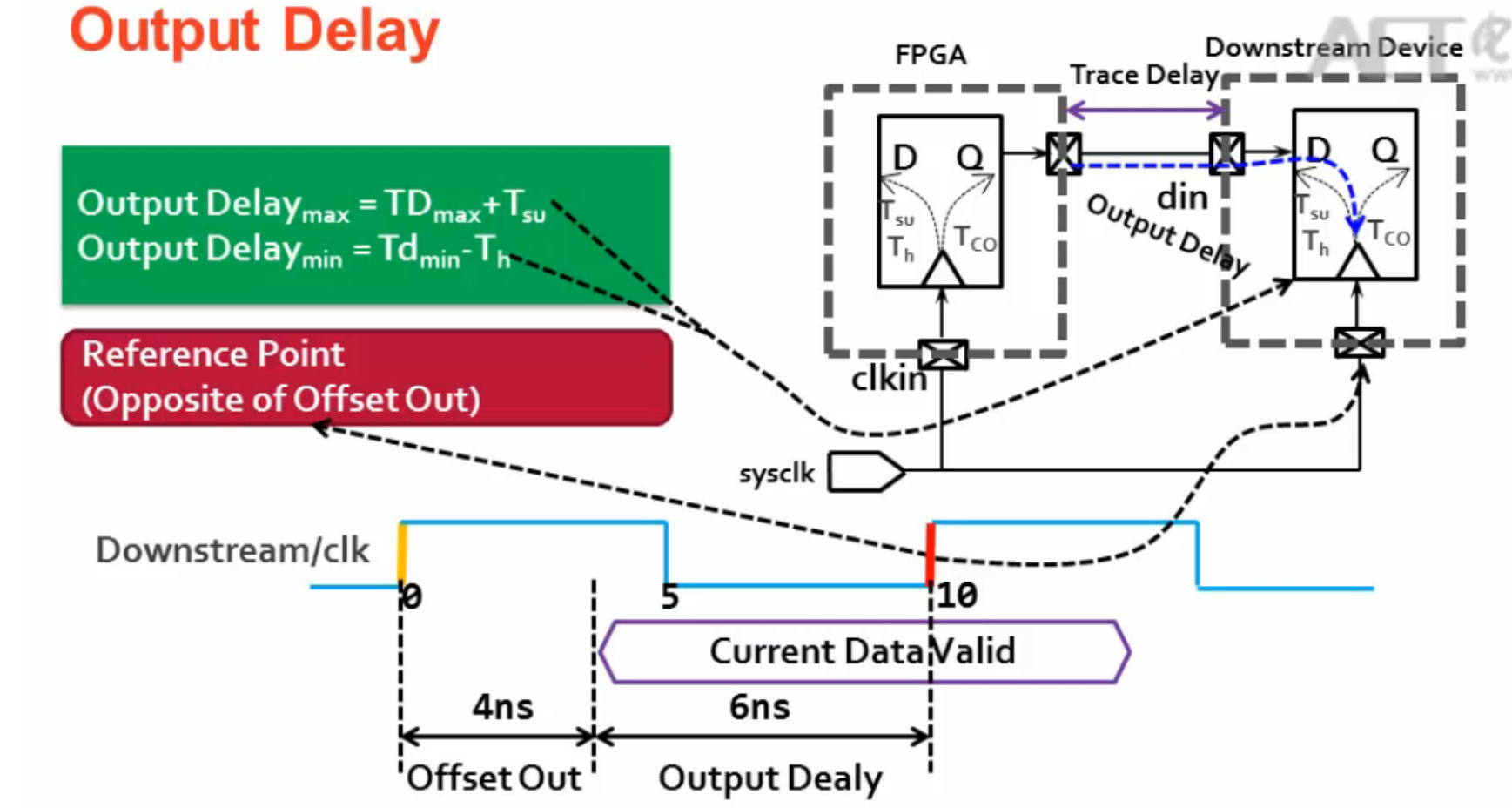
- 输入延时(Input Delay)与输出延时(Output Delay)-CSDN博客
