本节主要介绍了FPGA图像处理中常用的图像缩放算法,包括最近邻插值算法、双线性邻插值算法、双三次邻插值算法,以及它们的MATLAB与FPGA实现。
最近邻插值算法
最近邻插值算法是一种简单的插值算法,容易实现,但该算法会在新图像中产生明显的锯齿边缘和马赛克现象。
计算点$P(x,y)$与邻近4个点$A(x_1,y_1)$、$B(x_2,y_2)$、$C(x_3,y_3)$、$D(x_4,y_4)$的距离,并将与点$P(x,y)$最近的整数坐标点$A(x_1,y_1)$的灰度值作为点$P(x,y)$的灰度近似值
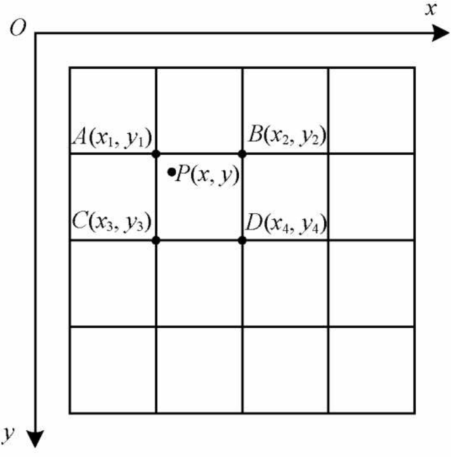
在实际matlab实现中:
- 首先,计算原始图像与放大后的图像在水平方向和垂直方向的比率(即步进)$x_ratio$和$y_ratio$
- 其次,根据比率$x_ratio$和$y_ratio$,计算放大后的图像坐标$(i,j)$到原始图像坐标$(x,y)$的映射
- 最后,将原始图像中的灰度值$img1(y,x)$作为放大后图像的近似灰度值$img2(i,j)$
1
2
3
4
5
6
7
8
9
10
11
12function [img2] = Nearest_Interpolation(img1,h1,w1,h2,w2)
x_ratio = w1/w2;
y_ratio = h1/h2;
for i = 1 : h2
y = 1+round((i-1)*y_ratio);
for j = 1 : w2
x = 1+round((j-1)*x_ratio);
img2(i,j) = img1(y,x);
end
end
1.最近邻插值的MATLAB实现
为适配后续FPGA对最近邻插值算法的实现,需将浮点运算转为定点运算,即将水平方向比率$x_ratio$和垂直方向比率$y_ratio$的精度定标为16位小数
matlab代码:
1
2
3
4
5
6
7
8
9
10
11
12function [img2] = Nearest_Interpolation_Int(img1,h1,w1,h2,w2)
x_ratio = floor(w1/w2*2^16)/2^16;
y_ratio = floor(h1/h2*2^16)/2^16;
for i = 1 : h2
y = 1+round((i-1)*y_ratio);
for j = 1 : w2
x = 1+round((j-1)*x_ratio);
img2(i,j) = img1(y,x);
end
end
2.最近邻插值的FPGA实现
根据matlab仿真,仔细观察$y$(原图的高)与$i$(放大图的高)的对应关系会发现:
- 如果放大图第$i$行对应原图的第$y$行,那么放大图中的第$i+1$行要么对应原图的第$y$行,要么对应原图的第$y+1$行,那么计算原图中的第$i$行时,需要缓存$y$与$y+1$行后才可以开始正式缩放
- 而究竟是取$y$还是$y+1$行的数取决于步长$y_ratio$,即$i+1 \leftarrow round(y(未经过四舍五入)+y_ratio)$
最近邻插值放大算法的实现分解为以下几步:
对原始图像进行行缓存:为了简化BRAM地址的计算,BRAM为每行像素开辟了1024个地址空间。从另一个角度来说,BRAM可用于缓存行像素数量在1024以内的图像。最后将BRAM的深度定义为4096,即BRAM最多可以缓存4行的像素。另外,因为图像像素的位宽为8bit,所以将BRAM的数据位宽定义为8bit。
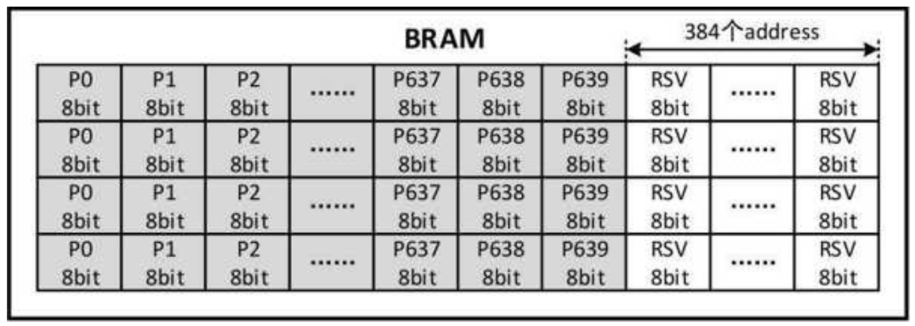
将原始图像存入BRAM之前,需要产生相应的BRAM地址。根据原始图像的场信号$per_img_vsync$和行信号$per_img_href$,对原始图像进行列统计$img_hs_cnt\in[0,C_SRC_IMG_WIDTH - 1]$和行统计$img_vs_cnt\in[0,C_SRC_IMG_HEIGHT - 1]$,其中,$C_SRC_IMG_WIDTH$和$C_SRC_IMG_HEIGHT$分别表示原始图像的宽度和高度
- 其中,$img_hs_cnt$用于产生行内像素的地址;$img_vs_cnt[1:0]$用于产生不同行的基地址(绝妙啊)
1
2
3
4always @(posedge clk_in1)
begin
bram_a_waddr <= {img_vs_cnt[1:0],10'b0} + img_hs_cnt;
end当每行像素缓存到BRAM后,将行统计$img_vs_cnt$作为标签存入异步FIFO中。后续进行最近邻插值放大时,会根据该标签判断BRAM是否已经缓存了插值所需要的两行像素
1
2
3
4
5
6
7S_Y_LOAD :
begin
if((y_dec[26:16] + 1'b1 <= fifo_rdata)||(y_cnt == C_DST_IMG_HEIGHT - 1'b1))
state <= S_BRAM_ADDR;
else
state <= S_RD_FIFO;
end在进行最近邻插值放大之前,需要计算原始图像与目标图像在水平方向和垂直方向上的比率(即目标图像映射到原始图像的坐标步进)$C_X_RATIO$和$C_Y_RATIO$。已知原始图像的分辨率为$640\times 480$、目标图像的分辨率为$1024\times 768$,且要求将比率定标为16位小数,故$C_X_RATIO$和$C_Y_RATIO$的计算结果为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26always @(posedge clk_in2)
begin
if(rst_n == 1'b0)
y_dec <= 27'b0;
else
begin
if((state == S_IDLE)&&(fifo_empty == 1'b0)&&(fifo_rdata == 11'b0))
y_dec <= 27'b0;
else if(state == S_Y_INC)
y_dec <= y_dec + C_Y_RATIO;
else
y_dec <= y_dec;
end
end
always @(posedge clk_in2)
begin
if(state == S_BRAM_ADDR)
x_dec <= x_dec + C_X_RATIO;
else
x_dec <= 27'b0;
end
always @(posedge clk_in2)
begin
x_int_c1 <= x_dec[26:16] + x_dec[15];
y_int_c1 <= y_dec[26:16] + y_dec[15];
end最后就用一个状态机来控制BRAM的读取

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51always @(posedge clk_in2)
begin
if(rst_n == 1'b0)
state <= S_IDLE;
else
begin
case(state)
S_IDLE :
begin
if(fifo_empty == 1'b0)
begin
if((fifo_rdata != 11'b0)&&(y_cnt == C_DST_IMG_HEIGHT))
state <= S_RD_FIFO;
else
state <= S_Y_LOAD;
end
else
state <= S_IDLE;
end
S_Y_LOAD :
begin
if((y_dec[26:16] + 1'b1 <= fifo_rdata)||(y_cnt == C_DST_IMG_HEIGHT - 1'b1))
state <= S_BRAM_ADDR;
else
state <= S_RD_FIFO;
end
S_BRAM_ADDR :
begin
if(x_cnt == C_DST_IMG_WIDTH - 1'b1)
state <= S_Y_INC;
else
state <= S_BRAM_ADDR;
end
S_Y_INC :
begin
if(y_cnt == C_DST_IMG_HEIGHT - 1'b1)
state <= S_RD_FIFO;
else
state <= S_Y_LOAD;
end
S_RD_FIFO :
begin
state <= S_IDLE;
end
default :
begin
state <= S_IDLE;
end
endcase
end
end将最近邻像素的坐标$(y_int_c1,x_int_c1)$转为BRAM的读地址
1
2
3
4always @(posedge clk_in2)
begin
bram_b_raddr <= {y_int_c1[1:0],10'b0} + x_int_c1;
end
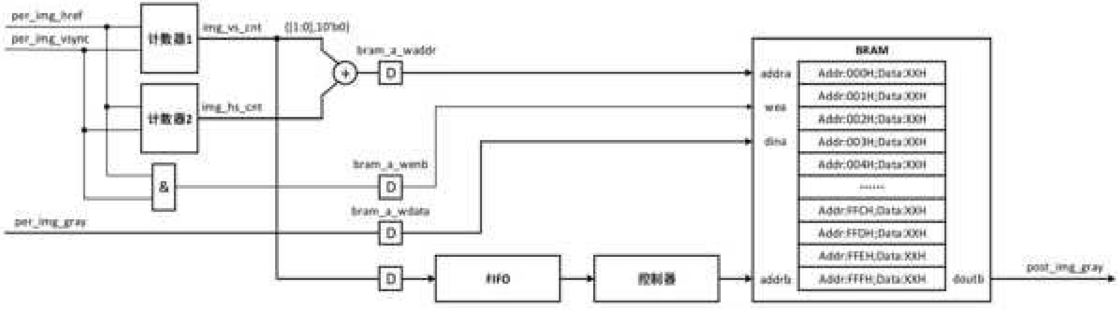
最后有一点需要说明的是, 原始图像的时钟频率F1与目标图像的时钟频率F2必须满足以下关系,才能确保实时处理, 否则将导致BRAM中的旧数据被新数据覆盖, 以及FIFO溢出等错误或异常情况
仿真结果:

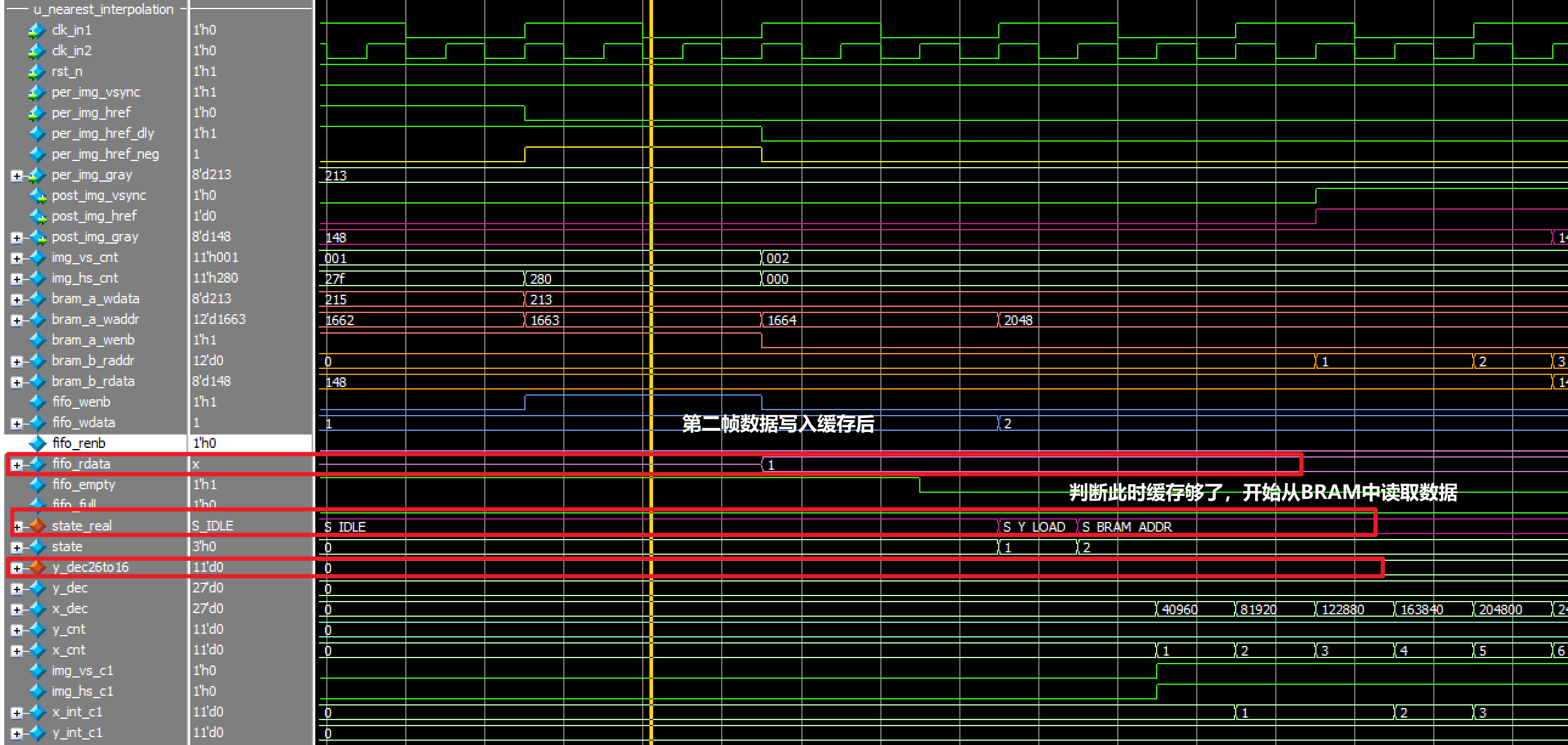
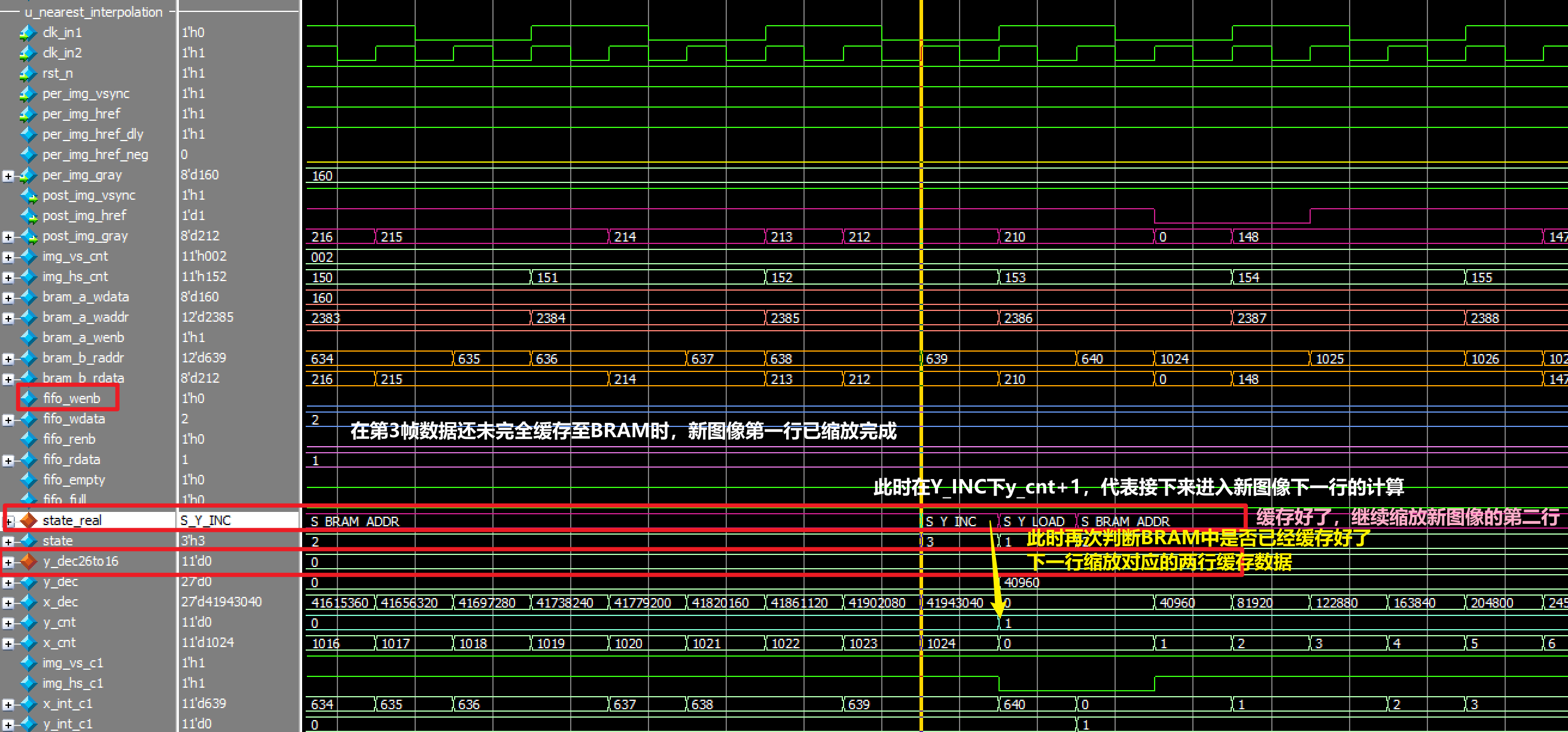
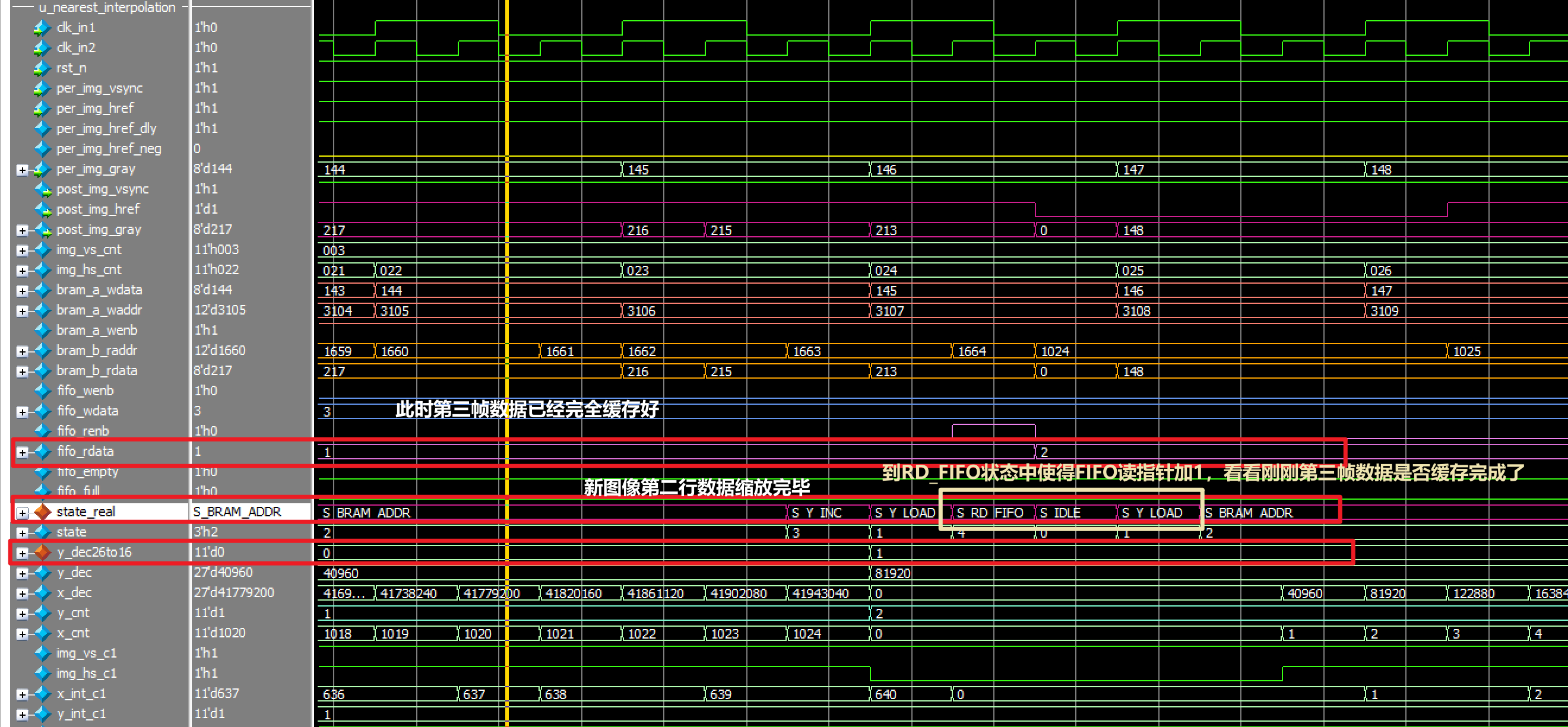
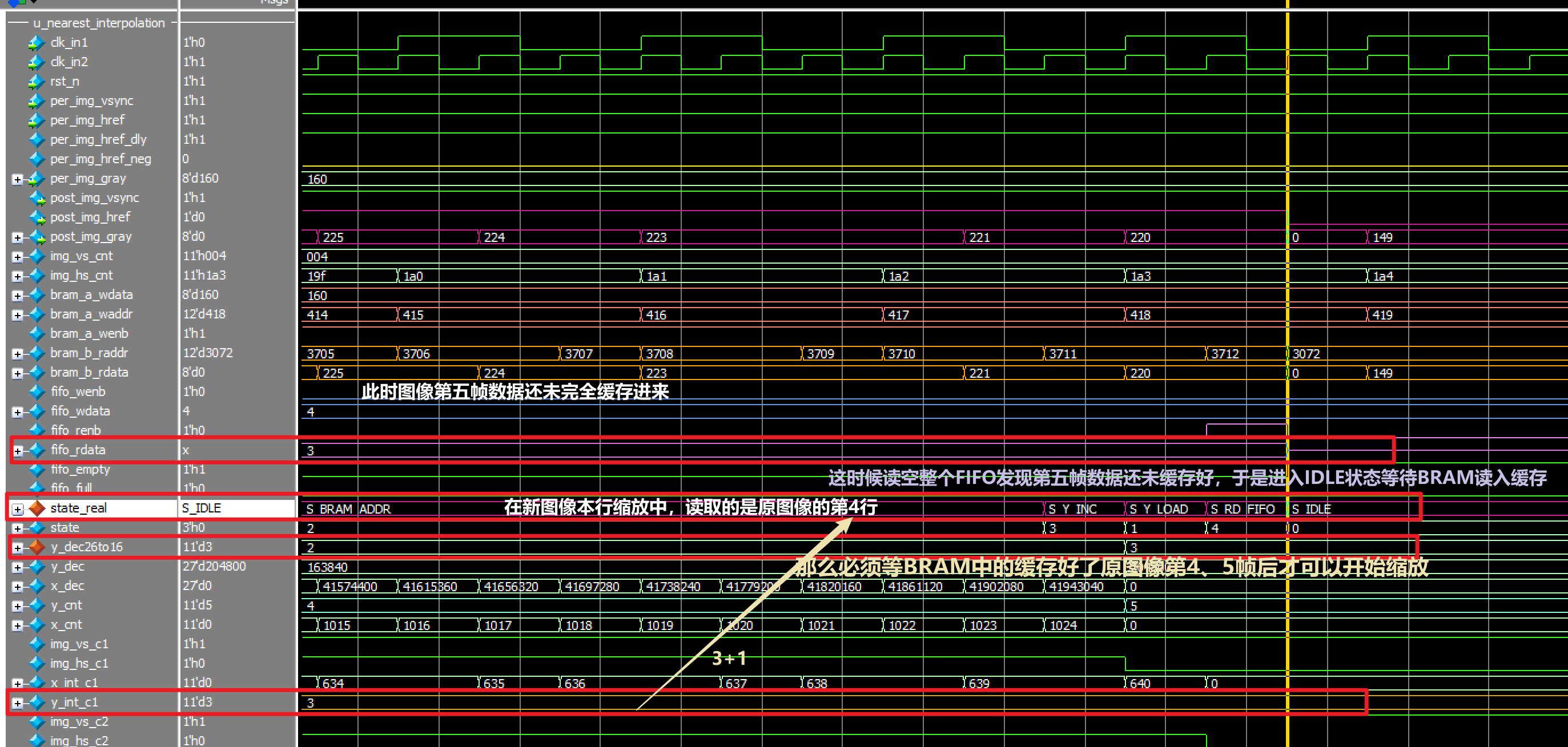
双线性插值算法
双线性插值算法常用来对图像进行缩放, 其核心思想是在水平和垂直两个方向上分别进行一次线性插值
双线性插值算法具有平滑功能,能有效地克服最近邻插值算法的不足,边缘处的过渡比较自然,不会出现像素值不连续的情况。因此,缩放后的图像质量较高,但计算量较大,且会退化图像的高频部分,使图像细节变模糊。
双线性插值算法根据$P(x_0,y_0)$的4个相邻点$(x,y)$、$(x+1,y)$、$(x,y+1)$、$(x+1,y+1)$的灰度值$I_{11}$、$I_{12}$、$I_{21}$、$I_{21}$,通过两次插值计算得出$P(x_0,y_0)$的灰度值$I_0$
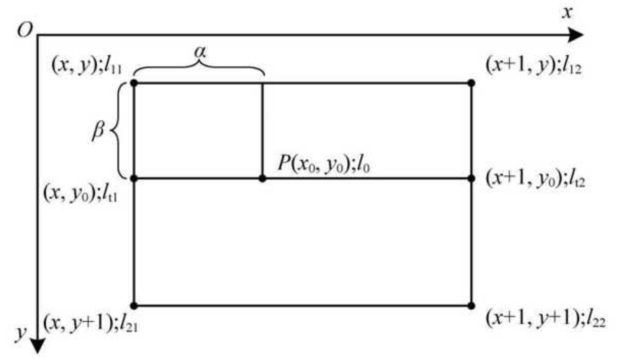
具体计算过程如下:
计算$\alpha$和$\beta$,分别为$x_0$和$y_0$的小数部分
根据$I_{11}$和$I_{21}$的插值求点$(x,y_0)$的灰度值$I_{t1}$
根据$I_{12}$和$I_{21}$的插值求点$(x+1,y_0)$的灰度值$I_{t2}$
根据$I_{t1}$和$I_{t2}$的插值求点$P(x_0,y_0)$的灰度值$I_0$
上述计算过程用矩阵表示为
其中,
浮点版的matlab实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24function [img2] = Bilinear_Interpolation(img1,row_num1,col_num1,row_num2,col_num2)
% 扩展图像是为了后面插值时避免越界
img1 = [img1;img1(row_num1,:)]; % 底部扩展一行,直接拷贝最后一行
img1 = [img1,img1(:,col_num1)]; % 右侧扩展一列,直接拷贝最后一列
img1 = double(img1);
x_ratio = col_num1/col_num2;
y_ratio = row_num1/row_num2;
for i = 1 : row_num2
y = fix((i-1)*y_ratio) + 1;
dv = (i-1)*y_ratio - fix((i-1)*y_ratio);
A = [1-dv,dv];
for j = 1 : col_num2
x = fix((j-1)*x_ratio) + 1;
du = (j-1)*x_ratio - fix((j-1)*x_ratio);
C = [1-du;du];
B = img1(y:y+1,x:x+1);
img2(i,j) = A*B*C;
end
end
img2 = uint8(img2);
其实就是在最近邻插值的基础上,本来最近邻插值是通过四舍五入round在原图像上找像素点,现在是通过fix找到对应像素点后,保留以该像素点为左上角的四个像素点,通过对该$2\times 2$区域乘以相应的权重求和后,即可得到缩放后的点
1.双线性插值的MATLAB实现
双线性插值的matlab定点实现版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24function [img2] = Bilinear_Interpolation_Int(img1,row_num1,col_num1,row_num2,col_num2)
% 扩展图像是为了后面插值时避免越界
img1 = [img1;img1(row_num1,:)]; % 底部扩展一行,直接拷贝最后一行
img1 = [img1,img1(:,col_num1)]; % 右侧扩展一列,直接拷贝最后一列
img1 = double(img1);
x_ratio = floor(col_num1/col_num2*2^16)/2^16;
y_ratio = floor(row_num1/row_num2*2^16)/2^16;
for i = 1 : row_num2
y = fix((i-1)*y_ratio) + 1;
dv = (i-1)*y_ratio - fix((i-1)*y_ratio);
A = [1-dv,dv];
for j = 1 : col_num2
x = fix((j-1)*x_ratio) + 1;
du = (j-1)*x_ratio - fix((j-1)*x_ratio);
C = [1-du;du];
B = img1(y:y+1,x:x+1);
img2(i,j) = A*B*C;
end
end
img2 = uint8(img2);
2.双线性插值的FPGA实现
在最近邻插值FPGA实现基础上理解双线性插值就比较容易了
双线性插值放大算法的实现分解为以下几步:
对原始图像进行缓存:双线性插值放大时需要同时从BRAM中读出近邻4个像素, 为了降低设计难度, 采用4个BRAM对图像进行行缓存, 每个BRAM分别输出近邻4个像素中的其中1个。 BRAM的行存储结构与最近邻插值一致。其中图像奇数行像素同时存于BRAM0和BRAM1中,偶数行像素同时存于BRAM2和BRAM3中。
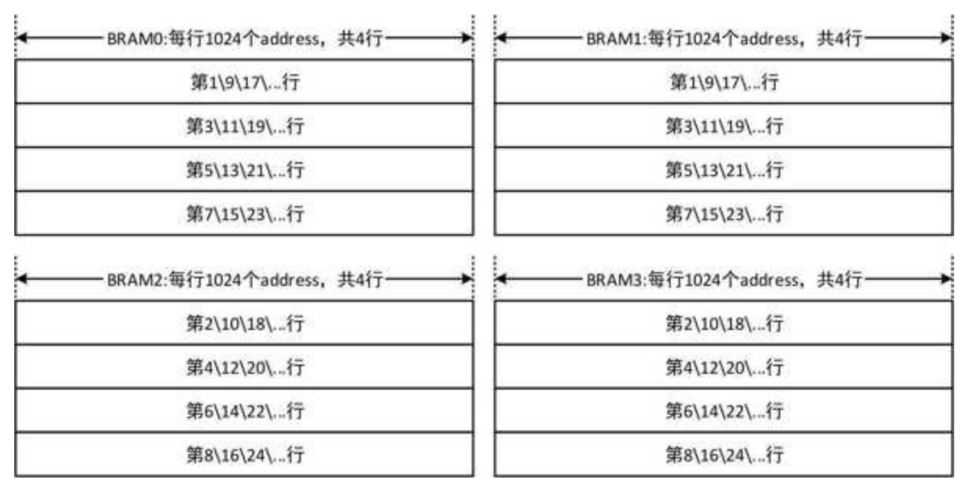
BRAM写地址的计算公式为:
- 其中,$img_hs_cnt$用于产生行内像素的地址;$img_vs_cnt[2:1]$用于产生不同行的基地址,而$img_vs_cnt[0]$用来指示写BRAM0/1($img_vs_cnt[0]==0$)还是BRAM2/3($img_vs_cnt[0]==1$)(绝妙啊)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26reg [11:0] bram_a_waddr;
always @(posedge clk_in1)
begin
bram_a_waddr <= {img_vs_cnt[2:1],10'b0} + img_hs_cnt;
end
reg bram1_a_wenb;
always @(posedge clk_in1)
begin
if(rst_n == 1'b0)
bram1_a_wenb <= 1'b0;
else
bram1_a_wenb <= per_img_vsync & per_img_href & ~img_vs_cnt[0];
end
reg bram2_a_wenb;
always @(posedge clk_in1)
begin
if(rst_n == 1'b0)
bram2_a_wenb <= 1'b0;
else
bram2_a_wenb <= per_img_vsync & per_img_href & img_vs_cnt[0];
end当每行像素缓存到BRAM后,将行统计$img_vs_cnt$作为标签存入异步FIFO中。后续进行双线性插值放大算法时,会根据该标签判断BRAM中是否已经缓存了插值所需要的两行像素
在进行最近邻插值放大之前,需要计算原始图像与目标图像在水平方向和垂直方向上的比率(即目标图像映射到原始图像的坐标步进)$C_X_RATIO$和$C_Y_RATIO$。已知原始图像的分辨率为$640\times 480$、目标图像的分辨率为$1024\times 768$,且要求将比率定标为16位小数,故$C_X_RATIO$和$C_Y_RATIO$的计算结果为:
用与最近邻插值法相同的一个状态机来控制BRAM的读取
根据$(y_dec,x_dec)$可以得到近邻4个像素中左上角像素的像素级坐标$(y_int_c1,x_int_c1)$ , 以及由$(y_dec,x_dec)$计算出的前述$A$与$C$(根据小数部分得出)
1
2
3
4
5
6
7
8
9always @(posedge clk_in2)
begin
x_int_c1 <= x_dec[25:16];
y_int_c1 <= y_dec[25:16];
x_fra_c1 <= {1'b0,x_dec[15:0]}; //\alpha
inv_x_fra_c1 <= 17'h10000 - {1'b0,x_dec[15:0]}; //1-\alpha
y_fra_c1 <= {1'b0,y_dec[15:0]}; //\beta
inv_y_fra_c1 <= 17'h10000 - {1'b0,y_dec[15:0]}; ///1-\beta
end将$(y_int_c1,x_int_c1)$ 转为BRAM的读地址$bram_addr_c2$(用于指示左上角像素位于图像奇数行或偶数行, 其值为0时表示奇数行, 为1时表示偶数行 ), 以及根据$x_fra_c1$、$inv_x_fra_c1$、 $y_fra_c1$、 $inv_y_fra_c1$计算近邻4个像素的权重$frac_00_c2$、 $frac_01_c2$、$frac_10_c2$、 $frac_11_c2$,将$ABC$矩阵相乘后展开后,就可以得到原像素点$B$对应的一个$2\times 2$点乘权重
1
2
3
4
5
6
7
8
9always @(posedge clk_in2)
begin
bram_addr_c2 <= {y_int_c1[2:1],10'b0} + x_int_c1;
frac_00_c2 <= inv_x_fra_c1 * inv_y_fra_c1;
frac_01_c2 <= x_fra_c1 * inv_y_fra_c1;
frac_10_c2 <= inv_x_fra_c1 * y_fra_c1;
frac_11_c2 <= x_fra_c1 * y_fra_c1;
bram_mode_c2 <= y_int_c1[0];
end根据$bram_addr_c2$产生近邻4个像素在4个BRAM中的读地址
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17always @(posedge clk_in2)
begin
if(bram_mode_c2 == 1'b0)
begin
even_bram1_b_raddr <= bram_addr_c2;
odd_bram1_b_raddr <= bram_addr_c2 + 1'b1;
even_bram2_b_raddr <= bram_addr_c2;
odd_bram2_b_raddr <= bram_addr_c2 + 1'b1;
end
else
begin
even_bram1_b_raddr <= bram_addr_c2 + 11'd1024;
odd_bram1_b_raddr <= bram_addr_c2 + 11'd1025;
even_bram2_b_raddr <= bram_addr_c2;
odd_bram2_b_raddr <= bram_addr_c2 + 1'b1;
end
end根据4个BRAM的读地址从BRAM中读出4个像素并映射到近邻4个像素的位置上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17always @(posedge clk_in2)
begin
if(bram_mode_c4 == 1'b0)
begin
pixel_data00_c5 <= even_bram1_b_rdata;
pixel_data01_c5 <= odd_bram1_b_rdata;
pixel_data10_c5 <= even_bram2_b_rdata;
pixel_data11_c5 <= odd_bram2_b_rdata;
end
else
begin
pixel_data00_c5 <= even_bram2_b_rdata;
pixel_data01_c5 <= odd_bram2_b_rdata;
pixel_data10_c5 <= even_bram1_b_rdata;
pixel_data11_c5 <= odd_bram1_b_rdata;
end
end得到的近邻4个像素中可能存在像素超出图像边界的情况,需要进行像素的边界复制,像素越界处理。
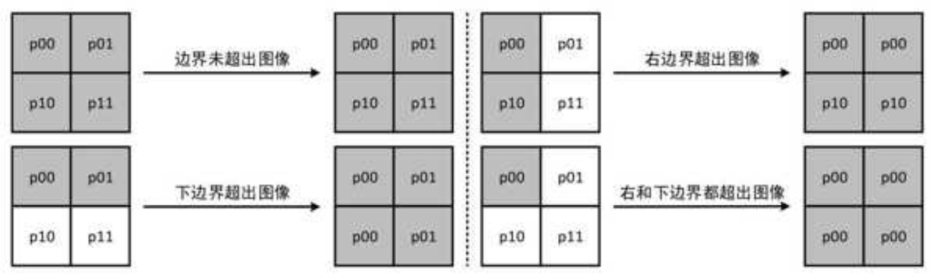
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33always @(posedge clk_in2)
begin
case({right_pixel_extand_flag_c5,bottom_pixel_extand_flag_c5})
2'b00 :
begin
pixel_data00_c6 <= pixel_data00_c5;
pixel_data01_c6 <= pixel_data01_c5;
pixel_data10_c6 <= pixel_data10_c5;
pixel_data11_c6 <= pixel_data11_c5;
end
2'b01 :
begin
pixel_data00_c6 <= pixel_data00_c5;
pixel_data01_c6 <= pixel_data01_c5;
pixel_data10_c6 <= pixel_data00_c5;
pixel_data11_c6 <= pixel_data01_c5;
end
2'b10 :
begin
pixel_data00_c6 <= pixel_data00_c5;
pixel_data01_c6 <= pixel_data00_c5;
pixel_data10_c6 <= pixel_data10_c5;
pixel_data11_c6 <= pixel_data10_c5;
end
2'b11 :
begin
pixel_data00_c6 <= pixel_data00_c5;
pixel_data01_c6 <= pixel_data00_c5;
pixel_data10_c6 <= pixel_data00_c5;
pixel_data11_c6 <= pixel_data00_c5;
end
endcase
end将近邻4个像素与各自的权重相乘后累加, 得到目标像素的灰度值
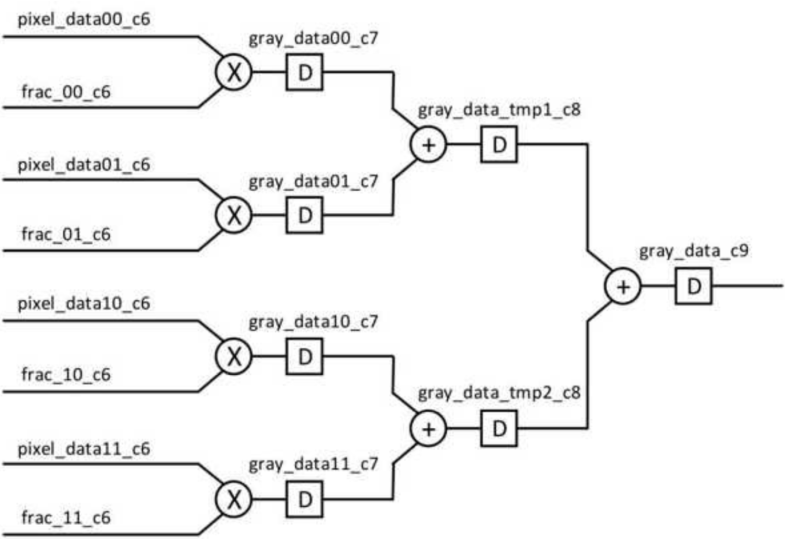
1
2
3
4always @(posedge clk_in2)
begin
gray_data_c10 <= gray_data_c9[43:32] + gray_data_c9[31];
end- 这里有对得到的目标像素点缩小$2^{32}$倍,因为$A$和$B$都是小数,它们在定点计算时,均被放大了$2^{16}$倍
目标像素的灰度值可能大于255,为了避免像素值越界,将灰度值大于255的像素,直接输出255,灰度值越界处理
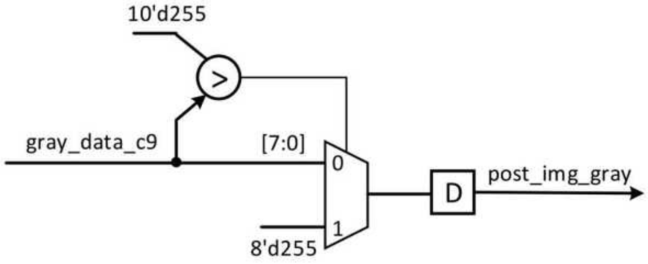
1
2
3
4
5
6
7always @(posedge clk_in2)
begin
if(gray_data_c10 > 12'd255)
post_img_gray <= 8'd255;
else
post_img_gray <= gray_data_c10[7:0];
end
仿真结果:
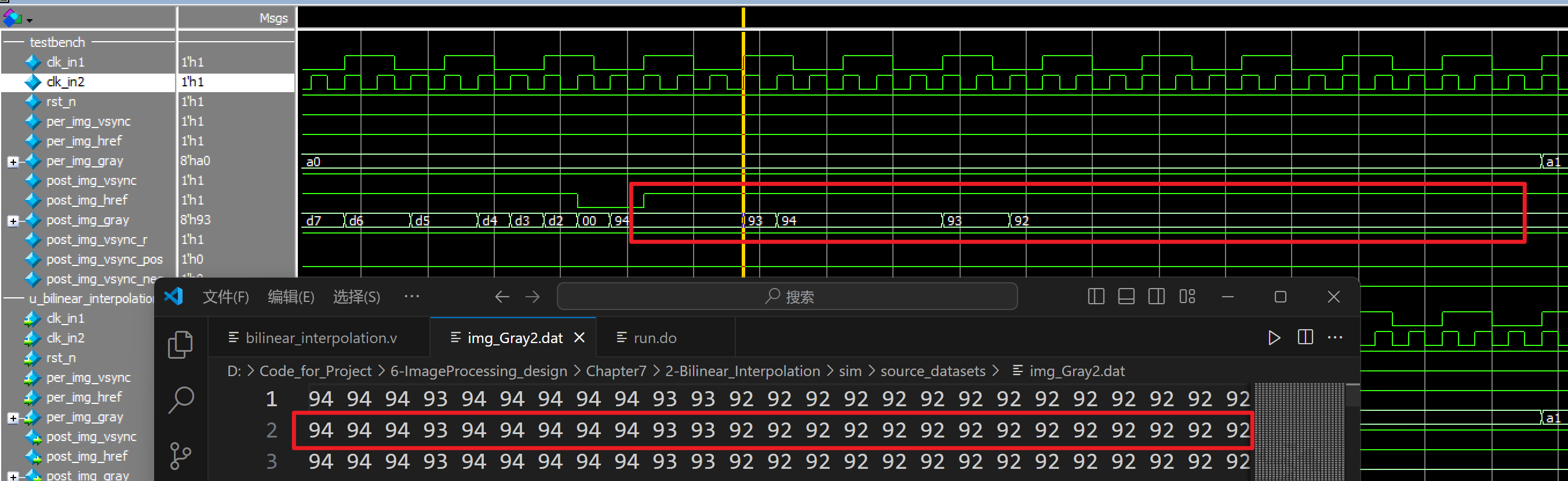
双三次插值算法
双三次插值算法既要考虑点 $P (x_0 ,y_0)$的直接邻点对它的影响, 也要考虑该点周围16个邻点的灰度值对它的影响
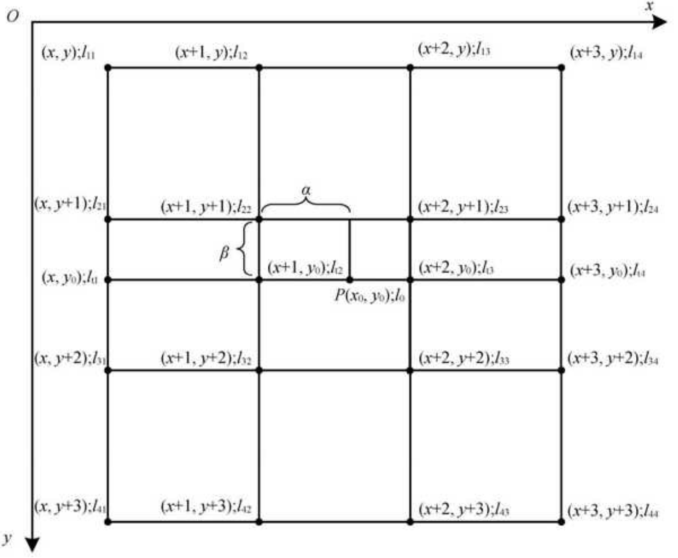
- 其中$\alpha$为$x_0$的小数部分, $\beta$为$y_0$的小数部分。 双三次插值算法需要找出这16个像素对于点$P$像素值的影响因子, 并根据影响因子计算目标点的像素值, 从而达到图像缩放的目的。
与双线性插值算法一致,其也有一定类似的计算矩阵,此处不再赘述
matlab代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39function [img2] = Bicubic_Interpolation(img1,row_num1,col_num1,row_num2,col_num2)
% 扩展图像是为了后面插值时避免越界
img1 = [img1;img1(row_num1,:);img1(row_num1,:)]; % 底部扩展两行,直接拷贝最后一行
img1 = [img1(1,:);img1]; % 顶部扩展一行,直接拷贝第一行
img1 = [img1,img1(:,col_num1),img1(:,col_num1)]; % 右侧扩展两列,直接拷贝最后一列
img1 = [img1(:,1),img1]; % 左侧扩展一列,直接拷贝第一列
img1 = double(img1);
x_ratio = col_num1/col_num2;
y_ratio = row_num1/row_num2;
for i = 1 : row_num2
y = fix((i-1)*y_ratio) + 2;
dv = (i-1)*y_ratio - fix((i-1)*y_ratio);
A = [Weight(1+dv),Weight(dv),Weight(1-dv),Weight(2-dv)];
for j = 1 : col_num2
x = fix((j-1)*x_ratio) + 2;
du = (j-1)*x_ratio - fix((j-1)*x_ratio);
C = [Weight(1+du);Weight(du);Weight(1-du);Weight(2-du)];
B = img1(y-1:y+2,x-1:x+2);
img2(i,j) = A*B*C;
end
end
img2 = uint8(img2);
function [B] = Weight(A)
A = abs(A);
a = -0.5;
if (A <= 1)
B = (a+2)*A^3 - (a+3)*A^2 + 1;
elseif (A < 2)
B = a*A^3 - 5*a*A^2 + 8*a*A - 4*a;
else
B = 0;
end
Reference
- 《基于MATLAB与FPGA的图像处理教程》图书及其配套资料
