本节主要对通信系统中常见的校验模块进行学习,主要包括CRC与ECC校验。由于本人能力有限,暂时只是会用其校验方法,具体推导还没了解清楚,如果今后有时间更深入了解,将及时在此篇文章中补充。
CRC校验(循环冗余校验)
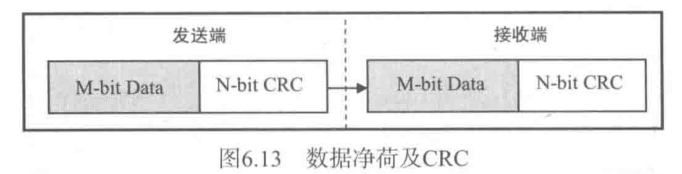
CRC是数据帧传输中常用的一种差错控制编码方式,针对要发送的数据帧,使用一些特定的多项式可以计算出CRC校验结果
CRC校验结果和原始数据一起传输到接收端,接收端在接收数据的同时按照相同的多项式对接收数据进行校验运算,并将校验结果和接收的结果进行对比:
- 如果二者相同,则认为没有发生传输错误;
- 如果不同,则认为发生了传输错误
- 从理论上说,如果接收端计算出的CRC值与接收到的CRC值匹配,数据中仍有出错的可能,但是由于这种可能性极低,在实际应用中可以视为0,即没有错误发生
关于CRC计算校验子的规则到底是怎样的(其实就是移位+异或),可以看ex_16_1汉明纠错码原理以及一步一步分析实现纠错码;_哔哩哔哩_bilibili视频30mins左右开始的内容(但其实懂了这个,我也还是不明白最终映射到电路上如何成了LFSR那样的结果,不过会就行,聪明的人已经为我们推导完了,不用纠结,虽然我纠结了很久还没弄懂)
CRC校验的硬件实现一般分为串行和并行两种,在串行实现方法中使用到了LFSR寄存器,所以下面从LFSR寄存器的介绍开始,介绍其实现方法。
1.LFSR寄存器
LFSR的特征多项式
一个$n$级LFSR(寄存器的个数)最多只有$2^n - 1$个状态,即:一个$n$级的LFSR最多只能遍历$2^n-1$个序列,即最大周期为$2^n-1$($n$bit移位寄存器能存储的数据为$0\sim 2^n-1$,即$2^n$个状态,但是由于LFSR禁止全0状态,因此一个$n$级的LFSR最多只能有$2^n - 1$个状态,因此一个LFSR的最大周期是$2^n-1$个系统时钟周期)
当使用LFSR产生PRBS(伪随机噪声)时,是存在周期性的。值得注意的是:不是所有的LFSR都能达到$2^n-1$个周期,这与抽头的设计相关,只要选择合适的反馈函数便可使序列周期达到$2^n-1$,周期达到最大值的序列称为$m$序列
LFSR寄存器又分为两类:
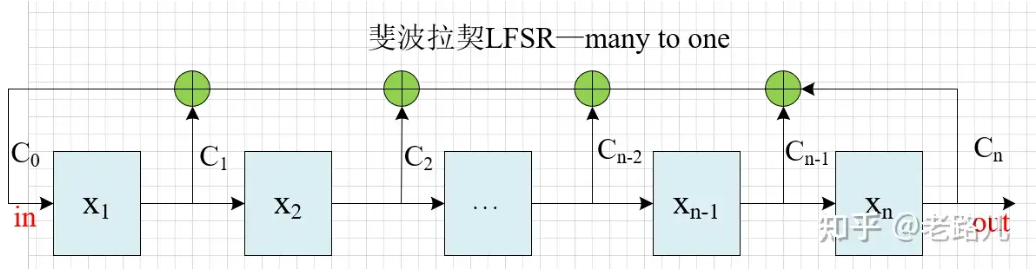
- 斐波那契LFSR:多到一型LFSR(many to one)
- 伽罗瓦LFSR:一到多型LFSR(one to many)
- 伽罗瓦LFSR具有更高的速度,因为两个触发器之间只有一个异或门。斐波那契LFSR在首尾两个寄存器之间有多个异或门,组合逻辑延时更大。
1.1 斐波那契LFSR
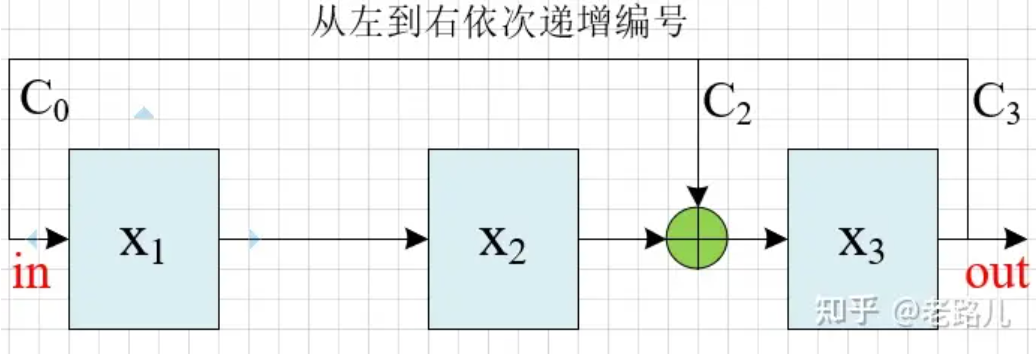
斐波那契LFSR:抽头序列对应bit位置的多个寄存器的输出异或后驱动一个寄存器输入
从左至右依次递增编号:
从左至右依次递减编号:
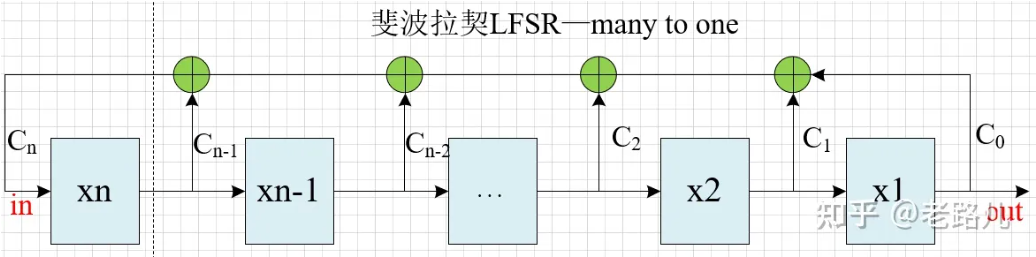
以三级LFSR,反馈函数:$f(x) = x^3+ x^2 + 1$ 为例,其两种编号的斐波那契电路图如下:
从左至右依次递增编号:
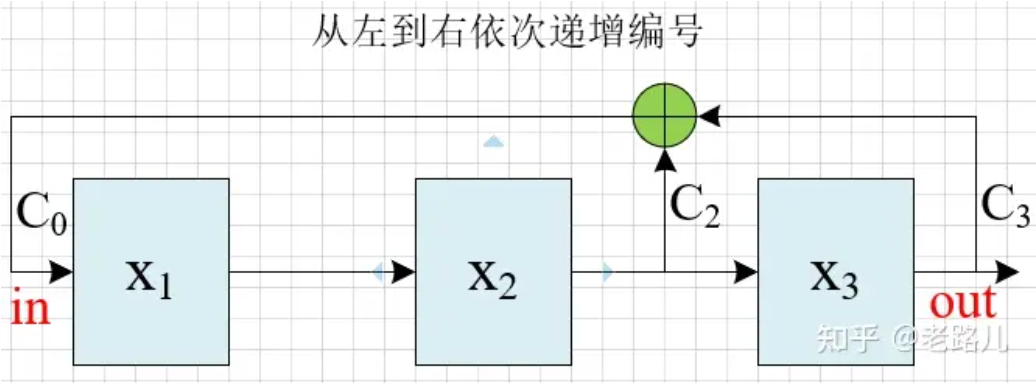
假设初始状态为001,则该电路的状态跳转为:

从左至右依次递减编号:
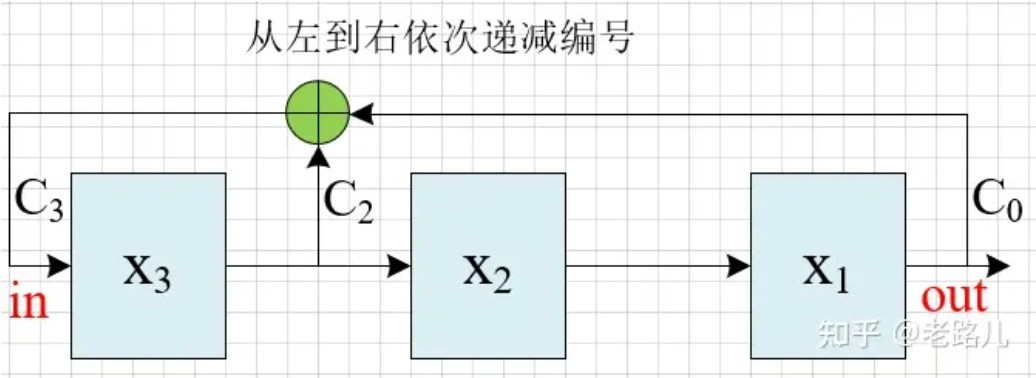
假设初始状态为001,则该电路的状态跳转为:

斐波那契LFSR习惯采用“从左到右依次递增编号”的电路
1.2 伽罗瓦LFSR
伽罗瓦LFSR:最后一个寄存器的输出通过与抽头序列对应位置寄存器前一级寄存器的输出异或后驱动多个抽头序列对应位置的寄存器
从左至右依次递增编号:
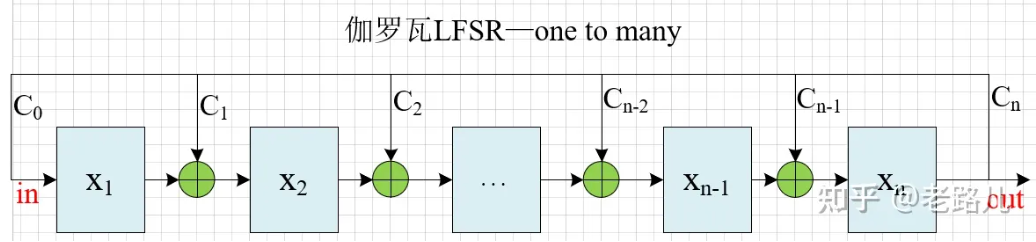
从左至右依次递减编号:
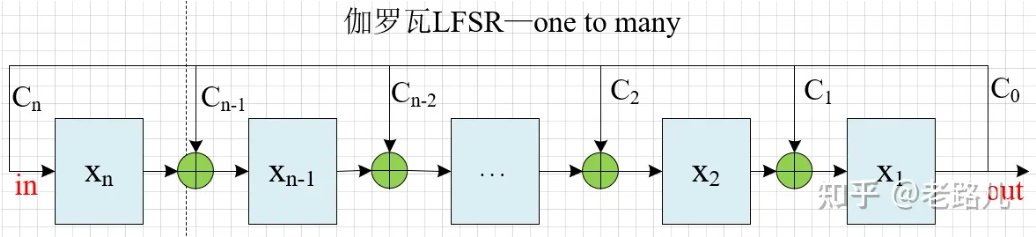
同样,以三级LFSR,反馈函数:$f(x) = x^3+ x^2 + 1$ 为例,其两种编号的伽罗瓦电路图如下:
从左至右依次递增编号:
假设初始状态为001,则该电路的状态跳转为:

从左至右依次递减编号:
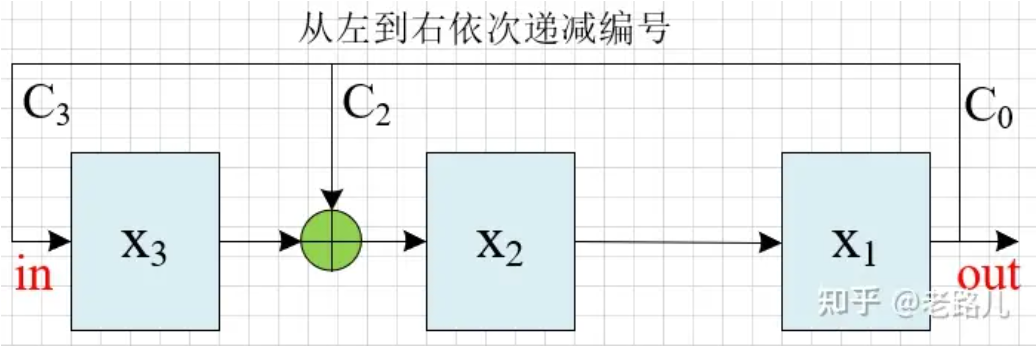
假设初始状态为001,则该电路的状态跳转为:

伽罗瓦LFSR习惯采用“从左到右依次递减编号”电路
2.串行CRC的实现
串行CRC8(以多项式$x^8+x^2+x+1$为例)硬件实现的原理图如下:
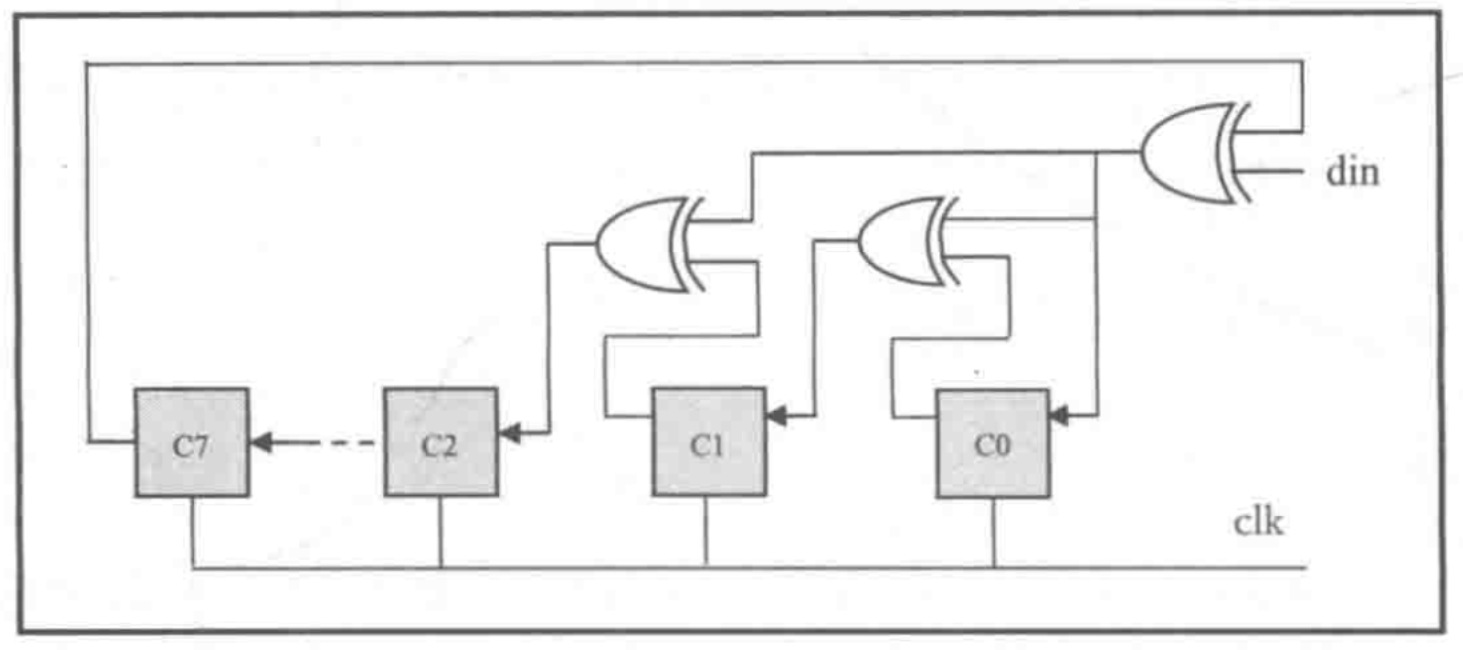
其实这个结构具体是怎么跟CRC计算的底层原理对应上的,我也没弄太懂,但是呢,其实它和前文中一到多的LFSR结构一样,只是在输出寄存器反馈到各级寄存器之前与din异或了。那么在不懂底层原理的情况下,其实根据LFSR的知识,再加个异或,也是能画出来原理图来的,然后再照着原理图写代码就可以了。
值得注意的是,din送数据时是最高bit先进
2.1源代码
1 |
|
2.2 testbench
1 |
|
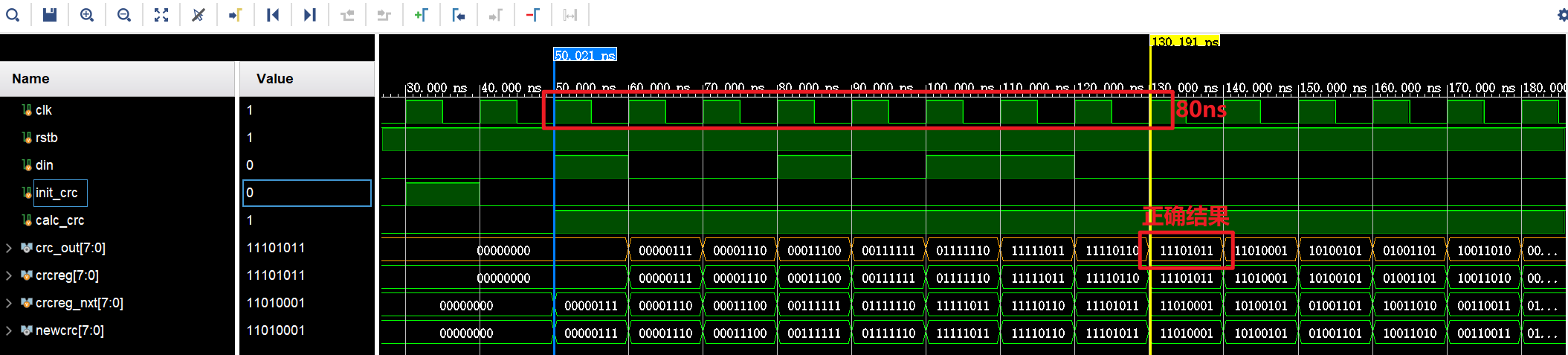
结果如下:
3.并行CRC的实现
- 在网上看了很多并行CRC的推导步骤,遗憾的是个人能力有限,没有一个是能完全看懂的,不过其实不懂也没关系,最愚蠢的推导方式就是对串行CRC的公式进行迭代,应该就是能推导出来的
- 网上有很多并行CRC代码生成的网站及小程序,这里推荐一个目前还能用的:OutputLogic.com » CRC Generator
可以通过CRC校验码在线计算网站验证:CRC(循环冗余校验)在线计算_ip33.com
仿真仿真着有个重大发现,原来并行CRC是可以用$m$个小位宽(比如$n$位宽)的数经过$m$个周期的延时求出的CRC等效为$m\times n$位宽数据对应的校验码
- 下面以OutputLogic.com网站上生成的$x^8+x^2+x+1$的初始值为0的CRC代码为例,仿真分析(网站上默认的初始值是ff,我将其改为00了)
3.1 源代码
1 |
|
3.2 testbench
1 |
|
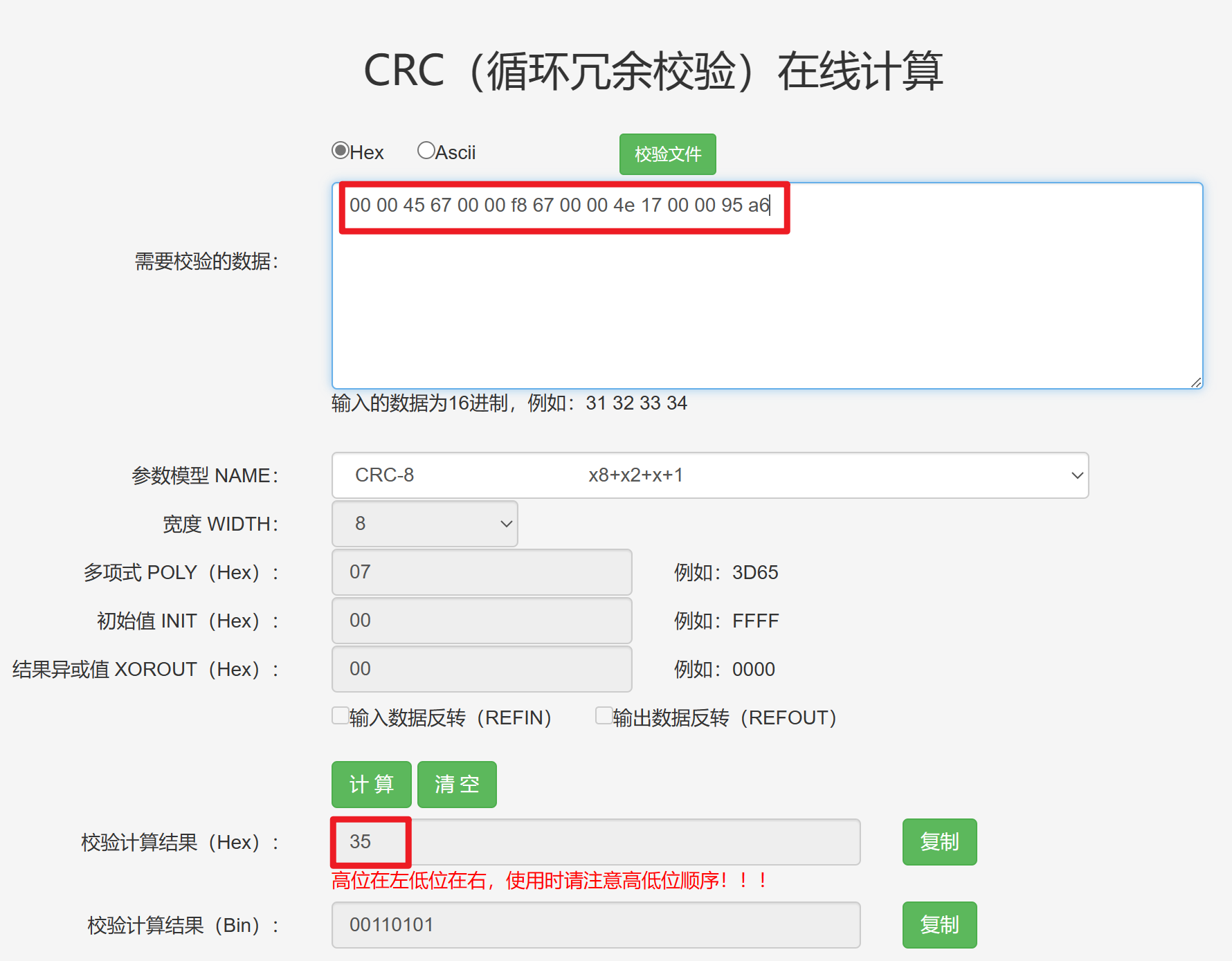
结果如下:

结果分析:可以得到最终结果为0h35,其也是00004567_0000f867_00004e17_000095a6对应的校验码。但每个时钟周期实际上只计算了32bit,经过4个时钟周期后,即可计算出$32\times 4 =128$bit对应的校验码。其实,个人感觉当前每32bit的输出就作为下次32bit的初始值。值得注意的是,从最高32bit开始送入
这里还PS一下,一开始我并没有发现可以用小位宽不断迭代生成大位宽对应的校验码,以为只能是每个时钟周期都能计算出一个小位宽的结果,每个周期输出的结果与结果直接并无联系,还愚蠢的将代码改成如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
module parallel_crc8(
input clk,
input rst_n,
input [31:0] data_in,
input crc_en,
output [7:0] crc_out
);
localparam CRC_INIT_VALUE = 8'h00;
reg [7:0] lfsr_q,lfsr_c;
assign crc_out = lfsr_q;
always @(*) begin
lfsr_c[0] = CRC_INIT_VALUE[4] ^ CRC_INIT_VALUE[6] ^ CRC_INIT_VALUE[7] ^ data_in[0] ^ data_in[6] ^ data_in[7] ^ data_in[8] ^ data_in[12] ^ data_in[14] ^ data_in[16] ^ data_in[18] ^ data_in[19] ^ data_in[21] ^ data_in[23] ^ data_in[28] ^ data_in[30] ^ data_in[31];
lfsr_c[1] = CRC_INIT_VALUE[0] ^ CRC_INIT_VALUE[4] ^ CRC_INIT_VALUE[5] ^ CRC_INIT_VALUE[6] ^ data_in[0] ^ data_in[1] ^ data_in[6] ^ data_in[9] ^ data_in[12] ^ data_in[13] ^ data_in[14] ^ data_in[15] ^ data_in[16] ^ data_in[17] ^ data_in[18] ^ data_in[20] ^ data_in[21] ^ data_in[22] ^ data_in[23] ^ data_in[24] ^ data_in[28] ^ data_in[29] ^ data_in[30];
lfsr_c[2] = CRC_INIT_VALUE[0] ^ CRC_INIT_VALUE[1] ^ CRC_INIT_VALUE[4] ^ CRC_INIT_VALUE[5] ^ data_in[0] ^ data_in[1] ^ data_in[2] ^ data_in[6] ^ data_in[8] ^ data_in[10] ^ data_in[12] ^ data_in[13] ^ data_in[15] ^ data_in[17] ^ data_in[22] ^ data_in[24] ^ data_in[25] ^ data_in[28] ^ data_in[29];
lfsr_c[3] = CRC_INIT_VALUE[1] ^ CRC_INIT_VALUE[2] ^ CRC_INIT_VALUE[5] ^ CRC_INIT_VALUE[6] ^ data_in[1] ^ data_in[2] ^ data_in[3] ^ data_in[7] ^ data_in[9] ^ data_in[11] ^ data_in[13] ^ data_in[14] ^ data_in[16] ^ data_in[18] ^ data_in[23] ^ data_in[25] ^ data_in[26] ^ data_in[29] ^ data_in[30];
lfsr_c[4] = CRC_INIT_VALUE[0] ^ CRC_INIT_VALUE[2] ^ CRC_INIT_VALUE[3] ^ CRC_INIT_VALUE[6] ^ CRC_INIT_VALUE[7] ^ data_in[2] ^ data_in[3] ^ data_in[4] ^ data_in[8] ^ data_in[10] ^ data_in[12] ^ data_in[14] ^ data_in[15] ^ data_in[17] ^ data_in[19] ^ data_in[24] ^ data_in[26] ^ data_in[27] ^ data_in[30] ^ data_in[31];
lfsr_c[5] = CRC_INIT_VALUE[1] ^ CRC_INIT_VALUE[3] ^ CRC_INIT_VALUE[4] ^ CRC_INIT_VALUE[7] ^ data_in[3] ^ data_in[4] ^ data_in[5] ^ data_in[9] ^ data_in[11] ^ data_in[13] ^ data_in[15] ^ data_in[16] ^ data_in[18] ^ data_in[20] ^ data_in[25] ^ data_in[27] ^ data_in[28] ^ data_in[31];
lfsr_c[6] = CRC_INIT_VALUE[2] ^ CRC_INIT_VALUE[4] ^ CRC_INIT_VALUE[5] ^ data_in[4] ^ data_in[5] ^ data_in[6] ^ data_in[10] ^ data_in[12] ^ data_in[14] ^ data_in[16] ^ data_in[17] ^ data_in[19] ^ data_in[21] ^ data_in[26] ^ data_in[28] ^ data_in[29];
lfsr_c[7] = CRC_INIT_VALUE[3] ^ CRC_INIT_VALUE[5] ^ CRC_INIT_VALUE[6] ^ data_in[5] ^ data_in[6] ^ data_in[7] ^ data_in[11] ^ data_in[13] ^ data_in[15] ^ data_in[17] ^ data_in[18] ^ data_in[20] ^ data_in[22] ^ data_in[27] ^ data_in[29] ^ data_in[30];
end //always
always @(posedge clk or posedge rst_n) begin
if(~rst_n) begin
lfsr_q <= {8{1'b0}};
end
else begin
lfsr_q <= crc_en ? lfsr_c : lfsr_q;
end
end //always
endmodule对应仿真结果:

不过感觉其实这个修改适用于:求许多个独立的32bit数据对应的CRC校验码场景
4.Reference
ECC校验
关于ECC校验,其是基于汉明码的,它也有自己特定的计算校验子的规则,此处不再赘述,附上几篇说的比较不错的博客,看完应该能大概弄懂计算的流程了。还是截出博客中的重点吧
最详细的“ECC-汉明码”原理讲解_ecc编码-CSDN博客

史上最通俗的海明码编码计算、检错和纠错原理解析_求0101按偶校验配置的海明编码-CSDN博客
wx_article/汉明码/汉明码.md at master · Jassy930/wx_article · GitHub(这篇详细看看,整个ECC校验子的流程大概就明白了)
因为目前在比赛的项目中决定用CRC校验,所以暂时不做ECC的仿真测试,有时间有需求做了ECC的设计的话,再来此补充
附加模块编写
因为这里提到了LFSR寄存器,这里就补充LFSR计数器的编写
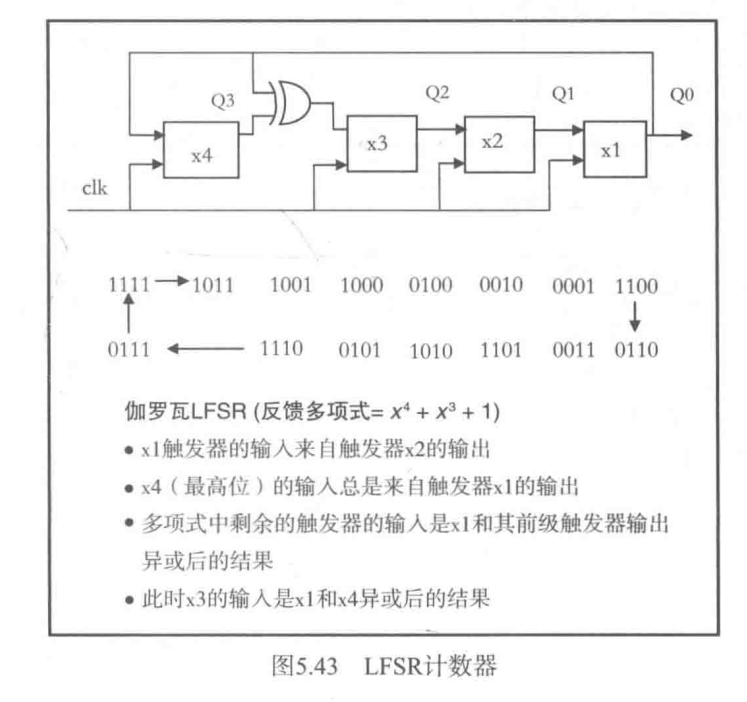
源文件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36module lfsr_counter_4bit(
input clk,
input rst_n,
input new_cntr_preset, //该信号拉高预设初值
output ctr_expired
);
reg [3 : 0] lfsr_cnt, lfsr_cnt_nxt;
wire [3 : 0] lfsr_cnt_xor;
assign lfsr_cnt_xor[0] = lfsr_cnt[1];
assign lfsr_cnt_xor[1] = lfsr_cnt[2];
assign lfsr_cnt_xor[2] = lfsr_cnt[3] ^ lfsr_cnt[0];
assign lfsr_cnt_xor[3] = lfsr_cnt[0];
always @(*) begin
if(new_cntr_preset) begin
lfsr_cnt_nxt = 4'b1111;
end
else begin
lfsr_cnt_nxt = lfsr_cnt_xor;
end
end
always @(posedge clk or negedge rst_n) begin
if(~rst_n) begin
lfsr_cnt <= 4'b1111;
end
else begin
lfsr_cnt <= lfsr_cnt_nxt;
end
end
assign ctr_expired = (lfsr_cnt == 4'b0111);
endmoduletestbench
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25module lfsr_counter_tb;
reg clk ;
reg rst_n ;
reg new_cntr_preset ;
wire ctr_expired ;
lfsr_counter_4bit lfsr_counter_4bit_u1(
.clk (clk ),
.rst_n (rst_n ),
.new_cntr_preset (new_cntr_preset ),
.ctr_expired (ctr_expired )
);
always #5 clk = ~clk;
initial begin
clk = 1;
rst_n = 0;
new_cntr_preset = 0;
#21 rst_n = 1;
end
endmodule仿真结果:

