FPGA实现CNN之卷积神经网络理论基础

本节主要介绍了卷积神经网络最基础的知识。

单层神经网络

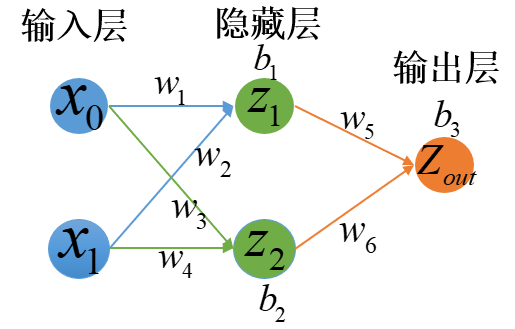
1.NN反向传播的推导

• 梯度下降的公式为：
  $$
  w=w-\alpha\cdot \frac{\partial L(w,b)}{\partial w}\
  b = b-\alpha\cdot \frac{\partial L(w,b)}{\partial b}
  $$

• 激活函数Sigmoid(x)：
  $$
  Sigmoid(x) = \frac{1}{1+e^{-x}}\
  Sigmoid’(x)= S\cdot (1-S)
  $$

• 损失函数Loss：
  $$
  L (w,b)= \frac12(Z_{out}-Z_{gold})^2\
  L’ (w,b)= (Z_{out}-Z_{gold})
  $$

  • 其中，$Zout$为神经网络的输出结果，$Z_{gold}$为神经网络的标签

• 以求$w_5$的反向传播为例（先假设学习率为1）：

  • 首先，$w_5$梯度下降公式为：
    $$
    w_5 = w_5 -\frac{\partial L(w,b)}{\partial w_5}
    $$

  • 那么，主要就是求解$\frac{\part L(w.b)}{\part w_5}$
    $$
    \begin{aligned}
    \frac{\part L(w,b)}{\part w_5} &=\frac{\part L(w,b)}{\part Z_{out}}\cdot \frac{\part Z_{out}}{\part w_5}\
    &=(Z_{out}-Z_{gold})\frac{\part Z_{out}}{\part w_5}\
    &=(Z_{out}-Z_{gold})\cdot Z_{out}\cdot(1-Z_{out})\cdot z_1
    \end{aligned}
    $$

    • 其中，$Z_{out} = S(z_1w_5+z_2w_6+b_3),\frac{\part Z_{out}}{\part w_5}=S’(z_1w_5+z_2w_6+b_3)\cdot z_1$

• 以求$w_1$的反向传播为例（先假设学习率为1）：

  • 首先，$w_1$的梯度下降公式为：
    $$
    w_1 = w_1-\frac{\part L(w,b)}{\part w_1}
    $$

  • 那么，主要就是求解$\frac{\part L(w,b)}{\part w_1}$
    $$
    \begin{aligned}
    \frac{\part L(w,b)}{\part w_1} &= \frac{\part L(w,b)}{\part Z_{out}}\frac{\part Z_{out}}{\part z_1}\frac{\part z_1}{\part w_1}\
    & = (Z_{out}-Z_{gold})\frac{\part z_{out}}{\part z_1}\frac{\part z_1}{\part w_1}\
    & = (Z_{out}-Z_{gold})\cdot (Z_{out}(1-Z_{out}))w_5\cdot\frac{\part z_1}{\part w_1}\
    & = (Z_{out}-Z_{gold})\cdot (Z_{out}(1-Z_{out}))w_5\cdot(z_1(1-z_1))x_0
    \end{aligned}
    $$

    • 其中，$z_1 = Sigmoid(w_1x_0+w_2x_1+b_1)$

2.MATLAB仿真实现

• LNN.m

  clear;clc;
  %//////// 训练集 ///////// WX - B
  data_set = [0 0 0;
              0 1 1;
              1 0 1;
              1 1 0];
  [data_set_len,~]=size(data_set);
  %/////// 常量定义 ///////
  PERCISION = 0.0001;
  ALPHA = 0.5;
  INPUT_LAYER_CNUM = 2;
  HIDDEN_LAYER_CNUM = 2;
  OUTPUT_LAYER_CNUM = 1;
  
  hidden_weights = rand(HIDDEN_LAYER_CNUM,INPUT_LAYER_CNUM + 1 );
  output_weights = rand(OUTPUT_LAYER_CNUM,HIDDEN_LAYER_CNUM + 1 );
  hidden_out=zeros(1,HIDDEN_LAYER_CNUM);
  loss = 1;
  %/////// 训练 [调整参数的过程] //////////
  while(loss > PERCISION )
      loss = 0;
      for j=1:data_set_len
          %///// 正向传播 //////
          for i=1:HIDDEN_LAYER_CNUM
              tmp=0;
              for k=1:INPUT_LAYER_CNUM
                  tmp = tmp + hidden_weights(i,k)*data_set(j,k);
              end
              tmp = tmp - hidden_weights(i,INPUT_LAYER_CNUM+1) ;
              hidden_out(1,i) = f_sigmoid(tmp);
          end
          zout = 0;
          for i=1:HIDDEN_LAYER_CNUM
              zout = zout + output_weights(1,i)*hidden_out(1,i);
          end
          zout = zout - output_weights(1,HIDDEN_LAYER_CNUM+1);
          zout = f_sigmoid(zout);
          
          %///// 反向传播 //////
          %---- 输出层反向传播 -------
          d = (zout - data_set(j,INPUT_LAYER_CNUM+1))*zout*(1-zout)*ALPHA;
          for i=1:HIDDEN_LAYER_CNUM
              output_weights(1,i) = output_weights(1,i) - d * hidden_out(1,i);
          end
          output_weights(1,HIDDEN_LAYER_CNUM+1)=output_weights(1,HIDDEN_LAYER_CNUM+1)-(-d);
          
          %---- 隐藏层反向传播 -------
          for i =1:HIDDEN_LAYER_CNUM
              dd = d*output_weights(1,i)*hidden_out(1,i)*(1-hidden_out(1,i))*ALPHA;
               for k = 1:INPUT_LAYER_CNUM
                  hidden_weights(i,k) = hidden_weights(i,k) - dd*data_set(j,k);
               end
              hidden_weights(i,INPUT_LAYER_CNUM+1) = hidden_weights(i,INPUT_LAYER_CNUM+1)-(-dd);
          end
          
          %///// 更新损失值loss //////
          loss = loss + (zout -data_set(j,INPUT_LAYER_CNUM+1))^2;
      end
      disp(loss)
  end
  
  %% /////// 预测 [检验参数的过程] //////////
  x=[1 1];
  z1 = x(1,1)*hidden_weights(1,1)+x(1,2)*hidden_weights(1,2)-hidden_weights(1,3);
  z1 = f_sigmoid(z1);
  
  z2 = x(1,1)*hidden_weights(2,1)+x(1,2)*hidden_weights(2,2)-hidden_weights(2,3);
  z2 = f_sigmoid(z2);
  
  zout_ = z1 * output_weights(1,1) + z2 * output_weights(1,2) - output_weights(1,3);
  zout_ = f_sigmoid(zout_);
  disp(zout_)
  disp(round(zout_))

• f_sigmoid.m

  function result = f_sigmoid( x )
      result = 1/(1+exp(-x));
  end

---

卷积神经网络

1.卷积层

• 存在权值共享

  

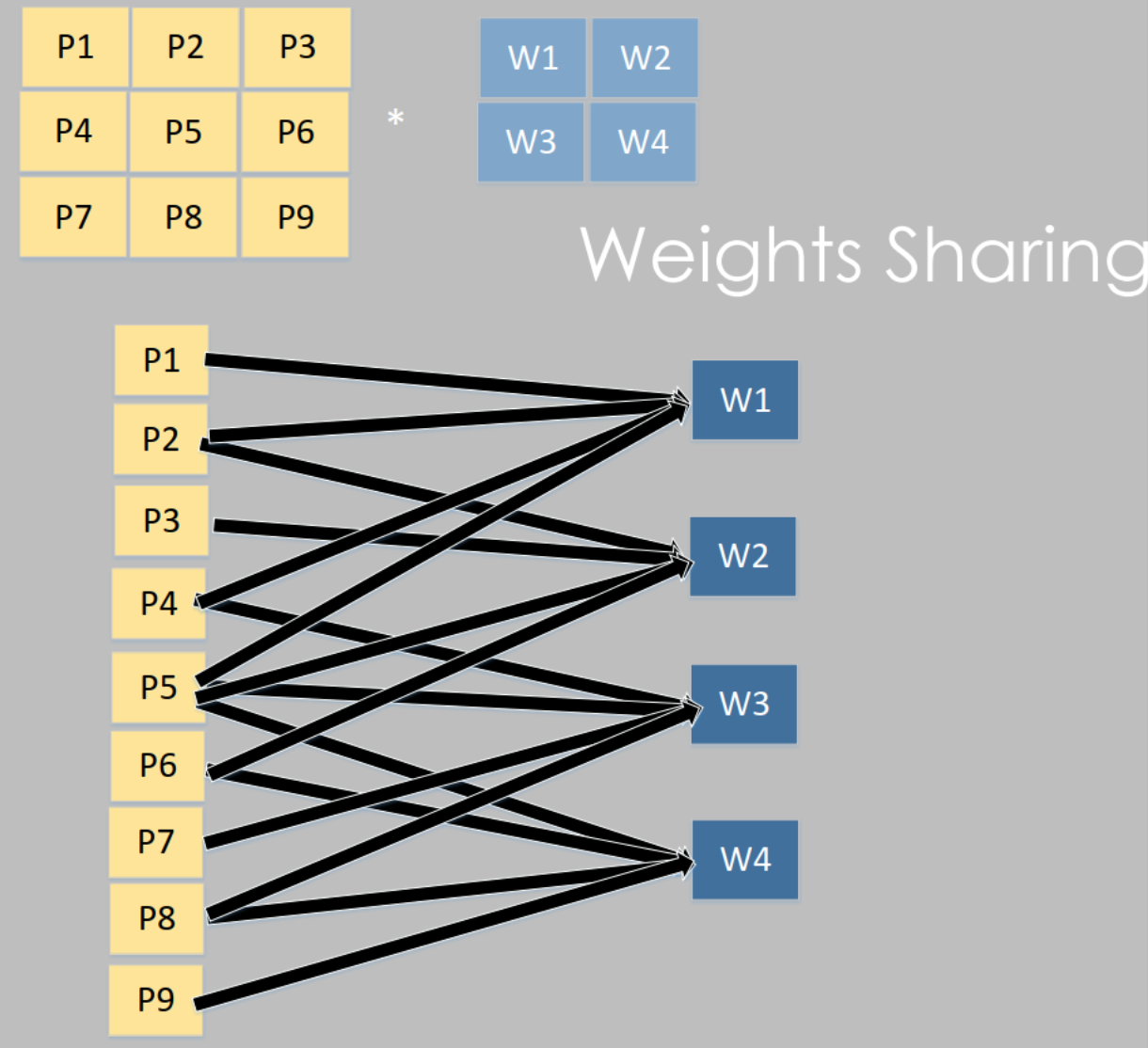
• 卷积核大小决定感受野大小

• 卷积核的数量决定所能提取特征的多少

• 卷积核的步长影响计算量以及特征提取的质量

• 卷积前后图像尺寸：

  • 设步长为s，填充为p，输入图像I的尺寸为$I_H\times I_W$，卷积核K的尺寸为$K_H\times K_W$
    $$
    W_{out} = floor(\frac{I_W+2p-K_W}{s}+1)\
    H_{out} = floor(\frac{I_H+2p-K_H}{s}+1)
    $$

    • 其中，$floor$表示向下取整

2.激活层

• 为什么需要激活层？

  • 卷积层都是线性运算，缺少非线性运算的能力
  • 并不是所有非线性函数都可以用CNN中激活的操作

• 考虑梯度消失/梯度爆炸问题

  

  • 考虑对$b_1$的反向传播，重点在于求解$\frac{\part F}{\part b_1}$

  • $y_i = \sigma(z_i) = \sigma(w_ix_i+b_i)$、$x_i = y_{i-1}$、$L$是损失函数

  • 那么，有：
    $$
    \begin{aligned}
    \frac{\part L}{\part b_1}&=\frac{\part L}{\part y_n}\frac{\part y_n}{\part z_n}\frac{\part z_n}{\part x_n}\frac{\part x_n}{\part z_{n-1}}\cdots \frac{\part z_2}{\part x_2}\frac{\part x_2}{\part z_1}\frac{\part z_1}{\part b_1}\
    &=\frac{\part L}{\part y_n}\sigma’(z_n)w_n\cdots\sigma’(z_3)w_3\sigma’(z_2)w_2\sigma’(z_1)1
    \end{aligned}
    $$

  • 梯度消失：指激活函数导数乘权重小于1时，在多层链式求导中，出现梯度快速接近0的现象

  • 梯度爆炸：指激活函数导数乘权重大于1时，在多层链式求导中，出现梯度快速增大的现象（甚至溢出）

• 激活函数选取要求：

  • 是一个非线性函数
  • 计算简单
  • 单调性
  • 可导性
  • 非饱和性：当激活函数的导数在自变量趋近于无穷大时，导数结果趋近于0，那么则称存在饱和性

• 常见的激活函数：

  • Sigmoid函数$Sigmoid(x) = \frac1{1+e^{-x}}$：
    • Sigmoid函数容易产生梯度消失
    • Sigmoid函数中有幂运算，增加计算时间
  • Tanh双曲正切函数$tanh(x) = \frac{e^x-e^{-x }}{e^x+e^{-x}}$：
    • Tanh存在梯度消失问题
    • Tanh存在计算量较大问题
  • ReLU函数：
    • ReLU函数在$x\ge 0$时，不存在梯度消失问题
    • ReLU函数计算简单

3.池化层

• 池化缩小了数据尺寸，尽可能保留原数据特征信息，数据压缩

• 抑制噪声

• 减少了所需要的训练参数，降低网络规模与复杂量

• 在空间上实现了感受野的增大，有利于提高小卷积核在大尺度特征上的提取能力

• 池化层前后图像尺寸：

  • 设步长为s，输入图像I的尺寸为$I_H\times I_W$，池化尺寸为K
    $$
    W_{out} = floor(\frac{I_W-K}{s}+1)\
    H_{out} = floor(\frac{I_H-K}{s}+1)
    $$

4.CNN的反向传播推导