FPGA数字信号处理之脉动阵列

本节主要介绍了脉冲阵列的基本结构以及其实现矩阵乘法和卷积操作的原理。

脉动阵列的基本原理

• 脉动阵列本质是结构简单的流水线，其工作过程可看作是数据在时钟的驱动下像脉搏一般在阵列中向前跳动

  

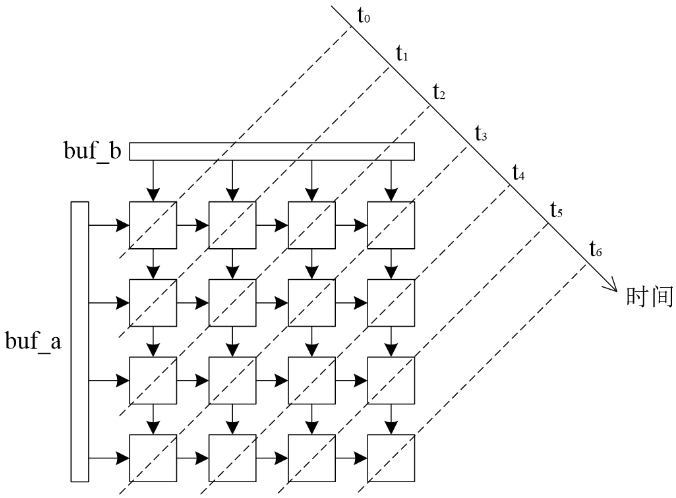
脉动阵列实现矩阵乘法

1.模式一：中间结果存储在脉动阵列单元中

• 在脉动阵列流动的是输入和权重，而每一步的结果保存在脉动计算单元中

1.1 实现思路

• 模式一：脉动阵列计算矩阵乘法的初始状态

  

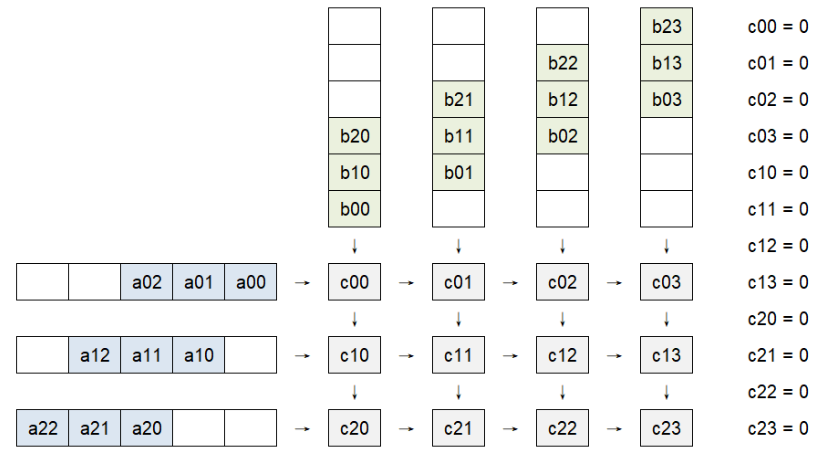
• 实现架构

  

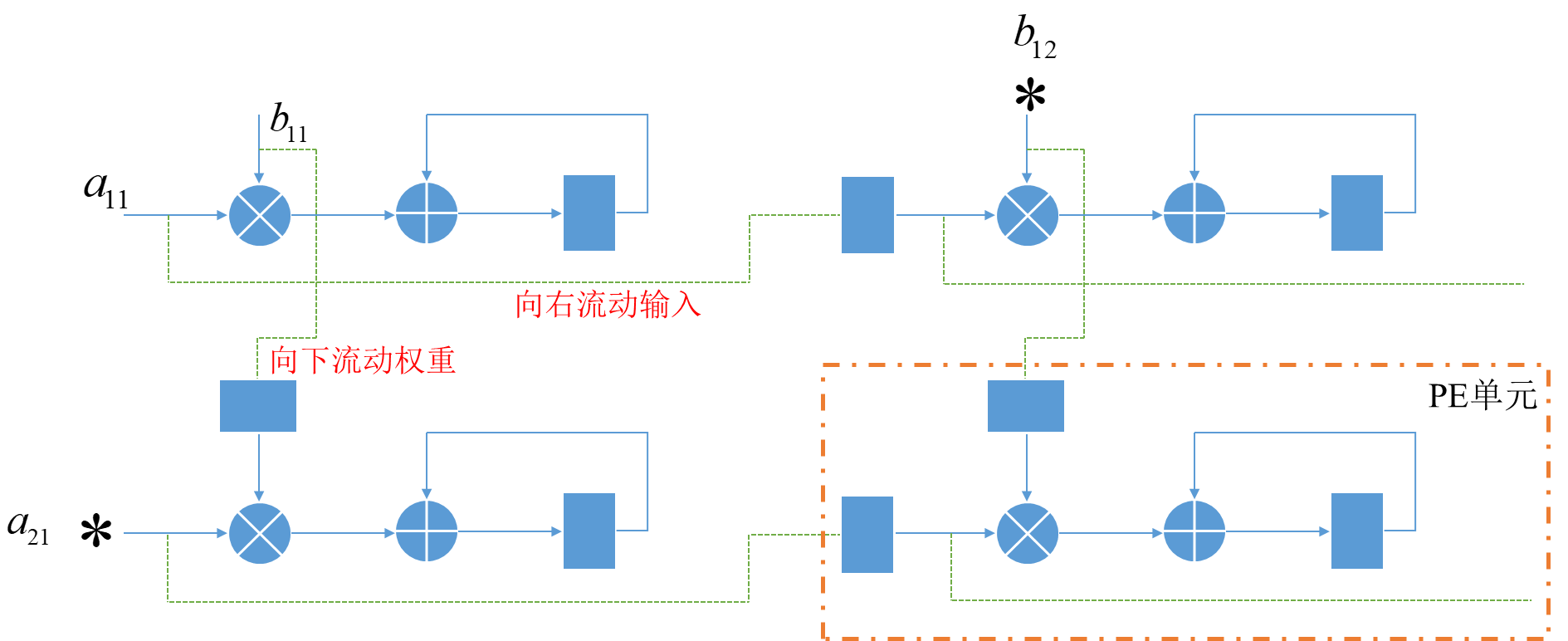
  • 其中*表示延时一拍

• 每个PE单元其实就是一个MAC，通过脉动阵列可以实现在计算的同时将数据同时传导到后面的PE单元

1.2 源文件

• top.v

  module top(
      input clk,
      input rst,
      input en,
      input [4*9-1:0] in1,
      input [4*9-1:0] in2,
      output reg [9*9-1:0] out
      );
  
      reg [3:0] hang1 [0:4];
      reg [3:0] hang2 [0:4];
      reg [3:0] hang3 [0:4];
      reg [3:0] lie1 [0:4];
      reg [3:0] lie2 [0:4];
      reg [3:0] lie3 [0:4];
      reg [3:0] flag;
      wire [3:0] down00,down01,down02,down10,down11,down12,down20,down21,down22;
      wire [3:0] right00,right01,right02,right10,right11,right12,right20,right21,right22;
      wire [7:0] sum00,sum01,sum02,sum10,sum11,sum12,sum20,sum21,sum22;
      reg [3:0] left00;
      reg [3:0] left10;
      reg [3:0] left20;
      reg [3:0] up00;
      reg [3:0] up01;
      reg [3:0] up02;
  
      always@(posedge clk)begin
          if(rst)begin
              out <= 0;
          end
          else begin
              hang1[0] <= in1[3-:4];            //从in1[3]开始向下取4位，即in1[3],in1[2],in1[1],in1[0]，即将in[3:0]赋值给hang1[0]
              hang1[1] <= in1[7-:4];
              hang1[2] <= in1[11-:4];
              hang1[3] <= 4'b0000;
              hang1[4] <= 4'b0000;
              hang2[0] <= 4'b0000;
              hang2[1] <= in1[15-:4];
              hang2[2] <= in1[19-:4];
              hang2[3] <= in1[23-:4];
              hang2[4] <= 4'b0000;
              hang3[0] <= 4'b0000;
              hang3[1] <= 4'b0000;
              hang3[2] <= in1[27-:4];
              hang3[3] <= in1[31-:4];
              hang3[4] <= in1[35-:4];
              lie1[0] <= in2[3-:4];
              lie1[1] <= in2[15-:4];
              lie1[2] <= in2[27-:4];
              lie1[3] <= 4'b0000;
              lie1[4] <= 4'b0000;
              lie2[0] <= 4'b0000;
              lie2[1] <= in2[7-:4];
              lie2[2] <= in2[19-:4];
              lie2[3] <= in2[31-:4];
              lie2[4] <= 4'b0000;
              lie3[0] <= 4'b0000;
              lie3[1] <= 4'b0000;
              lie3[2] <= in2[11-:4];
              lie3[3] <= in2[23-:4];
              lie3[4] <= in2[35-:4];
          end
      end
  
      always@(posedge clk) begin
          if(rst)begin
              flag <= 0;
          end
          else if(en) begin
              //if(flag==4'd5)
                  //flag<=0;
                  //else
              flag <= flag + 1;
          end
      end
  
      always@(posedge clk)begin
          case(flag)
              0 : begin
                  left00 <= hang1[0];
                  left10 <= hang2[0];
                  left20 <= hang3[0];
                  up00 <= lie1[0];
                  up01 <= lie2[0];
                  up02 <= lie3[0];
                  end
              1 : begin
                  left00 <= hang1[1];
                  left10 <= hang2[1];
                  left20 <= hang3[1];
                  up00 <= lie1[1];
                  up01 <= lie2[1];
                  up02 <= lie3[1];
                  end
              2 : begin
                  left00 <= hang1[2];
                  left10 <= hang2[2];
                  left20 <= hang3[2];
                  up00 <= lie1[2];
                  up01 <= lie2[2];
                  up02 <= lie3[2];
                  end
              3 : begin
                  left00 <= hang1[3];
                  left10 <= hang2[3];
                  left20 <= hang3[3];
                  up00 <= lie1[3];
                  up01 <= lie2[3];
                  up02 <= lie3[3];
                  end
              4 : begin
                  left00 <= hang1[4];
                  left10 <= hang2[4];
                  left20 <= hang3[4];
                  up00 <= lie1[4];
                  up01 <= lie2[4];
                  up02 <= lie3[4];
                  end
              default : begin
                  left00 <= 0;
                  left10 <= 0;
                  left20 <= 0;
                  up00 <= 0;
                  up01 <= 0;
                  up02 <= 0;
                  end
          endcase
      end
      
      pe pe00(
          .clk(clk),.rst(rst),.left(left00),.up(up00),.down(down00),.right(right00),.sum_out(sum00)
      );
      pe pe01(
          .clk(clk),.rst(rst),.left(right00),.up(up01),.down(down01),.right(right01),.sum_out(sum01)
      );
      pe pe02(
          .clk(clk),.rst(rst),.left(right01),.up(up02),.down(down02),.right(right02),.sum_out(sum02)
      );
      pe pe10(
          .clk(clk),.rst(rst),.left(left10),.up(down00),.down(down10),.right(right10),.sum_out(sum10)
      );
      pe pe11(
          .clk(clk),.rst(rst),.left(right10),.up(down01),.down(down11),.right(right11),.sum_out(sum11)
      );
      pe pe12(
          .clk(clk),.rst(rst),.left(right11),.up(down02),.down(down12),.right(right12),.sum_out(sum12)
      );
      pe pe20(
          .clk(clk),.rst(rst),.left(left20),.up(down10),.down(down20),.right(right20),.sum_out(sum20)
      );
      pe pe21(
          .clk(clk),.rst(rst),.left(right20),.up(down11),.down(down21),.right(right21),.sum_out(sum21)
      );
      pe pe22(
          .clk(clk),.rst(rst),.left(right21),.up(down12),.down(down22),.right(right22),.sum_out(sum22)
      );
  
  endmodule

• pe.v

  module pe(
      input clk,
      input rst,
      input [3:0] left,
      input [3:0] up,
      output reg [3:0] down,
      output reg [3:0] right,
      output reg [7:0] sum_out,
      wire [7:0] mult_out
      );
  
      always@(posedge clk)begin
          if(rst) begin
              right <= 0;
              down <=0;
              sum_out <= 0;
          end
          else begin
              down <= up;
              right <= left;
              sum_out <= sum_out + mult_out;
          end
      end
  
      multiply u_mult(
          .a(left),
          .b(up),
          .out(mult_out)
      );
  
  endmodule

• multiply.v

  module multiply(
      input [3:0]a,
      input [3:0]b,
      output wire [7:0] out
      );
  
      assign out = a * b;
  
  endmodule

1.3 Testbench

module top_tb();
    reg clk;
    reg rst;
    reg en;
    reg [4*9-1:0] in1;
    reg [4*9-1:0] in2;
    wire [9*9-1:0] out;

    initial begin
        clk=0;
        rst=0;
        in1=0;
        in2=0;
        en=0;
        #10
        rst=1;
        #10
        rst=0;
        in1=36'b0101_0010_0011_0011_0101_0010_0010_0100_0011;
        in2=36'b0101_0010_0011_0011_0101_0010_0010_0100_0011;
        #10
        en=1;
        #100
        $finish;
    end

    always #5 clk=~clk;

    top u_top(
        .clk(clk),
        .rst(rst),
        .in1(in1),
        .in2(in2),
        .out(out),
        .en(en)
        );

endmodule

• 结果如下：

  

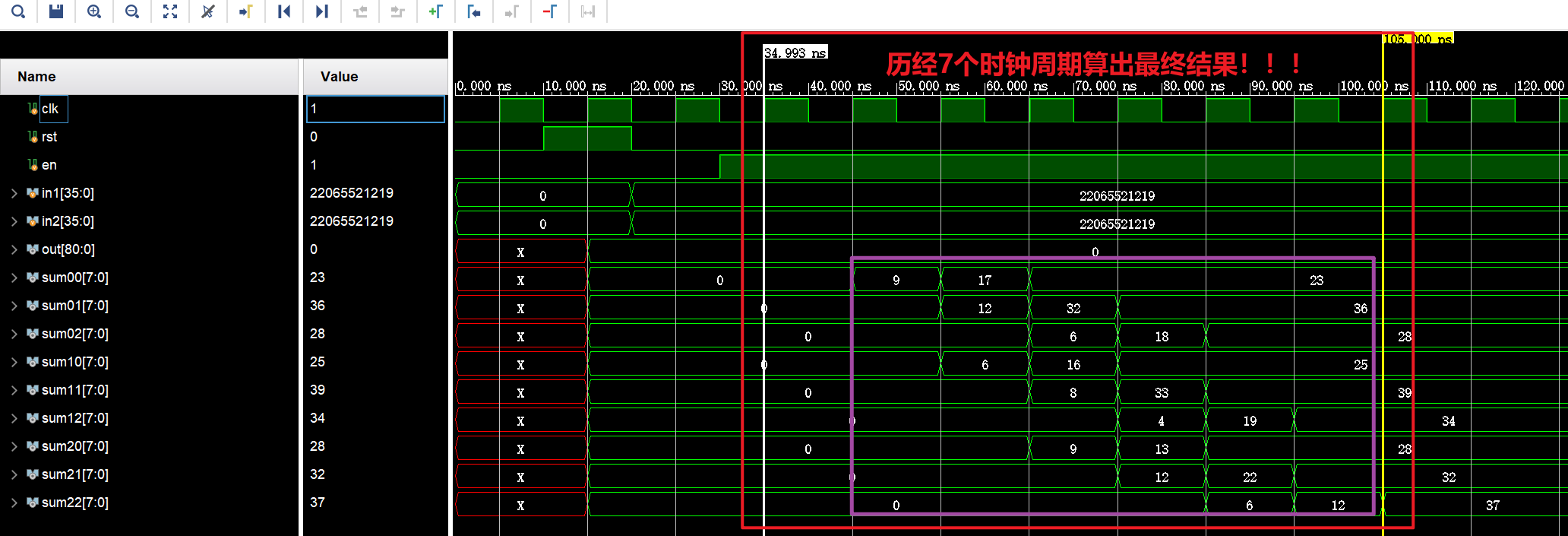
2.模式二：权重存储在脉动阵列单元中

• 在脉动阵列中流动的是输入和权重乘的中间结果，权重存储在脉动计算单元中

2.1 实现思路

• 模式二：脉动阵列计算矩阵乘法的初始状态

  

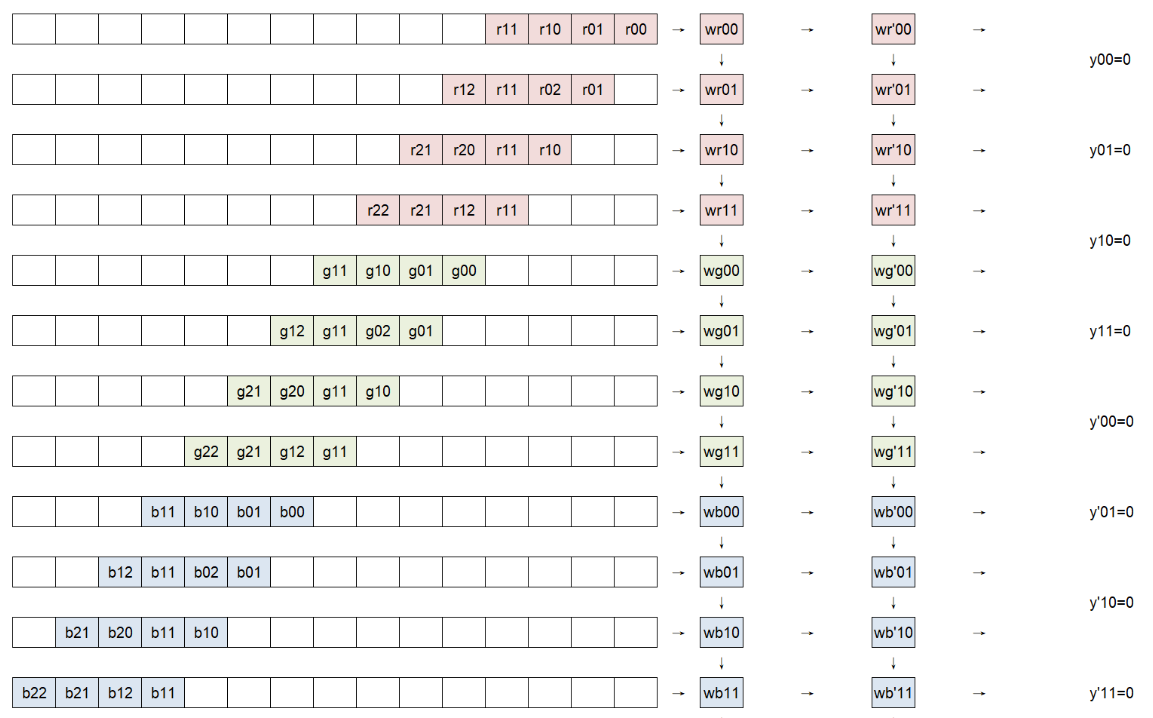
• 实现框架

  

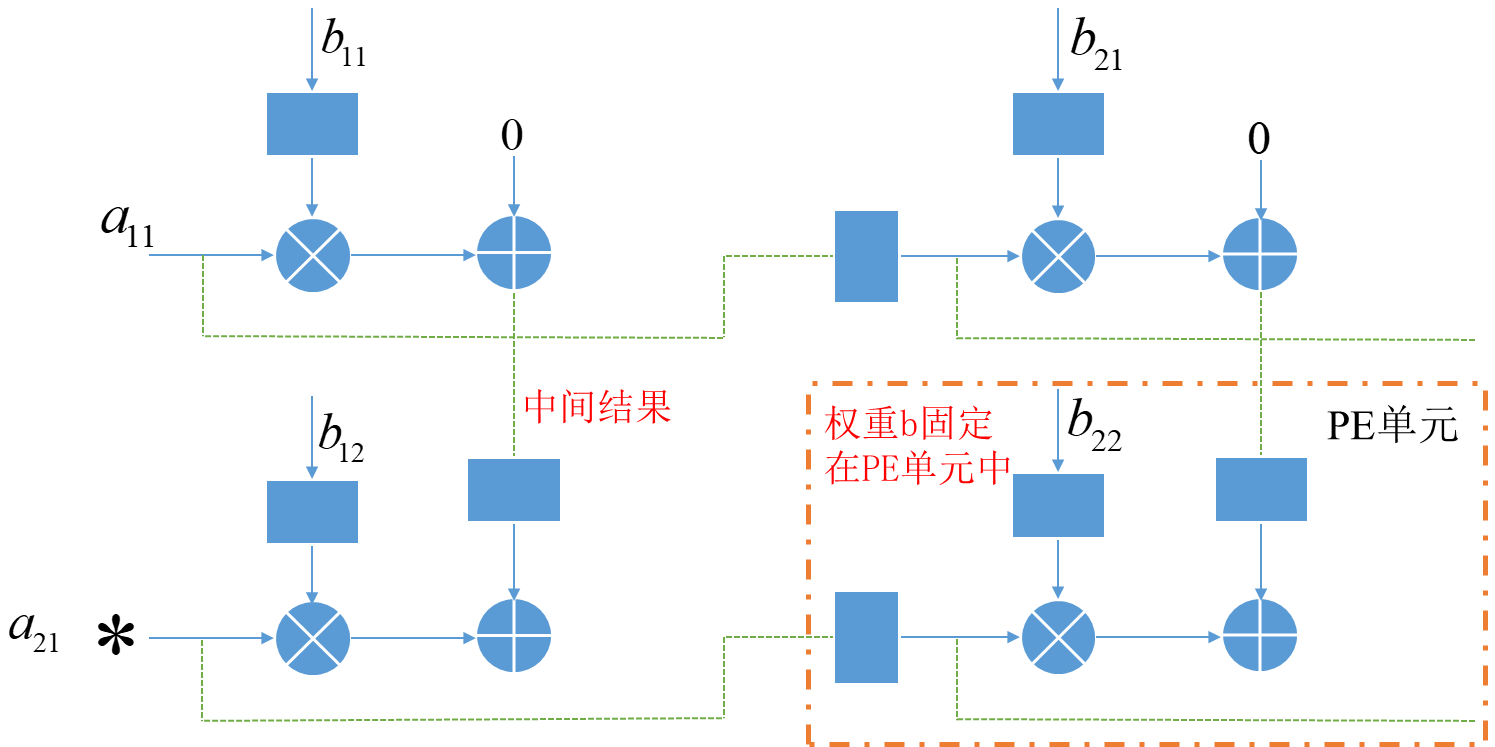
• 这里的话实现的是权重$\times$输入，详情见reference中的参考

  
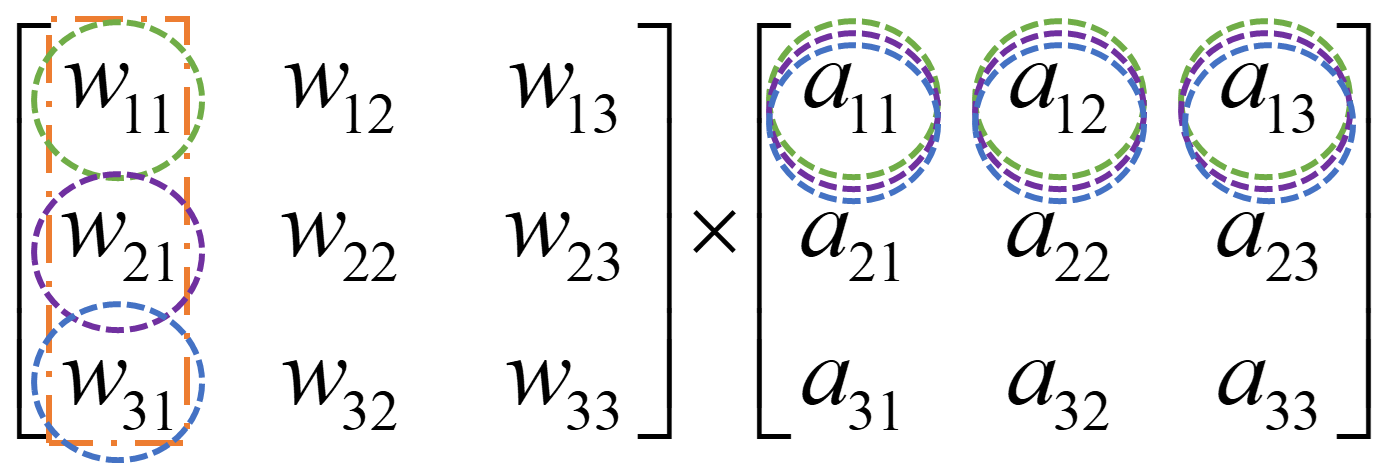
  • 当第一列固定不动的时候，其均只需要分别与$a_{11},a_{12},a_{13}$相乘，故第一列数据$w_{11},w_{21},w_{31}$是作为脉动阵列的第一行的

---

脉动阵列实现卷积操作

• 原理参考：https://hitsz-cslab.gitee.io/dla/lab4/theory/

  

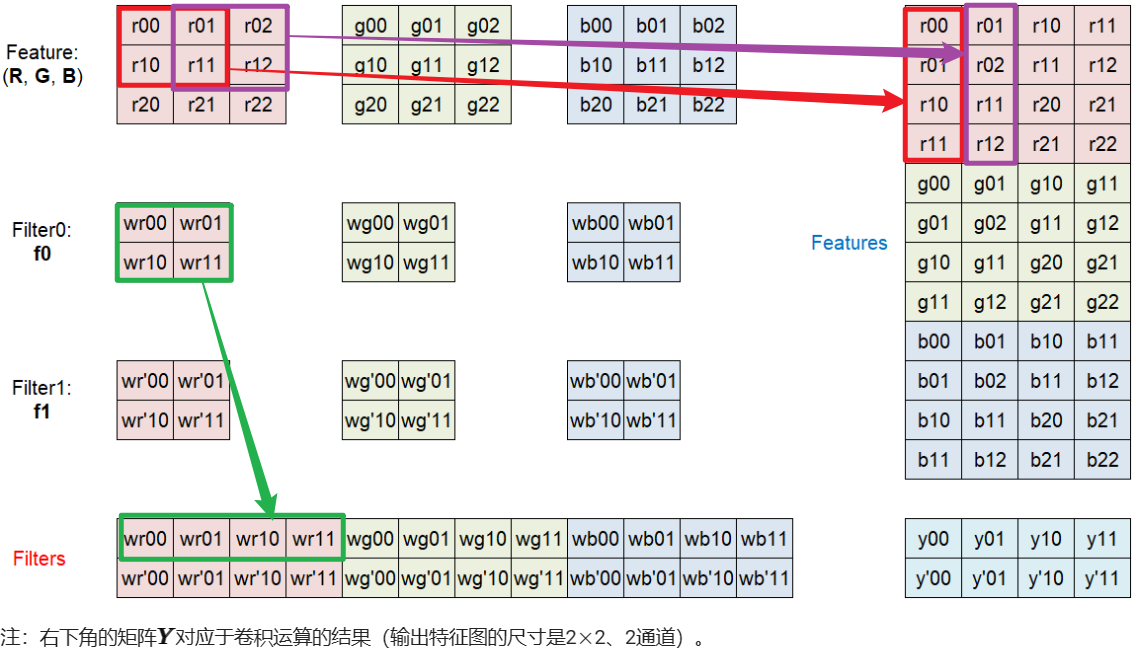
• 将卷积计算进行如上图的转换后即可将卷积计算转化为求矩阵乘法

---

Reference

• 脉动阵列：高性能矩阵乘法器_哔哩哔哩_bilibili

• 实验原理 - 深度学习体系结构（2021秋季） | 哈工大（深圳） (gitee.io)（矩阵乘法模式一和卷积实现看这个就可以理解）

• Google AI芯片TPU核心架构–脉动阵列Systolic Array - 知乎 (zhihu.com)（矩阵乘法模式二的详细解释看这个）

• 脉动阵列实现卷积计算_脉动阵列 卷积-CSDN博客（矩阵乘法模式二看这个，里面有作者手画的图，一看就懂）

• [SystolicArray-2D-FP16/0 Source/PE_Array_2D.sv at main · SuperLiaoXH/SystolicArray-2D-FP16 · GitHub](https://github.com/SuperLiaoXH/SystolicArray-2D-FP16/blob/main/0 Source/PE_Array_2D.sv)

• https://www.cnblogs.com/kongchung/p/13227256.html

• systolic-array-matrix-multiplier/scr/matrix_mul_sa_pipe.v at master · wzc810049078/systolic-array-matrix-multiplier · GitHub