本节主要介绍了高速度结构设计的基本方法，分别从高流量、低时滞、时序等三方面进行了优化

高速度结构设计的基本概念

速度有三种基本定义：
- 流量（Throughput）：定义为每个时钟周期处理的数据量，流量通常的度量是每秒的位数
- 时滞（Latency）：定义为数据输入与处理的数据输出之间的时间，时滞的一般度量是时间或时钟周期
- 时序（Timing）：定义为时序元件之间的逻辑延时，当一个设计没有“满足时序”时，意味着关键路径的延时，即触发器之间的最大延时比预定的时钟周期大
高流量结构使设计每秒可以处理的位数最大化
低时滞结构使一个模块输入端到输出端的延时最小化
时序优化可减少关键组合的路径延时

高流量

高流量设计是与稳定状态数据率有关的设计，高流量设计的概念是流水线（pipeline）
从算法的观点看，在流水线设计中一个重要的概念是“拆开环路”
考虑以下一段代码，它类似于在软件实现求X的三次幂中使用的代码
1
2
3
XPower = 1;
for(int i = 0; i < 3; i++)
XPower = X * XPower;

用Verilog语言实现X三次幂的算法（没有考虑输出范围）

module pipeline_design(
    input clk,start,
    input [7:0] x,
    output reg [7:0] XPower,
    output finished
    );

    reg [7:0] ncount;

    assign finished = (ncount == 0);

    always @(posedge clk) begin
        if(start) begin
            ncount <= 2;
            XPower <= x;
        end
        else if(!finished) begin
            ncount <= ncount - 1;
            XPower <= XPower * x;
        end
    end
endmodule

RTL原理图：
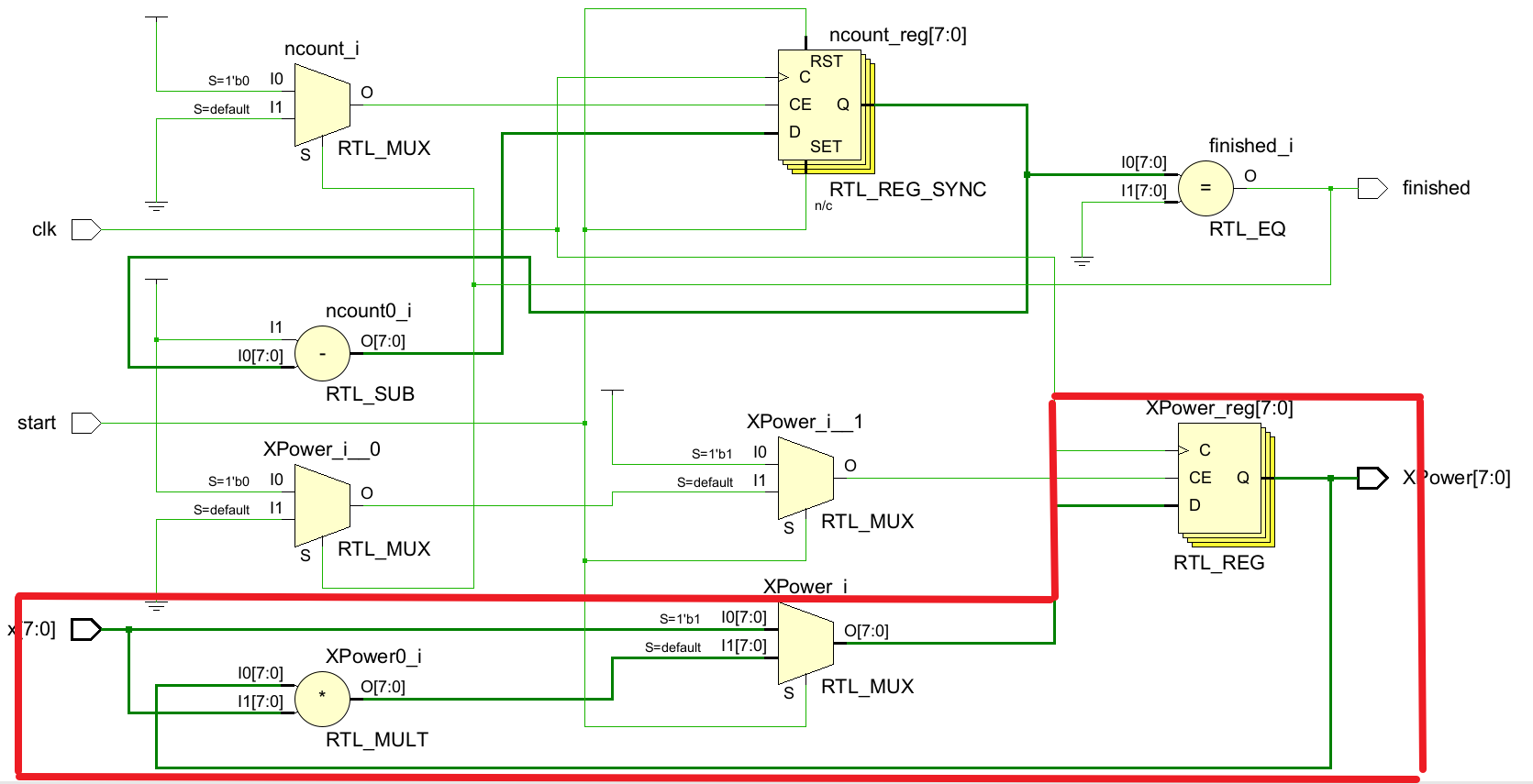
观察被红色圈起来关于x的计算部分：XPower_reg寄存器一直在被重复使用，由于这类迭代实现，新的计算直到前面的计算已经完成才开始。、
这个迭代方法类似于软件实现，也应注意，要求某些握手信号来表示开始和完成一次计算，外部模块也必须利用这个握手信号来传递新数据到模块并接收一个完成的计算
这个迭代实现的性能：
- 流量=8/3，或2.7bit/时钟
- 时滞=3时钟
- 时序=关键路径中一个乘法器延时

流水线版本实现x三次方（没有考虑输出范围）：

module pipeline_design(
    input clk,
    input [7:0] x,
    output reg [7:0] XPower
    );

    reg [7:0] xpower1,xpower2;
    reg [7:0] x1,x2;

    //pipeline 1
    always @(posedge clk) begin
        x1 <= x;
        xpower1 <= x;
    end

    //pipeline 2
    always @(posedge clk) begin
        x2 <= x1;
        xpower2 <= x1 * xpower1;
    end

    //pipepline 3
    always @(posedge clk) begin
        XPower <= x2 * xpower2;
    end
endmodule

RTL原理图：
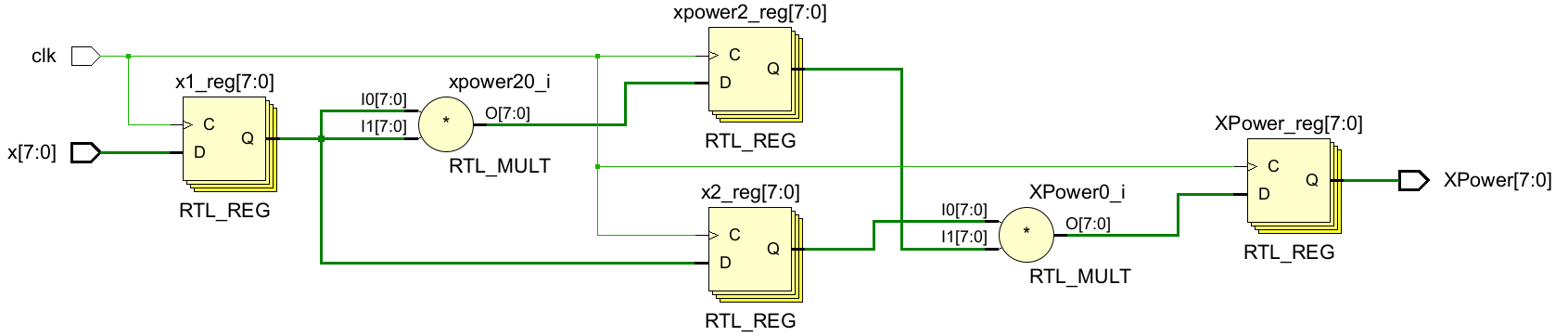
其实实现x的三次方计算，就是要进行两次乘法，于是用三层寄存器将两个乘法器隔开，这样每个乘法器都可以独立干自己的事情，而不受其他级的影响（这里我觉得第一级的寄存器可以不加，只是单纯的进行了一个赋值操作）
$x^3$的最后计算和$x$下一数值的第一次计算二者同时进行
这个流水线设计的性能：
- 流量=8/1 或8位/时钟
- 时滞=3个时钟
- 时序=关键路径中的一个乘法器延时

通常，如果要求将n次迭代环路的算法拆开后，流水线实现将呈现n倍的流量性能增加，拆开一个迭代环路的代价是成比例地增加面积

低时滞

低时滞设计是通过最小化中间处理的延时来尽可能快速地把数据从输入端传递到输出端的设计
去除流水线寄存器可以使输入到输出时序最小化

x三次方算法低时滞实现

module pipepline_design(
    input [7:0] x,
    output reg [7:0] XPower    
    );

    reg [7:0] xpower1,xpower2;
    reg [7:0] x1,x2;

    //pipeline 1
    always @(*) begin
        x1 <= x;
        xpower1 <= x;
    end

    //pipeline 2
    always @(*) begin
        x2 <= x1;
        xpower2 <= x1 * xpower1;
    end

    //pipepline 3
    always @(*) begin
        XPower <= x2 * xpower2;
    end
endmodule

RTL原理图
在上面的例子中，寄存器从流水线中分离出去，每一级都是前级的组合表达式
这个低时滞实现的性能为：
- 流量=8位/时钟（假设每个时钟一个新的输入）
- 时滞=在1和2个乘法器延时之间
- 时序=关键路径中2个乘法器延时

可以通过移去流水线寄存器来减少时滞，但这一操作会增加寄存器之间的组合延时

时序

时序指的是一个设计的时钟速度，在设计中任何两个时序元件之间的最大延时将决定最大的时钟速度
最高速度或最大频率可以直接按照著名的最大频率方程定义：
$$
F_{max}=\frac{1}{T_{clk-q}+T_{logic}+T_{routing}+T_{setup}-T_{skew}}
$$
- $T_{clk-q}$是从时钟到达直至数据到达$Q$端的时间，$T_{logic}$是逻辑通过触发器之间的传播延时，$T_{routing}$是触发器之间的布线延时，$T_{setup}$是下一个时钟上升沿之前数据必须到达$D$端的最小时间（建立时间），$T_{skew}$是启动触发器和捕捉触发器之间时钟的传播延时

1.添加寄存器层次

该策略是添加中间的寄存器层次到关键路径，这个技术应该利用在高速流水线的设计
其核心思想是：把关键路径分成两个更小延时的路径，添加寄存器层次改进时序

假设以下有限脉冲响应（FIR）实现的结构不满足时序要求：

module pipeline_design(
    input clk,
    input validsample,
    input [7:0] A, B, C, X,
    output reg [7:0] Y
    );
    
    reg [7:0] X1,X2;

    always @(posedge clk) begin
        if(validsample) begin
            X1 <= X;
            X2 <= X1;
            Y <= A * X + B * X1 + C * X2;
        end
    end
endmodule

RTL原理图
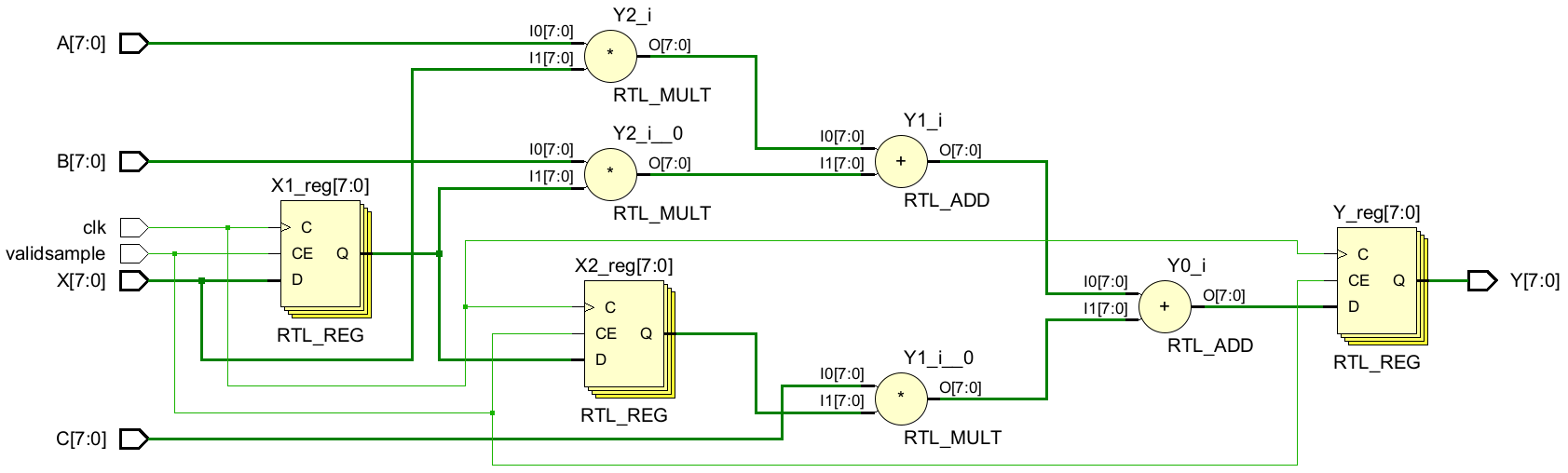
所有乘/加操作发生在一个时钟周期，换而言之，一个乘法器和一个加法器组成的关键路径比最小时钟周期的要求大

在乘法器和加法器之间添加一个流水线层次

module pipeline_design(
    input clk,
    input validsample,
    input [7:0] A, B, C, X,
    output reg [7:0] Y
    );
    
    reg [7:0] X1,X2;
    reg [7:0] mul1, mul2, mul3;
    
    always @(posedge clk) begin
        if(validsample) begin
            X1 <= X;
            X2 <= X1;
            mul1 <= A * X;
            mul2 <= B * X1;
            mul3 <= C * X2;
        end
    end

    always @(posedge clk) begin
        Y <= mul1 + mul2 + mul3;
    end
endmodule

RTL原理图

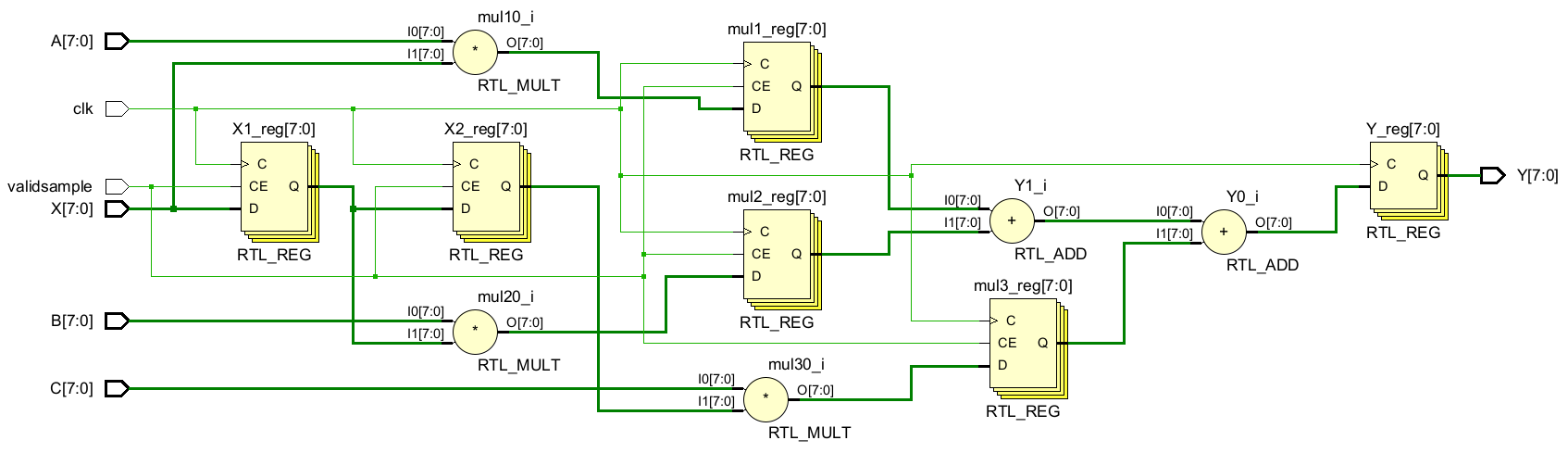
2.并行结构

该策略是重新组织关键路径，以致并行地实现逻辑结构。当通过一列串联的逻辑计算函数可以分解和并行时，就应该利用该技术
其核心思想是：把一个逻辑功能分为大量可以并行计算的更小的功能，减少路径延时为子结构的最小延时
假设在高流量一节设计的三级流水线不满足时序的要求，位了产生并行结构，可以将乘法器分解成独立的操作，重新组合它们。例如，一个8位的二进制乘法器可以用字段A和B表示：
$$
X=\{A,B\}
$$
- 其中$A$是最高有效位字段，$B$是最低有效位字段
- 因为在3次幂的例子中被乘数等于乘数，乘数操作可以重新组织如下：
  $$
  X\times X=\{A,B\}\times \{A,B\} = \{(A\times A),(2\times A \times B),(B\times B)\}
  $$
- 这样就把问题简化为一个串行的4位乘法器，然后重新组合乘积

可以用以下模块实现：

module pipeline_design(
    input clk,
    input [7:0] x,
    output [7:0] XPower
    );

    reg [7:0] xpower1;
    wire [7:0] xpower2;
    reg [3:0] xpower2_ppAA, xpower2_ppAB, xpower2_ppBB;
    reg [3:0] xpower3_ppAA, xpower3_ppAB, xpower3_ppBB;
    reg [7:0] x1,x2;

    wire [3:0] xpower1_A = xpower1[7:4];
    wire [3:0] xpower1_B = xpower1[3:0];

    wire [3:0] x1_A = x1[7:4];
    wire [3:0] x1_B = x1[3:0];

    wire [3:0] xpower2_A = xpower2[7:4];
    wire [3:0] xpower2_B = xpower2[3:0];

    wire [3:0] x2_A = x2[7:4];
    wire [3:0] x2_B = x2[3:0];

    //pipeline 1
    always @(posedge clk) begin
        x1 <= x;
        xpower1 <= x;
    end

    //pipeline 2
    always @(posedge clk) begin
        x2 <= x1;
        xpower2_ppAA <= xpower1_A * x1_A;
        xpower2_ppAB <= xpower1_A * x1_B;
        xpower2_ppBB <= xpower1_B * x1_B;
    end

    //pipepline 3
    always @(posedge clk) begin
        xpower3_ppAA <= xpower2_A * x2_A;
        xpower3_ppAB <= xpower2_A * x2_B;
        xpower3_ppBB <= xpower2_B * x2_B;
    end

    assign xpower2 = (xpower2_ppAA << 8) + (2 * xpower2_ppAB << 4) + xpower2_ppBB;
    assign XPower = (xpower3_ppAA << 8) + (2 * xpower3_ppAB << 4) + xpower3_ppBB;

endmodule

RTL的部分原理图
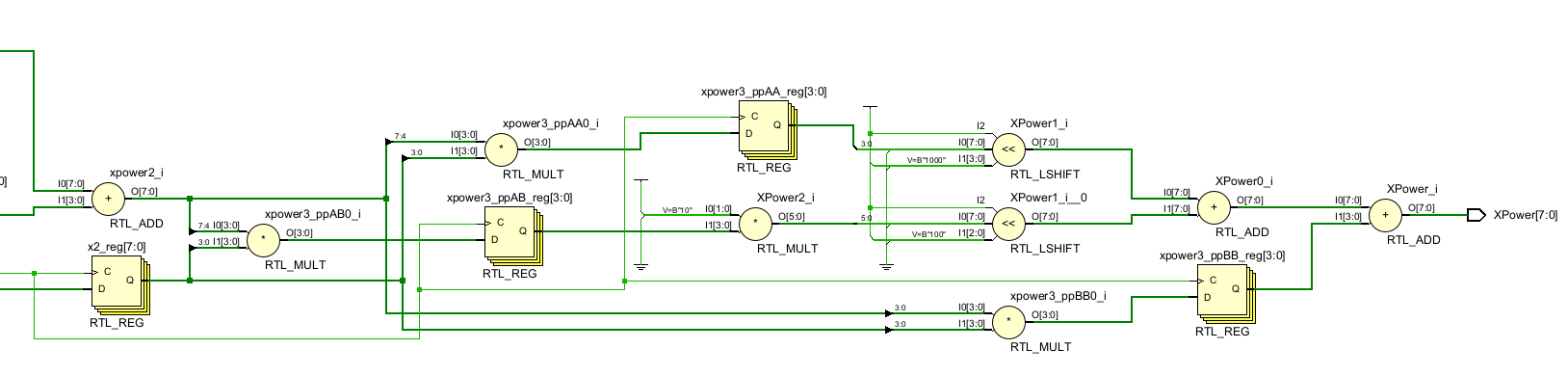
这个设计没有考虑任何溢出的问题，只是用来说明要点，乘法器可以拆分成能够独立操作的更小的功能
通过把乘法器拆成可以并行执行的更小的操作，最大的延时可以减小到通过任何子结构的最长延时

3.展开逻辑结构

该策略的核心是：去除不需要的特权编码（我的理解是写verilog时没有必要的优先级结构），展平逻辑结构，减少路径延时

考虑下面地址译码器，其用于写入4个寄存器的控制信号：

module pipeline_design(
    input clk,in,
    input [3:0] ctrl,
    output reg [3:0] rout
    );

    always @(posedge clk) begin
        if(ctrl[0]) begin
            rout[0] = in;
        end 
        else if (ctrl[1]) begin
            rout[1] = in;
        end
        else if (ctrl[2]) begin
            rout[2] = in;
        end
        else if (ctrl[3]) begin
            rout[3] = in;
        end
    end

endmodule

RTL原理图：
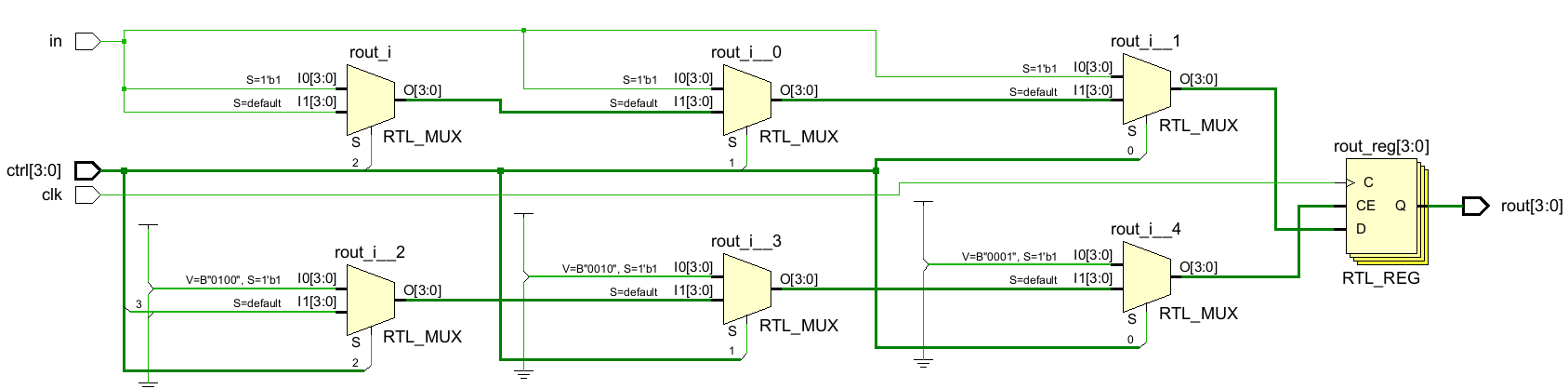
如果控制线是来自另一个模块地址译码器的选通，那么每个选通对于其他的选通是相互排斥的，因为它们都代表唯一的地址，所以这个模块中就不需要带有优先级的方式（用一堆if else判断，这会增加电路的延时）去编写代码

为了去除此特权，展平此逻辑，可以按照如下方式给这个模块编码：

module pipeline_design(
    input clk,in,
    input [3:0] ctrl,
    output reg [3:0] rout
    );

    always @(posedge clk) begin
        if(ctrl[0]) begin
            rout[0] = in;
        end 
        if (ctrl[1]) begin
            rout[1] = in;
        end
        if (ctrl[2]) begin
            rout[2] = in;
        end
        if (ctrl[3]) begin
            rout[3] = in;
        end
    end

endmodule

RTL原理图

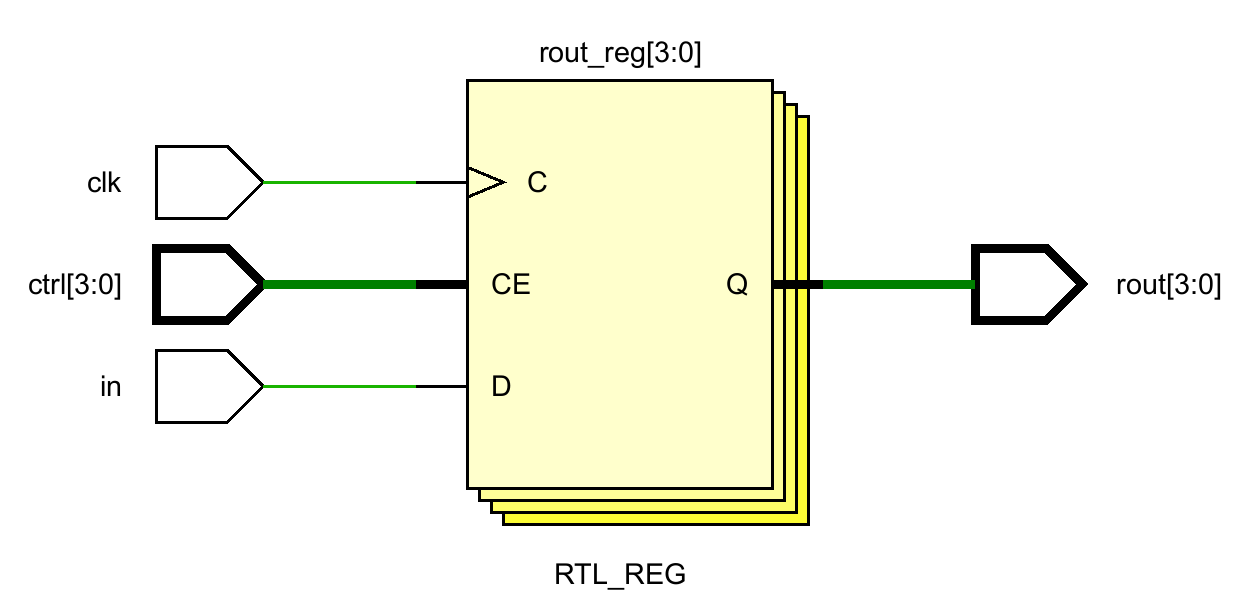
（20240604）附：第一次知道原来一个always中多个if并行，编译器不会编译成多个mux并行（针对在多个if中对同一个变量赋值的情况），还是级联的mux，最后一个if的优先级最高（越靠近输出）
可参考：Verilog中单if语句、多if语句和case语句与优先级的关系_verilog if else if 执行顺序-CSDN博客

我当时是测试了这样一段代码：

always @(posedge clk) begin
    begin
        if(cfar_flag[0]) begin
            object <= 1'b1;
        end      
        if(cfar_flag[1]) begin
            object <= 1'b1;
        end  
        if(cfar_flag[2]) begin
            object <= 1'b1;
        end  
        if(cfar_flag[3]) begin
            object <= 1'b1;
        end
        if(cfar_flag[4]) begin
            object <= 1'b1;
        end      
        if(cfar_flag[5]) begin
            object <= 1'b1;
        end  
        if(cfar_flag[6]) begin
            object <= 1'b1;
        end  
        if(cfar_flag[7]) begin
            object <= 1'b1;
        end     
    end
end

综合结果：（圈起来的优先级最高cfar_flag[7]）

如果把if放在不同always中，那么就会综合出并行的效果：

genvar i;
generate
    for(i = 0; i < 8; i = i + 1) begin
        always @(posedge clk) begin
            if(cfar_flag[i]) begin
                object <= 2'd2;
            end        
        end
    end
endgenerate

综合结果：

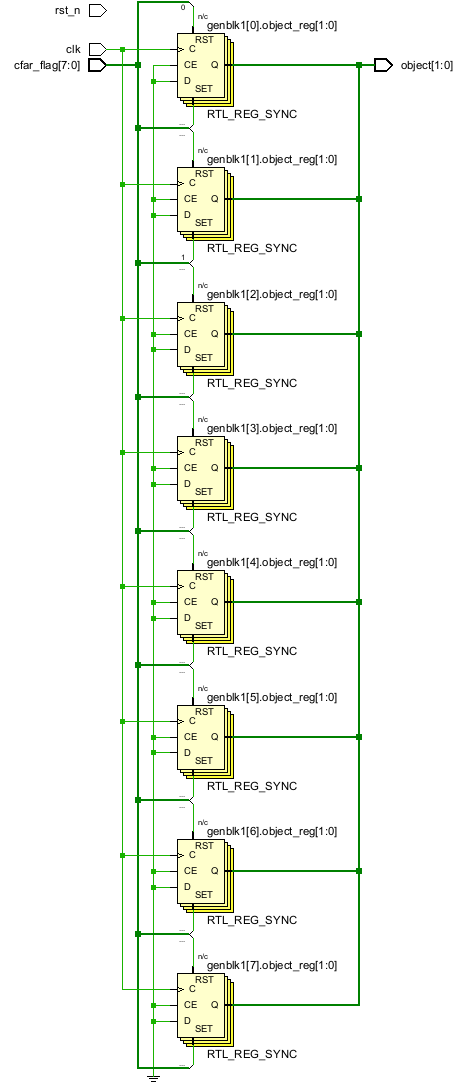
4.寄存器平衡

该策略是平等地重新分布寄存器之间的逻辑，减少任何两个寄存器之间最坏条件的延时（我的理解是有的两个寄存器之间的组合延时很长，有的很短，所以需要均分一下）
其核心是：从关键路径移动组合逻辑到相邻路径，寄存器平衡改善时序

对于以下代码描述的3个8位输入的加法器

module pipeline_design(
    input clk,
    input [7:0] A, B, C,
    output reg [7:0] sum
    );

    reg [7:0] rA, rB, rC;

    //pipeline 1
    always @(posedge clk) begin
        rA <= A;
        rB <= B;
        rC <= C;
    end

    //pipeline 2
    always @(posedge clk) begin
        sum <= rA + rB + rC;
    end
endmodule

RTL原理图：
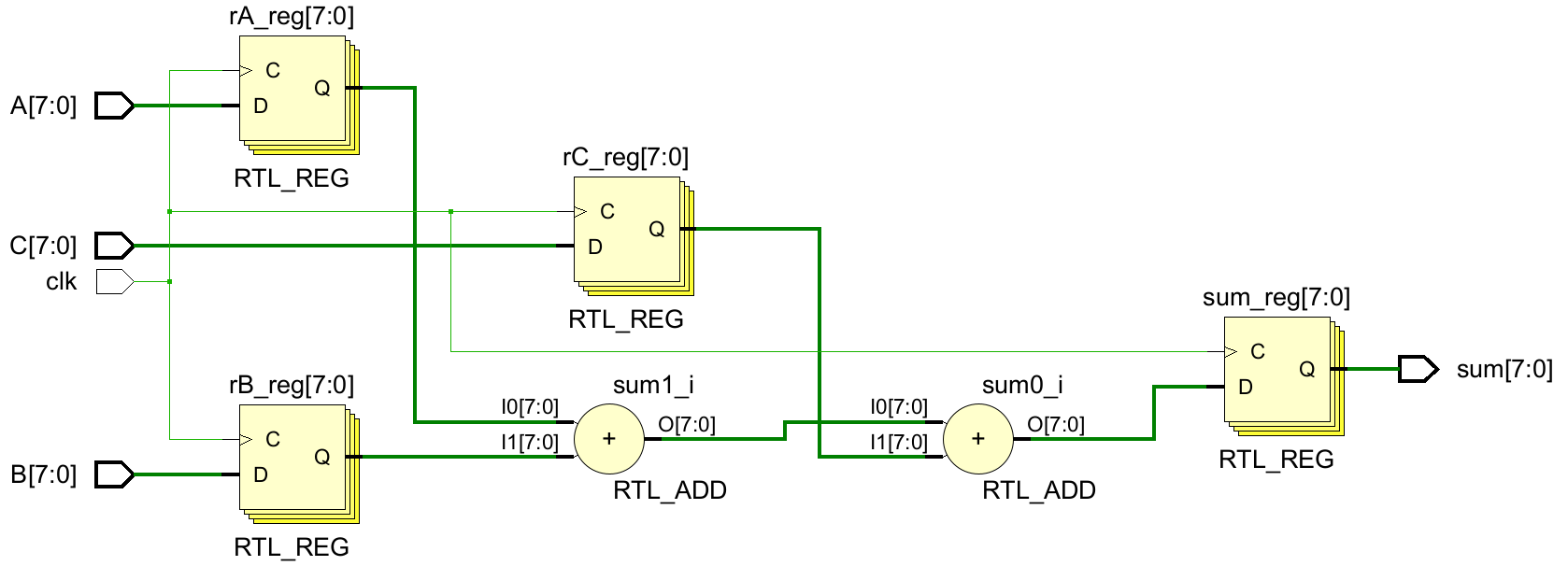
第一个寄存器级是由$rA,rB,rC$组成的，第二级由$sum$组成级1和级2之间的逻辑是全部输入的加法器，但是输入与第一个寄存器之间不包含逻辑

如果通过加法器定义关键路径，在关键路径中的一些逻辑可以移回到第一级，以平衡在两个寄存器级之间的逻辑负载，做出以下修改：

module pipeline_design(
    input clk,
    input [7:0] A, B, C,
    output reg [7:0] sum
    );

    reg [7:0] rABsum, rC;

    //pipeline 1
    always @(posedge clk) begin
        rABsum <= A + B;
        rC <= C;
    end

    //pipeline 2
    always @(posedge clk) begin
        sum <= rABsum + rC;
    end
endmodule

RTL原理图：
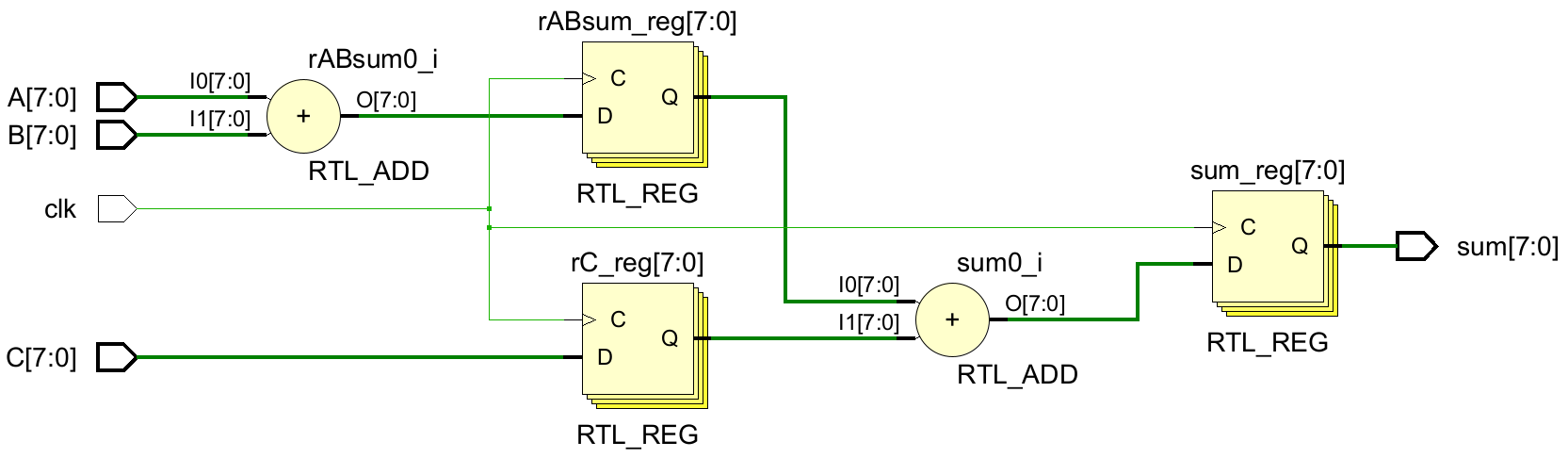
现在输入与第一个寄存器之间移回一个加法操作，这样平衡流水线级之间的逻辑，缩短了关键路径

5.重新安排路径

该策略是在数据流中重新安排路径使关键路径最小化。当多个路径与关键路径组合时应该利用该技术

考虑以下的模块：

module pipeline_design(
    input clk,
    input [7:0] A, B, C,
    input Cond1, Cond2,
    output reg [7:0] Out
    );

    always @(posedge clk) begin
        if(Cond1) begin
            Out <= A;
        end 
        else if(Cond2 && (C < 8)) begin
            Out <= B;
        end
        else begin
            Out <= C;
        end
    end
endmodule

RTL原理图：

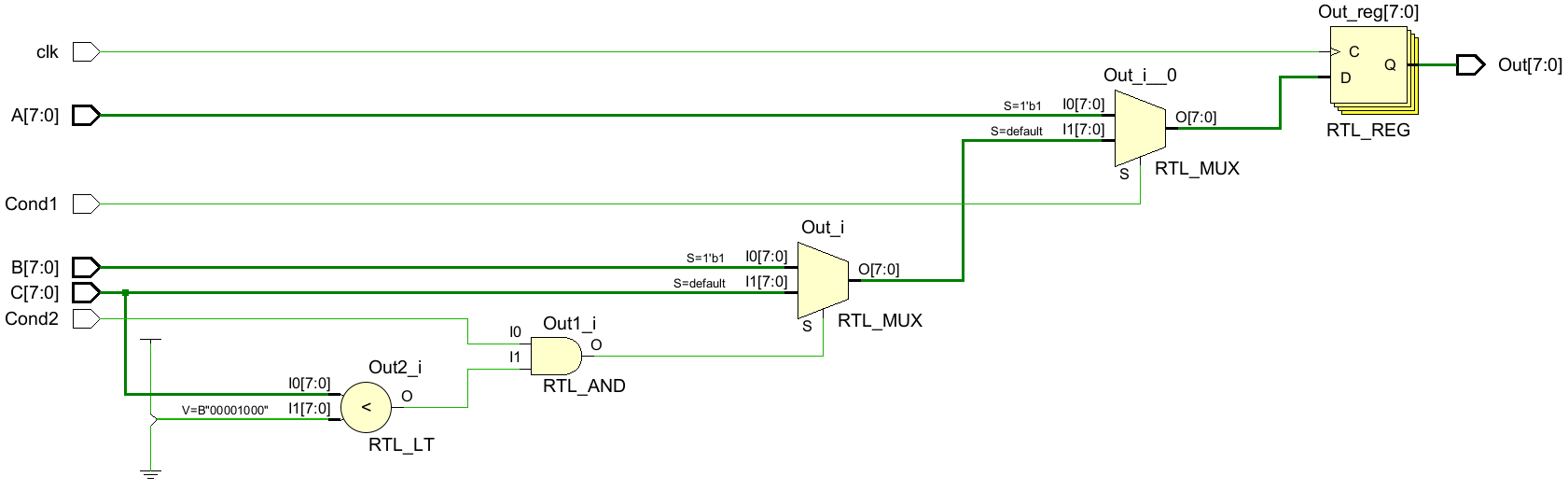
重新组织代码后：

module pipeline_design(
    input clk,
    input [7:0] A, B, C,
    input Cond1, Cond2,
    output reg [7:0] Out
    );

    wire CondB;
    assign CondB = (Cond2 & !Cond1);

    always @(posedge clk) begin
        if(CondB && (C < 8)) begin
            Out <= B;
        end 
        else if(Cond1) begin
            Out <= A;
        end
        else begin
            Out <= C;
        end
    end
endmodule

RTL原理图：
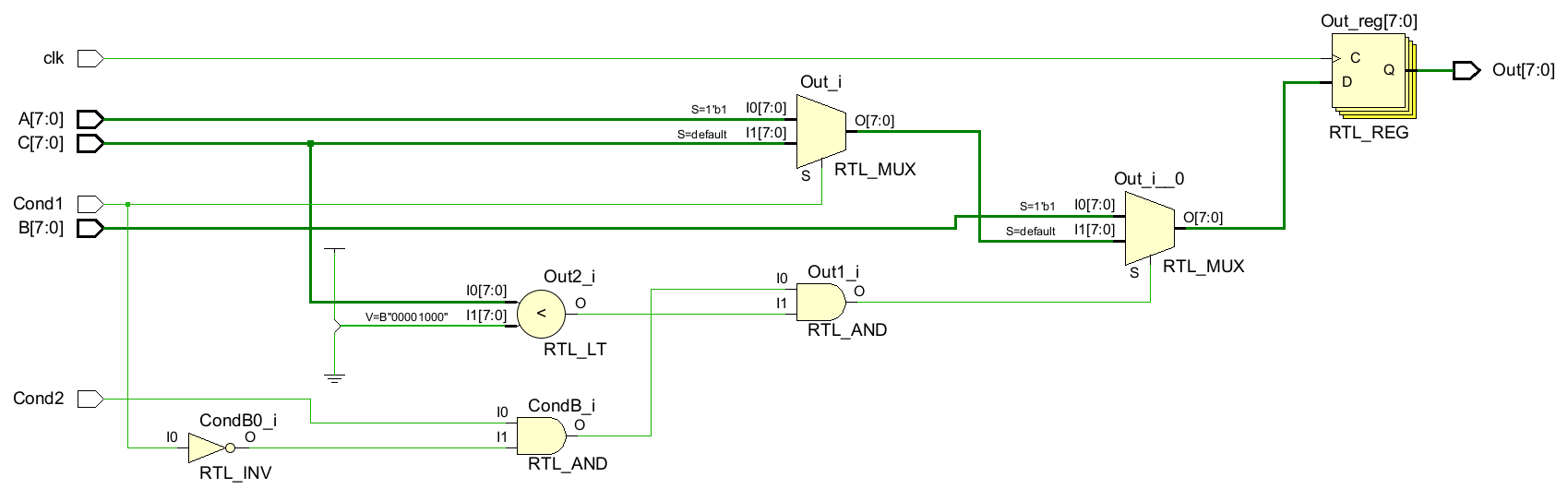
由于重新组织代码，已经从与MUX串联的关键路径移去一个门

因此要特别注意，实际的函数是如何编码的，这对时序性能有直接的影响

ssy的小天地

FPGA数字信号处理之高速度结构设计