本节主要介绍了常见的加法器与乘法器的加速设计方法
加法器
1.Ripple Carry Adder（串行逐个进位加法器）
Ripple Carry Adder就是串联加法器，前一个加法器的进位会连接到下一个加法器的进位输入
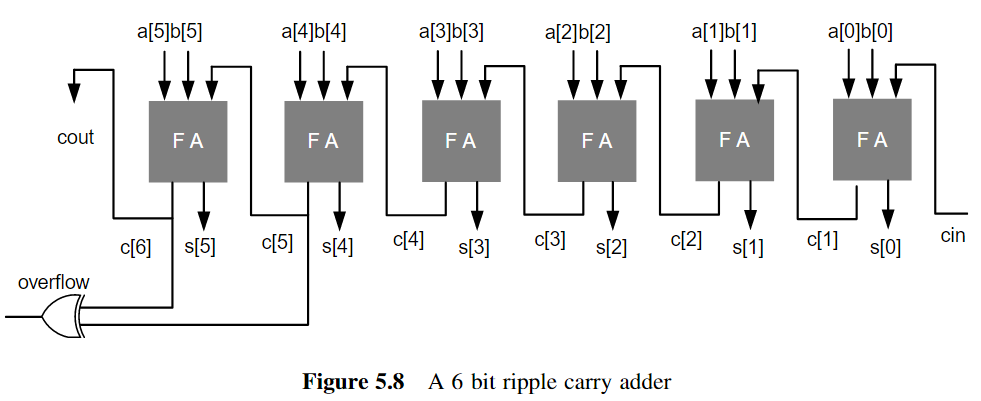
Ripple Carry Adder的关键路径延迟为：
$$
T_{RCA}=(N-1)T_{FA}+T_m
$$- $T_{FA}$是全加器的延时，$T_{m}$是全加器进位产生的延迟
ripple_carry_adder.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23module ripple_carry_adder #(parameter W=16) (
input clk,
input [W-1:0] a, b,
input cin,
output reg [W-1:0] s_r,
output reg cout_r
);
wire [W-1:0] s;
wire cout;
reg [W-1:0] a_r, b_r;
reg cin_r;
assign {cout,s} = a_r + b_r + cin_r;
always@(posedge clk) begin
a_r<=a;
b_r<=b;
cin_r<=cin;
s_r<=s;
cout_r<=cout;
end
endmodule原理图如下：
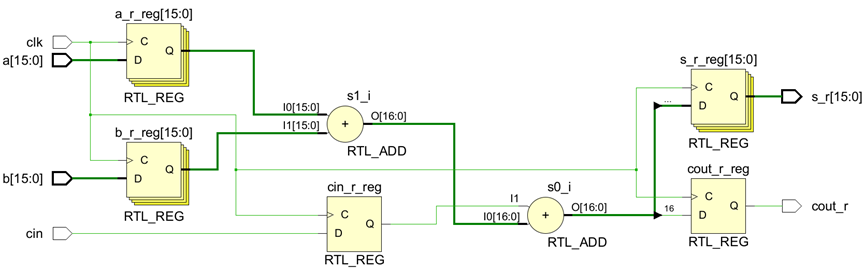
2.Carry Look-ahead Adder（超前进位加法器）
对于Ripple Carry Adder加法器，就4位加法器算法而言，在最坏情况下，做一次加法运算需要经过4个全加器的传输时间才能得到最终运算结果，运算的延时主要是由于进位的延迟引起的，为了提高运算速度，必须尽量减小由于进位信号逐级传递所耗费的时间
Carry Look-ahead Adder（CLA）可以有效的解决这一问题
进位输出位方程：
$$
c_{i+1}=a_i\cdot b_i+c_i\cdot(a_i\bigoplus b_i)
$$- $\bigoplus $代表异或，$\cdot$代表与门
其中，进位产生项$g_i$：
$$
g_i=a_i\cdot b_i
$$进位传播项$p_i$：
$$
p_i=a_i \bigoplus b_i
$$则$c_{i+1}$：
$$
c_{i+1}=g_i+c_i\cdot p_i
$$而输出结果位$s_i$：
$$
s_i=p_i\bigoplus c_i
$$
故CLA的主要思想是先对每位计算$g_i$和$p_i$的值，然后运用它们来计算进位$c_{i+1}$和$s_i$，这避免了进位串行传播通过进位链，从而实现超前进位的目的
一般是构建4bit的CLA，否则资源占用会过大：
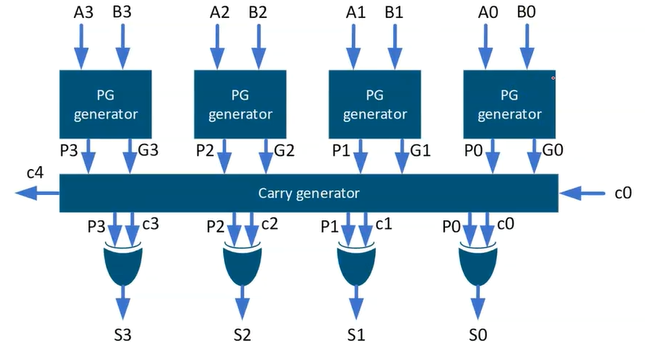
这里给出位数可变的通用CLA的设计文件BinaryCarryLookaheadAdder.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38module BinaryCarryLookaheadAdder # (parameter N=16)(
input [N-1:0] a,b,
input c_in,
output reg [N-1:0] sum,
output reg c_out
);
reg [N-1:0] p, g, P, G;
reg [N:0] c;
integer i;
always @(*) begin
for (i=0;i<N;i=i+1) begin // Generate all ps and gs
p[i] = a[i] ^ b[i];
g[i] = a[i] & b[i];
end
end
always @(*) begin
// Linearly apply dot operators
P[0] = p[0];
G[0] = g[0];
for (i=1; i<N; i=i+1) begin
P[i] = p[i] & P[i-1];
G[i] = g[i] | (p[i] & G[i-1]) ;
end
end
always@(*) begin //Generate all carries and sum
c[0] = c_in;
for(i=0;i<N;i=i+1) begin
c[i+1] = G[i] | (P[i] & c[0]);
sum[i] = p[i] ^ c[i];
end
c_out = c[N];
end
endmoduleCarry Select Adder采用面积换速度的思想，由于进位不确定导致下一级加法器只能等待，反正进位不是0就是1，那么可以提前算出1或者0的情况，最后再由进位去选择算好的结果
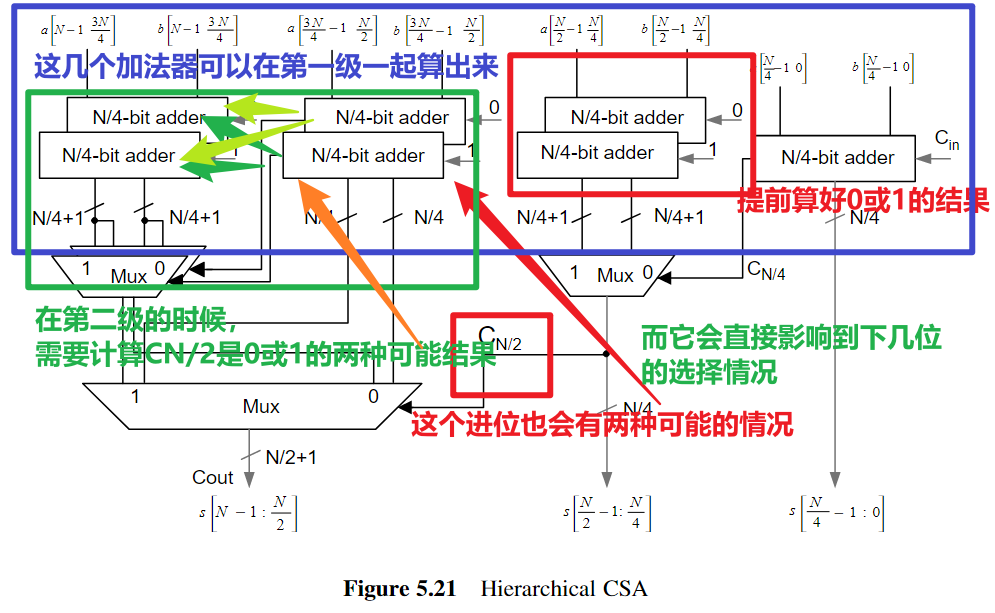
- 图中所说的第二级其实只是做了MUX的判断，具体需要结合代码分析理解
HierarchicalCSA.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35module HierarchicalCSA(a, b, cin, sum, c_out);
input [15:0] a,b;
input cin;
output c_out;
output [15:0] sum;
wire c4, c8, c8_0, c8_1, c12_0, c12_1, c16_0, c16_1, c16L2_0, c16L2_1;
wire [15:4] sumL1_0, sumL1_1;
wire [15:12] sumL2_0, sumL2_1;
// Level one of hierarchical CSA
assign {c4,sum[3:0]} = a[3:0] + b[3:0] + cin;
assign {c8_0, sumL1_0[7:4]} = a[7:4] + b[7:4] + 1'b0;
assign {c8_1, sumL1_1[7:4]} = a[7:4] + b[7:4] + 1'b1;
assign {c12_0,sumL1_0[11:8]} = a[11:8] + b[11:8] + 1'b0;
assign {c12_1,sumL1_1[11:8]} = a[11:8] + b[11:8] + 1'b1;
assign {c16_0, sumL1_0[15:12]} = a[15:12] + b[15:12] + 1'b0;
assign {c16_1, sumL1_1[15:12]} = a[15:12] + b[15:12] + 1'b1;
// Level two of hierarchical CSA
assign c8 = c4 ? c8_1 : c8_0;
assign sum[7:4] = c4 ? sumL1_1[7:4]: sumL1_0[7:4];
// Selecting sum and carry within a group
assign c16L2_0 = c12_0 ? c16_1 : c16_0;
assign sumL2_0[15:12] = c12_0 ? sumL1_1[15:12] : sumL1_0[15:12];
assign c16L2_1 = c12_1 ? c16_1 : c16_0;
assign sumL2_1[15:12] = c12_1 ? sumL1_1[15:12]: sumL1_0[15:12];
// Level three selecting the final outputs
assign c_out = c8 ? c16L2_1 : c16L2_0;
assign sum[15:8] = c8 ? {sumL2_1[15:12], sumL1_1[11:8]} : {sumL2_0[15:12], sumL1_0[11:8]};
endmodule原理图如下：
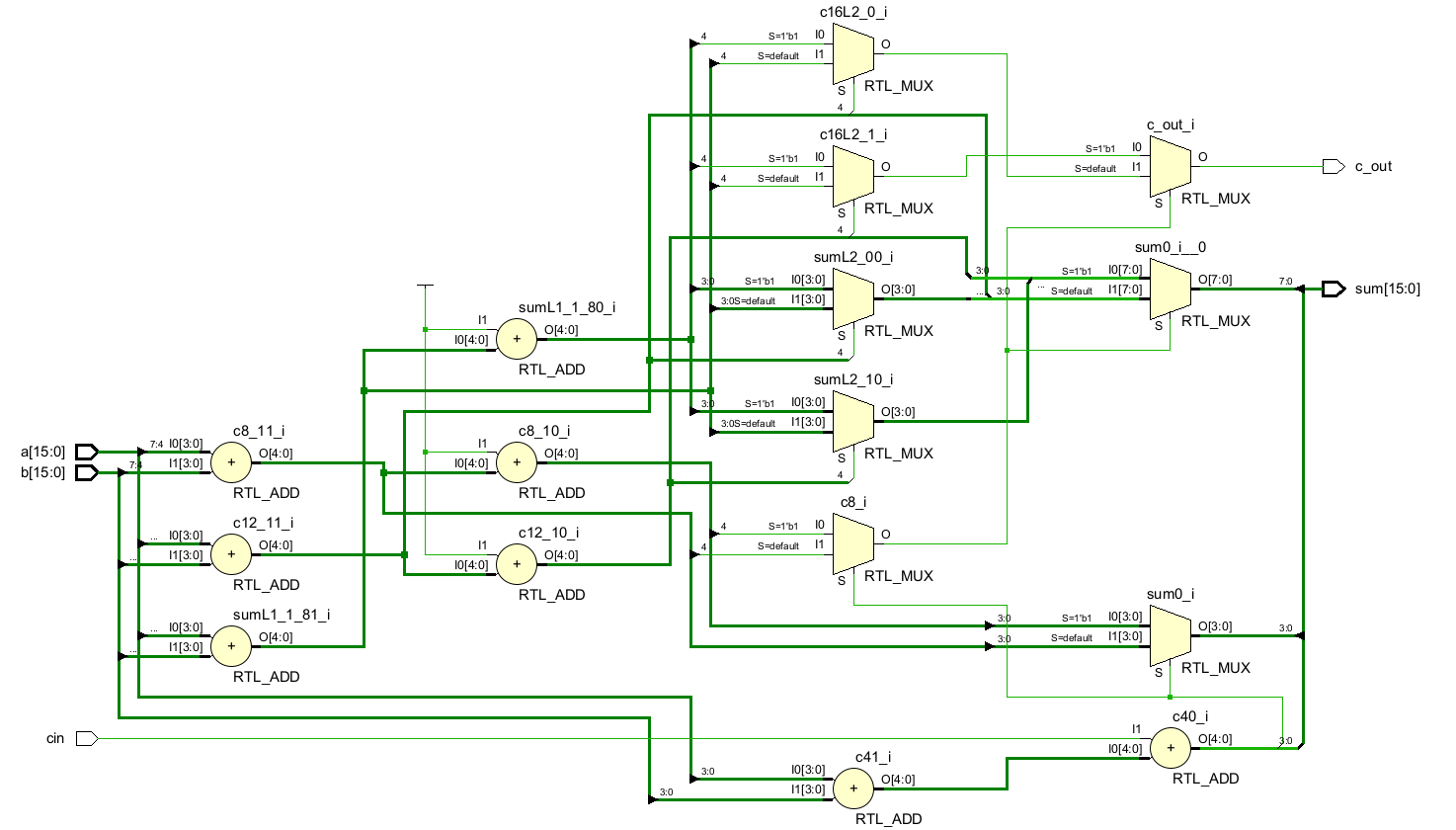
4. Carry Save Adder（进位保留加法器)
Carry Save Adder（CSA）它的内部结构实际上跟全加器FA一样，只是它不将进位传递给下一位，而是将其保留下来
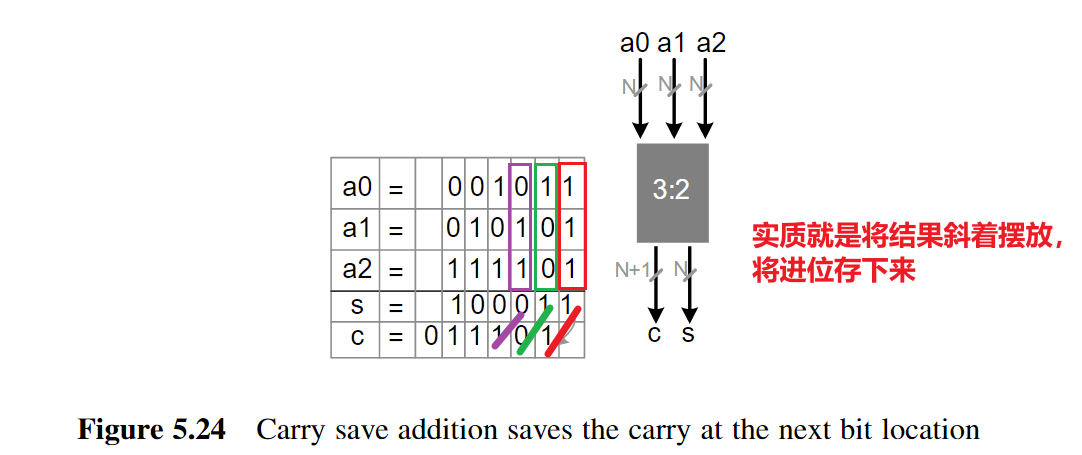
由此引申出来的CSA树，可以得到参考：数字IC前端学习笔记：数字乘法器的优化设计（进位保留乘法器）_日晨难再的博客-CSDN博客
乘法器
1.Wallace Tree乘法器
Wallace Tree是基于CSA的结构的，它能同时对不同的3bit结果使用CSA压缩成2bit，再在结果中又结合成3bit，继续压缩至2bit，直至最后压缩到只有2bit，此时可以用CLA去计算这个2bit的结果
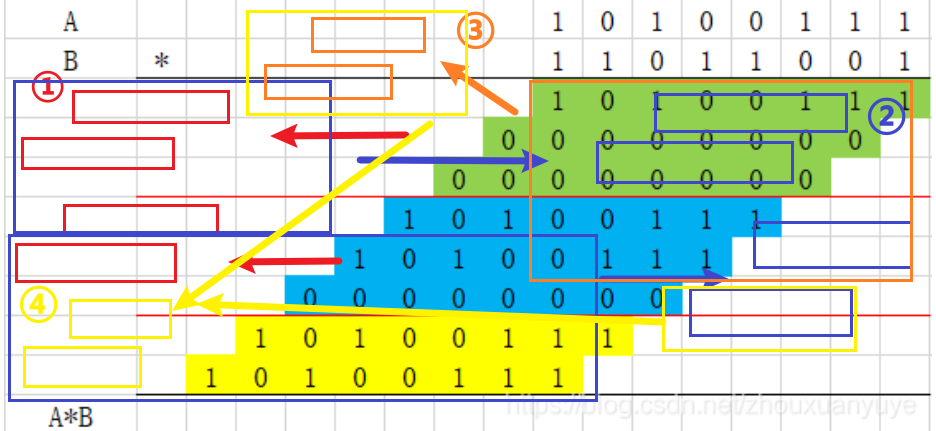
详情参考：【HDL系列】乘法器(4)——图解Wallace树_multiplier hdl-CSDN博客（写的非常形象）
例子参考：18a 數位邏輯設計 Fast Multiplier – Wallace Tree Example_哔哩哔哩_bilibili（视频中举例也十分清楚）
2.Booth乘法器
2.1 Radix2 Booth
Booth算法的目的是解决有符号乘法运算中复杂的符号修正问题，同时也能减少部分乘积项（PP）的数量
设n位乘法B的补码形式为：
$$
\begin{aligned}
B &= -B_{n-1}\cdot 2^{n-1}+B_{n-2}\cdot 2^{n-2}+\dots+B_1\cdot 2^1+B_0\cdot 2^0\
&= -B_{n-1}2^{n-1}+(\sum_{i=0}^{n-2}B_i\cdot2^i)
\end{aligned}
$$对上式做一些变换后可得到：
$$
B=\sum_{i=0,B_{-1}=0}^{n-1}(-B_i+B_{i-1})\cdot 2^i=\sum_{i=0}^{n-1}E_i\cdot 2^i
$$则有两个有符号乘积结果$P$：
$$
P=A\times B=A\times(\sum_{i=0}^{n-1}E_i\cdot 2^i) = \sum_{i=0}^{n-1}(A\times E_i)\cdot 2^i
$$- 其中：$E_i=-B_i+B_{i-1},0\le i \le n-1,B_{-1}=0$
- $E_i$称为编码值，$A\times E_i$称为部分积
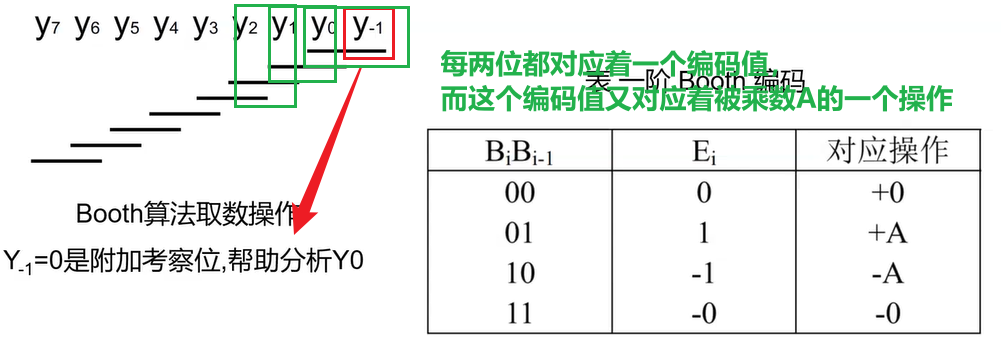
缺点：对于101010101010这样的乘数，需要计算的部分积个数没有变，反而多了编码的步骤，计算延迟增加，得不偿失，故实际中很少使用，而采用其优化而来的Radix4 Booth算法
2.2 Radix4 Booth
对于有符号数补码而言，扩展其最高位对数值并无影响。因此任何奇数位宽的有符号数补码都可以看成是偶数位宽
设一个二进制乘数B，位宽为n，且n为偶数，则B可以表示为：
$$
B=\sum_{i=0,B_{-1}=0}^{\frac n2-1}(-2B_{2i+1}+B_{2i}+B_{2i-1})\cdot 2^{2i}=\sum_{i=0}^{\frac n2 -1}E_i\cdot 4^i
$$则有两个有符号乘积结果$P$：
$$
P=A\times B=A\times \sum_{i=0}^{\frac n2 -1}E_i\cdot 4^i =\sum_{i=0}^{\frac n2 -1}(A\times E_i)\cdot 4^i
$$- 其中，$E_i=-2B_{2i+1}+B_{2i}+B_{2i-1},0\le i\le \frac n2 -1,B_{-1}=0$
- 且$\frac n2$为部分积的个数
Radix4 Booth算法每次编码的位数为3bit，使得部分积的数目减少为原始Booth算法的一半
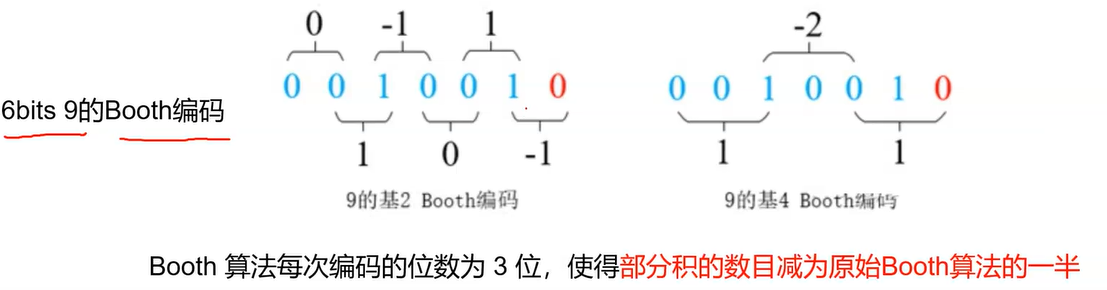
而Radix4 Booth的编码结果如下：
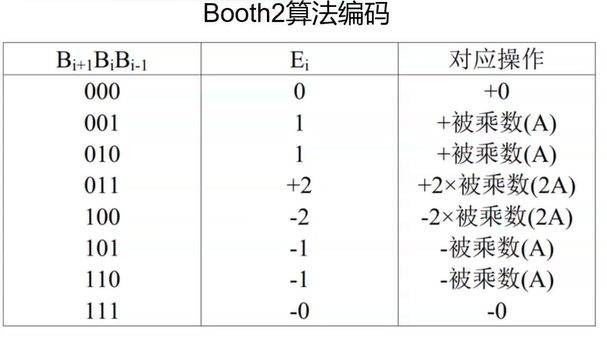
对除0外的操作都先对被乘数A的最高位添上一个符号位，再进行操作，+2A是左移，-2A代表取补码后左移（或者左移后再取补码也可）
Radix4 Booth编码实现的两个8bit有符号数相乘，输出为16bit有符号数
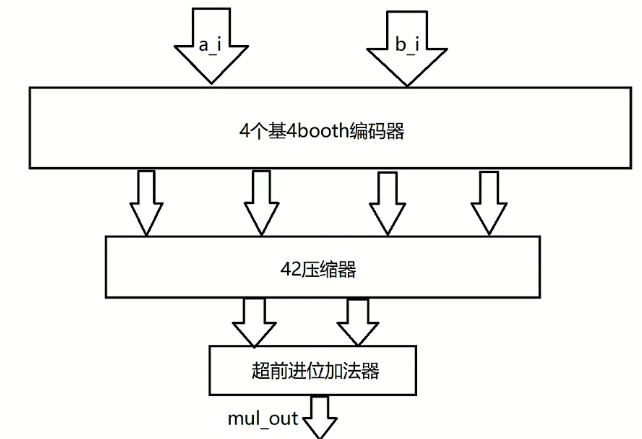
相关代码：
Booth_mul_top.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52module Booth_mul_top(
a_i,
b_i,
mul_o
);
parameter length = 8;
input [length-1 : 0] a_i,b_i;
output [length*2-1:0] mul_o;
wire [length : 0] booth_o0 ;
wire [length : 0] booth_o1 ;
wire [length : 0] booth_o2 ;
wire [length : 0] booth_o3 ;
wire [length*2-1: 0] pp0 ;
wire [length*2-1: 0] pp1 ;
wire [length*2-1: 0] pp2 ;
wire [length*2-1: 0] pp3 ;
//module booth4code (a_i,b_i,booth_o);
booth4code booth4_0 (a_i , {b_i[1:0],1'b0} , booth_o0 );
booth4code booth4_1 (a_i , b_i[3:1] , booth_o1 );
booth4code booth4_2 (a_i , b_i[5:3] , booth_o2 );
booth4code booth4_3 (a_i , b_i[7:5] , booth_o3 );
assign pp0 = {{ 7{booth_o0 [length]}} , {booth_o0 }}; //2*0
assign pp1 = {{ 5{booth_o1 [length]}} , {booth_o1 } , { 2{1'b0}}}; //<< 2
assign pp2 = {{ 3{booth_o2 [length]}} , {booth_o2 } , { 4{1'b0}}}; //<< 4
assign pp3 = {{ 1{booth_o3 [length]}} , {booth_o3 } , { 6{1'b0}}}; //<< 6
wire cout_0 ;
wire [length*2 : 0] cpr_o_0 ;
wire [length*2 : 0] cpr_o_1 ;
//wallace tree
//
//first level of wallace tree: 42compressor
//module compressor42 (in1,in2,in3,in4,cin,out1,out2,cout);
//out1 needs to be multiplied by two (out1<<1)
//module compressor42 (in1 ,in2 ,in3 ,in4 , cin ,out1 ,out2 ,cout );
compressor42 compressor42_1_0 (pp0 ,pp1 ,pp2 ,pp3 , 1'b0 ,cpr_o_0 ,cpr_o_1 ,cout_0 );
//本例中输入数据位宽是8，刚好一个42压缩即可，如果位宽较大，则需要进行多级位宽压缩
wire cout;
//carry lookahead adder
//module cla (op1,op2,sum,cout);
cla cla_0 (cpr_o_0[length*2-1:0]<<1 ,cpr_o_1[length*2-1:0] ,mul_o ,cout);
endmodulebooth4code.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27module booth4code(
a_i,
b_i,
booth_o
);
parameter length = 8;
input [length-1 : 0] a_i; //full 8-bit input
input [2:0] b_i; //3 of 8 bit input
output reg [length : 0] booth_o; //booth output
always @(*) begin
case(b_i)
3'b000 : booth_o <= 0;
3'b001 : booth_o <= { a_i[length-1], a_i};
3'b010 : booth_o <= { a_i[length-1], a_i};
3'b011 : booth_o <= a_i<<1;
//3'b100 : booth_o <= -(a_i<<1);
3'b100 : booth_o <= (-{ a_i[length-1], a_i})<<1;
3'b101 : booth_o <= -{a_i[length-1],a_i};
3'b110 : booth_o <= -{a_i[length-1],a_i};
3'b111 : booth_o <= 0;
default: booth_o <= 0;
endcase
end
endmodulecompressor42.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20module compressor42(
in1,in2,in3,in4,cin,out1,out2,cout
);
parameter length = 8;
input [length*2-1 : 0] in1,in2,in3,in4;
input cin;
output [length*2 : 0] out1,out2;
output cout;
wire [length*2-1 : 0] w1,w2,w3;
assign w1 = in1 ^ in2 ^ in3 ^ in4;
assign w2 = (in1 & in2) | (in3 & in4);
assign w3 = (in1 | in2) & (in3 | in4);
assign out2 = { w1[length*2-1] , w1} ^ {w3 , cin};
assign cout = w3[length*2-1];
assign out1 = ({ w1[length*2-1] , w1} & {w3 , cin}) | (( ~{w1[length*2-1] , w1}) & { w2[length*2-1] , w2});
endmodulecla.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23module cla(
op1,
op2,
sum,
cout
);
parameter width = 16 ;
input [width-1:0] op1;
input [width-1:0] op2;
output [width-1:0] sum;
output cout;
wire [width>>2:0] c; //16是4位宽，右移2位是2
assign c[0] = 1'b0;
assign cout = c[width>>2];
cla_4bit u_cla_4bit_0 (.op1( op1[ 0*4+3: 0*4] ),.op2( op2[ 0*4+3: 0*4] ),.cin( c[0 ] ),.sum( sum[ 0*4+3: 0*4] ),.cout( c[0 +1]));
cla_4bit u_cla_4bit_1 (.op1( op1[ 1*4+3: 1*4] ),.op2( op2[ 1*4+3: 1*4] ),.cin( c[1 ] ),.sum( sum[ 1*4+3: 1*4] ),.cout( c[1 +1]));
cla_4bit u_cla_4bit_2 (.op1( op1[ 2*4+3: 2*4] ),.op2( op2[ 2*4+3: 2*4] ),.cin( c[2 ] ),.sum( sum[ 2*4+3: 2*4] ),.cout( c[2 +1]));
cla_4bit u_cla_4bit_3 (.op1( op1[ 3*4+3: 3*4] ),.op2( op2[ 3*4+3: 3*4] ),.cin( c[3 ] ),.sum( sum[ 3*4+3: 3*4] ),.cout( c[3 +1]));
endmodulecla_4bit.v
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37module cla_4bit(
op1,op2,cin,sum,cout
);
parameter width = 4;
input [width-1:0] op1;
input [width-1:0] op2;
input cin;
output [width-1:0] sum;
output cout;
wire [width-1:0] g;
wire [width-1:0] p;
wire [width:0] c;
//gp generator
pg_gen u_pg_gen_0 (.a( op1[0]),.b( op2[0]),.g( g[0] ),.p( p[0] ));
pg_gen u_pg_gen_1 (.a( op1[1]),.b( op2[1]),.g( g[1] ),.p( p[1] ));
pg_gen u_pg_gen_2 (.a( op1[2]),.b( op2[2]),.g( g[2] ),.p( p[2] ));
pg_gen u_pg_gen_3 (.a( op1[3]),.b( op2[3]),.g( g[3] ),.p( p[3] ));
//carry generator
assign c[0] = cin;
assign c[1] = g[0] + ( c[0] & p[0] );
assign c[2] = g[1] + ( (g[0] + ( c[0] & p[0]) ) & p[1] );
assign c[3] = g[2] + ( (g[1] + ( (g[0] + (c[0] & p[0]) ) & p[1])) & p[2] );
assign c[4] = g[3] + ( (g[2] + ( (g[1] + ( (g[0] + (c[0] & p[0]) ) & p[1])) & p[2] )) & p[3]);
assign cout = c[width];
//sum generator
assign sum[0] = p[0] ^ c[0];
assign sum[1] = p[1] ^ c[1];
assign sum[2] = p[2] ^ c[2];
assign sum[3] = p[3] ^ c[3];
endmodulepg_gen.v
1
2
3
4
5
6
7
8
9
10
11
12
13module pg_gen(
a,b,g,p
);
input a;
input b;
output g;
output p;
assign g = a & b;
assign p = a ^ b;
endmoduleTestbench
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63module Booth_mul_tb;
reg [7 : 0] a_i,b_i;
wire [15 : 0] mul_o;
Booth_mul_top u0(
.a_i(a_i),
.b_i(b_i),
.mul_o(mul_o)
);
integer i;
initial begin
a_i = 8'b1111_1111;
b_i = 8'b1111_1111;
#10;
a_i = 8'b1000_1111;
b_i = 8'b0000_0010;
#10;
a_i = 8'b0000_0010;
b_i = 8'b0000_0001;
#10;
a_i = 8'b1000_0010;
b_i = 8'b0000_0001;
#10;
a_i = 8'b1000_0010;
b_i = 8'b1000_0001;
#10;
b_i[3:1] = 3'b001;
a_i = 8'b1111_1111;
b_i = 8'b1111_1111;
#10;
a_i = 8'b1111_1111;
b_i = 8'b0000_0010;
#10;
a_i = 8'b1111_1111;
b_i = 8'b1111_1111;
#10;
a_i = 8'b1111_1111;
b_i = 8'b0000_0000;
for (i = 0; i<10; i=i+1) begin
a_i = a_i + 1;
b_i = b_i + 1;
#10;
end
end
initial begin
#1000 $stop;
end
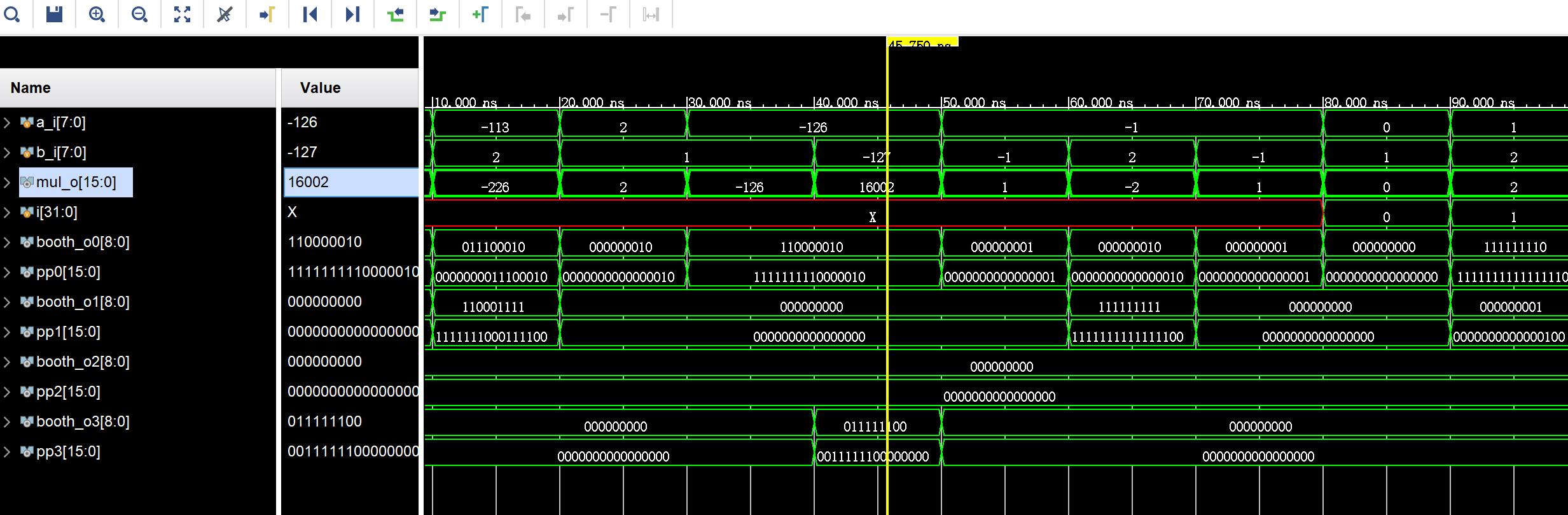
endmodule仿真结果如下：
