本节主要介绍了利用FFT进行频谱分析以及滤波器结构
应用FFT分析信号频谱
1.谱线与实际频率的关系
DTFT的幅频特性是以$w$数字角频率$2\pi$为周期的函数
而DFT的幅频特性的横坐标是$0\sim N-1$,故其共有$N$个点
数字角频率和模拟角频率的关系为$w\times f_s=\Omega$
故$w=2\pi$就对应模拟频率$f_s$,就对应第$N$个点,即第$N$个点所对应的实际频率就是$f_s$
- 这么分析看似没问题吧,但是,有个问题是DFT的横坐标$k$,只能取$0\sim N-1$,$k=0$的点占了一个零频,故即使点与点之间的频率间隔是$\frac{f_s}{N}$,那么最终能取到的最大频率只能是$\frac{(N-1)}{N}\cdot f_s$
故谱线与实际频率的对应关系为:
- 其中,$N_i$代表第$i$个点,而第$N_i$个点有$N_i-1$个频率间隔
借助MATLAB程序加深理解
1
2
3
4
5
6
7
8
9
10
11
12
13clc;clear all;
fs=1000;
N=500;
xn=0:(N-1);
t=xn/fs; %这里的t代表信号长度,而1/t也决定了实际分辨率
f0=0;
f1=2;
f2=680;
s=cos(2*pi*f0*t)+cos(2*pi*f1*t)+cos(2*pi*f2*t);
s_fft=abs(fft(s,N));
stem(xn,s_fft);结果如下:
- 根据上述公式,通过计算得到$f_0,f_1,f_2$对应第1,2,161个点,那么对应的$k$值为0,1,160(这里用1000-680KHz的频率去计算)
- 从上述结果也能很明显的看出$x(k_0)=x(N-k_0)$(这个结论对$f_0=0$不适用)
- 同时,也可以得出$k=0$这一点确实对应着零频
2.栅栏效应与实际分辨率
栅栏效应:就是真实频率落在了点与点之间的缝隙里,补零操作可以缓解栅栏效应
实际分辨率:
借助MATLAB程序加深理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26clc;clear all;
fs=100;
N=100;
xn=0:(N-1);
t=xn/fs; %这里的t代表信号长度,而1/t也决定了实际分辨率
f0=10;f1=11;
s=sin(2*pi*f0*t)+sin(2*pi*f1*t);
xn=xn/N*fs;%此时xn横坐标为实际频率
s_fft=abs(fft(s,N));
s_zero_fft=abs(fft(s,2*N));
figure(1);
subplot(211);
plot(xn,s_fft);
title("N=500 FFT")
xlabel('f/Hz')
ylabel('Amp')
grid on;
subplot(212);
plot([0:199]/200*fs,s_zero_fft);
title("N=500 padding=500 FFT");
xlabel('f/Hz')
ylabel('Amp')
grid on;结果如下:
- 虽然说理论上1Hz可以分辨开,但由于实际观察时显示分辨率不够,所以导致通过观察频谱图无法分辨出两个目标
不补零的情况下,能够分辨的频率间隔其实是$2\times d_f$
时域离散系统的网络结构
网络的基本组成结构:
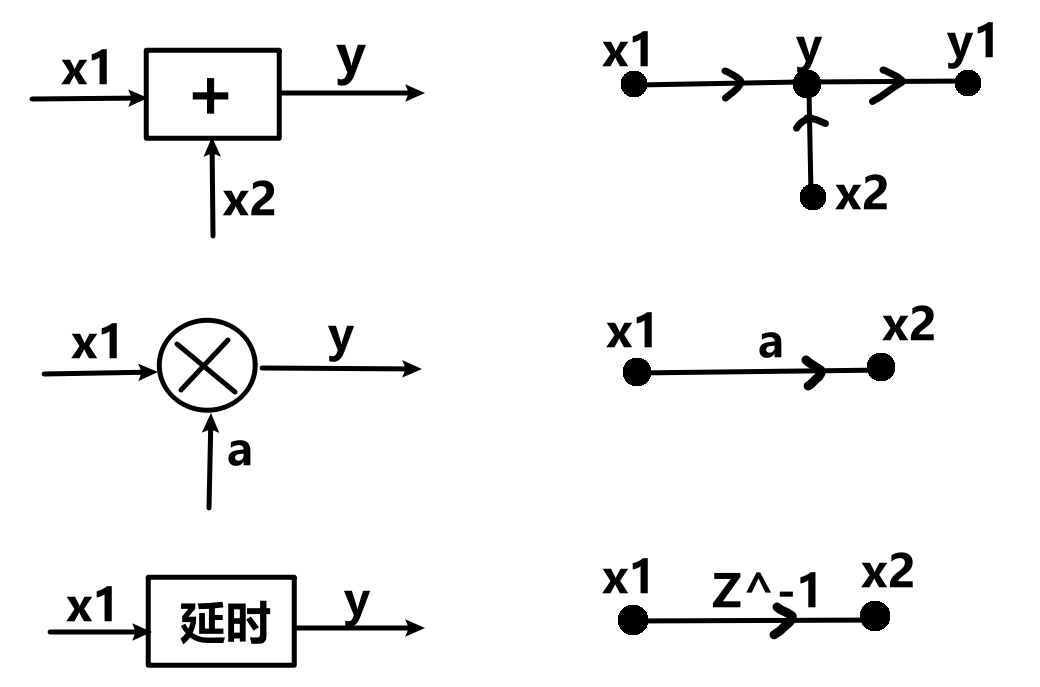
1.IIR的网络结构
IIR的差分方程:
直接Ⅰ型结构:
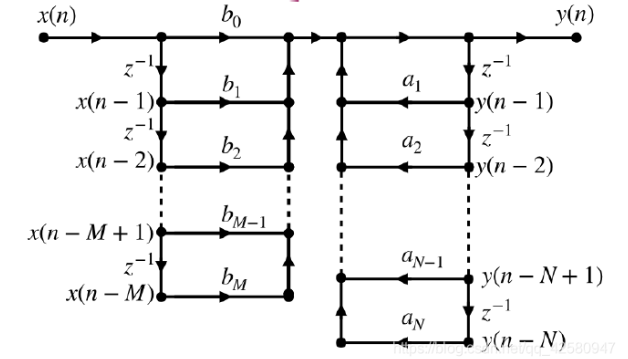
直接Ⅱ型结构:
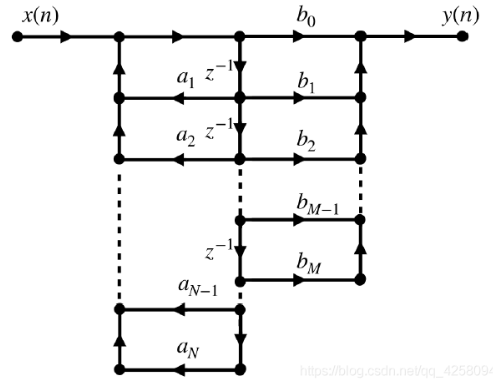
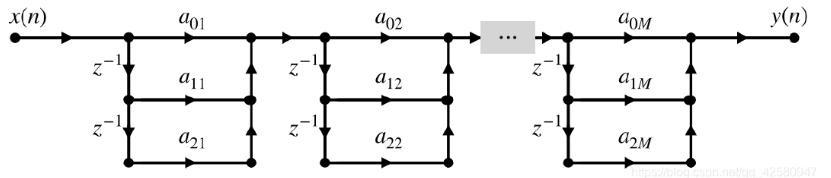
级联型结构:
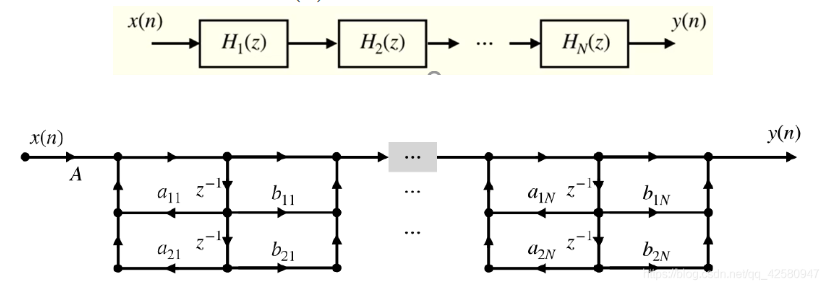
2.FIR的网络结构
- FIR的差分方程:
直接型结构:
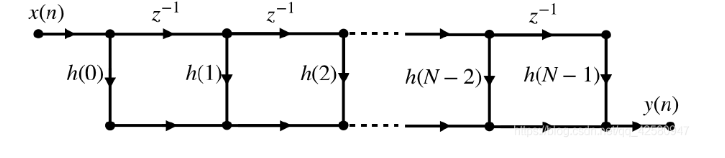
级联型结构: