本节主要介绍了雷达信号的数学表示、模糊函数与雷达分辨率的关系、线性调频脉冲信号及其压缩处理、多脉冲积累的处理方法
雷达信号的数学表示
雷达的发射信号一般是除初相外其余参量均已知的确知信号
回波信号则是与噪声、干扰叠加的随机信号
信号可以用时间的实函数$s(t)$表示,称为实信号,其特点具有有限的能量或有限的功率
能量有限的信号称为能量信号,描述能量信号的频谱特性通常采用能量谱密度(ESD)函数
- 其中$s(t)$代表信号
能量无限但功率有限的信号,称为功率信号,对于功率信号,功率谱密度(PSD)函数定义为:
- 其中$r_s(t) = \int_{-\infty}^{\infty}s^*(\tau)s(t+\tau)d\tau$为信号$s(t)$的自相关函数
按照信号的频率组成,可将信号划分为低通信号(Low Pass)信号和带通(Band Pass)信号。通常所用的雷达信号,其带宽比载波小很多,称为窄带(通)信号
一个实带通信号可表示为:
- 其中:$a(t)$为信号的幅度调制或包络,$\phi_x(t)$为相位调制项,$f_0$为载频
- 对于低分辨雷达,在一个波位上发射的多个脉冲的目标回波的包络$a(t)$通常近似认为不变
信号$x(t)$的频率调制函数$f_m(t)$和瞬时频率$f_i(t)$分别为:
实信号具有对称的双边频谱
- 对于窄带信号来说,由于其带宽远小于载频,两个边带频谱互不重叠,此时用一个边带频谱就能完全确定信号波形。为了简化信号和系统的而分析,通常采用具有单边频谱的复信号
- 常用的复信号白哦是,即实信号的复信号表示有两种:希尔伯特(Hilbert)变换法和指数表示法,对于窄带信号来说,这两种表示方法是近似相同的
1. 希尔伯特(Hilbert)变换表示法
一般地,复信号可表示为:
- 如果要求复信号具有单边频谱,那么就要对虚部有所限制
如果实信号$x(t)\Leftrightarrow X(f)$($X(f)$为信号$x(t)$的傅里叶变换),定义其复解析信号为:
其中$U(f)$为频域的阶跃函数,利用傅里叶变换的性质可得:
- 其中,$\hat x(t) = \frac 1\pi \int_{-\infty}^{\infty}\frac{x(\tau)}{t-\tau}d\tau$为$x(t)$的Hilbert变换式
- 这样,复信号的频谱就可以满足使得原始实信号的负频分量相抵消,而正频分量加倍
实信号$x(t)$的能量和复解析信号$s_a(t)$的能量分别为:
2. 指数表示法
复解析信号在推导信号的一般特性时是有效的表示方式,但在分析具体信号时又极不方便,故常采用指数形式的复信号来代替复解析信号
实信号用指数形式的复信号实部表示为:
- 其中,$s_e(t) = a(t)e^{j[2\pi f_0 t+\phi_xt]} = u(t)e^{j2\pi f_0 t}$为实信号的复指数形式,而$u(t) = a(t)e^{j\phi_x(t)}$为复信号的复包络
窄带实信号、复信号和复包络之间的关系:
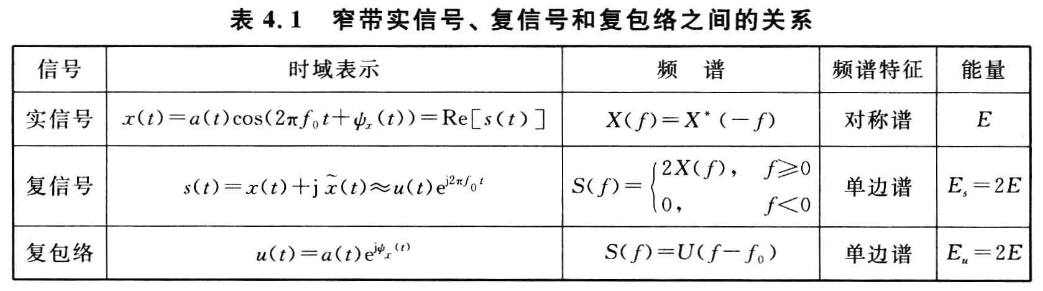
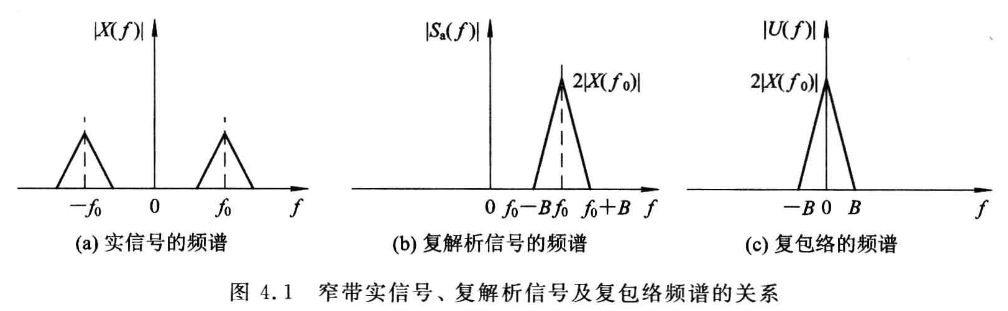
模糊函数与雷达分辨率
1. 模糊函数
模糊函数最初是为了研究雷达分辨率而提出的,两个目标距离和速度上的差异是刚好可以用来相关函数模拟的,越相似相关函数越大,说明两个目标越难以区分
利用一对二维变量$(\tau, f_d)$来描述模糊函数,假设目标1和目标2的时延分别为$d$和$d+\tau$,多普勒频移分别为$f$和$f+f_d$,且功率相同
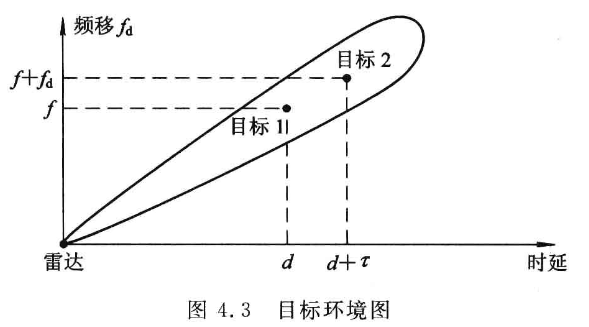
雷达的发射信号通常为窄带信号,用复信号可表示为:
目标1的回波信号可表示为:
则目标2的回波信号可表示为:
在分析分辨力时,通常利用积分方差来描述,具体来说就是当积分方差越大时,两个目标就越好区分
- 设$y_1 = X_R + jX_I, y_2 = X_R’+jX_I’$
- $|y_1-y_2|^2 = X_R^2+X_R’^2-2X_RX_R’+X_I^2+X_I’^2-2X_IX_I’^2$
- 其中:$X_R^2+X_I^2 = |y_1|^2, X_R’^2+X_I’^2=|y_2|^2$
- $y_1y_2* = X_RX_R’-jX_RX_I’+jX_IX_R’+X_IX_I’$
- 故:$|y_1-y_2|^2 = |y_1|^2+|y_2|^2-2Re|y_1y_2^*|$
故积分方差为:
定义$\chi(\tau,f_d)$为:
则模糊函数为:
- $|\chi(\tau,f_d)|$式决定相邻目标距离-速度联合分辨率的唯一因素
- 有的文献也把$|\chi(\tau,f_d)|^2$当作模糊函数
由上述分析可得:
故$|\chi(\tau, f_d)|$的最大值为$2E$,此时两个目标重叠在一起,距离和速度一样
那么就意味着$\tau = 0,f_d =0$,即:
能够引起$\varepsilon^2 $被滤波器检出,那么这两个目标也就可以分开了。如果保持不$f_d$变,最小的$\tau$值引起的$\varepsilon^2 $能被滤波器检出,此时$\tau$对应的就是距离分辨率。同理多普勒分辨率
2. 分辨率
2.1 距离分辨率
假设两个目标在同一角度但处在不同距离上,在不考虑相邻目标的多普勒频移($f_d = 0$)时,有:
此时,信号的距离模糊函数为:
当$\tau = 0$时,$|\chi(\tau,0)|$有最大值,距离分辨率由$|\chi(\tau,0)|^2$的大小来衡量
当$\tau\neq 0$时,$|\chi(\tau,0)|$随$\tau$增大而下降的越快,距离分辨性能越好
时延分辨率为:
根据Parseval定理,上式可重写为:
$B$为信号的有效带宽
因此,时延分辨率对应的距离分辨率为:
只要信号具有大的持续带宽就能获得高的距离分辨率,而不必具有很窄的脉冲宽度
2.2 速度分辨率
与距离分辨率类似,信号的速度分辨率取决于速度模糊函数:
则多普勒分辨率$\Delta f_d$为:
- 式中:$\tau’$是脉冲宽度
则相应的速度分辨率$\Delta v$为:
2.3 距离-速度联合分辨率
定义模糊面积$AA$作为距离-速度联合分辨常数:
- 只要信号能量一定,模糊面积即为定值1
- 这就说明了时延和多普勒联合分辨率的限制,无论怎么使时延$\tau$或多普勒$f_d$分辨率的某一方减小,其结果都将带来另一方的增大,这就是雷达模糊原理
- 设计雷达信号时,只能在模糊原理的约束下通过改变模糊曲面的形状,使之与特定的目标环境相匹配
线性调频(LFM or Chirp)脉冲信号
- 线性调频信号是一种脉冲压缩信号,它是在匹配滤波理论的基础上提出的
这种信号的突出优点是匹配滤波器对回波信号的多普勒频率不敏感,即使回波信号有较大的多普勒频移,匹配滤波器仍能起到脉冲压缩的作用
线性调频矩形脉冲信号的表达式写为:
其中,信号的复包络为:
- $T$为脉冲宽度,$\mu=\frac BT$为调频斜率,$B$为调频带宽,也称频偏
信号的瞬时频率为:
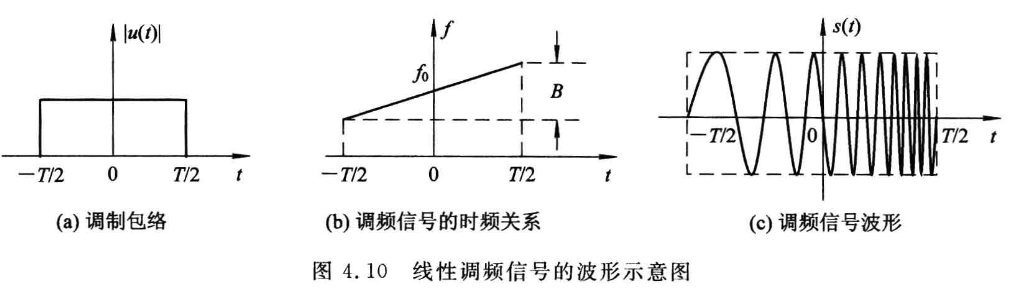
线性调频信号的频谱由信号的复包络完全决定
当$BT\gg1$时,信号95%以上的能量集中在$-\frac B2\sim \frac B2$的范围,频谱接近于矩形
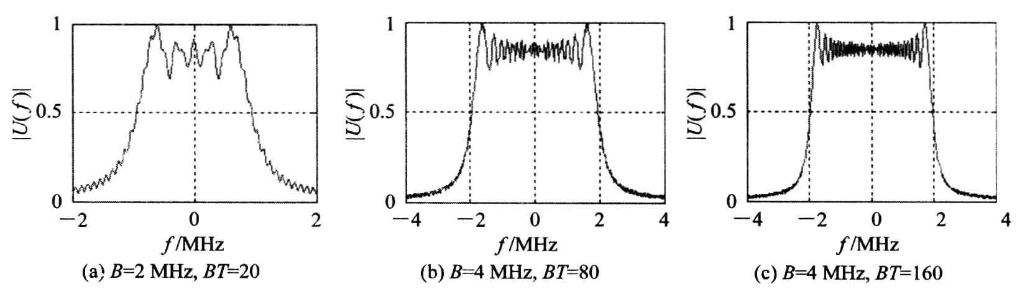
线性调频脉冲信号的压缩处理
雷达系统为了满足提高探测距离和距离分辨率的双重要求,就要求采用大时宽 带宽 积 信号。脉冲压缩处理将发射的宽脉冲信号压缩成窄脉冲信号,它既可以发射宽脉冲以提高平均功率和雷达的检测能力,又能保持窄脉冲的距离分辨率
假设雷达发射线性调频脉冲信号,可表示为:
式中,$rect(\frac{t}{T_e})=1,|t|\le \frac12 T_e$,$T_e$为发射脉冲宽度,$f_0$为中心载频,$\mu = \frac B{T_e}$为调频斜率,$B$为调频带宽
该信号的复包络及其离散信号(采样间隔为$T_s$)为:
假设目标初始距离$R_0$对应的时延为$t_0$,即$t_0 = \frac{2R_0}{c}$,目标的径向速度为$v$,若不考虑幅度的衰减,则接收信号及其相对于发射信号的时延分别为:
则有:
其中:
这一部分暂时还没完全整明白,等整明白了再来记录
- 匹配滤波器的压缩比??
- 为什么脉冲压缩对多普勒频率不敏感?
在频域和时域上的匹配滤波到底有个啥区别?
多脉冲积累的处理方法
1.多脉冲积累的概念
因为雷达单个脉冲的回波能量是有限的,通常不采用单个接收脉冲来进行检测判决
在判决之前,先对一个波位的多个脉冲串进行处理,以提高信噪比
这种基于多个脉冲串而非单个脉冲的处理方法称为积累
从时域上来说,积累是将一个波位内连续的M个重复周期同一距离单元的回波信号叠加起来(或加权叠加)

- 上述数据矩阵的横坐标为距离单元,由快时间采样得到;纵坐标为每个脉冲重复周期,在雷达中经常称其为慢时间采样
积累分相干积累和非相干积累:
- 相干积累是在包络检波器之前进行,利用接收脉冲之间的相位关系,可以获得信号幅度的叠加。这种积累起可以把所有的雷达回波能量直接相加
- 非相干积累是在包络检波以后进行,也称之为检波后积累或视频积累。由于信号在包络检波后失去了相位信息而只保留下幅度信息,所以检波后积累就不需要信号间有严格的相位关系,因此称为非相干积累
2.相干积累的处理方法
由于运动目标的回波包括多普勒频率$f_d$,当脉冲雷达的每个脉冲重复周期$T_r$相等,如果忽略目标回波的幅度起伏,则对目标所在距离单元的信号在每个$T_r$采样时,就可以看作是对频率为$f_d$的正弦波的采样,这时,第$i$个脉冲重复周期对目标的采样值可以表示为:
- 式中$M$表示在一个波位(半功率波束宽度)内发射的脉冲数
- 若$M$不是2的幂,则通过补零到2的幂(即$N = 2^n \ge M$),因为相干累加通常采用$FFT$的处理方法实现
- 上图中包括$L$个距离单元,则需要进行$L$次$2^n$点的$FFT$处理
于是目标所在距离单元、所在多普勒通道的输出为:
- 上式只有当$f_d=\frac{k}{T_rN}=\frac{k}{N}f_r$时才出现峰值
相干积累的特点:
- $M$个脉冲进行相干积累的信噪比改善可以达到单个脉冲的$M$倍
- 也就是说,若要达到同样的检测性能,对单个脉冲的检测因子可以减低为$\frac1M$
- 因此,相干脉冲有利于降低发射功率或提高检测性能
