本节主要介绍了矩阵的特征值与特征向量、相似矩阵、矩阵可对角化的条件以及实对称矩阵的对角化
矩阵的特征值与特征向量
1.基本概念
- A是n阶方阵,对于一个数$\lambda$,存在非零列向量,使得$A\alpha=\lambda\alpha$成立,那么$\lambda$为特征值,$\alpha$为对应$\lambda$的特征向量
- $\lambda$可以为0,但特征向量不能为0向量
- 特征方程:$|\lambda E-A|=0$
- 通过求解特征方程计算$\lambda$,求出$\lambda$后带入$(\lambda E-A)\alpha=0$中求解齐次方程,而方程的基础解系就是特征向量
- 若能证明两个矩阵的$|\lambda E-A|$相等,那么就说明这两个矩阵有相同的特征值
- $\lambda$是A的特征值,$\alpha$是$\lambda$对应的特征向量,则$c\alpha$也是$\lambda$的特征向量$(c\ne 0)$
- 一个特征向量只能对应一个特征值
若$\alpha_1,\alpha_2$是$\lambda$的特征向量,则$c_1\alpha_1+c_2\alpha_2$也是$\lambda$的特征向量
上三角矩阵中,n阶对角线上的特征值就是主对角线上的n个元素
2.基本性质
- $A$和$A^T$有相同的特征值,但其特征向量不一定相同
- 若矩阵A有n个特征值$\lambda_1,\lambda_2,…,\lambda_n$,有:
- $\sum_{i=1}^{n}\lambda_i=\sum_{i=1}^na_{ii}$:特征值相加等于主对角线元素相加
- $\lambda_1\lambda_2…\lambda_n=|A|$:特征值相乘等于矩阵的行列式
- 互不相同的特征值$\lambda_1,\lambda_2,…,\lambda_m$对应的特征向量$\alpha_1,\alpha_2,…,\alpha_m$线性无关
- k重特征根对应的特征向量个数$\le k$(单根对应的特征向量就为1)
- $k\lambda$是$kA$的特征值
- $\lambda^k$是$A^k$的特征值
- 若$\lambda$是$A$的特征值,则:
- $\frac{1}{\lambda}是$$A^{-1}$的特征值
- $\frac1{\lambda}|A|$是$A^*$的特征值
相似矩阵和矩阵可对角化的条件
1.相似矩阵
相似矩阵:若A、B为n阶方阵,若存在n阶可逆矩阵P,使得$P^{-1}AP=B$成立,则说明$A\sim B$(A相似于B)
- $A\sim A$
- 若$A\sim B$,则$B \sim A$
- 若$A\sim B,B\sim C$,则$A\sim C$
相关性质:
- 若$A\sim B$,则$A、B$具有相同的特征值,且$|A|=|B|$,特征值之和相等
- 若$A\sim B$,则$A可逆\Leftrightarrow B可逆$,$A^{-1}\sim B^{-1}$
- 若$A\sim B$,则$A^m\sim B^m$
2.矩阵可角化条件
A相似于对角形矩阵(只在对角线有元素,其他位置为0)$\Leftrightarrow$A有n个线性无关的特征向量
若A有n个不相同的特征根,则A相似于对角形
对角形矩阵为:
可逆矩阵P为:
A相似于对角形矩阵$\Leftrightarrow r_i$重根的基础解系有$r_i$个
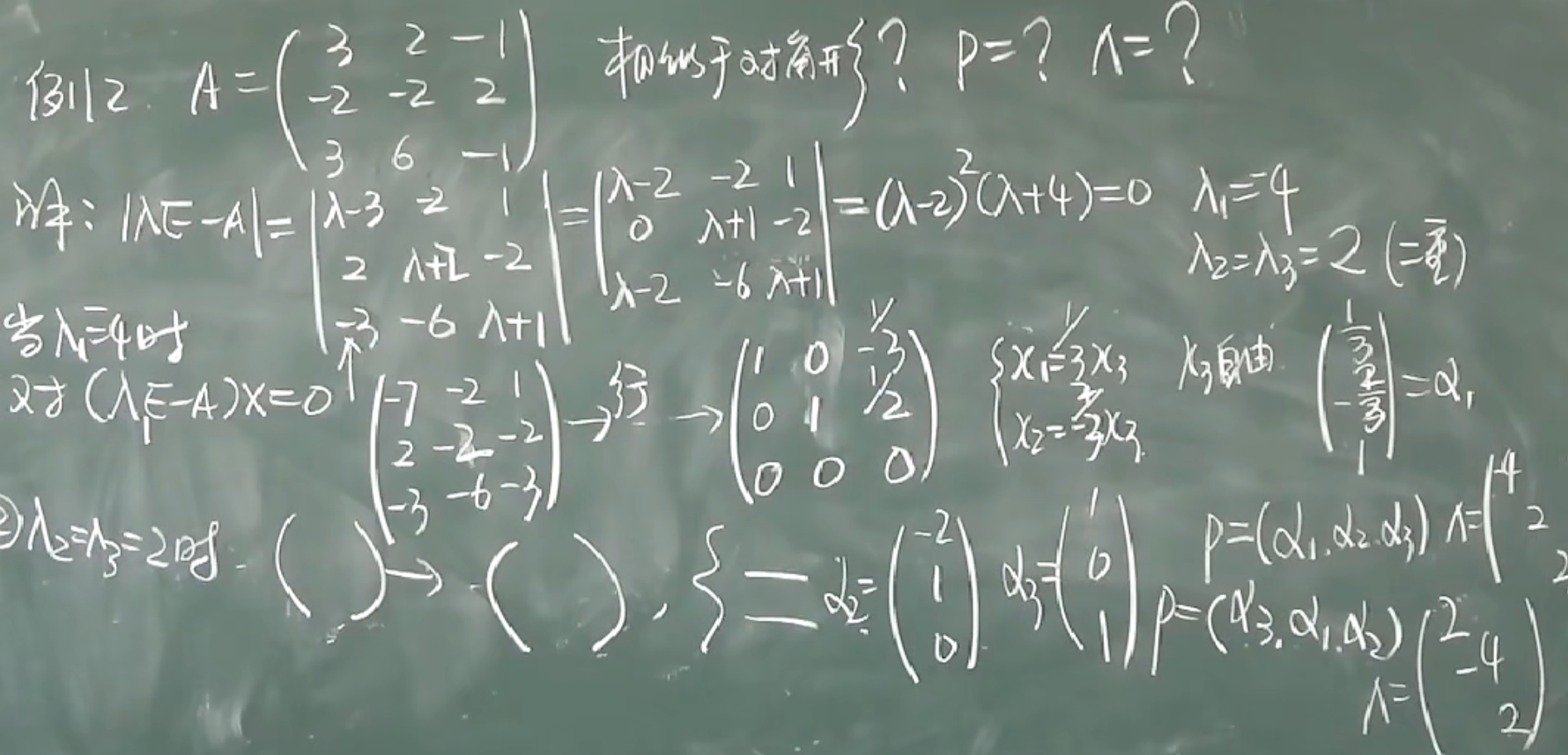
实对称矩阵的对角化
1.向量的长度(范数、模)
计算公式:
其中(,)表示进行内积运算
单位化(标准化):使得模值为1
相关性质
- $||\alpha||\ge 0$
- $||\alpha||=0\Leftrightarrow \alpha=0$
- $||k\alpha||=|k|\cdot||\alpha||$
柯西-施瓦茨不等式:
三角形不等式:
2.正交(垂直)
定义:$(\alpha,\beta)=0$
正交向量组:不含零向量的一组$a_1,a_2,…,a_s$向量两两正交
标准正交向量组:
定理:$a_1,a_2,…,a_s$是正交向量组,则$a_1,a_2,…,a_s$是线性无关的
3.正交矩阵
- 定义:A为n阶方阵,若满足$A^T A=E$,则A为正交矩阵
- 相关性质:
- 若A为正交矩阵,那么$|A|=1\,or\,-1$
- 若A为正交矩阵,那么$A^{-1}=A^T$,且$A^{-1}$和$A^T$均为正交矩阵
- 若A、B为正交矩阵,那么AB也为正交矩阵
- 若A为正交矩阵,$\alpha,\beta$为列向量,则$(A\alpha,A\beta)=(\alpha,\beta)$
- 相关定理:A为正交矩阵$\Leftrightarrow$A的列(行)向量组是标准正交向量组
4.正交相似
- A、B是同阶方阵,若存在正交矩阵P,使得$P^{-1}AP=B$成立,则称A正交相似于B
5.实对称矩阵
- 实对称矩阵的定义:$A^T=A$
- 定理:实对称A的不同特征值的特征向量正交
- 实对称矩阵一定能对角化
