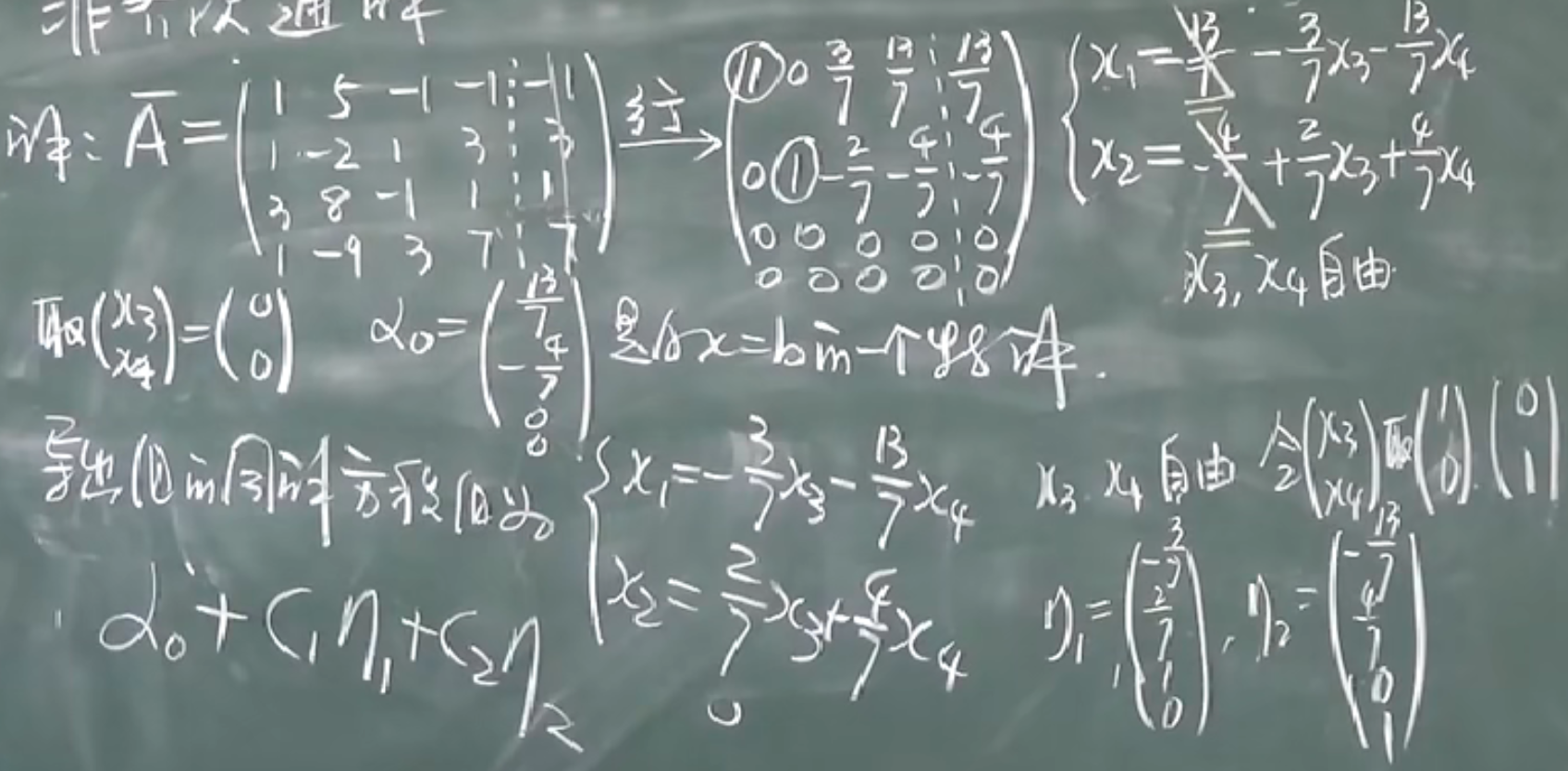本节主要介绍了非齐次线性方程与齐次线性方程的解法

线性方程组有解判定

若由如下方程组：
$$
\begin{cases}
\begin{aligned}
x_1 + x_2 + x_3 &= 1\
x_1 - x_2 - x_3 &= -3\
2x_1 + 9x_2 + 10x_3 &= 11\
\end{aligned}
\end{cases}
$$
则系数矩阵为：
$$
A=\begin{bmatrix}
1 & 1 & -1\
1 & -1 & -1\
2 & 9 & 10\
\end{bmatrix}
$$
增广矩阵为：
$$
\bar A=\begin{bmatrix}
1 & 1 & -1 & 1\
1 & -1 & -1 & -3\
2 & 9 & 10 & 11\
\end{bmatrix}
$$
在方程组中，通常用m表示方程个数，n表示未知量的个数
是否有解的判断方式：
- 当$r(A)=r(\bar A)$时，方程组有解：
  - 若$r(A)=r(\bar A)=n$，则方程组有唯一解
  - 若$r(A)=r(\bar A)<n$，则方程组有无穷多解
- 当$r(A)\ne r(\bar A)$时，方程组无解

齐次线性方程组

方程组$Ax=b$中，向量$b$为0向量，即$Ax=0$则称为齐次线性方程组
齐次线性方程组一定有解，至少有零解
齐次线性方程组解的情况：
- 有唯一零解$\Leftrightarrow r(A)=n$
- 有非零解$\Leftrightarrow r(A)<n$
- 方程个数m<未知数个数n$\Leftrightarrow$有非零解
- 方程个数=未知数个数，有非零解$\Leftrightarrow |A|=0$
齐次方程中$Ax=0$，那么：
- 若$\eta_1$和$\eta_2$是齐次方程组的解，那么$\eta_1+\eta_2$也是方程组的解
- 若$\eta$是$Ax=0$的解，那么$c\eta$也是方程组的解

齐次方程的基础解系：$\eta_1,\eta_2,…,\eta_s$需满足如下条件
- $\eta_1,\eta_2,…,\eta_s$线性无关
- 任何解都可以由$\eta_1,\eta_2,…,\eta_s$表示
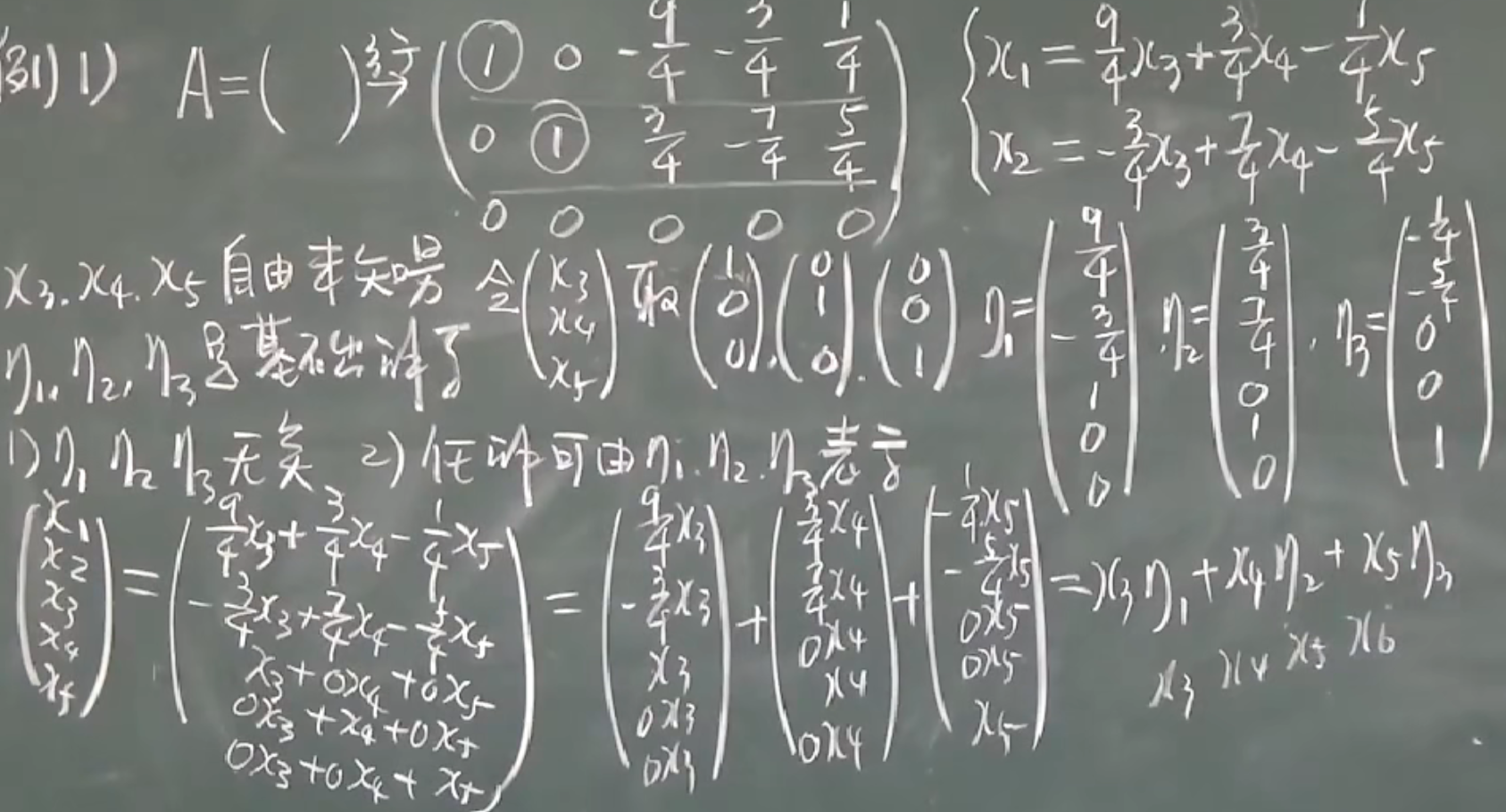
基础解系的个数$=n-r(A)$
若$A_{m\times n}B_{n\times s}=0_{m\times s}$，则$r(A)+r(B)\le n$

对于非齐次线性方程组$Ax=b$：
- 若$\alpha_1,\alpha_2$是$Ax=b$的解，$\alpha_1-\alpha_2$是$Ax=0$的解
- 若$\alpha_0$是$Ax=b$的解，$\eta$是$Ax=0$的解，那么$\alpha_0+\eta$也是$Ax=b$的解
非齐次线性方程解的结构=（$Ax=b$的一个特解）+（$Ax=0$的基础解系的线性组合）