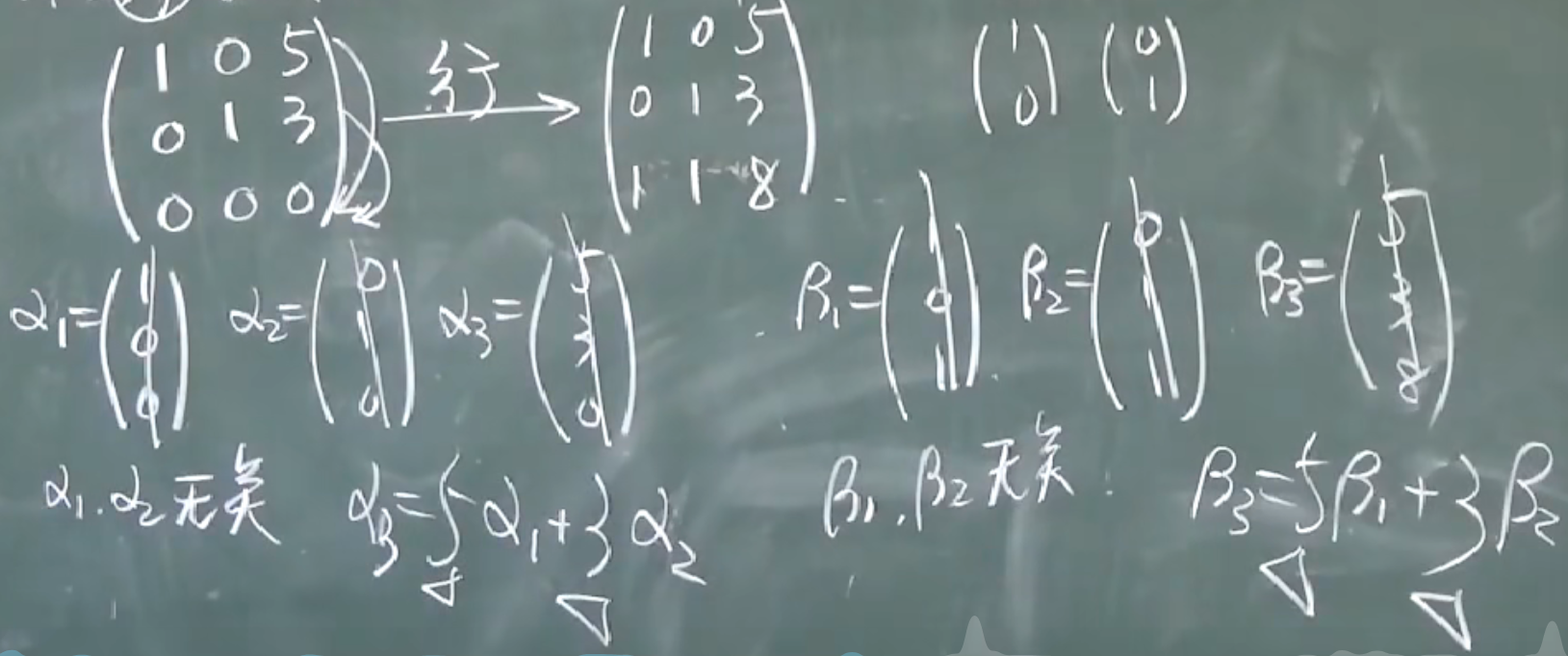本节主要介绍了向量的基本概念、线性相关与线性无关、向量组的秩
n维向量以及运算
向量：n个数$a_1,a_2,…,a_n$组成的有序数组（向量组），其中$a_1,a_2,…,a_n$称为分量，记作$\alpha、\beta、\gamma$
定理：$k\alpha=0\Leftrightarrow k=0,or,\alpha=0$
线性组合：$\beta,\alpha_1,\alpha_2,…,\alpha_n$是m维向量，若存在$k_1,k_2,…,k_n$使得下式成立：
$$
\beta=k_1\alpha_1+k_2\alpha_2+…+k_n\alpha_n
$$
则称$\beta$是$\alpha$向量们的线性组合，$k_1,k_2,…,k_n$为组合系数，系数可全取0零向量可由任意向量组表示
向量组中任意向量可由向量组表示
任意向量都可由：$\epsilon_1=(1,0,…,0)、\epsilon_2=(0,1,…,0)、…、\epsilon_n=(0,0,…,1)$表示
线性相关与线性无关
线性相关：$a_1,a_2,…,a_n$是n个m维向量，若存在一组不全为0的$k_1,k_2,…,k_n$系数，使得：
$$
k_1\alpha_1+k_2\alpha_2+…+k_n\alpha_n=0
$$
则$a_1,a_2,…,a_n$是线性相关线性无关：使得$k_1\alpha_1+k_2\alpha_2+…+k_n\alpha_n=0$的$k_1,k_2,…,k_n$系数只有全为0的情况
相关结论：
- 向量组中两向量成比例，则线性相关
- 含零向量的向量组必线性相关
- 只有一个零向量必线性相关
- 任意一个非零向量必线性无关
- 若一个向量$\alpha$线性相关，则$\Leftrightarrow\alpha=0$
- 若$a_1,a_2,…,a_r$线性相关，则$a_1,a_2,…,a_r,a_{r+1},…,\alpha_s$也线性相关
- 整体向量组线性无关，则部分向量组也线性无关
- 线性无关的向量组，其接长向量组也线性无关
- 线性相关的向量组，其截短向量组也线性相关
- 向量的个数等于向量的维数时，n个n维向量的$D\ne0\Leftrightarrow$线性无关，$D=0\Leftrightarrow$线性相关
- $\epsilon_1=(1,0,…,0)、\epsilon_2=(0,1,…,0)、…、\epsilon_n=(0,0,…,1)$线性无关
相关定理：
- 若$a_1,a_2,…,a_s$线性相关$\Leftrightarrow$至少一个向量可由其余向量表示
- 若$a_1,a_2,…,a_s$线性无关，$a_1,a_2,…,a_s,\beta$线性相关$\Leftrightarrow\beta$可由$a_1,a_2,…,a_s$唯一表示
- 若m>n（向量的个数大于向量的维数），m个n维向量一定相关
向量组的秩
极大线性无关组：
若$a_1,a_2,\alpha_3,\alpha_4,a_5$中的部分组$\alpha_1,\alpha_2$线性无关且每个向量均可由$\alpha_1,\alpha_2$表示，则$\alpha_1,\alpha_2$为极大无关组
向量组的秩：极大无关组含向量个数
- $0\le r(a_1,a_2,…,a_s)\le min\{向量的个数，向量的维数\}$
- $a_1,a_2,…,a_s$线性无关$\Leftrightarrow r=s$
- $a_1,a_2,…,a_s$线性相关$\Leftrightarrow r<s$
行秩：矩阵中的行向量组的秩
列秩：矩阵中列向量组的秩
定理：行秩=列秩=$r(A)$（矩阵的秩）
$r(AB)\le min\{r(A),r(B)\}$
初等行变换不改变矩阵列向量组的线性关系
