本节主要介绍了矩阵的基本概念、伴随矩阵、逆矩阵、分块矩阵、初等变换以及矩阵的秩
矩阵概念
矩阵的定义:由一些数构成的$m\times n$的数表
矩阵和行列式的区别:
| | 行列式 | 矩阵 |
| —— | ————————- | ———————————— |
| 本质 | 一个数 | 数表 |
| 符号 | | | | [ ]或( ) |
| 形状 | 行数=列数,是方形 | 行数$\neq$列数(也可等) |方阵:矩阵中若行数=列数,则称为n阶方阵$A_{n\times n}\,or\,A_n$
单位阵$E$:主对角线上的数均为1,其余均为0,单位阵一定是方阵
同形矩阵:行列数均相等的矩阵,两个矩阵相等的前提必须是同形矩阵
矩阵运算
1.矩阵加减法
- 矩阵的加减法:将两个矩阵中对应的元素相加减,必须是同形矩阵才能相加减
2.矩阵乘法
- 矩阵的数乘运算:
- 一个数乘以一个矩阵,是这个数乘以这个矩阵的所有元素
- 矩阵所有元素均有公因子,这个公因子朝外提一次
- 矩阵的乘法:
- 前提条件:第一个矩阵的列数=第二个矩阵的行数
- 结果矩阵形状:结果矩阵的行数=第一个矩阵的行数,结果矩阵的列数=第二个矩阵的列数
- 矩阵$AB\ne BA$,$AB$有意义时,$BA$不一定有意义
- 矩阵$AB$相乘时,称$A$左乘$B$,$B$右乘$A$
- 若$AB=0$,并不意味着$A=0\,or\,B=0$
- 若$AB=AC,A\ne0$,并不意味着$B=C$
- 与零矩阵相乘都等于0,但得注意必须是同形矩阵
- 与单位阵$E$相乘:$AE=A,EB=B$
- 结合率:$(AB)C=A(BC)$
- 分配律:$(A+B)C=AC+BC\quad C(A+B)=CA+CB$
3.矩阵的幂
矩阵的幂:
求幂运算,A必须是方阵
$A^0=E$
- $A^{k_1}A^{k_2}=A^{k_1+k_2}$
- $(A^{k_1})^{k_2}=A^{k_1k_2}$
- $(AB)^k\ne A^kB^k$
- $(A+B)^2\ne A^2+2AB+B^2$
- $(A+E)^2=A^2+2AE+E^2$
矩阵的转置:
- 行列交换
- 若$A_{m\times n}$,则$A^T=A_{n\times m}$
- $((A)^T)^T=A$
- $(A+B)^T=A^T+B^T$
- $(kA)^T=kA^T$
- $(AB)^T=B^TA^T$
特殊的矩阵
1.对角线矩阵
对一个矩阵,左乘对角形矩阵,其结果相当于矩阵中每行元素乘以对角形矩阵中的数
对一个矩阵,右乘对角形矩阵,其结果相当于矩阵中每列元素乘以对角形矩阵中的数
对角形矩阵既是上三角矩阵又是下三角矩阵
2.对称矩阵
$a_{ij}=a_{ji}$:
若A、B是同阶对称,则:
- $A^T=A,B^T=B$
- $(A+B)^T=A^T+B^T=A+B$
- $(kA)^T=kA^T=kA$
- $(AB)^T=B^TA^T=BA\neq AB$
- 若AB的结果依旧是对称矩阵,则A、B是可交换的
反对称矩阵:
- 主对角线全为0,$a_{ij}=-a_{ji}$
$A^T=-A$
伴随矩阵
方阵的行列式:
- 方阵行列式的性质:
- $|A^T|=|A|$
- $|kA|=k^n|A|$
- $|AB|=|A||B|$
- 方阵行列式的性质:
伴随矩阵:
求所有元素的代数余子式
按行求得代数余子式按列放,构成的矩阵$A^*$为伴随矩阵
伴随矩阵的相关定理:
- 对任意方阵A:$AA^=A^A=|A|E$
- 若方阵$|A|\ne 0$,则$|A^*|=|A|^{n-1}$
逆矩阵
1.基本概念
- 定义:若A是n阶方阵,且存在n阶方阵B,使得$AB=BA=E$,则A可逆,称B为A的逆矩阵,即$B=A^{-1}$
- 相关性质:
- 未必所有方阵均可逆
- 若存在逆矩阵,那么逆矩阵唯一
- 相关定理:A可逆的充要条件为$|A|\ne 0$,则此时$A^{-1}=\frac{1}{|A|}A^*$
- 推论:若A、B是n阶方阵,存在$AB=E(BA=E)$,则A可逆,且$A^{-1}=B$
2.逆矩阵性质
- 若A可逆,那么$A^{-1}$也可逆,即$(A^{-1})^{-1}=A$
- 若A、B均可逆,那么AB均可逆,且$(AB)^{-1}=B^{-1}A^{-1}$
- 若A可逆,则$A^T$也可逆,且$(A^T)^{-1}=(A^{-1})^T$;若$k\ne 0$,则$(kA)^{-1}=\frac1kA^{-1}$
- 若A可逆,则$|A^{-1}|=|A|^{-1}$
- 若A可逆,则$A^$也可逆,且$(A^)^{-1}=\frac1{|A|}A$
分块矩阵
标准形矩阵:从左上角开始的一串1,串中1不能间断,不一定是方阵
分块矩阵的乘法与基本矩阵乘法一致,前提是可乘
初等变换
初等变换包括:
- 交换两行(列)
- 用$k(k\ne 0)$乘以某行(列)
- 用某行(列)乘以一个数加到另一行(列)上去
任给一个矩阵都可以通过初等变换化成标准形
等价:由矩阵A经初等变换得到B,即称A等价于B
- 对称性:若A等价于B,则B也等价于A
- 传递性:若A等价于B,B等价于C,则A也等价于C
1.初等方阵
初等方阵:对单位阵E做一次初等变换得到的矩阵
- 交换两行的初等方阵:$|E(i,j)|=-1$
- 行乘以某数的初等方阵:$|E(i(k)|=k(k\ne 0)$
- 行乘以某数加到某行的初等方阵:$|E(i,j(k))|=1$
初等方阵的相关性质:
初等方阵均可逆:
其逆矩阵和转置矩阵均为初等方阵
若A可逆,那么其充分必要条件是A的标准形为E
若A可逆,那么其充分必要条件是A=一些初等方阵的乘积
2.初行变换法求逆
- 只做初等行变换,使得:
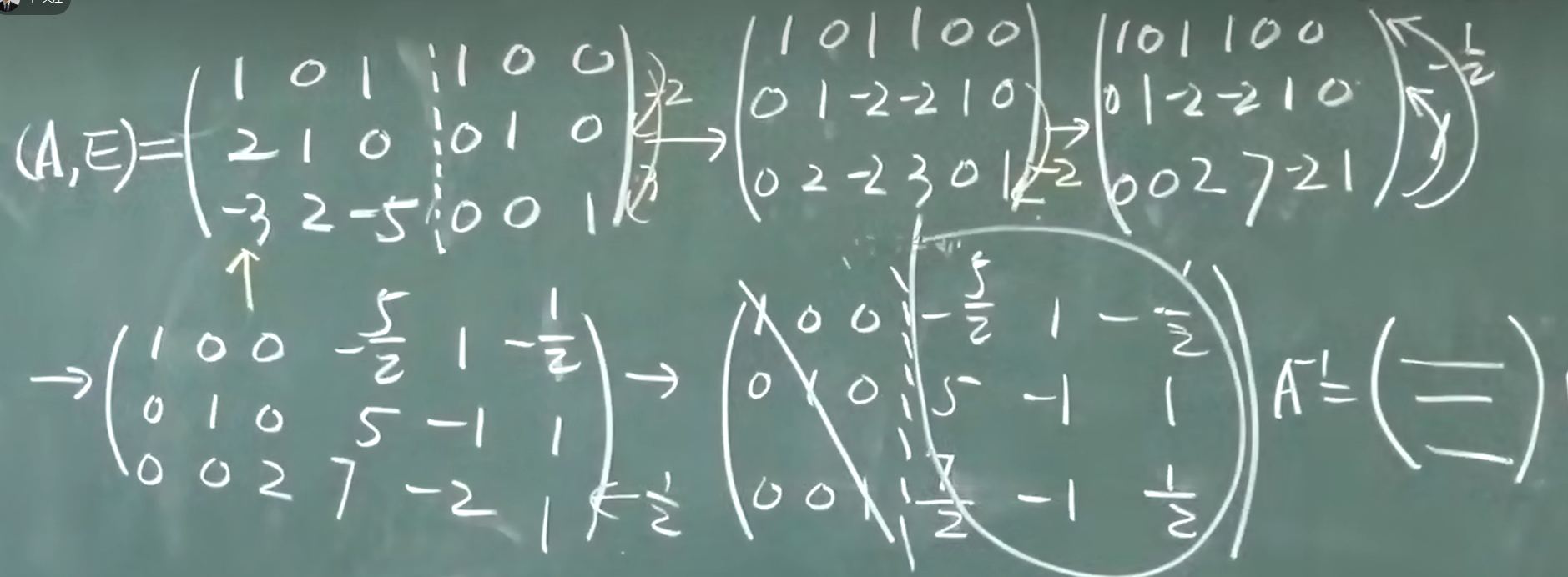
矩阵的秩
- 定义:非零子式的最高阶数,记$r(A)=r$
- 有矩阵$A_{m\times n}$,则有$0\le r(A)\le min\{m,n\}$
- 满秩:$r(A)= min\{m,n\}$
- 降秩:$r(A)<min\{m,n\}$
- 若A为方阵,有A满秩$\Leftrightarrow$A可逆
- $r(A)=r\Leftrightarrow$有一个r阶子式不为0,所有r+1阶子式为0
1.阶梯形
定义:
- 若有零行,零行在非零的下边
- 左起首非零元左边零个数随行数增加而严格增加
2.简化阶梯形
- 非零行的首非零元是1
- 首非零元所在列的其余元素是0
3.秩相关的定理与性质
初等变换不改变秩
r(A)=阶梯形非零行的行数
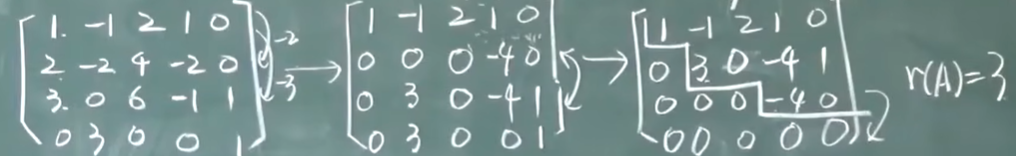
$r(A)=r(A^T)$
任意矩阵乘以可逆矩阵,其秩不变
有矩阵$A_{m\times n}$,P为m阶可逆方阵,Q为n阶可逆方阵
