本节主要介绍了流水线的相关基础知识
流水线基本概念
1.流水线的特点
- 流水过程由多个相关的子过程组成,这些子过程称为流水线的“级”或“段”,“段”的数目称为流水线的“深度”
- 每个子过程由专用的功能段实现
- 各功能段的时间应基本相等,通常为1个时钟周期(1拍)
- 流水线需要经过一定的通过时间才能稳定
- 流水技术适合于大量重复的时序过程
2.流水线的分类
按流水线所完成的功能分类:
单功能流水线,是指只能完成一种固定功能的流水线
多功能流水线,是指各段可以进行不同的连接,从而完成不同的功能
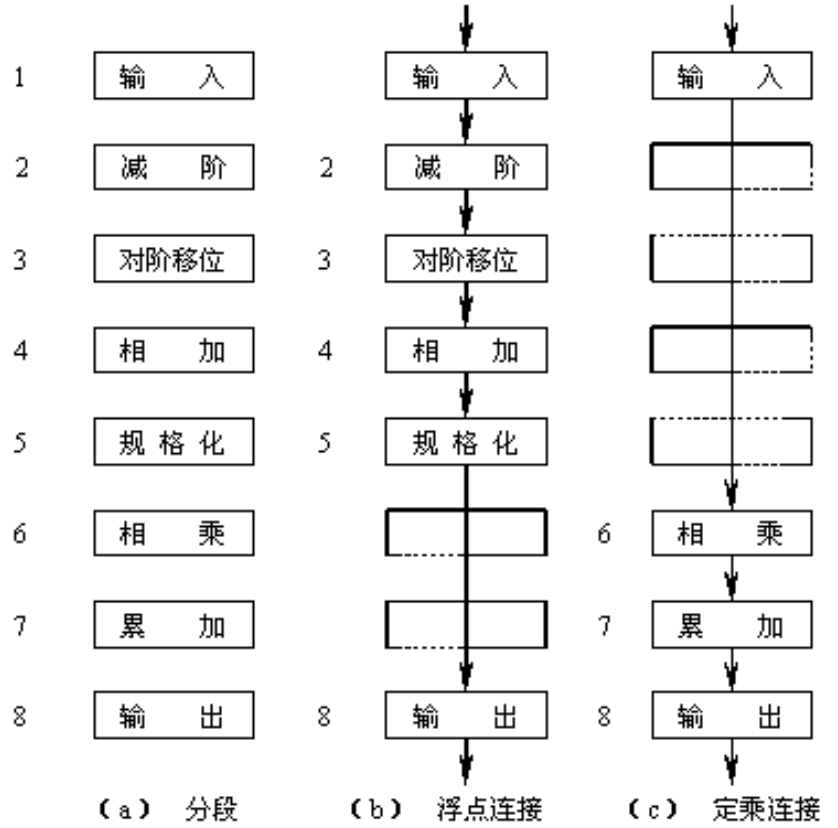
按同一时间内流水线的连接方式划分
- 静态流水线,是指在同一时间内,流水线的各段只能按同一种功能的连接方式工作
- 动态流水线,是指在同一时间内,当某些段正在实现某种运算时,另一些段却在实现另一种运算
按流水的级别划分
- 部件级流水线,又叫运算操作流水线,是把处理机的算术逻辑部件分段,使得各种数据类型的操作能够进行流水
- 处理机级流水线,又叫指令流水线,是把解释指令的过程按照流水方式处理
- 处理时间流水线,又叫宏流水线,是由两个以上的处理机串行地对同一数据流进行处理,每个处理机完成一项任务
按照数据表示来进行分类
- 标量流水处理机,是指处理机不具有向量数据表示,仅对标量数据进行流水处理
- 向量流水处理机,是指处理机具有向量数据表示,并通过向量指令对向量的各元素进行处理
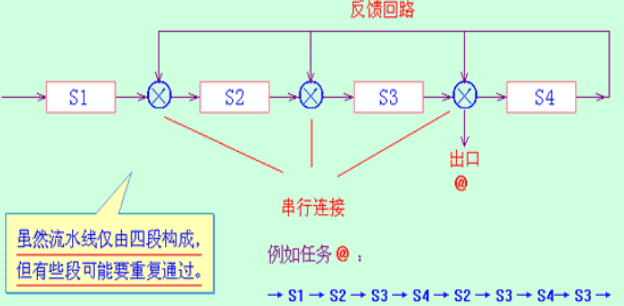
按照是否有反馈回路来进行分类
线性流水线,是指流水线的各段串行连接,没有反馈回路
非线性流水线,是指流水线种除有串行连接的通路外,还有反馈回路
- 但其存在流水线调度问题
- 确定什么时候向流水线引进新的输入,从而使新输入的数据和先前操作的反馈数据流水线中不产生冲突,此即所谓流水线调度问题
MIPS基本流水线
1.实现MIPS指令的一种简单数据通路
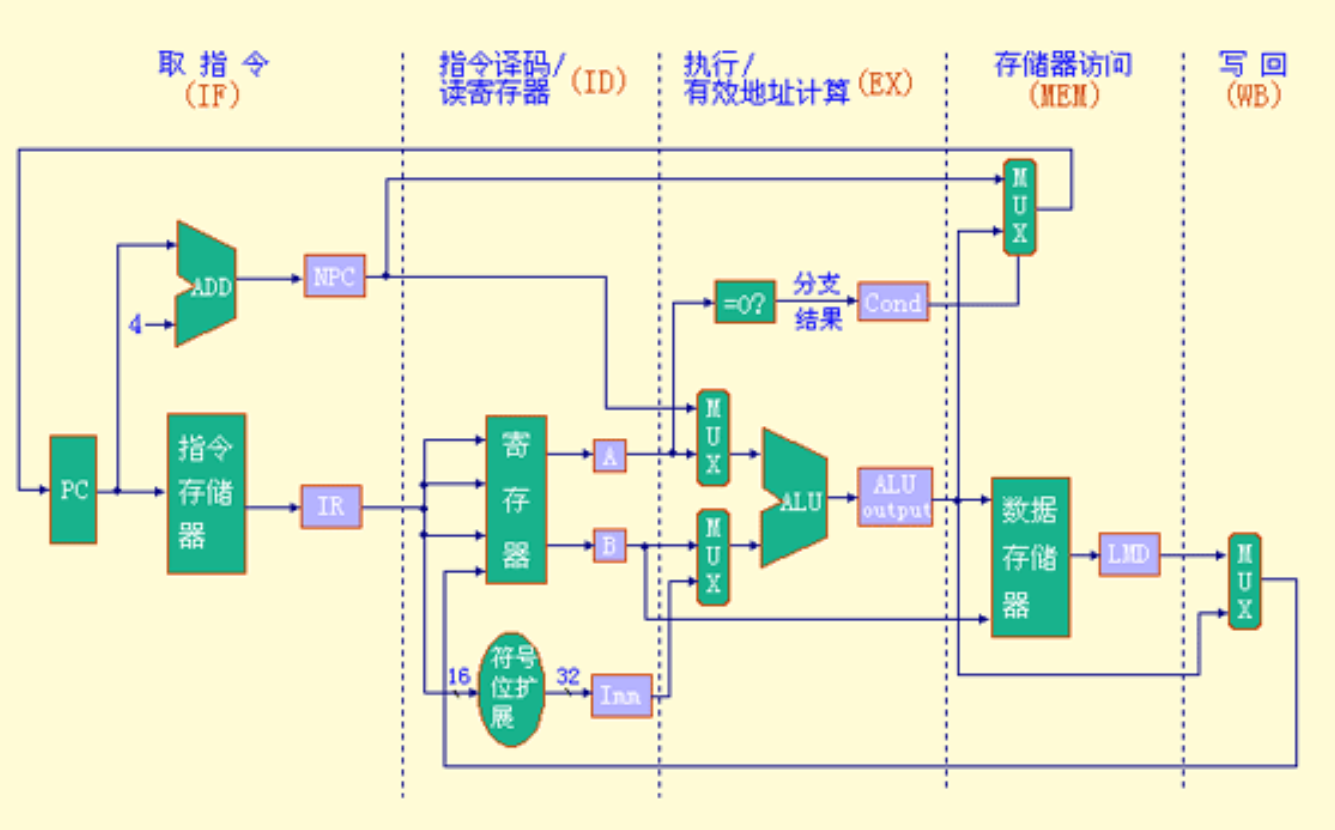
这是一种非流水方式
将指令执行划分为5个阶段:
取指令周期(IF)
根据PC值从存储器中取出指令,并将指令送入指令寄存器IR,PC值增加4,指向顺序的下一条指令,
并将下一条指令的地址放入临时寄存器NPC中
指令译码/读寄存器周期(ID)
进行指令译码,读取IR寄存器(指令寄存器),按照相应寄存器号读寄存器文件,并将读出结果放入两个临时寄存器A和B中
同时对IR寄存器中内容的低16位进行符号扩展,然后将符号扩展后的32位立即值保存在临时寄存器Imm中
执行/有效地址计算周期(EX)
- 存储器访问:$ALUoutput\leftarrow A+Imm$
- 寄存器-寄存器ALU:$ALUoutput\leftarrow A\,op\,B$
- 寄存器-立即数ALU:$ALUoutput\leftarrow A\, op\, Imm$
- 分支操作:$ALUoutput\leftarrow NPC+Imm\quad Cond\leftarrow (A\,op\, 0)$
存储器访问/分支完成周期(MEM)
访问操作:
- $Load:\quad LMD\leftarrow LMDMEN[ALUoutput]$
- $Store:\quad Mem[ALUoutput]\leftarrow B$
分支操作:
写回周期(WB)
- 寄存器-寄存器型ALU指令:$Reg[IR_{16..20}]\leftarrow ALUoutput$
- 寄存器-立即值型ALU指令:$Reg[IR_{11..15}]\leftarrow ALUoutput$
- Load指令:$Reg[IR_{11..15}]\leftarrow LMD$
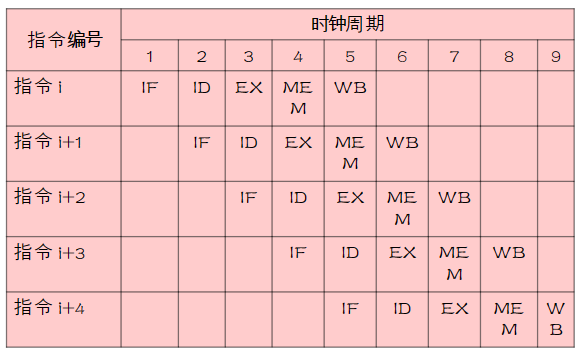
2.一种简单的MIPS流水线
数据通路中的每一个周期成为流水线的一段
每个时钟周期启动一条指令
实现流水技术应解决的一些问题
- 应保证流水线各段不会在同一时钟周期内使用相同的寄存器通路资源
- PC计算问题:为了能够在每个时钟周期启动一条新的指令,流水线必须在IF段获取下一条指令的地址,并将其保存在PC中
- 合理划分流水段,每段内的操作必须在一个时钟周期内完成
- 流水线寄存器设计:为防止寄存器中的值在为流水线中某条指令所用时被流水线中其他的指令所重写,可在流水线各段时间设置流水线寄存器文件,也称锁存器
流水线性能分析
1.吞吐率
是衡量流水线速度的重要指标
吞吐率:是指单位时间内流水线所完成的任务数或输出结果的数量
最大吞吐率$TP_{max}$:是指流水线在达到稳定状态后所得到的吞吐率
假设流水线各段的时间相等,均为$\Delta t_0$,则:
假设流水线各段的时间不相等,第i段的时间为$\Delta t_i$,则:
最大吞吐率取决于流水线中最慢一段所需要的时间,该段为流水线的瓶颈
实际吞吐率$TP$:设流水线由m段组成,完成n个任务的吞吐率称为实际吞吐率
若各段时间相等(假设均为$\Delta t_0$),则完成时间:
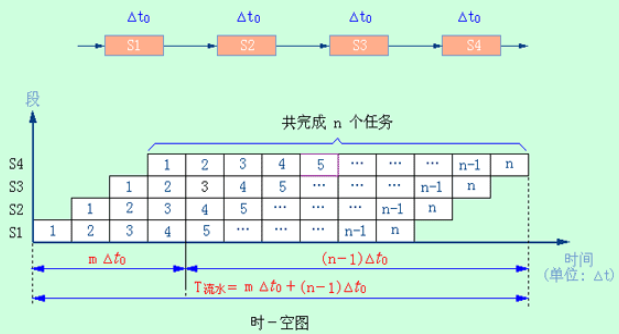
则实际吞吐率为:
若各段时间不等(假设第i段为$\Delta t_i$),且假设$\Delta t_j=max{\Delta t_i}$,则完成时间:
则实际吞吐率为:
2.加速比
加速比S是指流水线速度与等功能的非流水线速度之比
若流水线为m段,每段时间均为$\Delta t_0$,则:
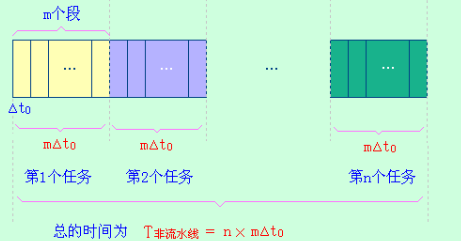
3.效率
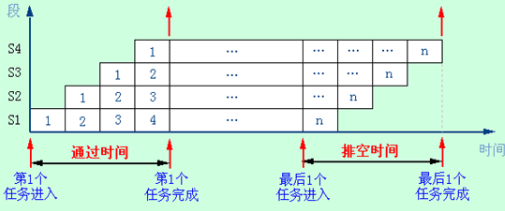
效率是指流水线的设备利用率
由于流水线有通过时间和排空时间,所以流水线的各段并非一直满负荷工作,E<1
若各段时间相等,则各段效率也相等,即e1=e2=e3……=$n\Delta t_0/T_{流水}$
整个流水线效率:
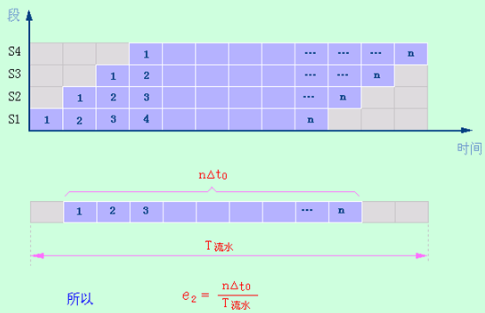
当$n>>m$时,$E\approx1$
4.吞吐率、加速比和效率的关系
效率是实际加速比S与最大加速比m之比
当$\Delta t_0$不变时,流水线的效率与吞吐率呈正比,为了提高效率而采取的措施,也有助于提高吞吐率
向量处理机
- 向量处理机:具有向量数据表示和相应向量指令的流水线处理机称为向量流水线处理机,也称向量处理机
