本节主要介绍了存储程序计算机、Amdahl定律、CPU的性能计算
存储程序计算机
存储程序计算机:
- 一种计算机系统设计模型
- 实现了一种通用图灵机
冯诺依曼描述的计算机由四个部分组成:
- 运算器:用于完成数值运算
- 存储器:用于存储数据和程序
- 输入/输出:用于完成计算机和外部的信息交流
- 控制器:根据程序形成控制(指令、命令)序列,完成对数据的运算
存储程序机器的结构:
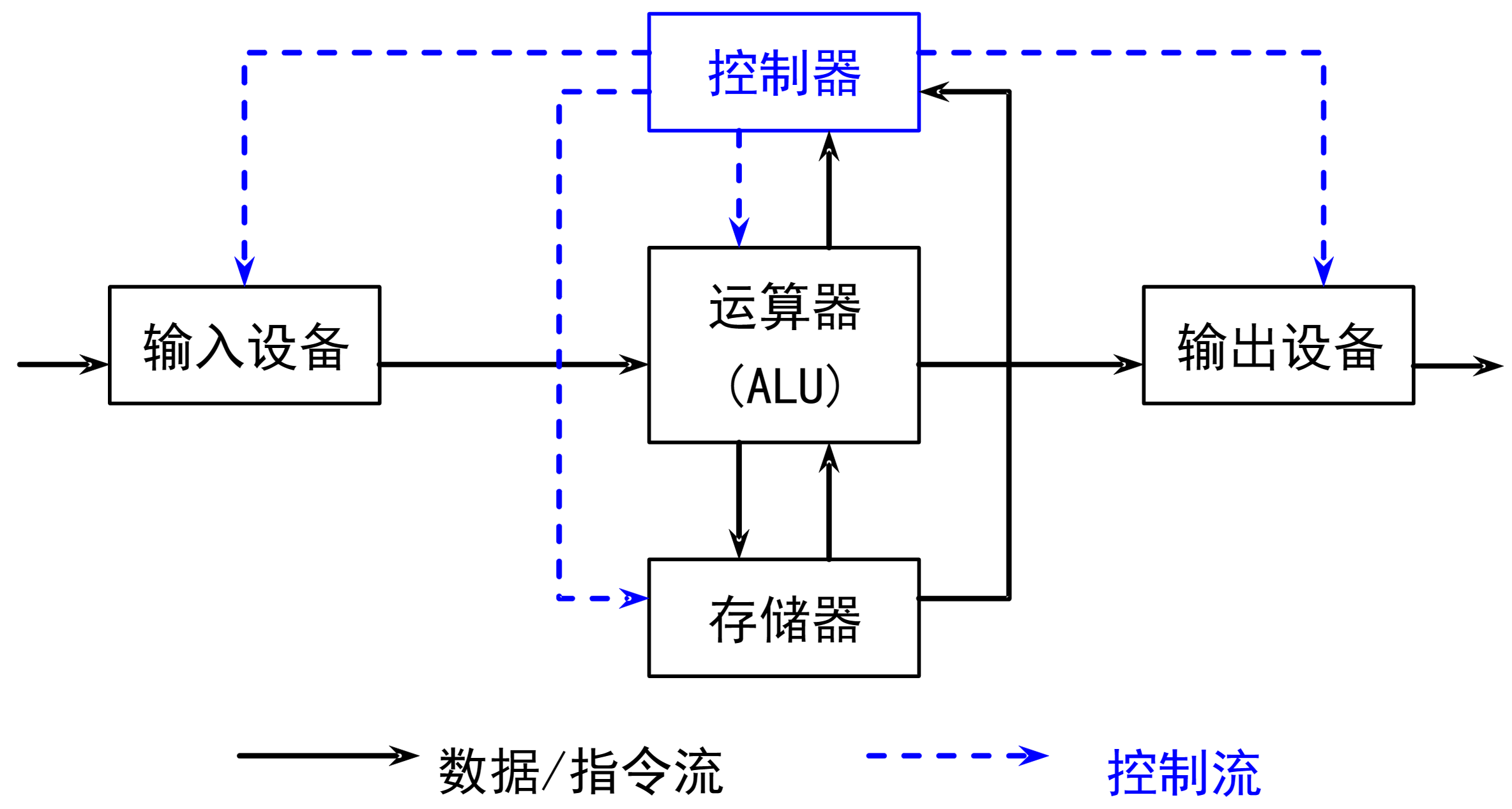
运算器与控制器以及寄存器组一起构成CPU
Amdahl定律
假设我们对机器(部件)进行某种改进,那么机器系统(部件)的加速比就是:
- 系统加速比告知改进后的机器比改进前快多少
系统加速比依赖于两个因素:
- 可改进比例:可改进部分在原系统计算时间中所占的比例,它总是小于等于1的:$\frac{T_1}{T_0}$
- 部件加速比:可改进部分改进以后的性能提高,一般情况下它是大于1的:$\frac{T_1}{T_2}$
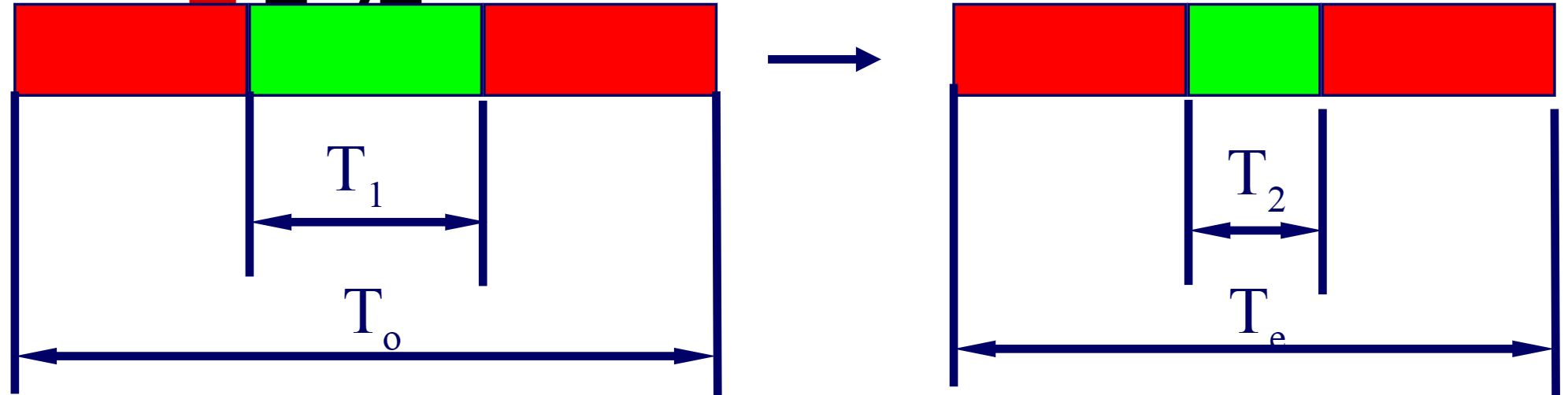
Amdahl的系统执行时间:部件改进后,系统的总执行时间等于不可改进部分的执行时间加上可改进部分改进后的执行时间,即:
故Amdahl的系统加速比:
Amdahl定律的观点
- 性能增加的递减规则:仅仅对计算机中的一部分做性能改进,则改进越多,系统获得的效果越小
- Amdahl定律的一个重要推论:针对整个任务的一部分进行优化,则最大加速比不大于$\frac{1}{1-可改进比例}$
- Amdahl定律衡量一个”好”的计算机系统:具有高性能价格比的计算机系统是一个带宽平衡的系统,而不是看它使用的某个部件的性能
CPU的性能计算
程序执行过程中所处理的指令数,记为IC
每条指令执行所需要的时钟周期数CPI
每条指令执行所需要的平均时钟周期数:
- $CLK$表示总共的周期数
假设计算机系统由$n$种指令,其中第$i$种指令的处理周期数为$CPI_i$,在程序中第$i$种指令出现的次数为$IC_i$
