本节主要介绍了Transformer模型的一些基本概念
Transformer模型的基本概念
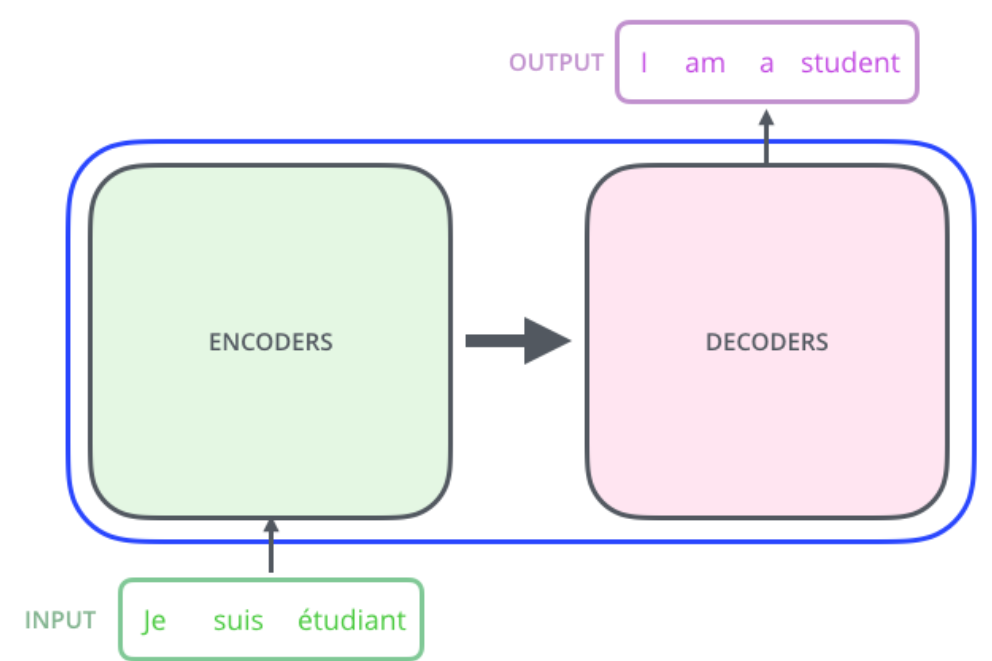
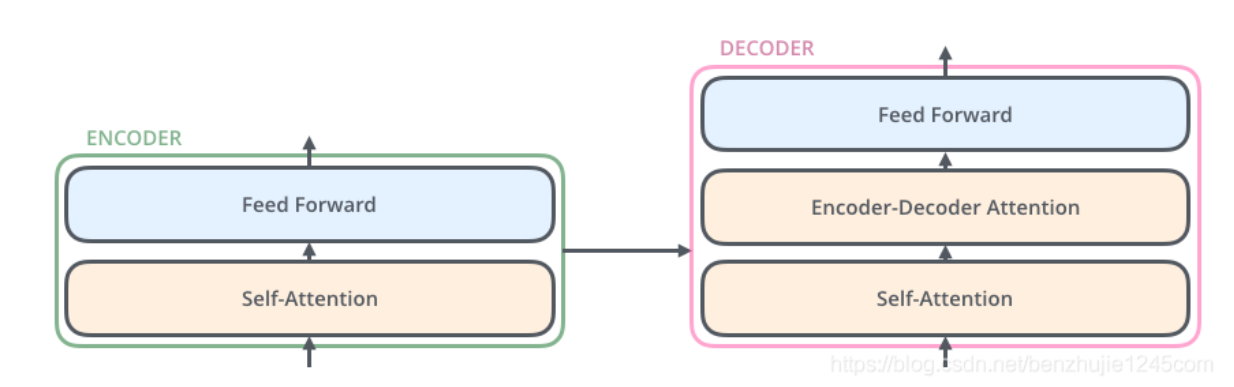
Transformer 本质上是一个 Encoder-Decoder 架构。因此中间部分的 Transformer 可以分为两个部分:编码组件和解码组件
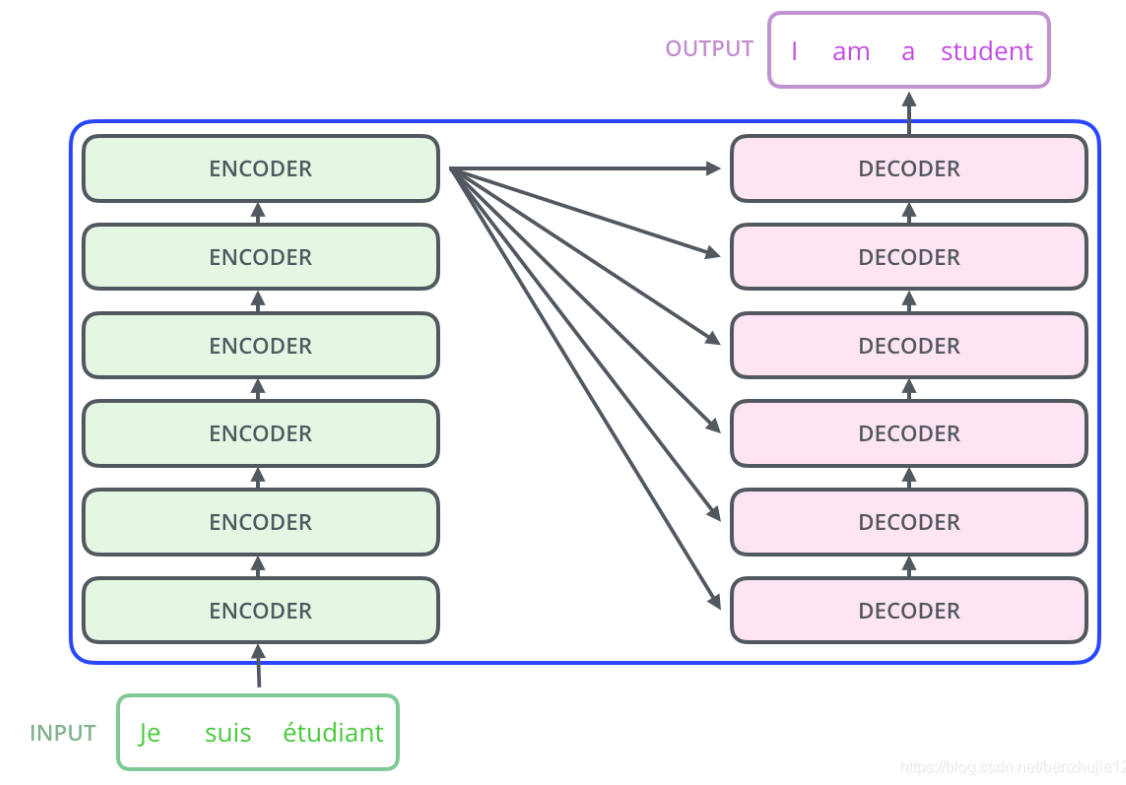
其中,编码组件由多层编码器(Encoder)组成(在论文中作者使用了 6 层编码器,在实际使用过程中你可以尝试其他层数),解码组件也是由相同层数的解码器(Decoder)组成(在论文也使用了 6 层)
每个编码器由两个子层组成:Self-Attention 层(自注意力层)和 Position-wise Feed Forward Network(前馈网络,缩写为 FFN),每个编码器的结构都是相同的,但是它们使用不同的权重参数
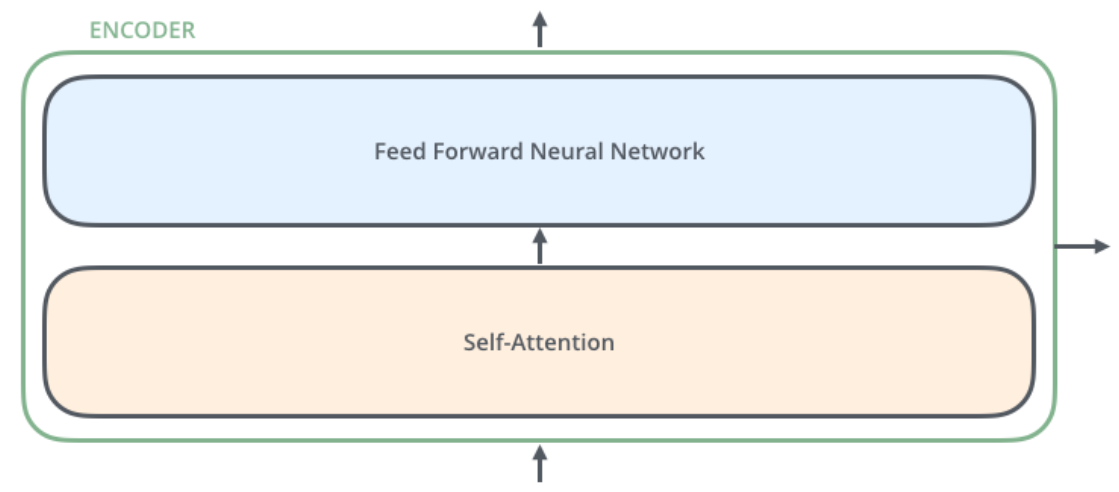
- 编码器的输入会先流入 Self-Attention 层。它可以让编码器在对特定词进行编码时使用输入句子中的其他词的信息(可以理解为:当我们翻译一个词时,不仅只关注当前的词,而且还会关注其他词的信息)
- 然后,Self-Attention 层的输出会流入前馈网络
解码器也有编码器中这两层,但是它们之间还有一个注意力层(即 Encoder-Decoder Attention),其用来帮忙解码器关注输入句子的相关部分(类似于 seq2seq 模型中的注意力)
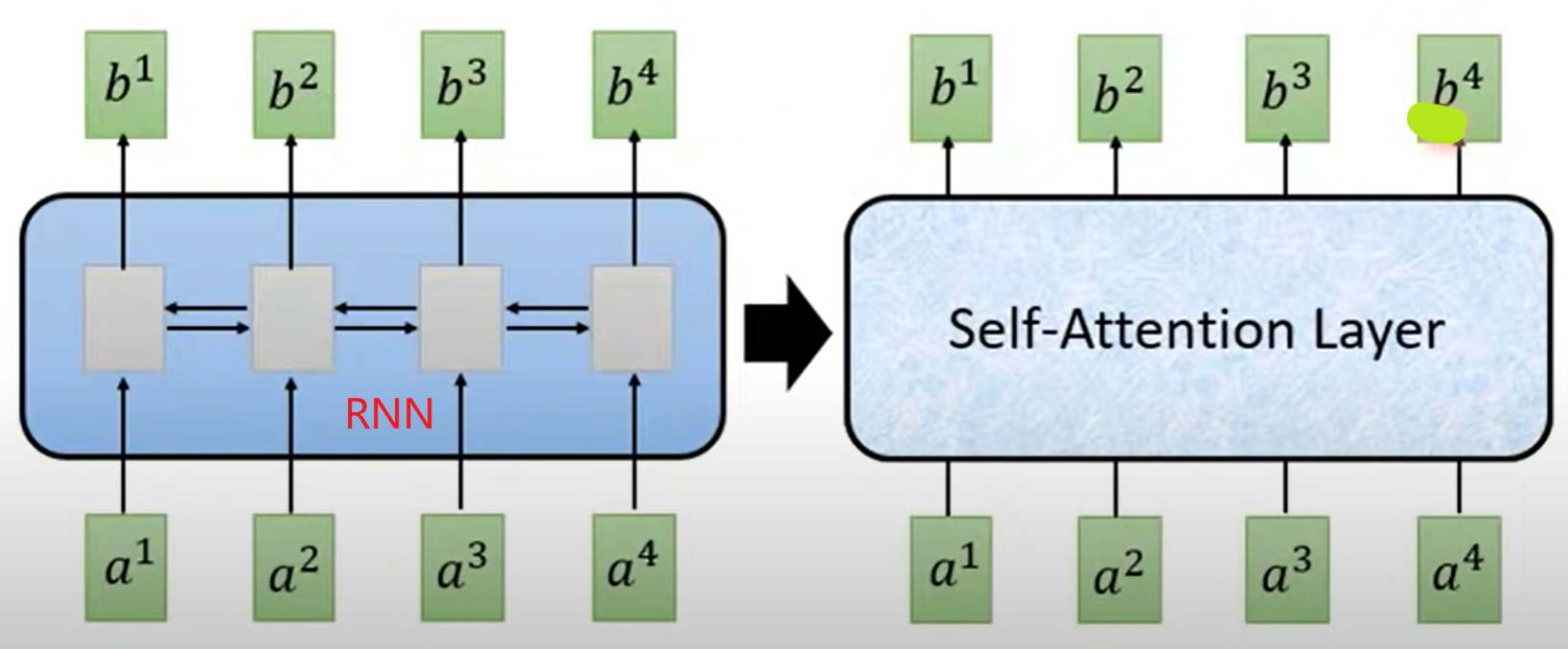
Self-attention(自注意力)
简单理解:使用self-attention取代RNN,使得$b^1,b^2,b^3,b^4$可以同时被计算出
1.计算步骤
计算词嵌入与$q,k,v$
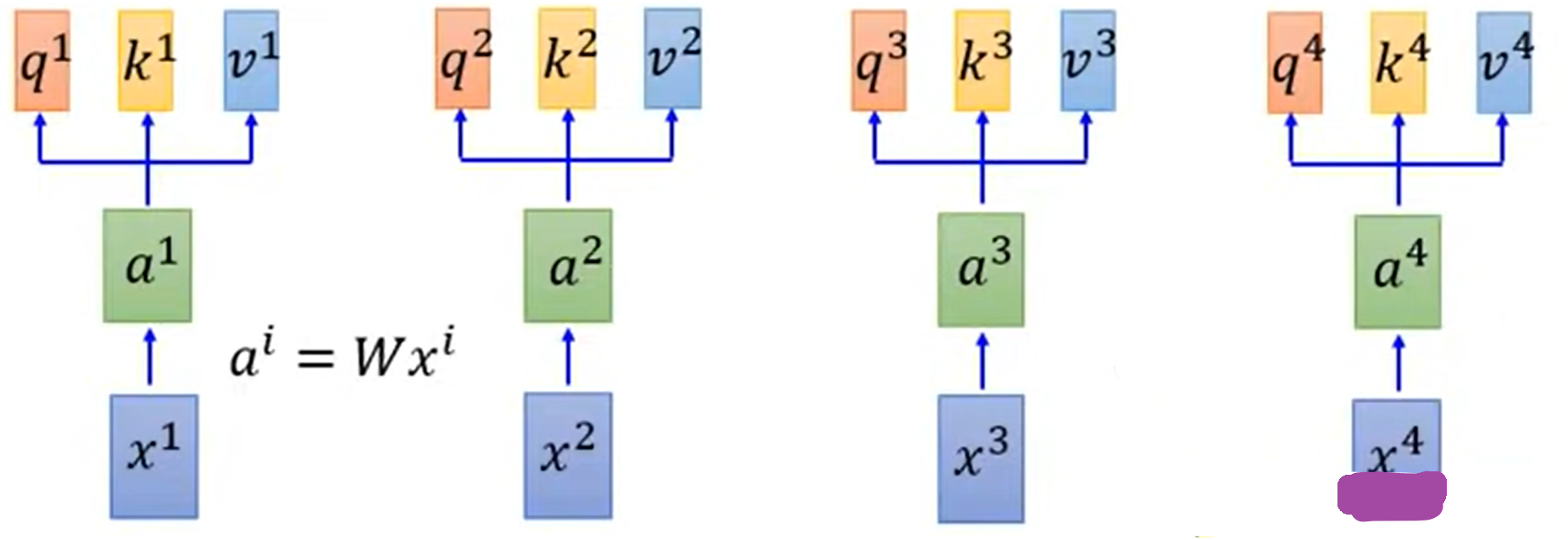
- $a^i=Wx^i$
- $q^i=W^qa^i$:q代表去匹配别的
- $k^i=W^ka^i$:k代表被匹配
- $v^i=W^va^i$:v代表被提取的信息
拿每个q与每个k做attention:
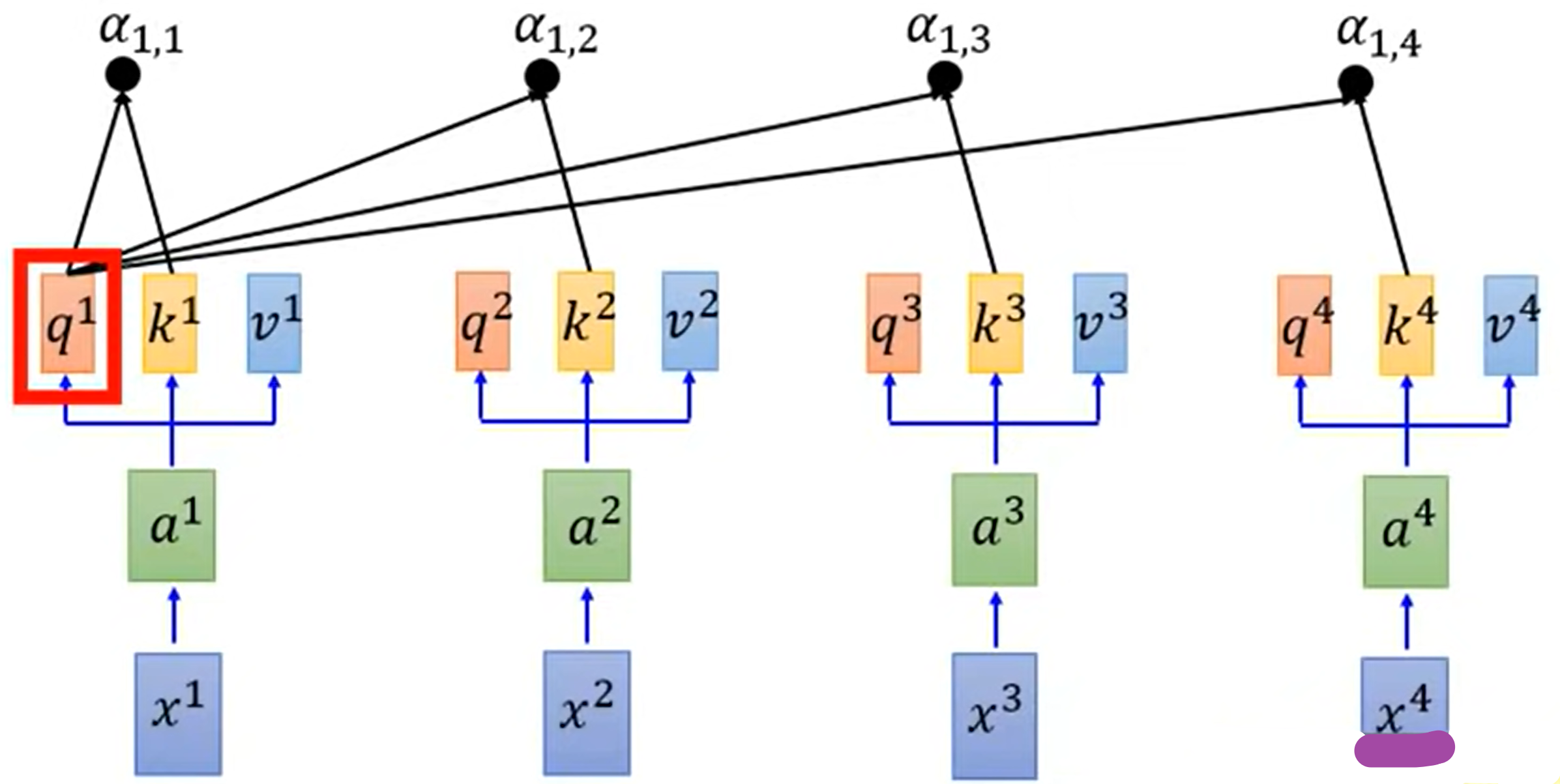
- $\alpha_{1,i}=\frac{q^1k^i}{\sqrt{d}}$,其中d为q,k的维度
对每一个attention做softmax
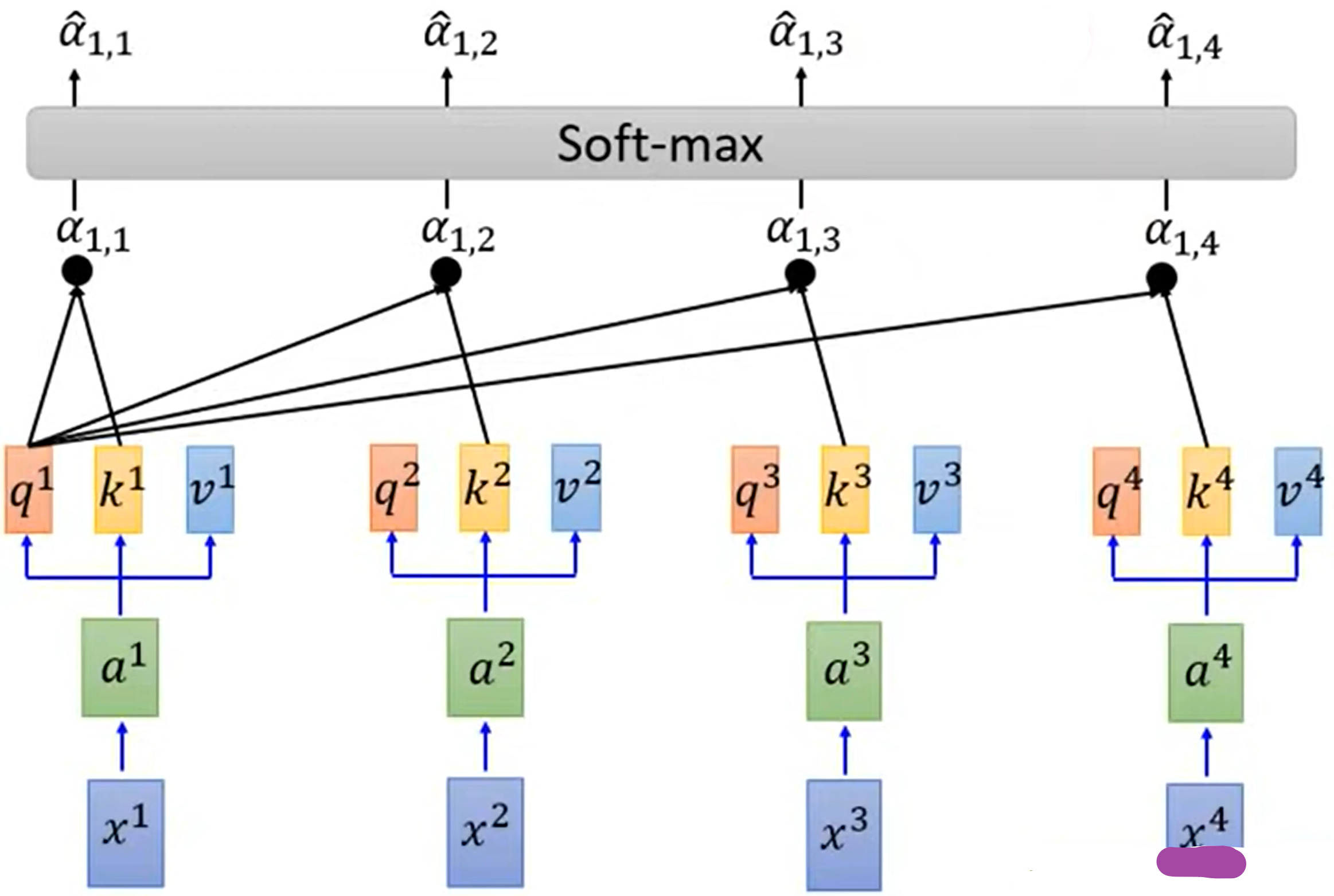
将每一个$\hat{\alpha}$与$v^1$计算相乘后求和
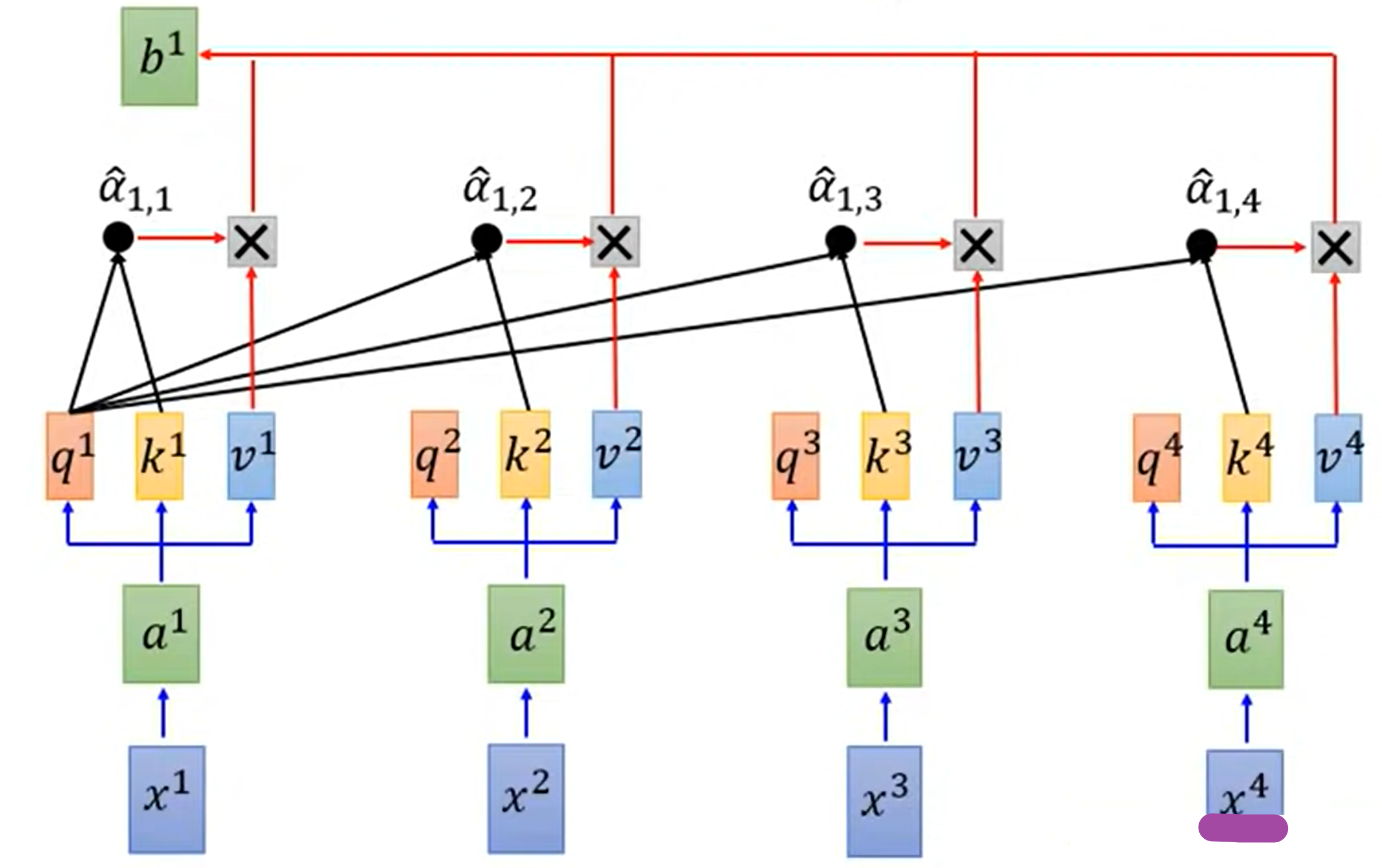
- $b^1=\sum \hat{\alpha}_{1,i}v^i$
同理,按上述步骤也可以算出$b^2,b^3,b^4$
2.平行化处理机制(矩阵处理)
- 求$Q,K,V$:
- 将$a^1,a^2,a^3,a^4$这四个列向量按列堆叠在一起组成一个矩阵$I$
- 将$I$分别与$W^q,W^k,W^v$矩阵相乘,就可以得到按列堆叠的向量$Q,K,V$
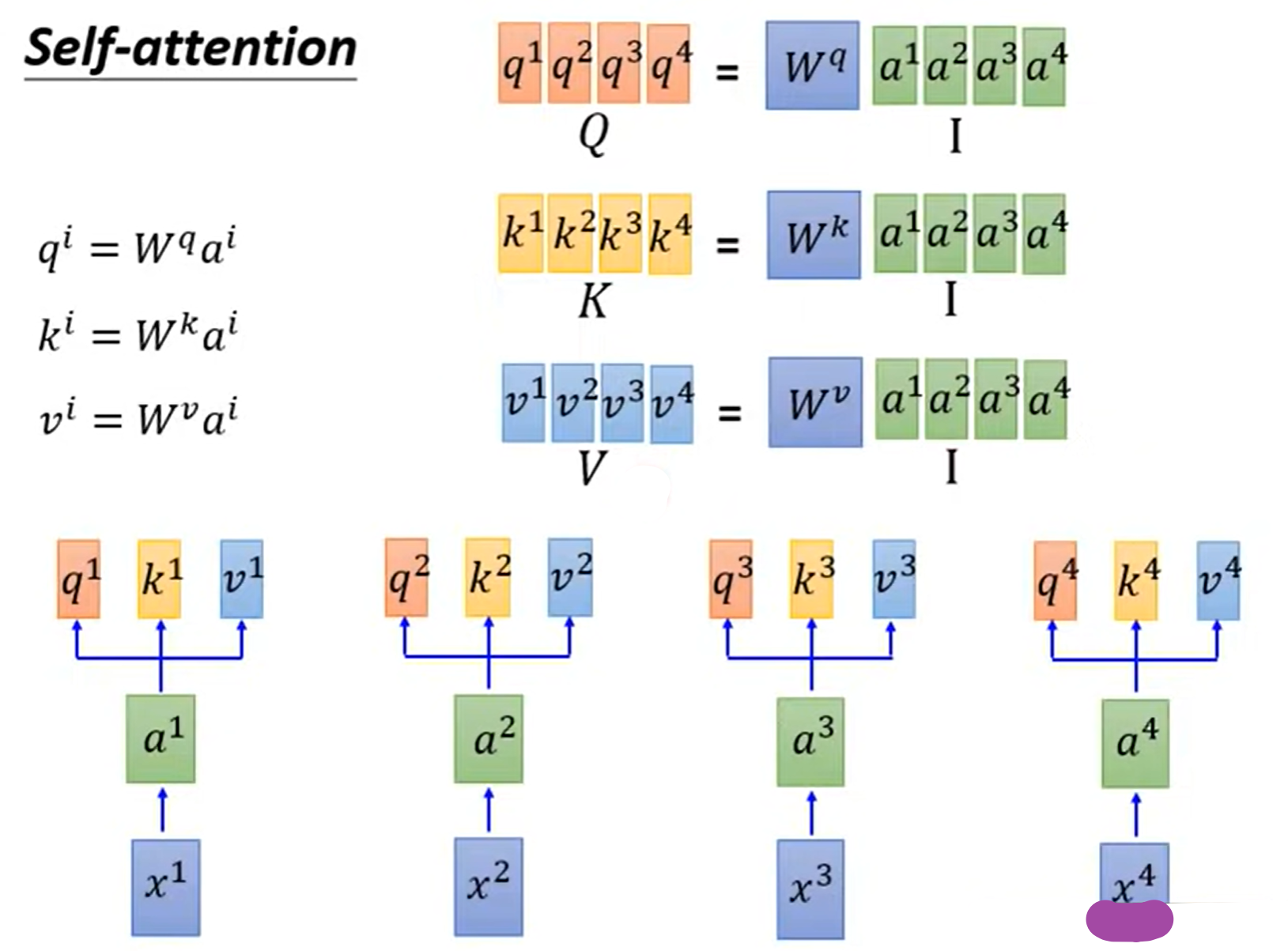
求所有attention:
- 将矩阵$K$转置后得到的$K^T$与Q进行矩阵相乘即可以得到每一个attention(这里计算忽略了除以$\sqrt{d}$
- 之后再对得到的attention矩阵$A$按列求softmax,得到矩阵$\hat{A}$
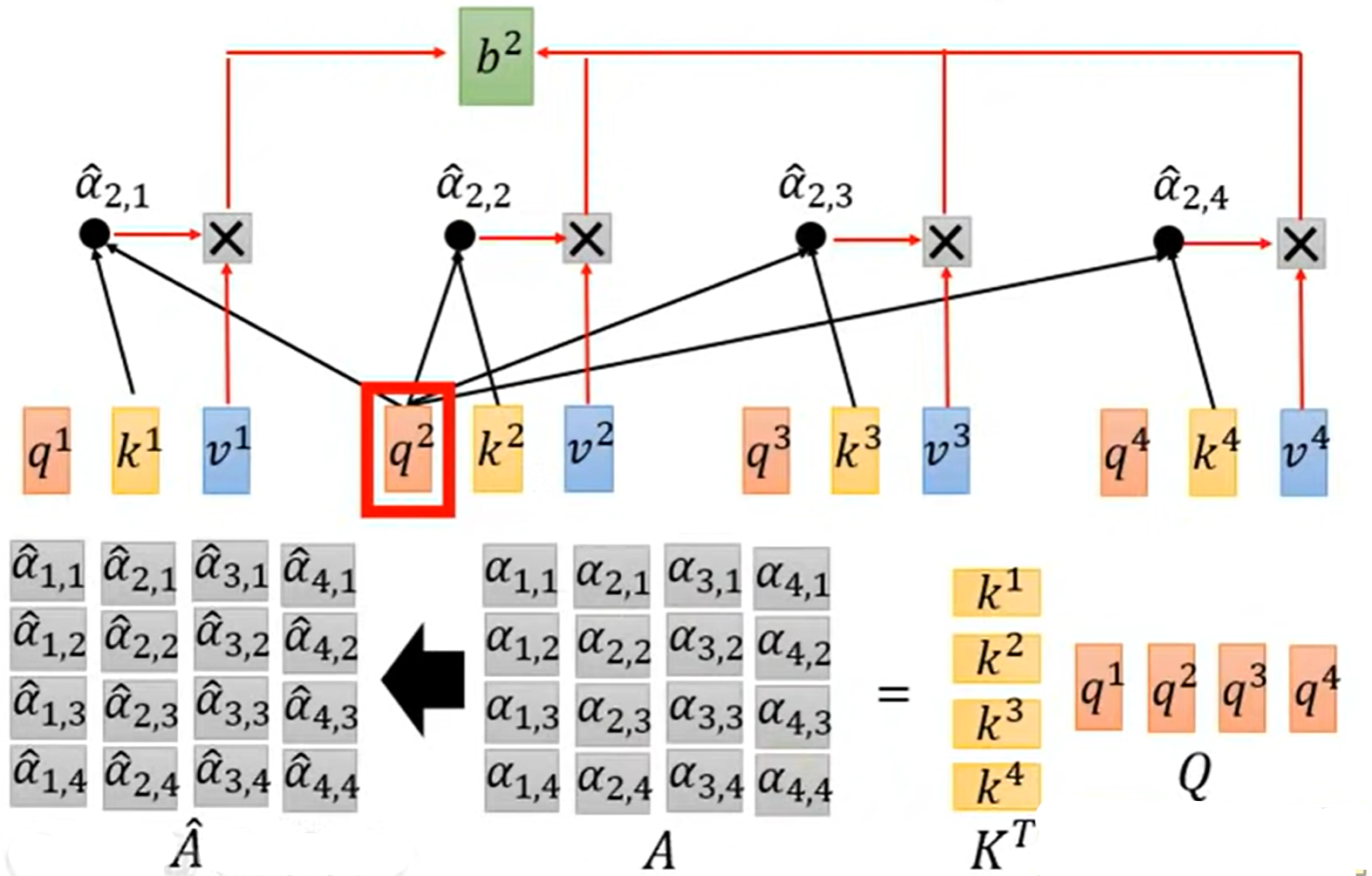
求输出$b^1,b^2,b^3,b^4$:
- 将矩阵$V$与$\hat{A}$相乘得到输出矩阵O
- 其中输出矩阵O就是输出列向量$b^1,b^2,b^3,b^4$按列的堆叠
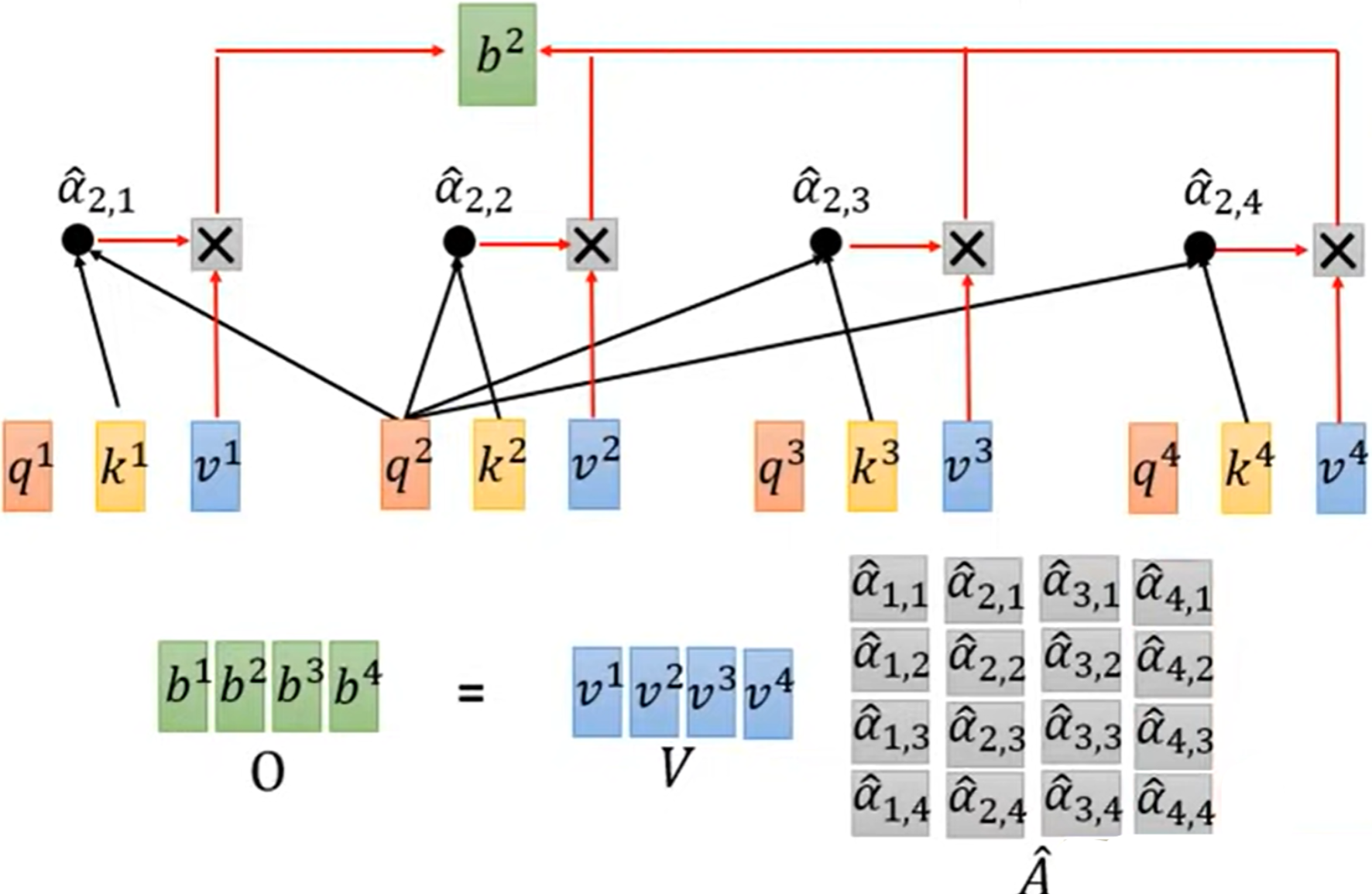
总结:
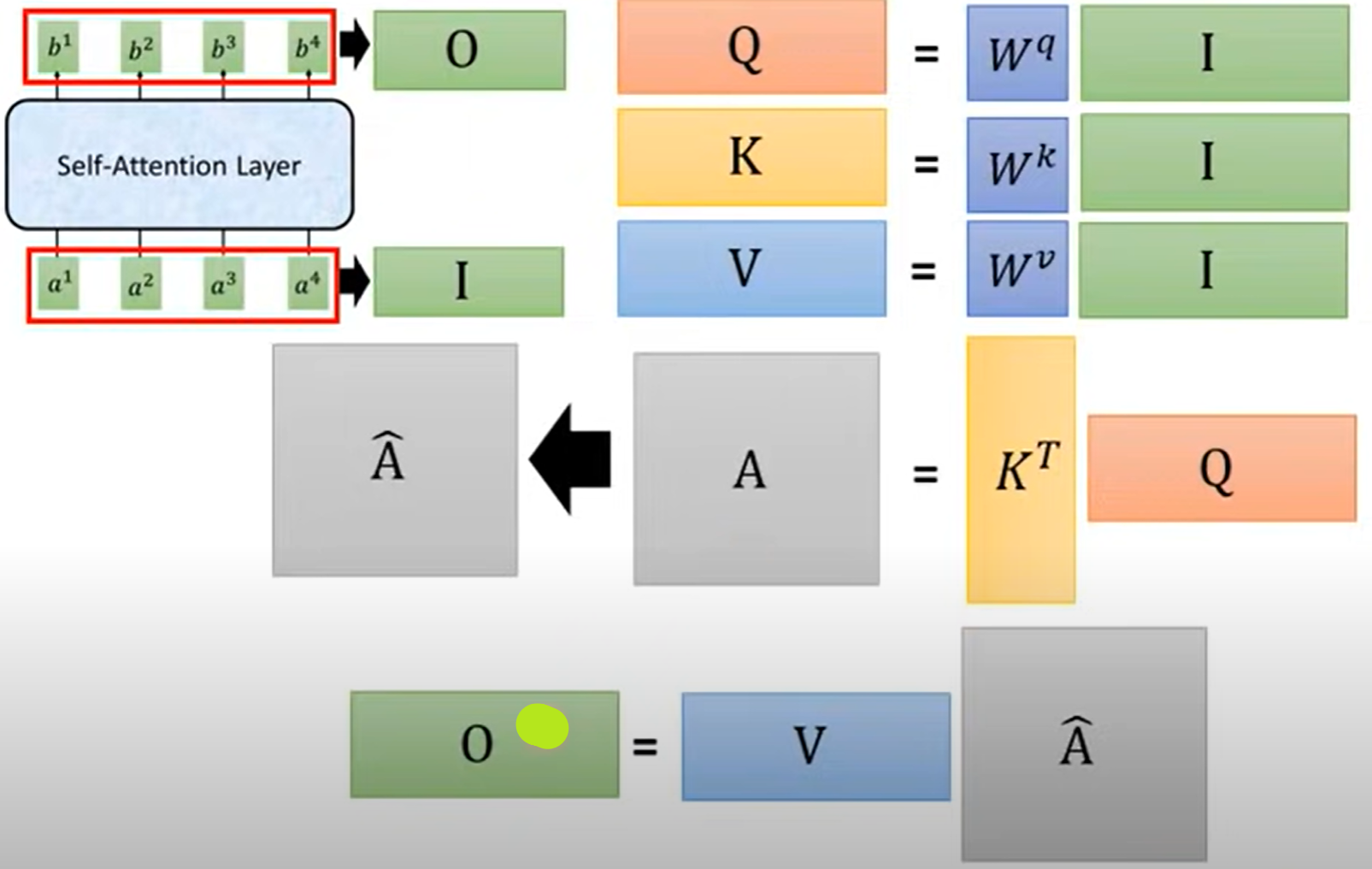
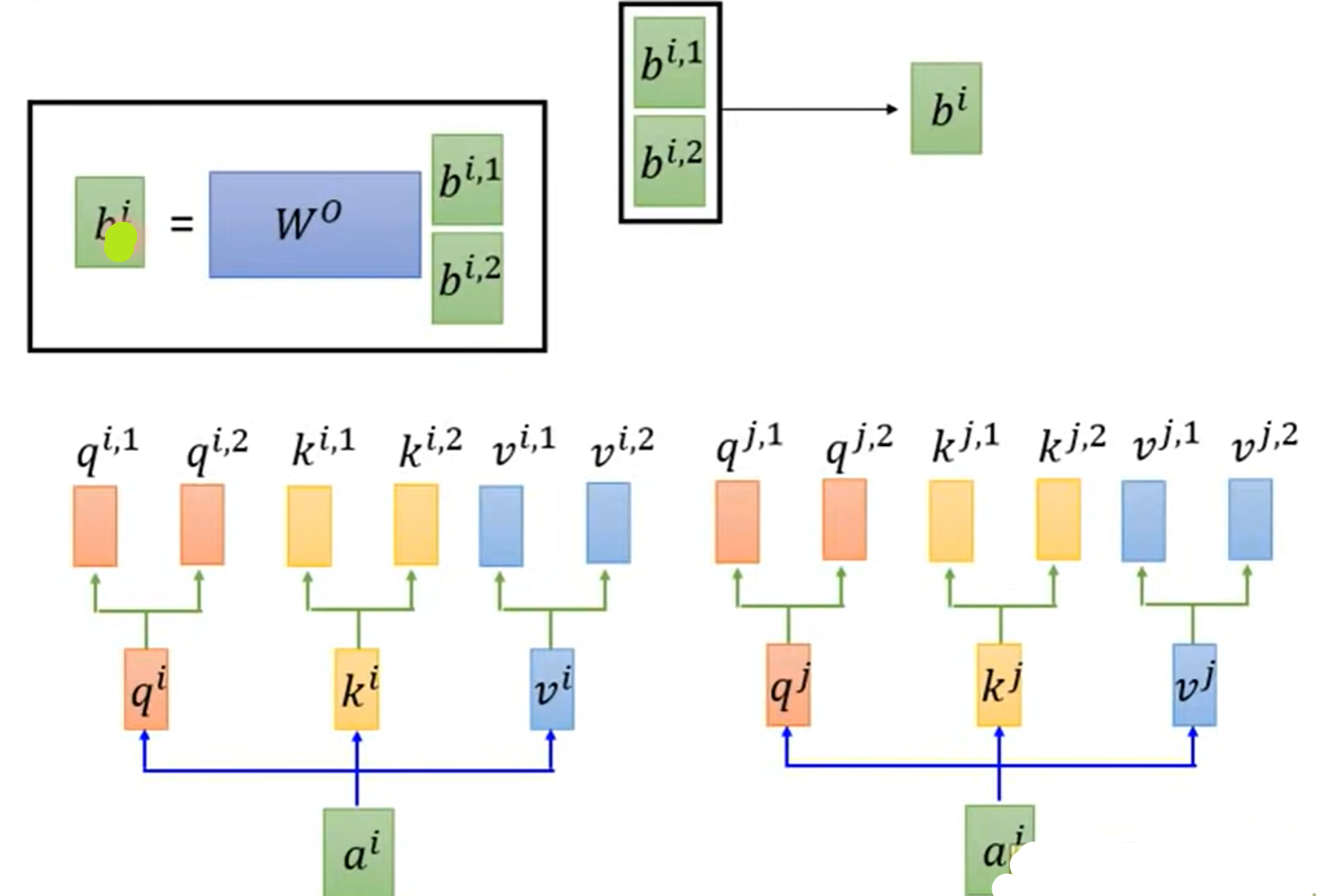
3.多头自注意力机制(Multi-head Self-attention)
- 每一个头只与对应相同系数的k做attention,即$q^{i,1}$只与$k^{i,1},k^{j,1}$相乘
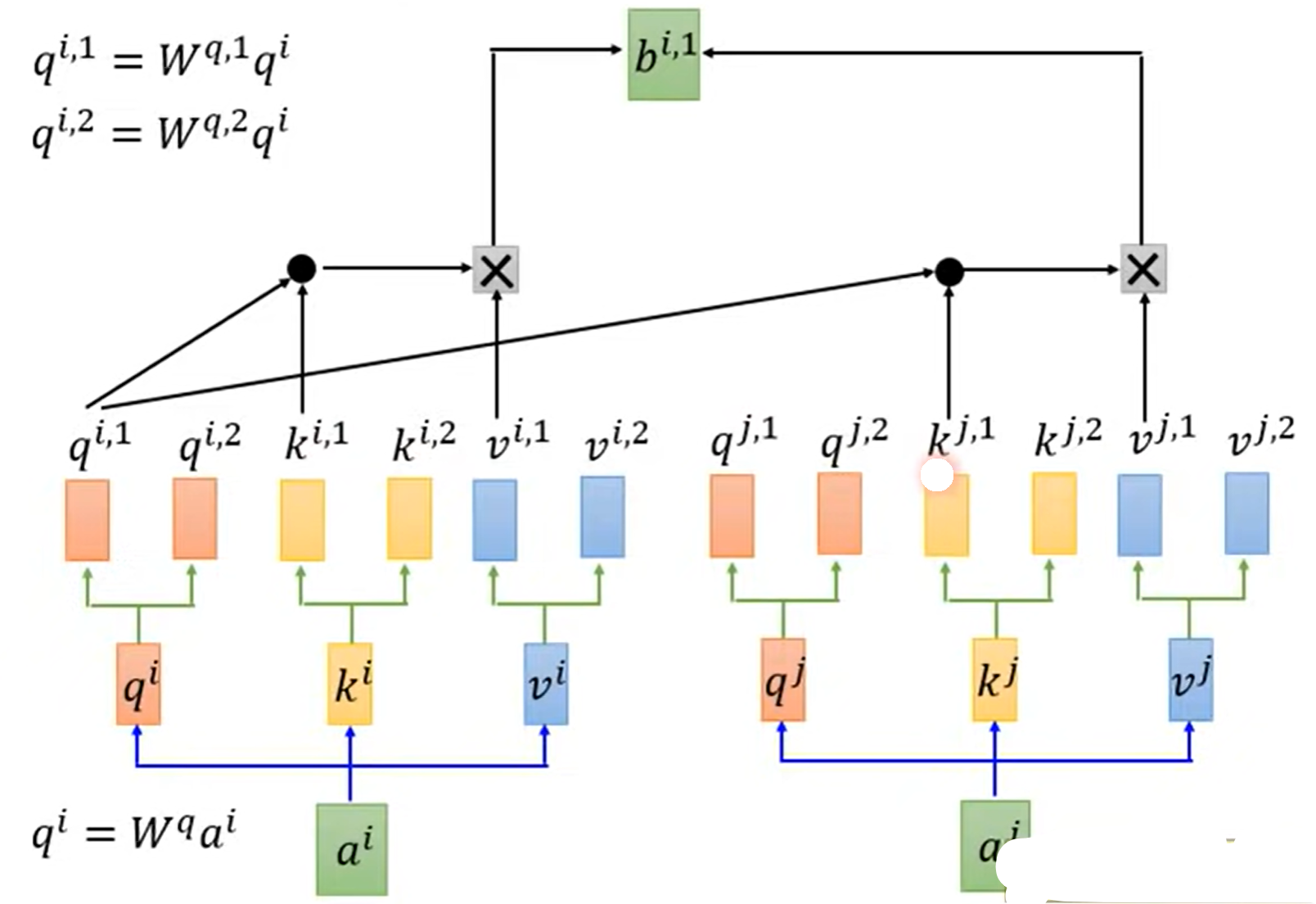
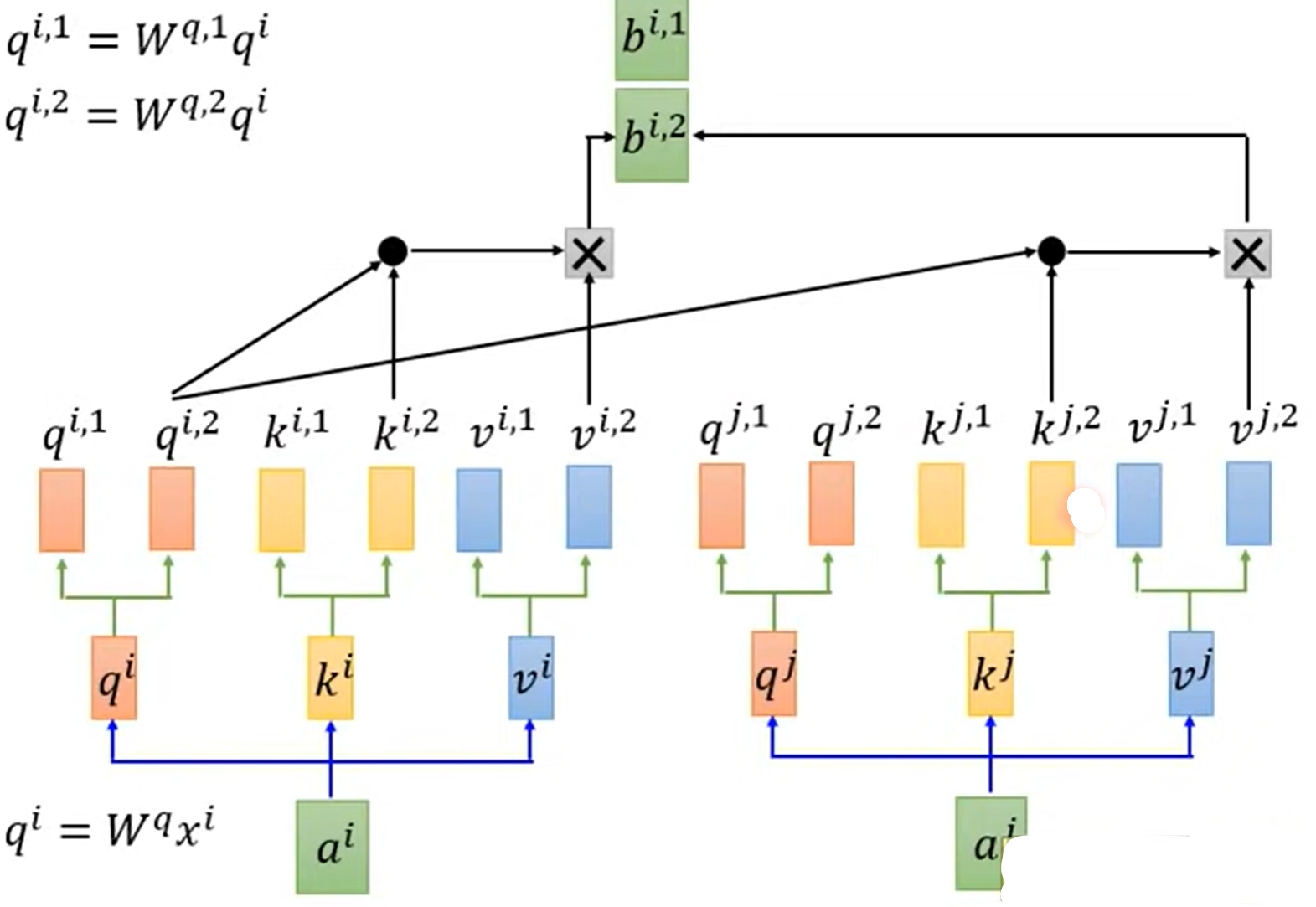
计算出$b^{i,1},b^{i,2}$后,将其按行堆叠,与矩阵$W^O$相乘达到降维目的,从而得到$b^i$: