本节主要介绍了自动编码器的基本原理及其变体,以及生成对抗网络的基本原理。
自动编码器
1.基本概念
- 自动编码器是一种无监督的神经网络模型,其目标是通过训练网络忽略信号“噪声”,从而学习数据的低纬度表示(编码)
通常分为两步:
- 学习到输入数据的隐含特征,即编码(encoder):$x\rightarrow z$
- 用隐含特征重构原始的输入数据,即解码(decoder):$z\rightarrow x$
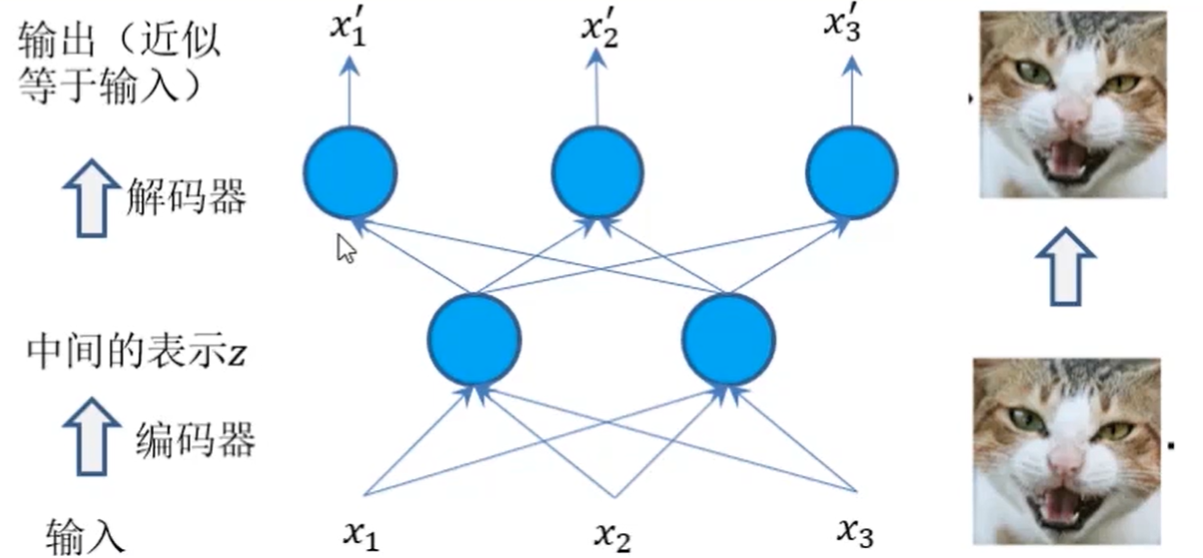
2.vanilla自编码器
在这种自编码器的最简单结构中,只有三个网络层,即只有一个隐藏层的神经网络。它的输入和输出是相同的,可通过使用Adam优化器和均方误差损失函数,来学习如何重构输入。
在这里,如果隐含层维数(64)小于输入维数(784),则称这个编码器是有损的。通过这个约束,来迫使神经网络来学习数据的压缩表征
1
2
3
4
5
6
7
8
9
10
11
12
13
14input_size = 784
hidden_size = 64
output_size = 784
x = Input(shape=(input_size,))
# Encoder
h = Dense(hidden_size, activation='relu')(x)
# Decoder
r = Dense(output_size, activation='sigmoid')(h)
autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
3.多层自编码器
如果一个隐含层还不够,显然可以将自动编码器的隐含层数目进一步提高。
在这里,实现中使用了3个隐含层,而不是只有一个。任意一个隐含层都可以作为特征表征,但是为了使网络对称,我们使用了最中间的网络层。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16input_size = 784
hidden_size = 128
code_size = 64
x = Input(shape=(input_size,))
# Encoder
hidden_1 = Dense(hidden_size, activation='relu')(x)
h = Dense(code_size, activation='relu')(hidden_1)
# Decoder
hidden_2 = Dense(hidden_size, activation='relu')(h)
r = Dense(input_size, activation='sigmoid')(hidden_2)
autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
4.卷积自编码器
使用3D矢量(如图像)而不是展平后的一维矢量。
对输入图像进行下采样,以提供较小维度的潜在表征,来迫使自编码器从压缩后的数据进行学习。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21x = Input(shape=(28, 28,1))
# Encoder
conv1_1 = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
pool1 = MaxPooling2D((2, 2), padding='same')(conv1_1)
conv1_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool1)
pool2 = MaxPooling2D((2, 2), padding='same')(conv1_2)
conv1_3 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool2)
h = MaxPooling2D((2, 2), padding='same')(conv1_3)
# Decoder
conv2_1 = Conv2D(8, (3, 3), activation='relu', padding='same')(h)
up1 = UpSampling2D((2, 2))(conv2_1)
conv2_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2, 2))(conv2_2)
conv2_3 = Conv2D(16, (3, 3), activation='relu')(up2)
up3 = UpSampling2D((2, 2))(conv2_3)
r = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up3)
autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
5.正则自编码器
除了施加一个比输入维度小的隐含层,一些其他方法也可用来约束自编码器重构,如正则自编码器。
正则自编码器不需要使用浅层的编码器和解码器以及小的编码维数来限制模型容量,而是使用损失函数来鼓励模型学习其他特性(除了将输入复制到输出)。这些特性包括稀疏表征、小导数表征、以及对噪声或输入缺失的鲁棒性。
在实际应用中,常用到两种正则自编码器,分别是稀疏自编码器和降噪自编码器。
5.1稀疏自编码器
通过对其损失函数施加约束。比如,可对损失函数添加一个正则化约束,这样能使自编码器学习到数据的稀疏表征。
在这里,隐含层中,还加入了L1正则化,作为优化阶段中损失函数的惩罚项。与vanilla自编码器相比,这样操作后的数据表征更为稀疏。
1
2
3
4
5
6
7
8
9
10
11
12
13
14input_size = 784
hidden_size = 64
output_size = 784
x = Input(shape=(input_size,))
# Encoder
h = Dense(hidden_size, activation='relu', activity_regularizer=regularizers.l1(10e-5))(x)#施加在输出上的L1正则项
# Decoder
r = Dense(output_size, activation='sigmoid')(h)
autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
5.1降噪自编码器
这里不是通过对损失函数施加惩罚项,而是通过改变损失函数的重构误差项来学习一些有用信息
向训练数据加入噪声,并使自编码器学会去除这种噪声来获得没有被噪声污染过的真实输入
因此,这就迫使编码器学习提取最重要的特征并学习输入数据中更加鲁棒的表征,这也是它的泛化能力比一般编码器强的原因
生成对抗网络(GAN)
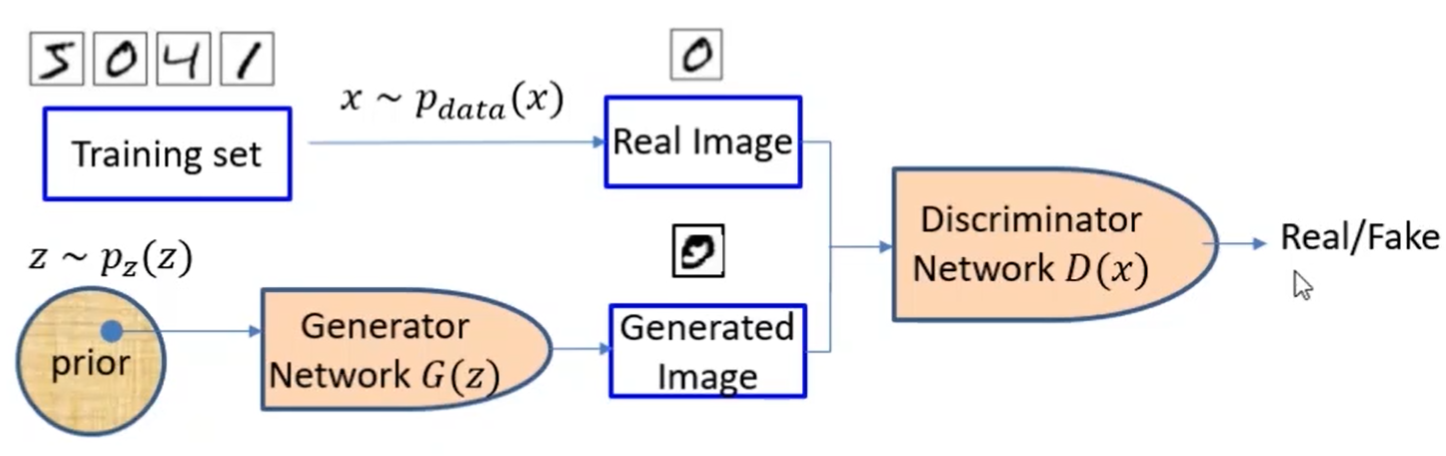
- 生成对抗网络(generative adversarial network, GAN)是通过对抗训练的方式来使得生成网络产生的样本服从真实数据分布
- 在生成对抗网络中,有 两个网络进行对抗训练。一个是判别网络,目标是尽量准确地判断一个样本是 来自于真实数据还是生成网络产生的;另一个是生成网络,目标是尽量生成判别 网络无法区分来源的样本
- 这两个目标相反的网络不断地进行交替训练,当最后收敛时,如果判别网络再也无法判断出一个样本的来源,那么也就等价于生成 网络可以生成符合真实数据分布的样本
- 生成器:从随机噪声中生成图像(随机噪声通常从均匀分布或高斯分布中获取)
- 判别器:其输入为生成器生成的图像和来自训练集中的真实图像,并对其进行判别