本节主要介绍了RNN、LSTM与BRNN
循环神经网络RNN
用于处理序列模型
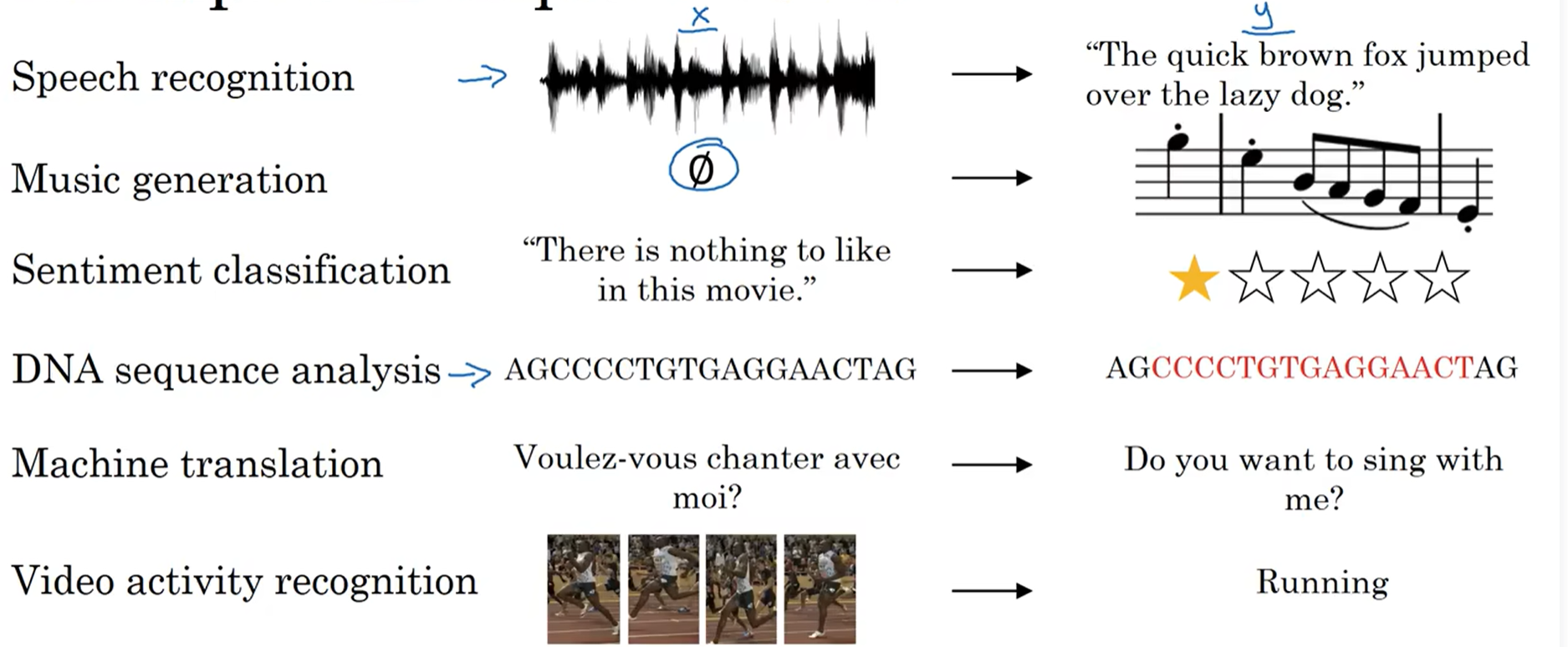
数学表示符号:

$x^{(i)
}$:表示第i个样本的第t个元素 $T_x^{(i)}$:表示第i个样本输入序列x的长度
- $y^{(i)
}$:表示第i个样本输出的第t个元素 - $T_y^{(i)}$:表示第i个样本输出序列y的长度
单词的表示:
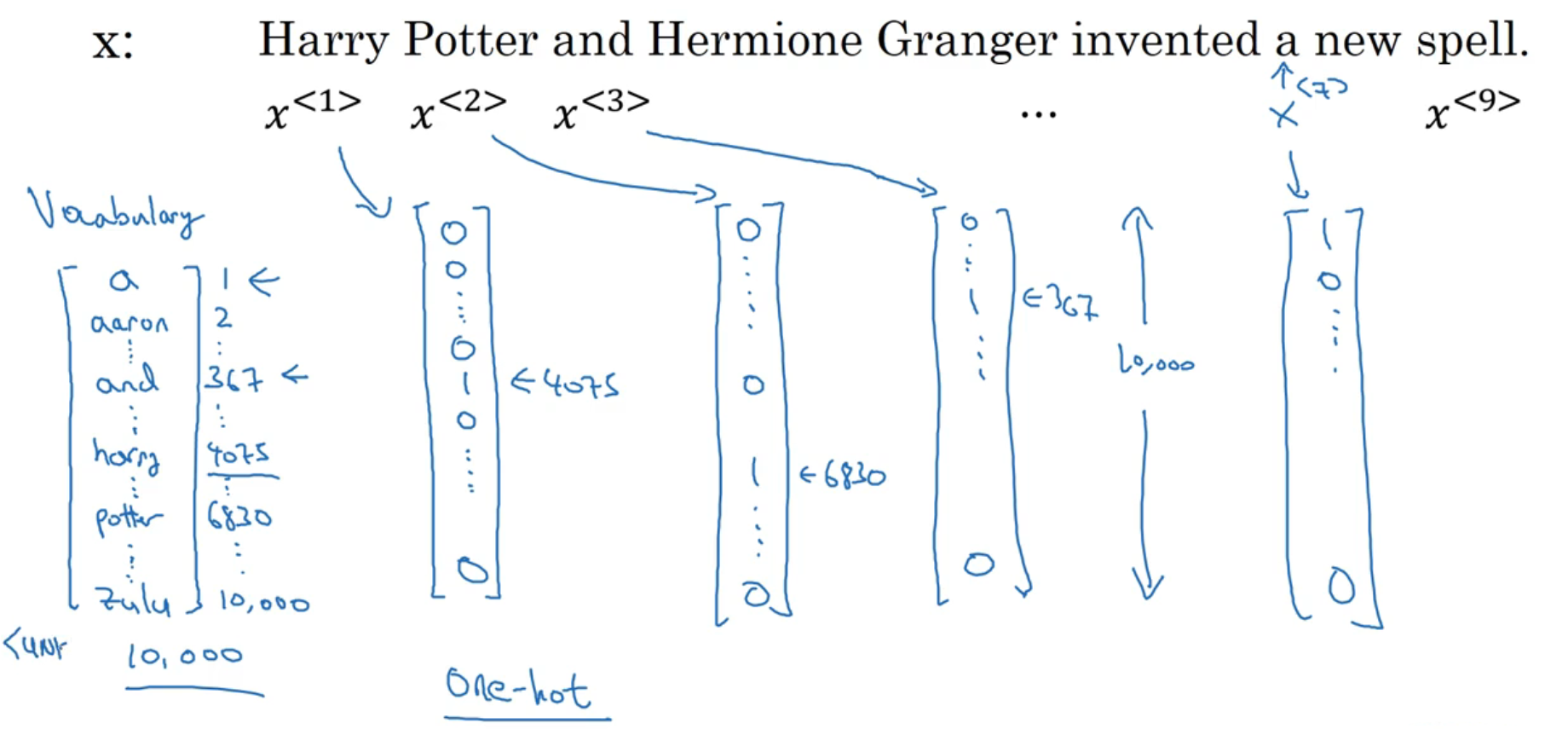
循环神经网络的结构与计算
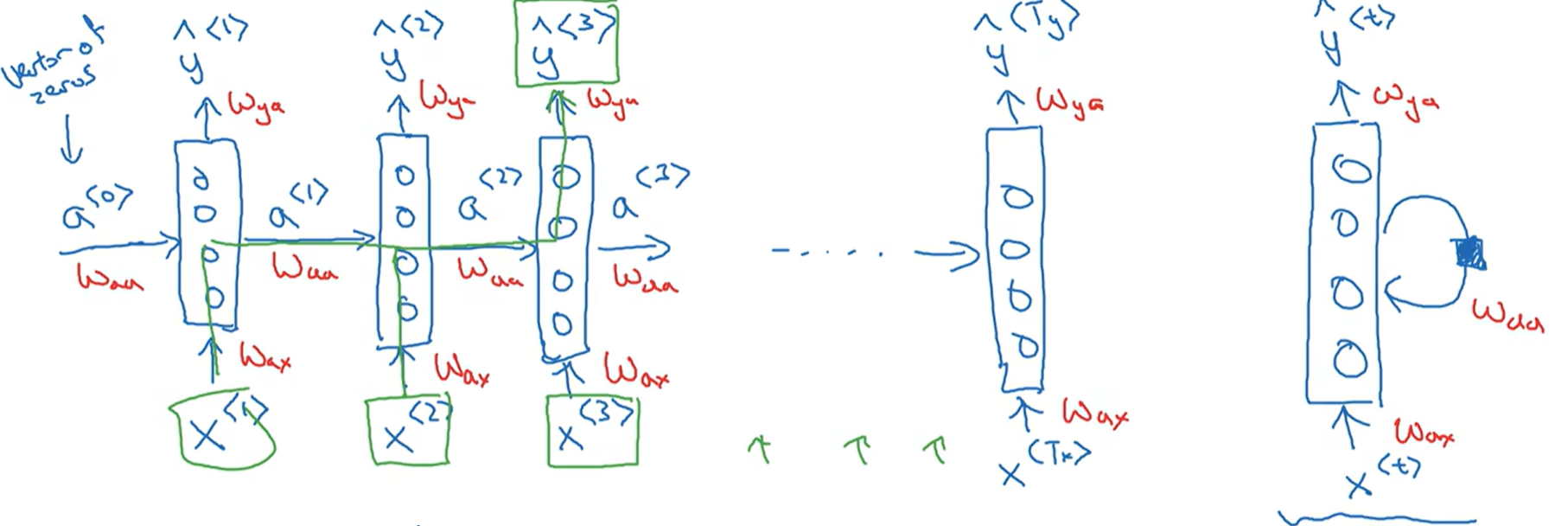
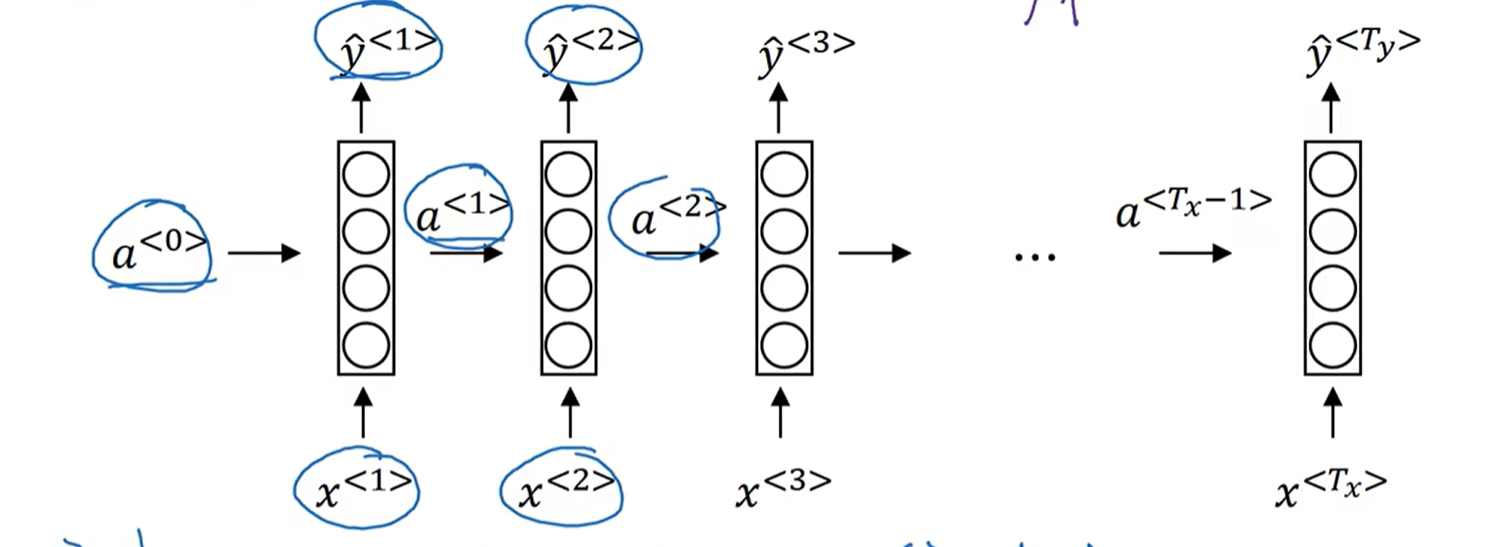
一般假设$a^{<0>}$为0的行向量,即:
$a^{<1>}、\widehat{y}^{<1>}$的计算,即:
则推导可得$a^{
}、\widehat{y}^{ }$的计公式: RNN的简化表示:
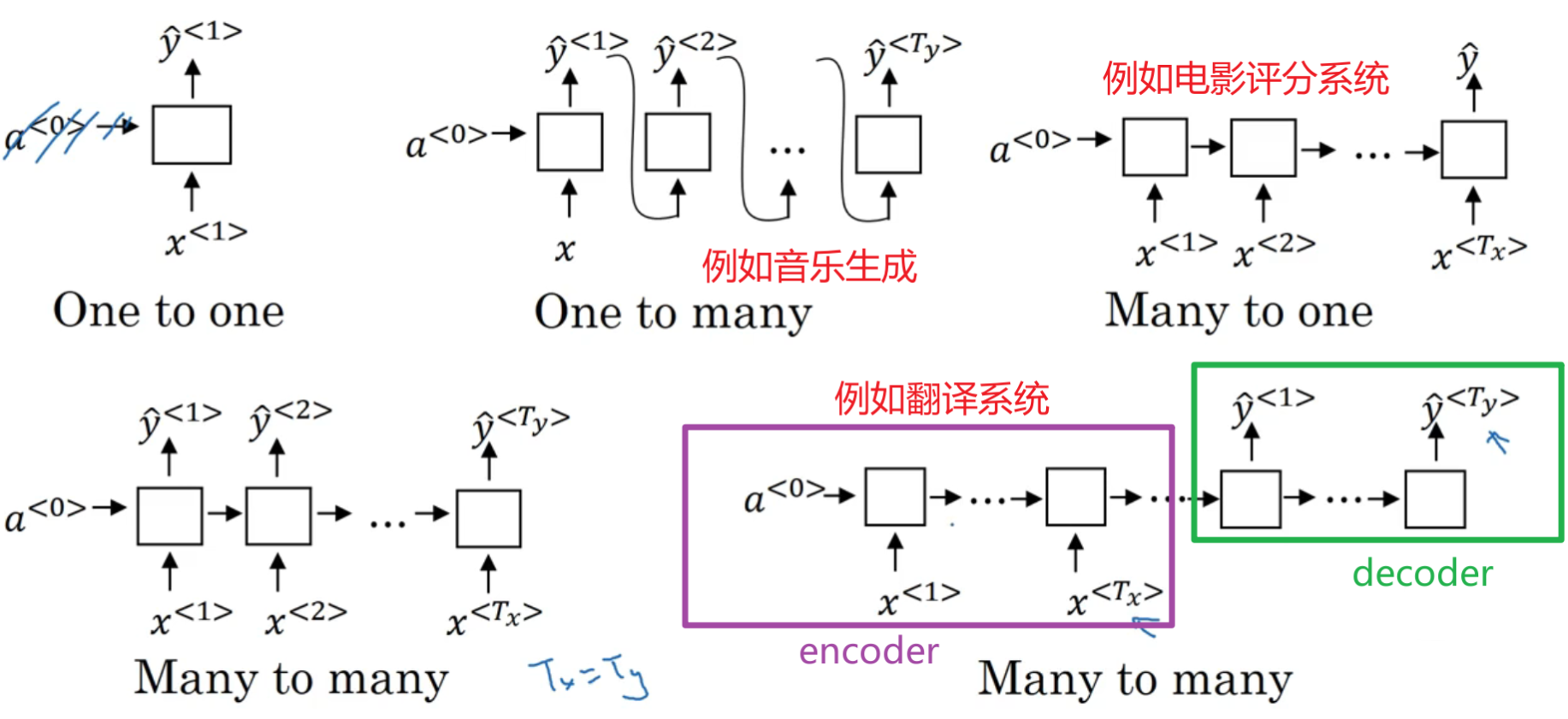
不同类型的循环神经网络:
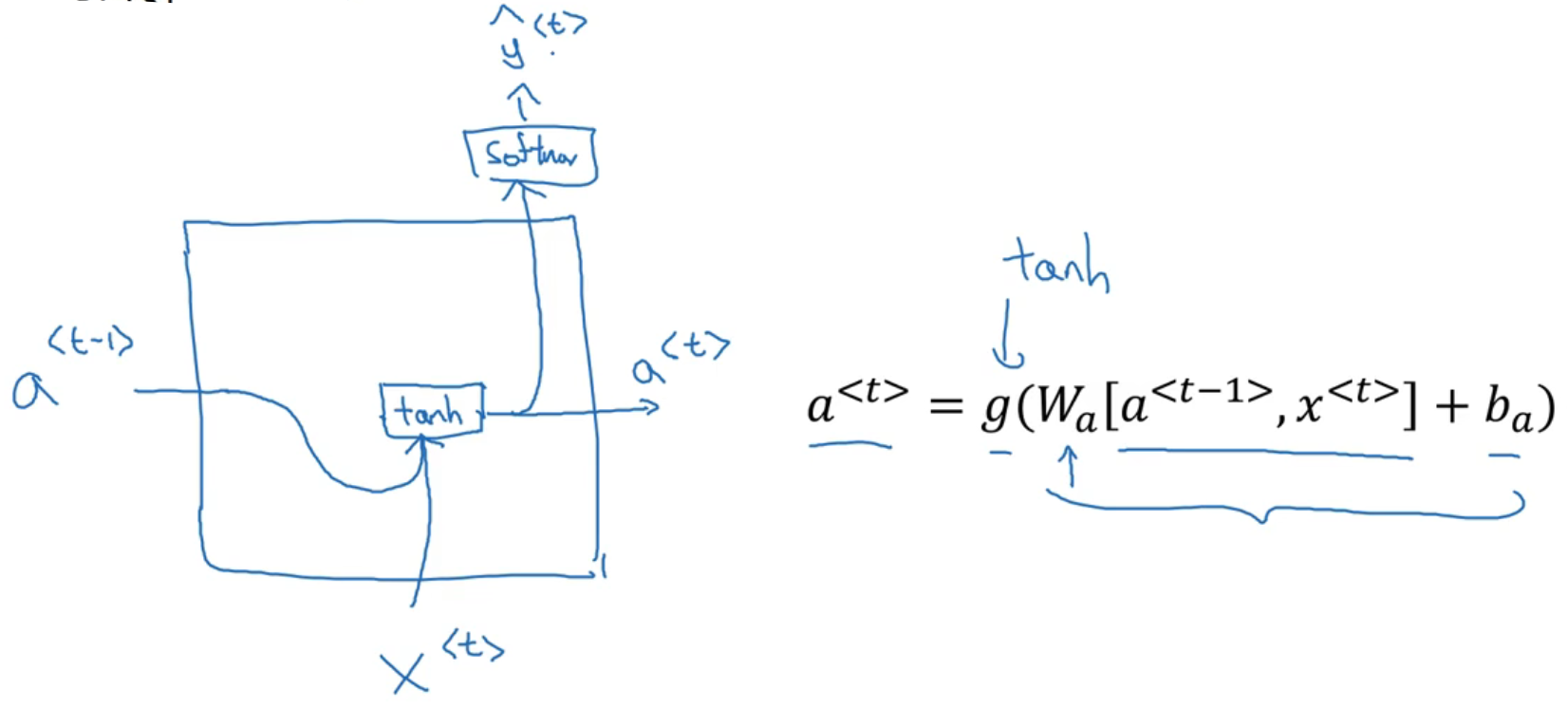
RNN单元:
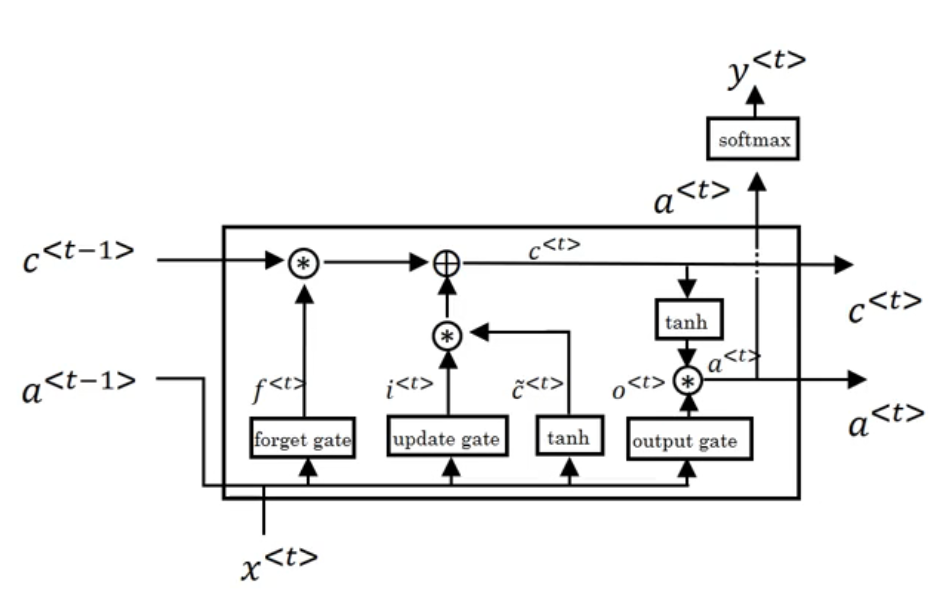
长短期记忆LSTM
- 在网络结构很深(很多层)的情况下,也能保留重要信息
- 解决了普通RNN求解过程中的梯度消失问题
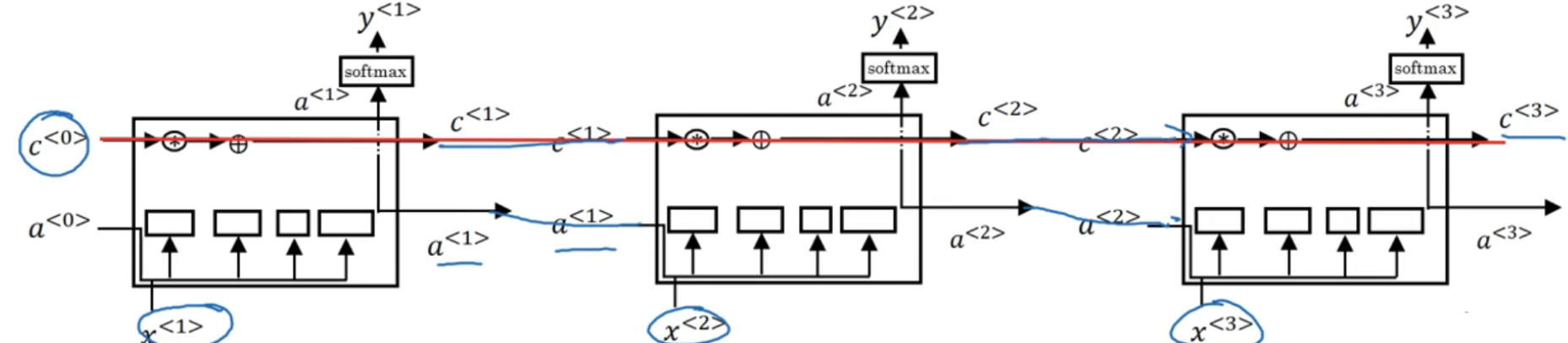
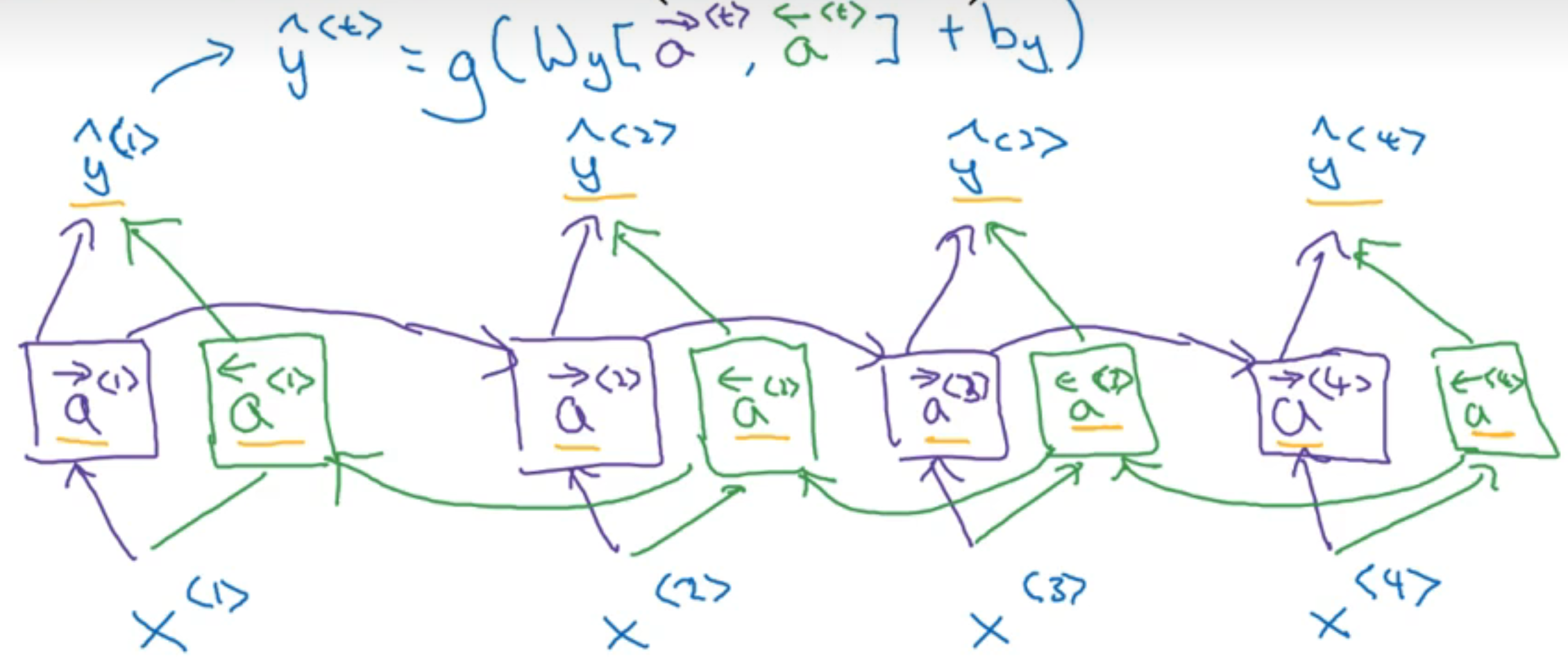
双向循环神经网络BRNN
- 做判断时,把后部序列信息也考虑