深度学习基础之信息熵与感知机

本节主要介绍了信息熵的计算与感知机算法

信息熵

• 信息熵的计算：

  $$H(U)=\sum _{i=1}^n{p}_{i}log(\frac{1}{p_i})$$

• 交叉熵：用于表征两个变量概率分布P、Q（假设P表示真实分布、Q为模型预测的分布）的差异性

  • 交叉熵越大，两个变量差异程度越大

  • 交叉熵公式：

    $$H(P,Q)=\sum _{x\in X}P(x)log\frac{1}{Q(x)}$$

• 相对熵：是交叉熵与信息熵的差值

  • 表示用分布Q模拟真实分布P，所需的额外信息

  • 计算公式：

    $$D_{KL}(P||Q)=\sum _{x\in X}P(x)log\frac{1}{Q(x)}-\sum _{x\in X}P(x)log\frac{1}{P(x)}=\sum _{x\in X}P(x)log\frac{P(x)}{Q(x)}$$

  • 性质：

    • 相对熵(KL散度)不具有对称性，即：

      $$D_{KL}(P||Q)\ne D_{KL}(Q||P)$$

    • 相对熵具有非负性

      $$D_{KL}(P||Q)\ge 0$$

• JS散度：具有对称性，现有两个分布$p1,p2$，其JS散度公式为：

  $$JS(P1||P2)=\frac{1}{2}KL(P1||\frac{P_1+P_2}{2})+\frac{1}{2}KL(P_2|\frac{P_1+P_2}{2})$$

---

感知机

• 感知机是两类分类的线性分类模型，假设输入样本的特征向量x，输出实例样本的类别y，有：

  $$\begin{gathered} y=g(w\cdot x+b) \\ g\mathrm{为}\mathrm{激}\mathrm{励}\mathrm{函}\mathrm{数} \end{gathered}$$

  

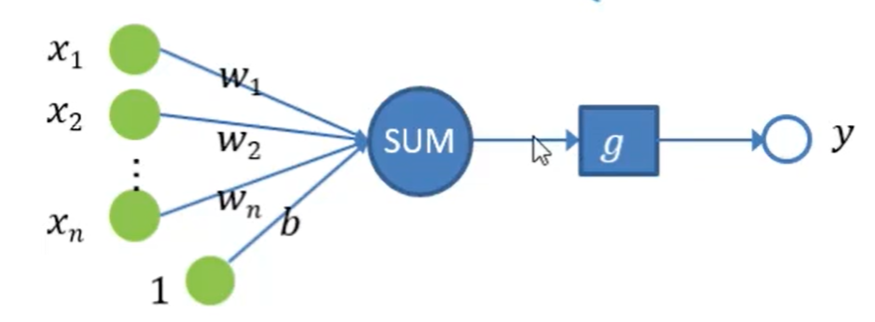
• 感知机的算法

  

• 例：