本节主要介绍了特征工程中特征处理这一核心部分,包括特征值的缩放、归一化、特征选择与降维等
特征工程的基本概念
- 定义:其本质是一项工程活动,目的是最大限度地从原始数据中提取特征以供算法和模型使用
- 特征处理是特征工程的核心部分,其包括特征缩放、特征选择及降维
- 目的:如何能够分解和聚合原始数据,以更好的表达问题的本质
特征值的缩放
1.标准化法
标准化的前提是特征值服从正态分布
标准化需要计算特征的均值和标准差,其公式为:
2.区间缩放法
区间缩放利用了边界值信息,将特征的取值区间缩放到某个特定范围,假设max和min为希望的调整后的范围,则:
由于希望的调整后范围一般为$[0,1]$,则公式变为:
特征值的归一化
归一化是依照特征矩阵的行(样本)处理数据,其目的在于样本向量在点乘运算或计算相似性时,拥有统一的标准,也就是说都转化为“单位向量”
规则为L1 norm的归一化公式如下:
规则为L2 norm的归一化公式如下:
创建多项式特征
- 如果基于线性特征的模型不够理想,也可以尝试创建多项式特征
- 例如,两个特征$(X_1,X_2)$,它的平方展开式便转化成$(1,X_1,X_2,X_1X_2,X_1^2,X_2^2)$
- 也可以自定义选择只保留特征相乘的多项式项,即将特征$(X_1,X_2)$转化成$(1,X_1,X_2,X_1X_2)$
- 得到多项式特征后,只是特征空间发生了变化
特征选择
- 单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后不改变值
1.方差选择法
- 使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征
2.皮尔森相关系数法
皮尔森相关系数显示两个随机变量之间线性关系的强度和方向,其计算公式为:
将与目标值相关性较小的特征过滤掉
- Pearson相关系数对线性关系比较敏感,如果关系是非线性的,即使两个变量具有一一对应的关系,Pearson相关性也可能接近0
3.基于森林的特征选择法
- 其原理是某些分类器,自身提供了特征的重要性分值,因此可以直接调用这些分类器,得到特征重要性分值并排序
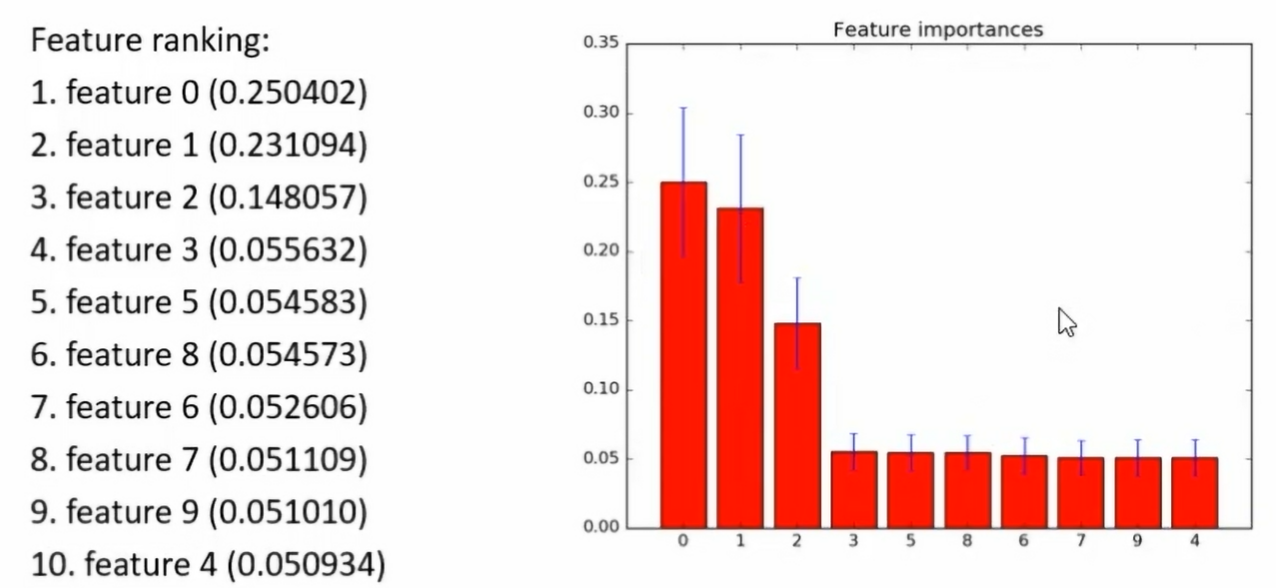
4.递归特征消除
- 首先在初始特征或权重特征集合上训练,通过学习器返回的属性来获取每个特征的重要程度
- 选择最小权重的特征移除
- 这个过程递归进行,直到希望的特征数目满足为止
特征降维
- 本质上是从一个维度空间映射到另一个维度空间,但是在映射的过程中特征值会相应的变化
1.线性判别分析法(LDA)
- 线性判别分析(LDA)是一种监督学习的降维技术,即数据集的每个样本都有类别输出
- LDA的借本思想:“投影后类内方差最小,类间方差最大”,即将数据在低维度上进行投影,投影后希望同类数据的投影点尽可能接近,而不同类数据的类别中心之间的距离尽可能的大
- 下图中,右图要更好
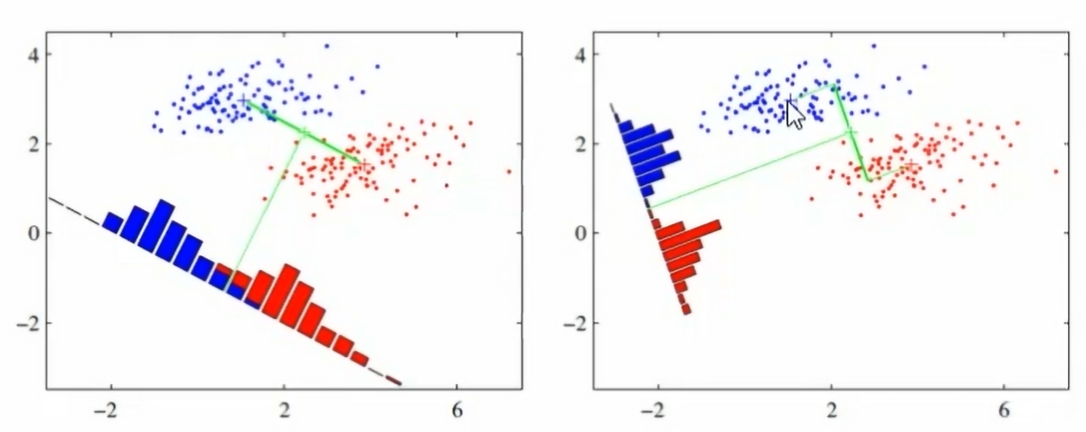
2.主成分分析(PCA)
- 主成分分析是一种无监督的降维方法
方法:寻找使方差最大的方向(数学上用方差来表达投影后分散的程度),并在该方向上投影
