本节主要介绍了数字带通调制中的高阶调制技术,以及OFDM调制与解调、CORDIC的硬件设计方法。
数字带通调制的基本概念
载波的一般表达式
波形振幅系数:
基本键控方式:
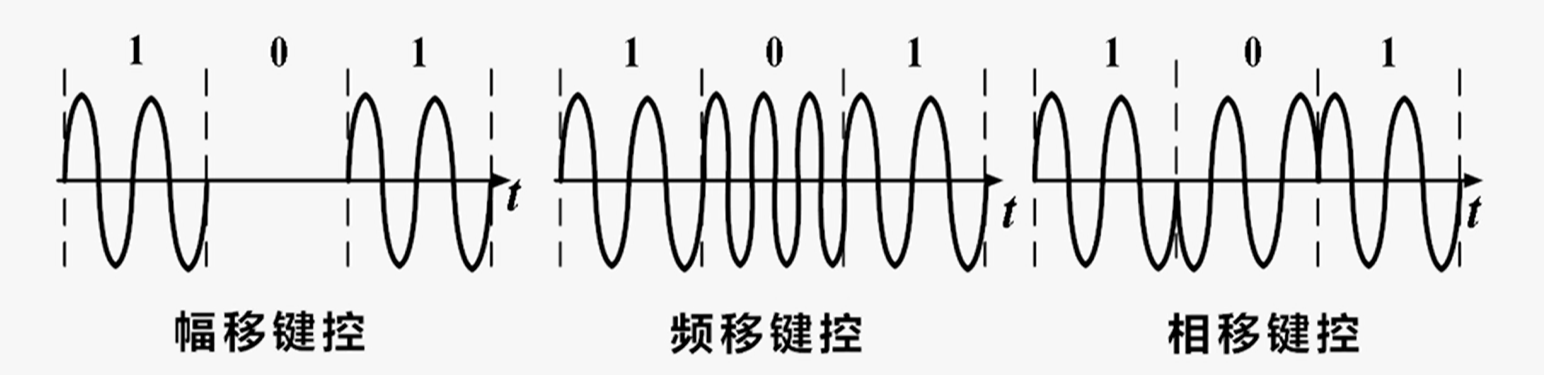
- 振幅键控(ASK):利用载波的幅度变化来传递数字信息,而其频率和初始相位保持不变
- 频移键控(FSK):利用载波的频率变化来传递数字信息
- 相移键控(PSK):利用载波的相位变化来传递数字信息,而振幅和频率保持不变
多进制数字调制
定义:在码元间隔$0\leq t\leq T_s$内,可能发送的码元有M种,M通常为2的整数幂,则称为M进制数字调制
误码率取决于信噪比$r$:
设多进制码元的进制数为M,码元能量为E,一个码元中包含信息k比特,则有:
若码元能量E平均分配给每个比特,则每比特的能量$E_b$等于$\frac Ek$:
高阶调制与解调技术
1.多进制调制
原理:
故在相同带宽内传输更多比特的信息,信道的频率效率提高至$log_2M$倍
但噪声容限会降低
- 暴露问题:随着M增加,距离减小,误码率增加
2.MQAM调制
振幅和相位联合键控的调制方式
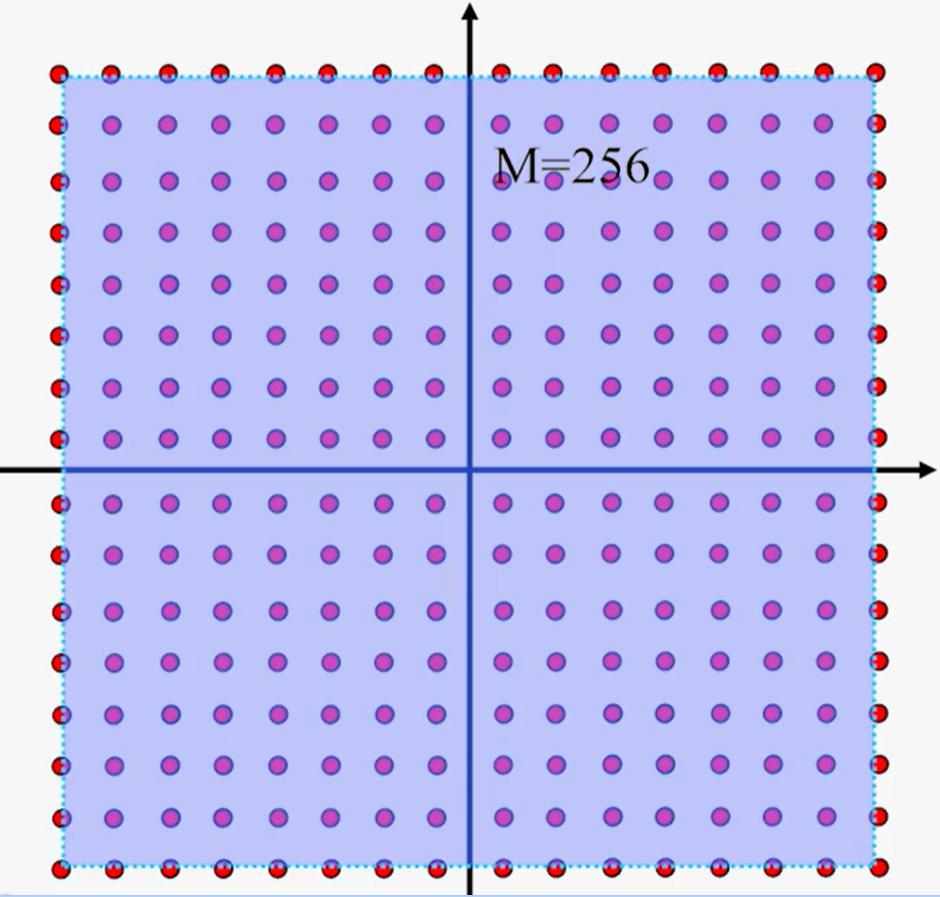
MQAM调制星座图(M=4,16,64,256)
- 随着调制阶数M增加:传输速率提升,相邻信号点距离减小,误码率提升
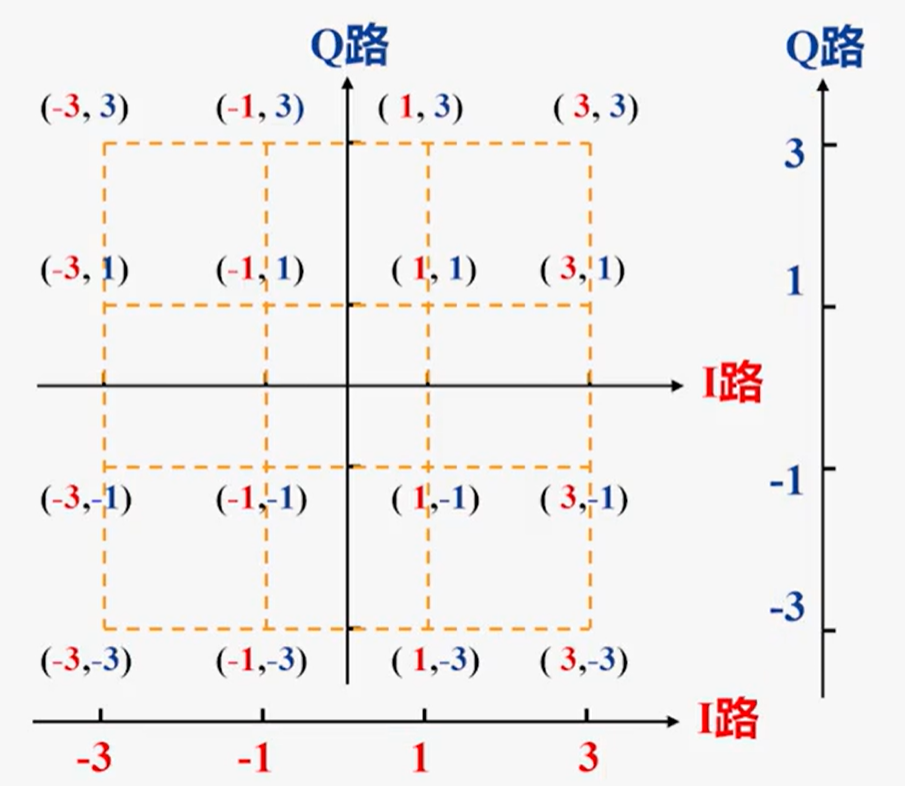
16QAM信号的产生方法:
正交调幅法:用两路独立的正交4ASK信号叠加,形成16QAM信号
复合相移法:用两路独立的QPSK信号叠加,形成16QAM信号
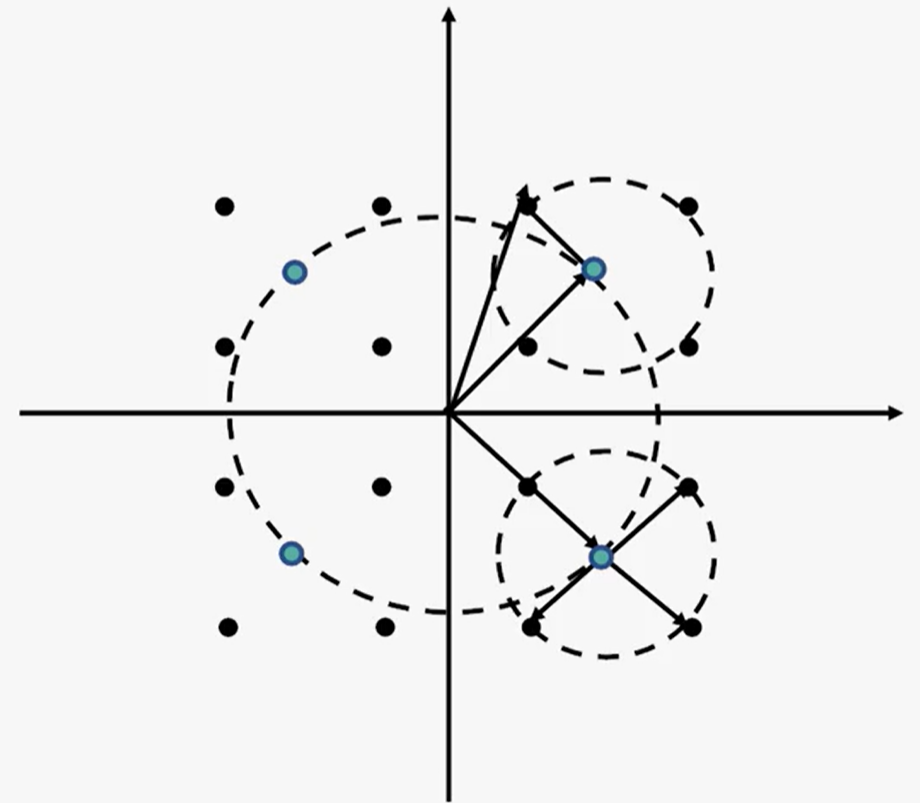
16QAM与16PSK的对比:
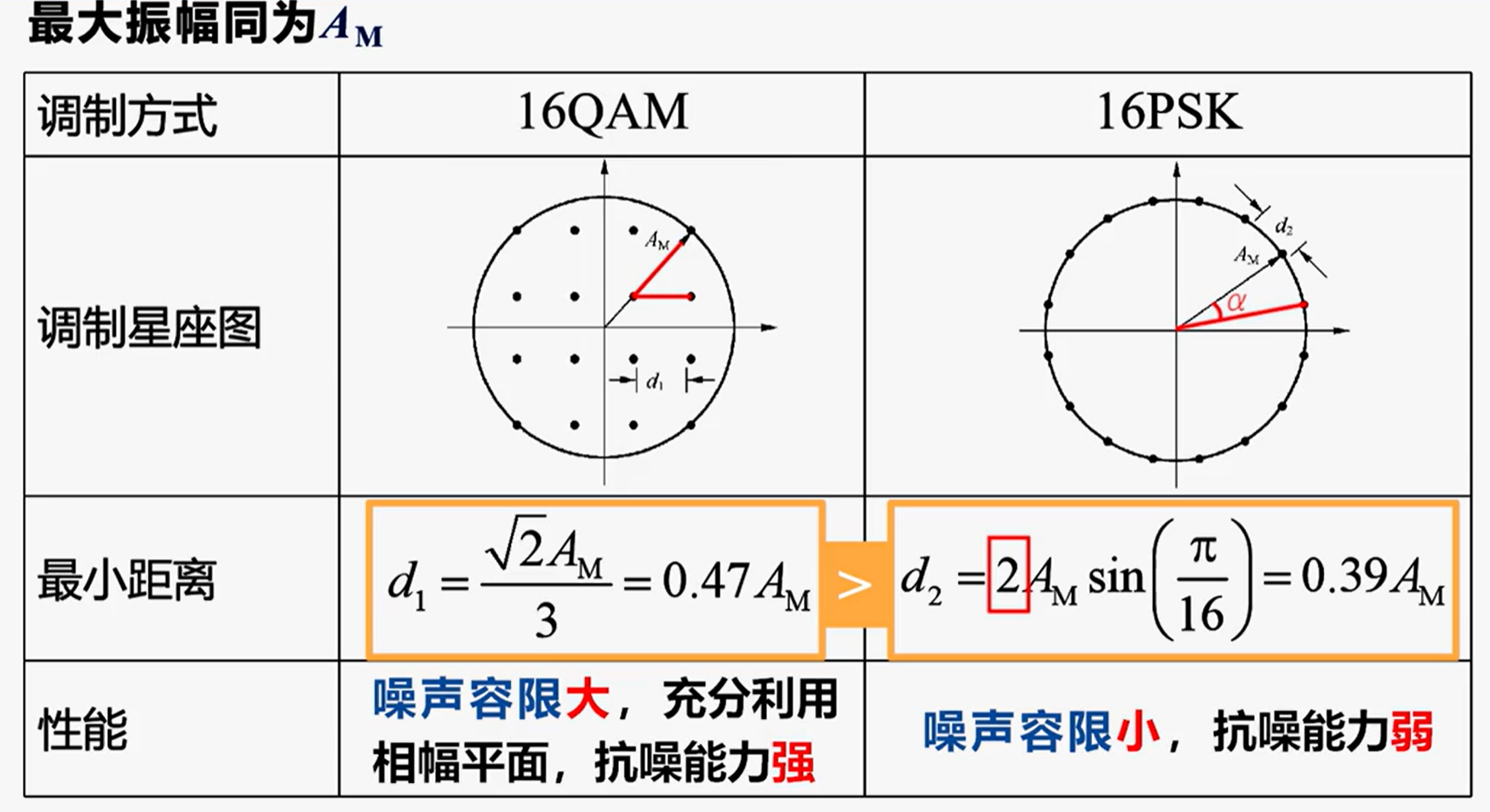
MQAM解调系统仍是一种线性系统,解调后叠加的噪声仍为高斯白噪声
同相和正交信号电平数为:
AWGN信道下的误比特率:
- MPSK与MQAM的误比特率随着M的增大而增大
- M相同时,MQAM的误比特率比MPSK小
OFDM调制与解调的原理
OFDM系统把高速数据流通过串并转换,分解成若干低速的子数据流,用多个正交子载波去调制
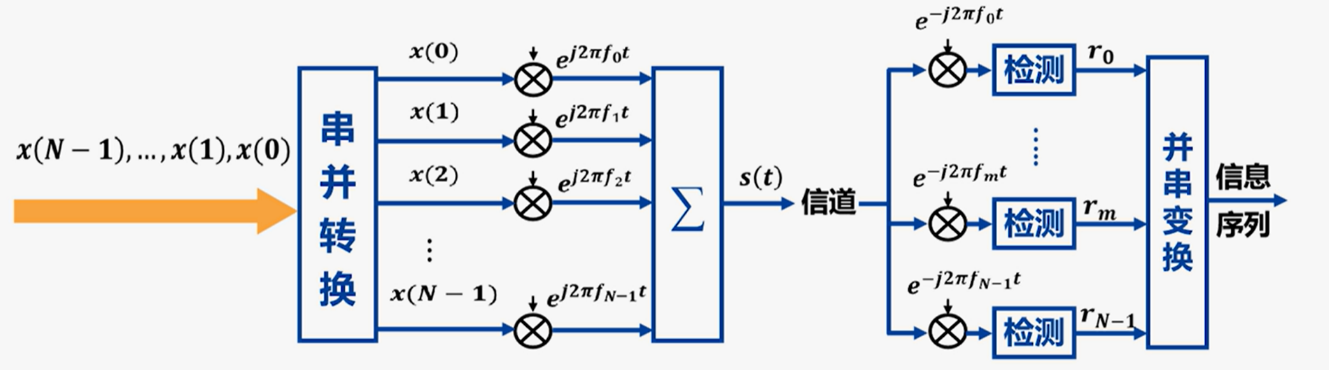
信号的正交性:对于任意两个函数$S_1(t)$和$S_2(t)$,如果有$\int_0^TS_1(t)S_2(t)dt=0$,则函数$S_1(t)$和$S_2(t)$在区间$(0,T)$上正交
对于OFDM:若相邻子载波的频率间隔$\Delta f=\frac 1T$,则子载波相互正交,有:
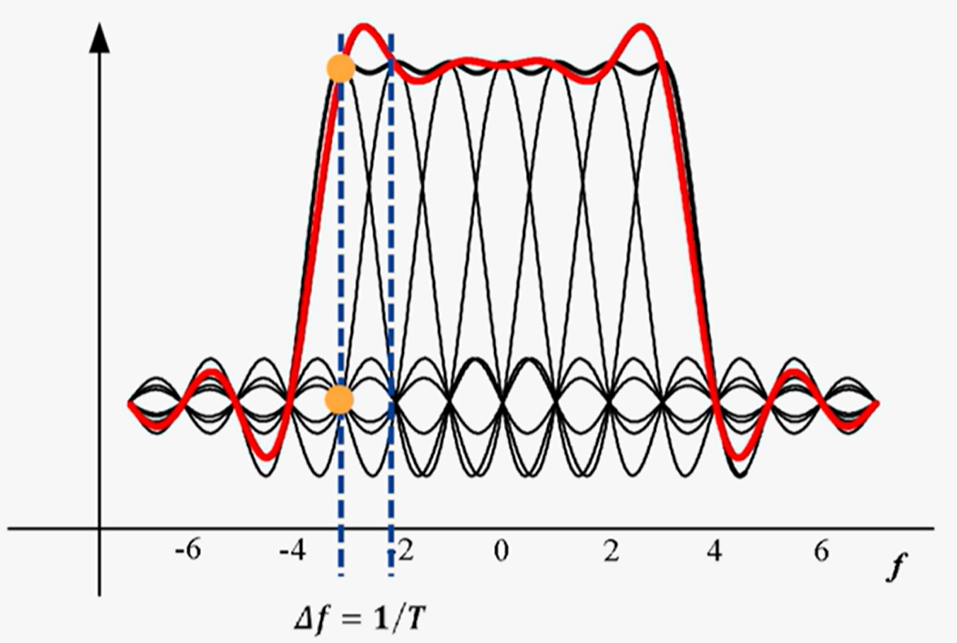
OFDM系统频谱:每个载波在其自身取最大值时,其他载波都取0,降低了带宽
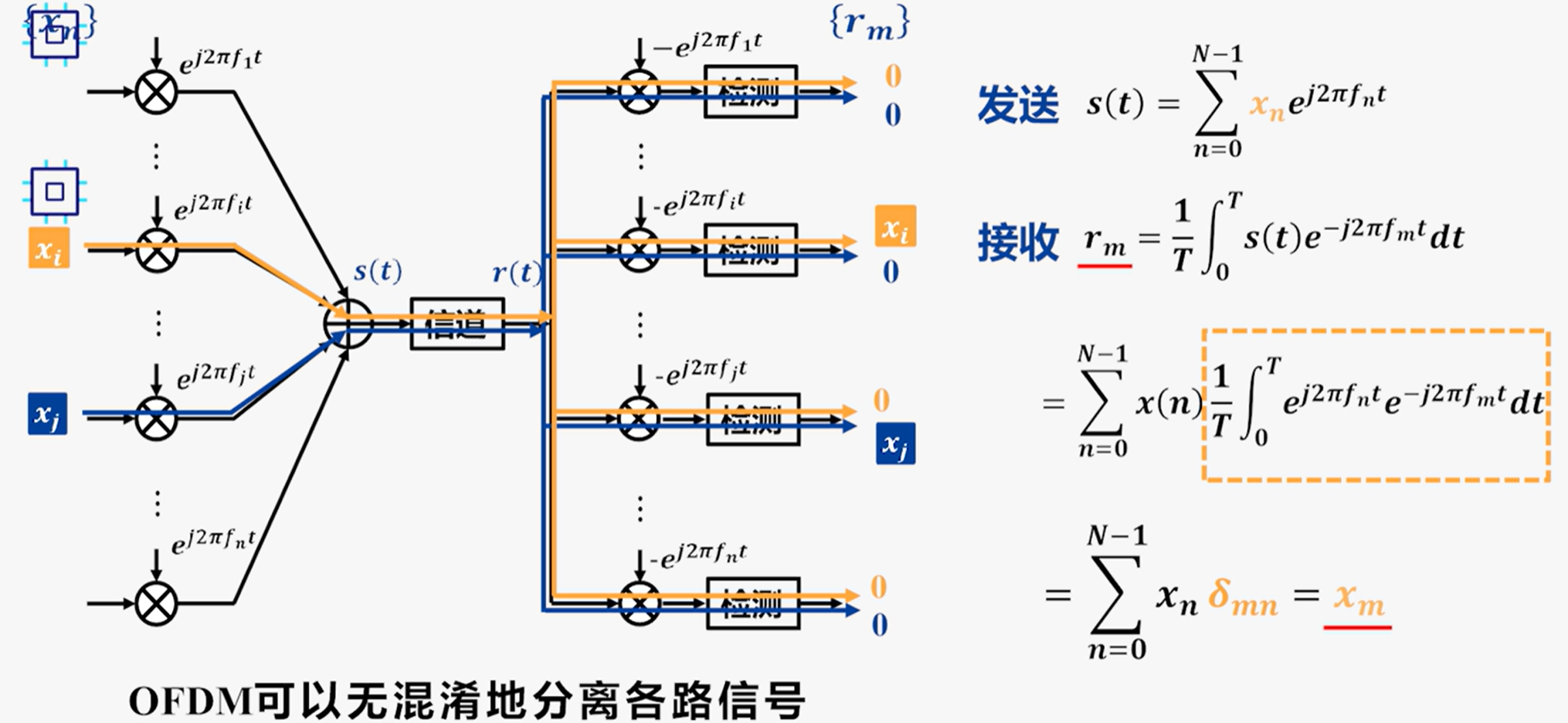
OFDM调制与解调的实现
OFDM调制通过IFFT实现,解调通过FFT实现
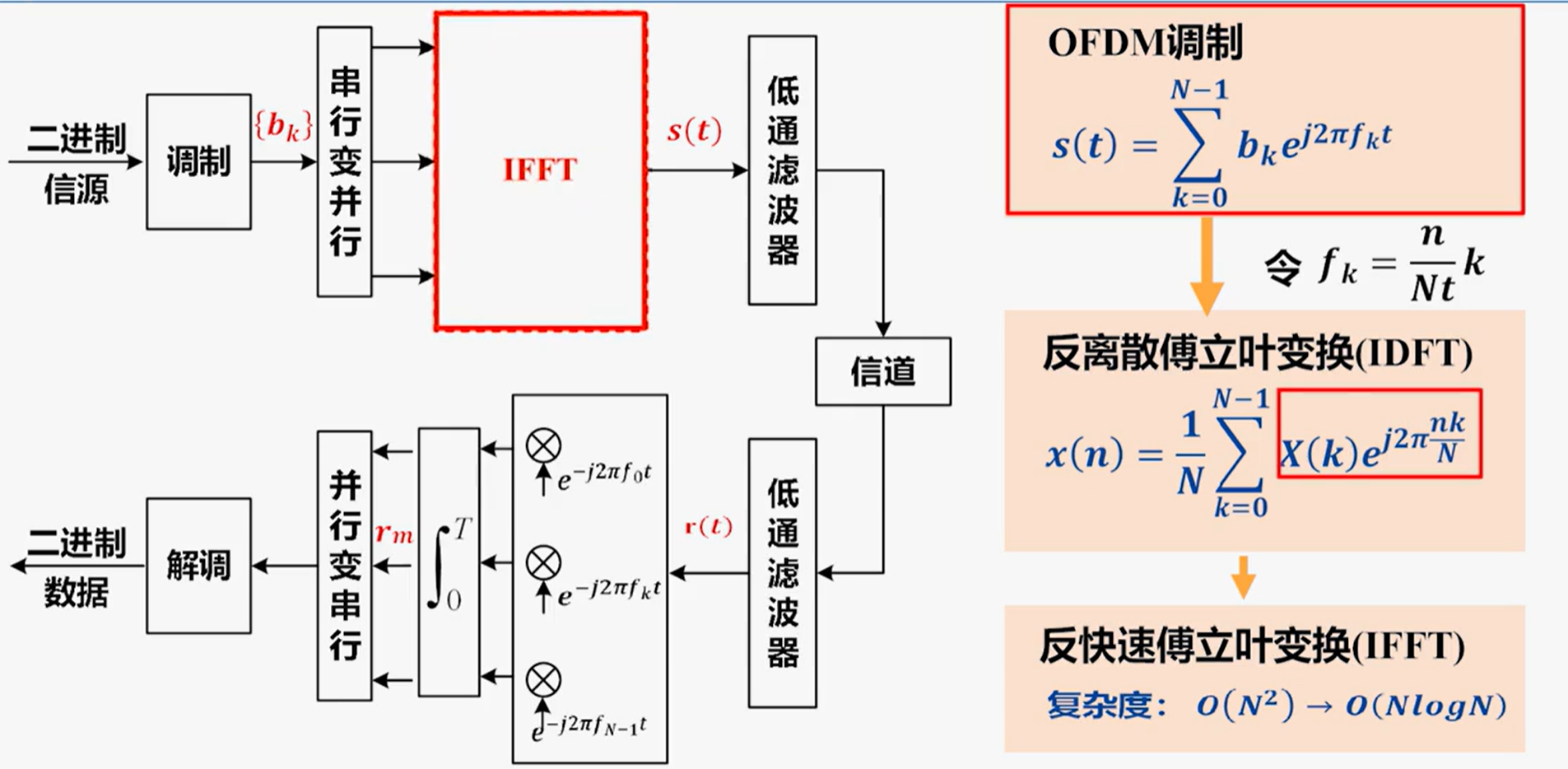
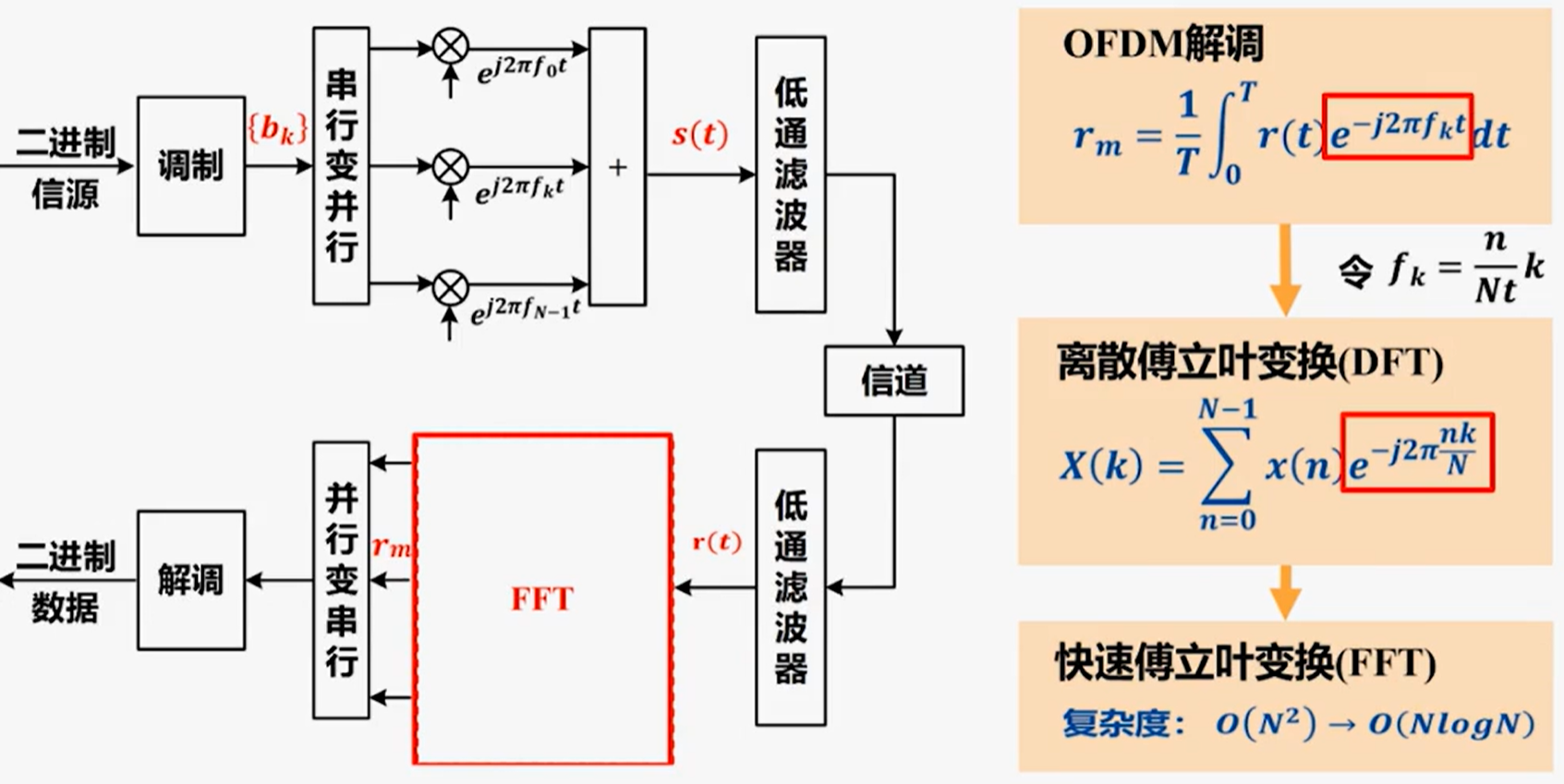
系统设计需考虑的参数:
明确系统参数:比特速率、带宽、误码率要求、根均方时延
保护时隙长度:2-4倍信道的扩展时延
符号长度:OFDM符号长度一般选择时保护时隙的5倍,以尽量减小SNR损失
子载波个数:
- 各子载波间距的大小也受到载波偏移及相位稳定度的影响
- 子载波的数量根据信道带宽、数据速率以及符号周期来确定
调制与信道编码:
- 由误码率决定
- 一个OFDM符号承载的比特数
保护时间:在OFDM系统中,保护时间的引入会引起带宽利用率的下降
符号周期:
为了减小保护时间引起的信噪比性能损失,符号周期必须大于保护时间,但符号周期的增加意味着子载波数量的增加以及系统复杂度的上升
实际系统设计时,符号周期至少时保护周期的4~5倍
调制方式:
- OFDM系统采用的调制方式应根据功率及频谱利用率的要求来确定,常用QPSK和16QAM
- 不同子信道可采用不同调制方式。性能较好的子信道应采用频谱利用率高的方式,而衰落较大的子信道应采用功率利用率较高的方式
