本节主要介绍了毫米波雷达的测距测速测角的原理,以及距离分辨率、速度分辨率、角度分辨率等。
距离测量与距离分辨率
1.测距原理
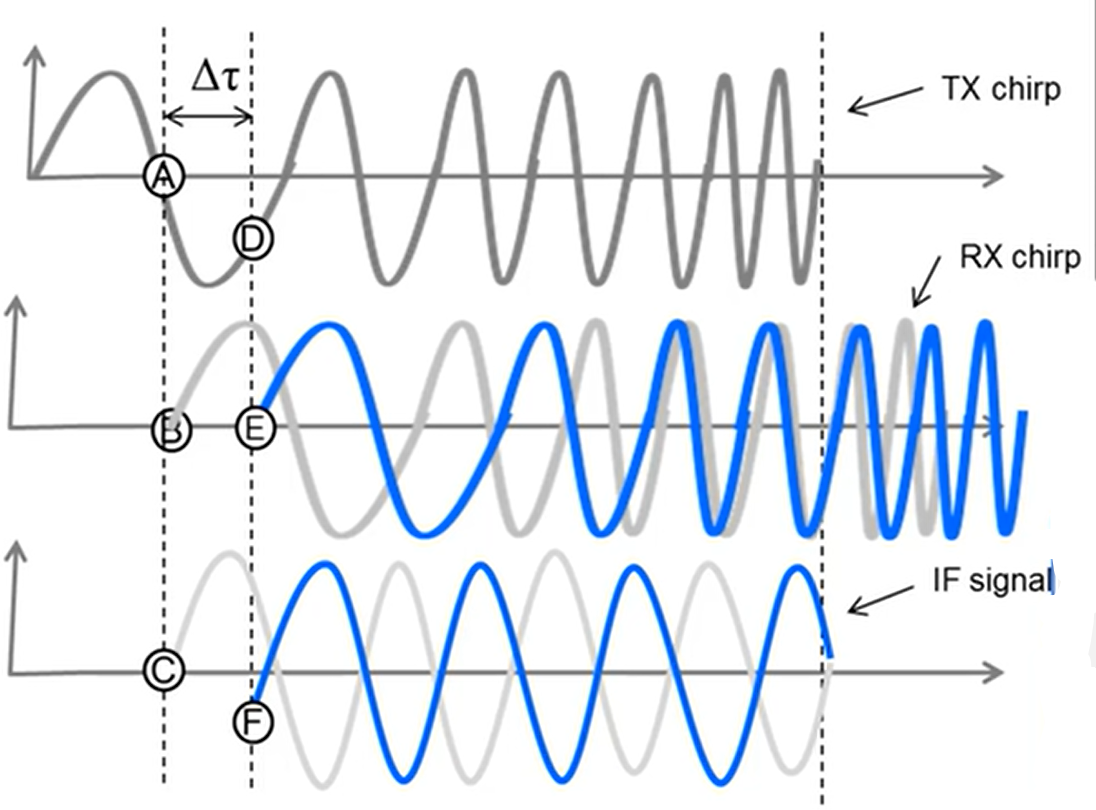
- 采用频率线性调制的连续波
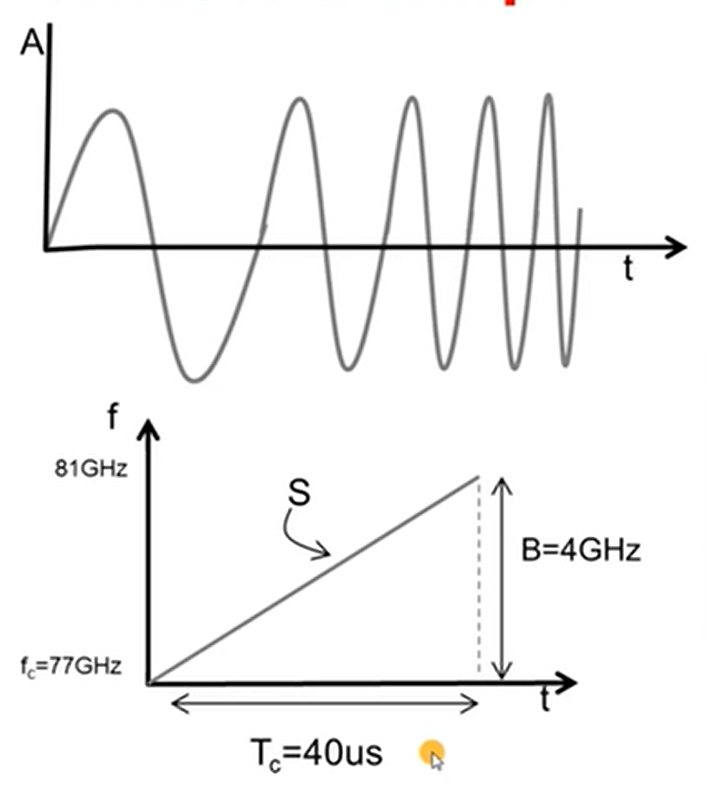
将回波信号与发射信号的差称为中频信号(IF signal)
则雷达前方的单个物体产生恒定频率的中频信号,其频率为 (根据雷达原理之目标距离测量中的三角波测距原理可推导出来):
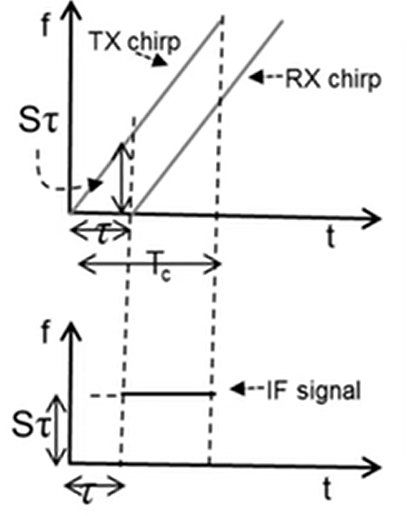
2.距离分辨率
根据傅里叶相关知识可知:观察周期越长,分辨率越高。观察周期T可以分辨出频率相差至少为$\frac1T$的信号


根据上述傅里叶知识,通过下面分析可知,想要T越长,则B需扩大,故说明B越大,距离分辨率越小
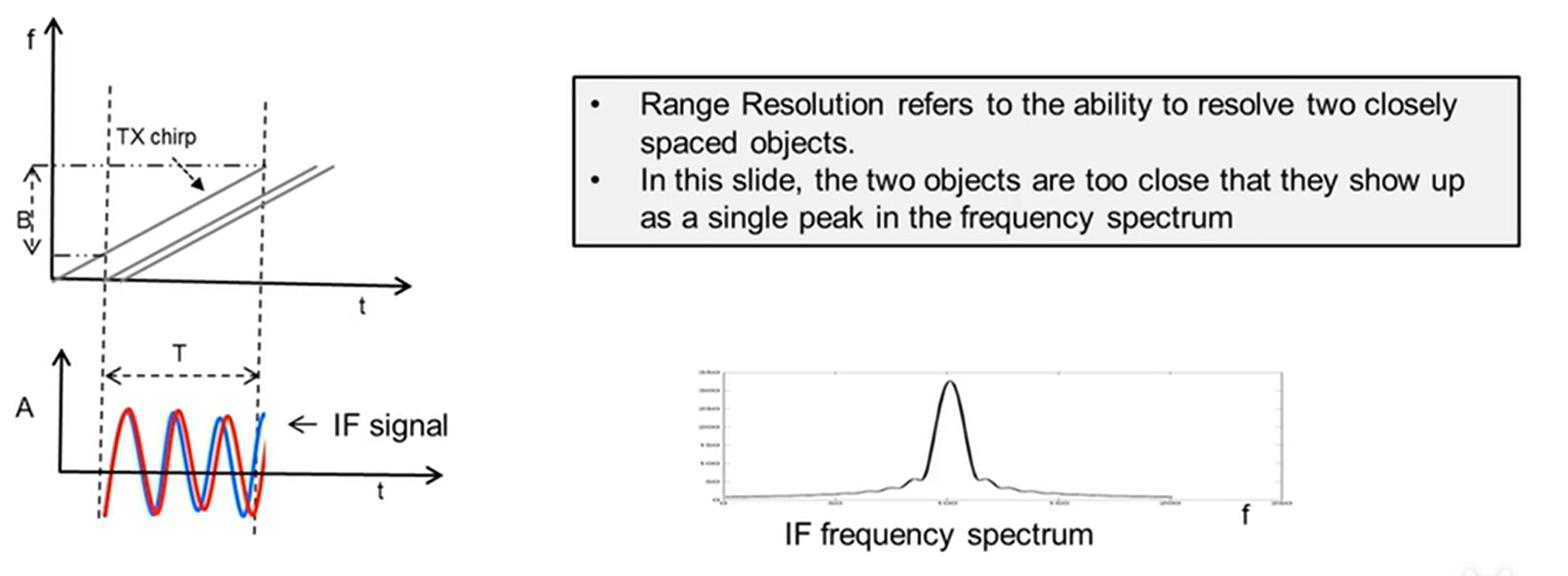

距离分辨率$d_{res}$的推导:
- 说明B越大,距离分辨率越好
3.中频信号的最大带宽
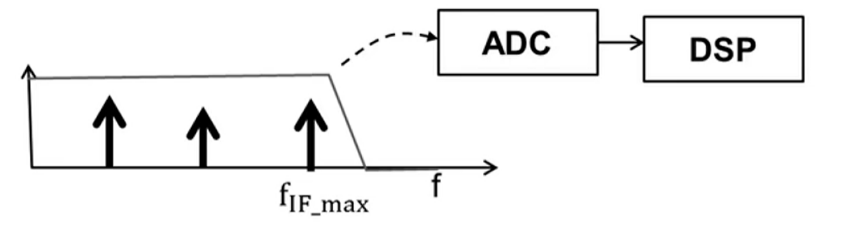
其中$f_{IF_max}$表示中频信号的最大带宽
$d_{max}$表示想要的雷达最大测距范围
故对于给定的$T_c$通常需要在最大测距范围与距离分辨率之间做取舍

速度测量与速度分辨率
1.测速原理
根据傅里叶相关知识可知:傅里叶变换后的峰值的相位就等于正弦曲线的初始相位
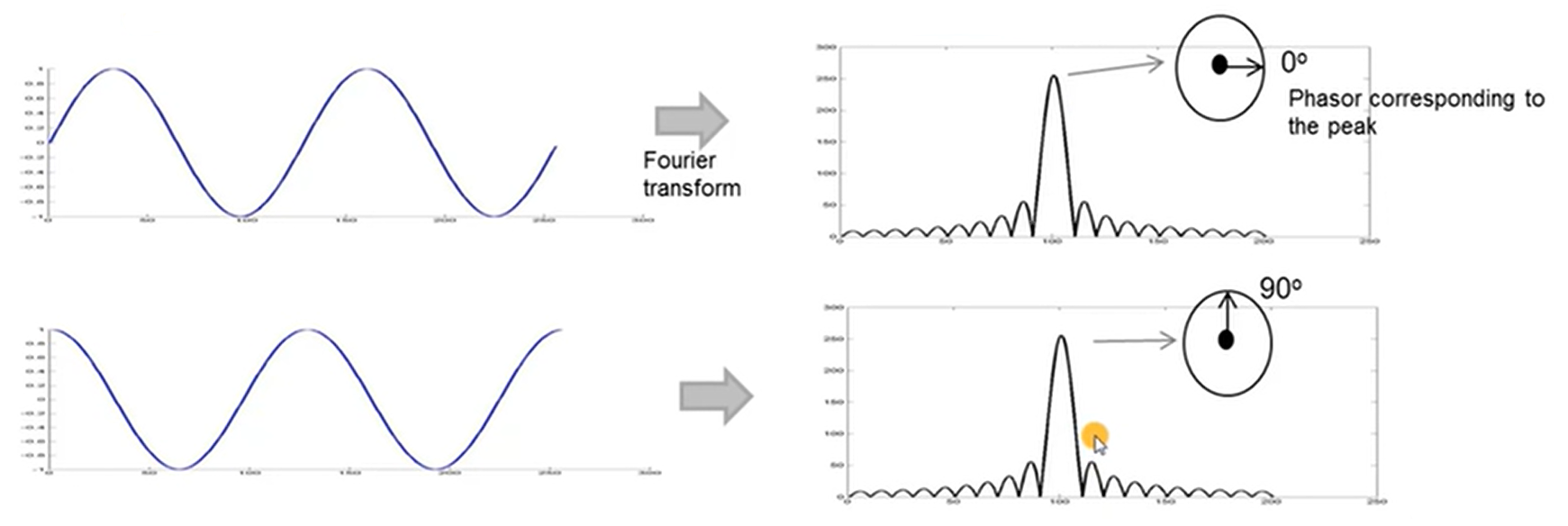
如果物体相对初始位置运动了,那么初始相位会发生变化:
变化的相位大小为:
则速度测量方法为:
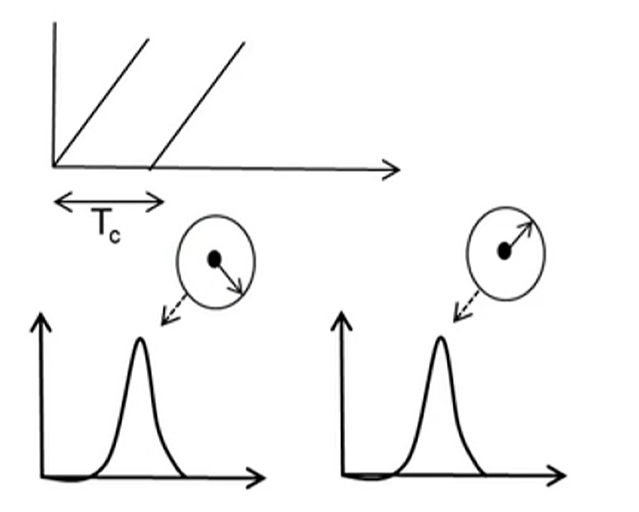
间隔时间$T_c$发送两个线性调频脉冲
其中每个线性调频脉冲对应的FFT在相同的位置具有峰值,但其具有不同的相位
设物体的运动速度为$v$,则在$T_c$时间内变化的距离为$vT_c$,故有:
$\Delta d$对频率差影响很小,却对相位差影响很大
2.最大速度
通过测量相位差进而计算速度,只有当相位差位于$-\pi \sim \pi$时才能正确测得速度,否则会产生模糊,不知道目标是远离雷达还是靠近雷达
- $w>0$:目标远离雷达
- $w<0$:目标靠近雷达

则需满足$|w|<\pi$,即:
故最大速度$v_{max}$为:
说明$T_c$越小,最大无模糊速度才越大
3.速度分辨率
若离散信号中的每个样本的相位以$w$的恒定速率旋转,那么这一系列样本点进行FFT将产生一个峰值,峰值对应于$w$

序列长度越长,分辨率就越高,序列为N的样本点,可以用来分辨旋转角频率相至少差为$\frac {2\pi}{N}$的两个相量
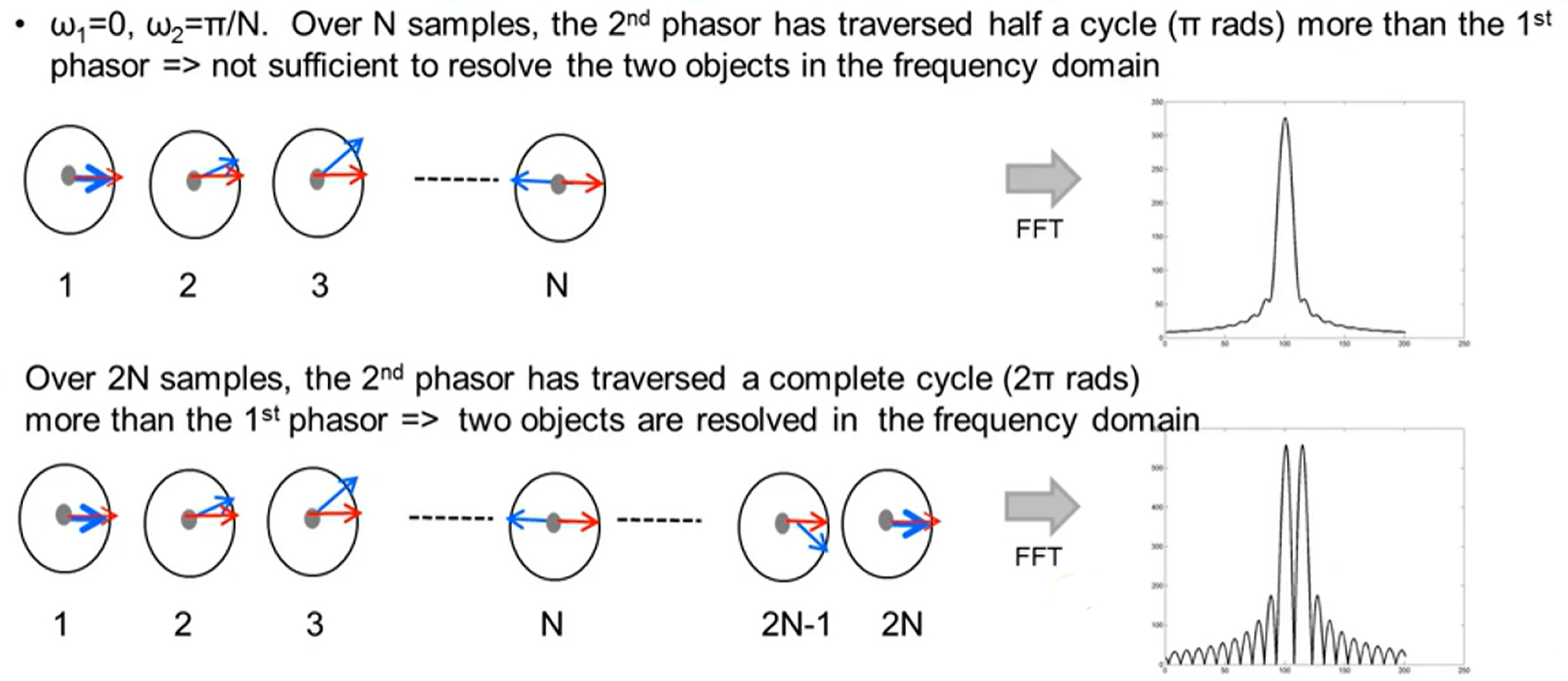
当出现多个目标时,通过发送一系列等间隔的线性调频脉冲,对得到的中频信号进行FFT获取多个目标的各自相位差
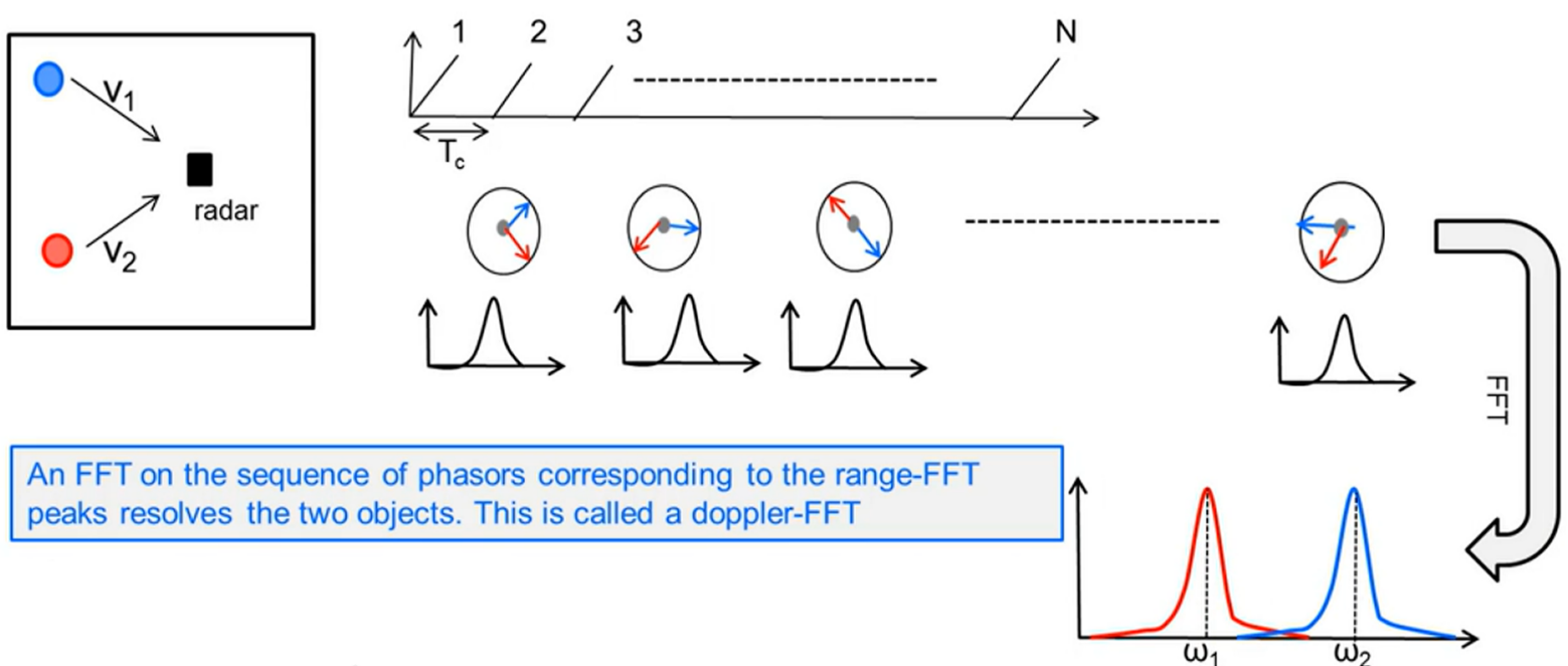
根据测速原理中的公式,有:
速度分辨率$v_{res}$的推导:
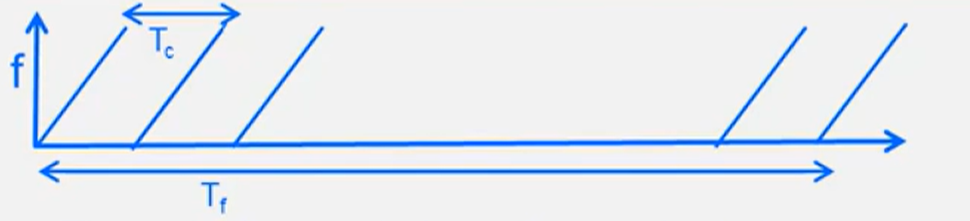
说明$T_f$越大,速度分辨率越好
角度测量与角度分辨率
1.测角原理
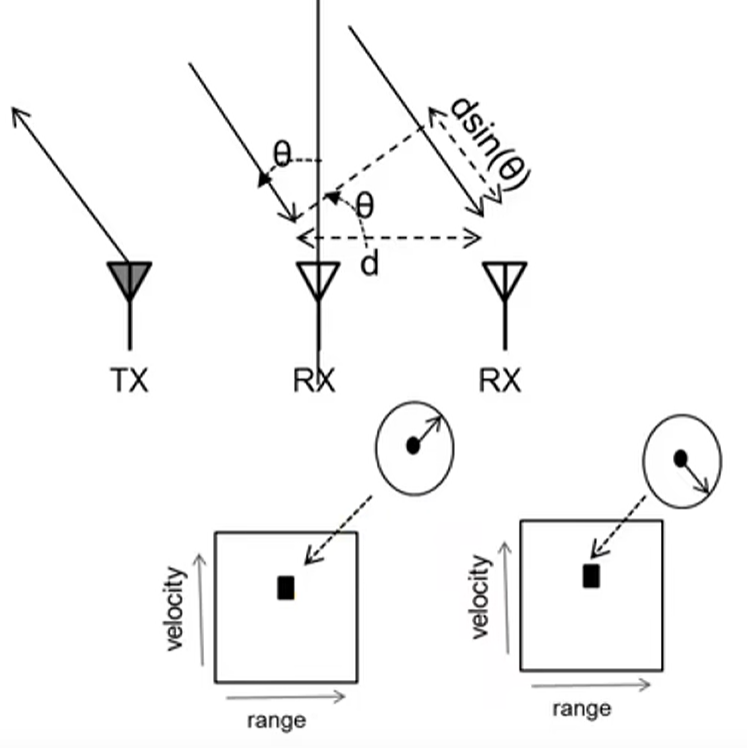
假设两天线之间的距离$d$,远远小于目标到振源的距离,则可以认为到达接收点的目标所反射的电磁波近似为平面波。
目标到$A,B$两点的距离相等,回波到$A,B$两点的相位也相等,回波到接收点的距离相差$dsin(θ)$,对应相位相差$\phi$,有:
则测量相位差$\phi$就能测量角度了
2.最大角度
当$ϕ∈[−π,π]$时,$θ$取值无模糊。$θ$对应的取值范围$[−θ_{max},θ_{max}]$

则最大测角范围,由$\phi=\frac{2\pi dsin\theta}{\lambda}$可得:
从上式可知,只要$d$越小,对应的$θ_{max}$就越大。则短基线保证大的无模糊测角范围。
3.角度分辨率
- 当出现多个目标时,通过一系列等间隔为d的接收机接收信号,对得到的中频信号进行FFT变化获取多个目标的雷达接收机之间各自相位差
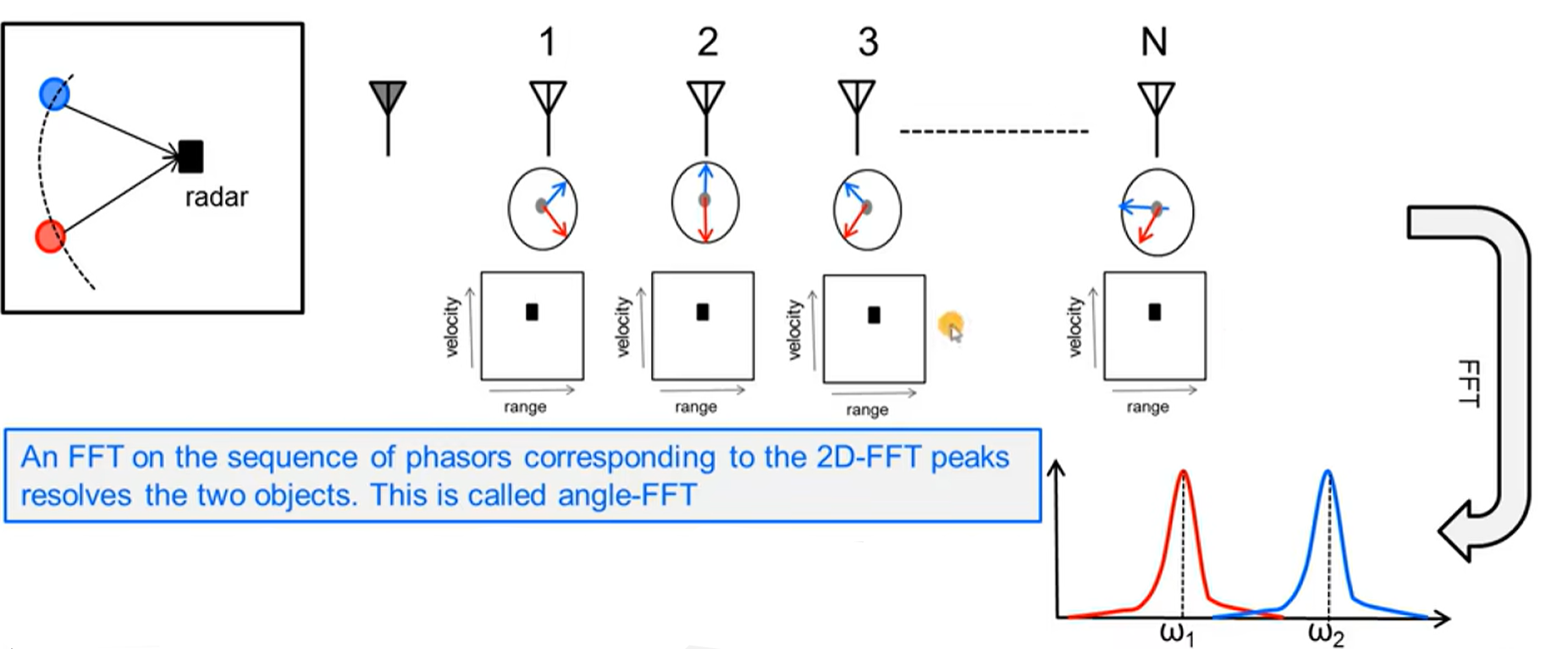
角度分辨率$\theta_{res}$的推导:
说明$Nd$越大,角度分辨率越好
