本节主要介绍了VLSI DSP中的迭代边界相关知识，包括DSP算法的四种表示方法、迭代边界的基本概念以及用LPM求解迭代边界。
关键路径
路径：数据在任意两个节点间经有向边和中间节点的通路
关键路径：没有延时单元的最长路径（DFG中在不包含延迟单元的路径中执行计算时间最长的路径$T_c$）
关键路径确定了最小可行的时钟周期
时钟速度被关键路径限制
$$
T_{clk}\ge T_{critical}
$$以4阶FIR为例：红色与紫色所示为关键路径，均包含1个乘法器和3个加法器
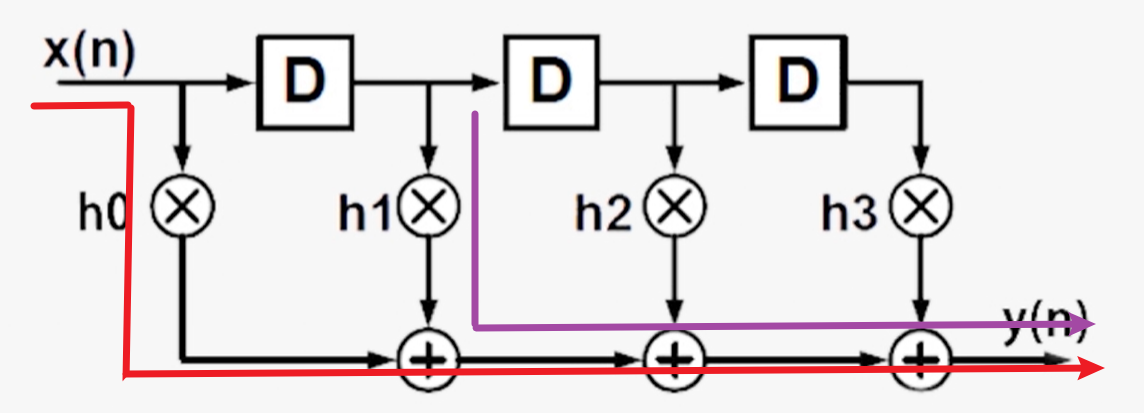
将其推广到N阶FIR，则：
$$
T_{critical}=T_M+(N-1)T_A
$$$$
其中,N为抽头系数
$$
DSP算法的表示方法
1.框图
- 常用于图形化地描述DSP系统，由功能块和有向边组成
- 有向边：表示从输入到输出的数据流动
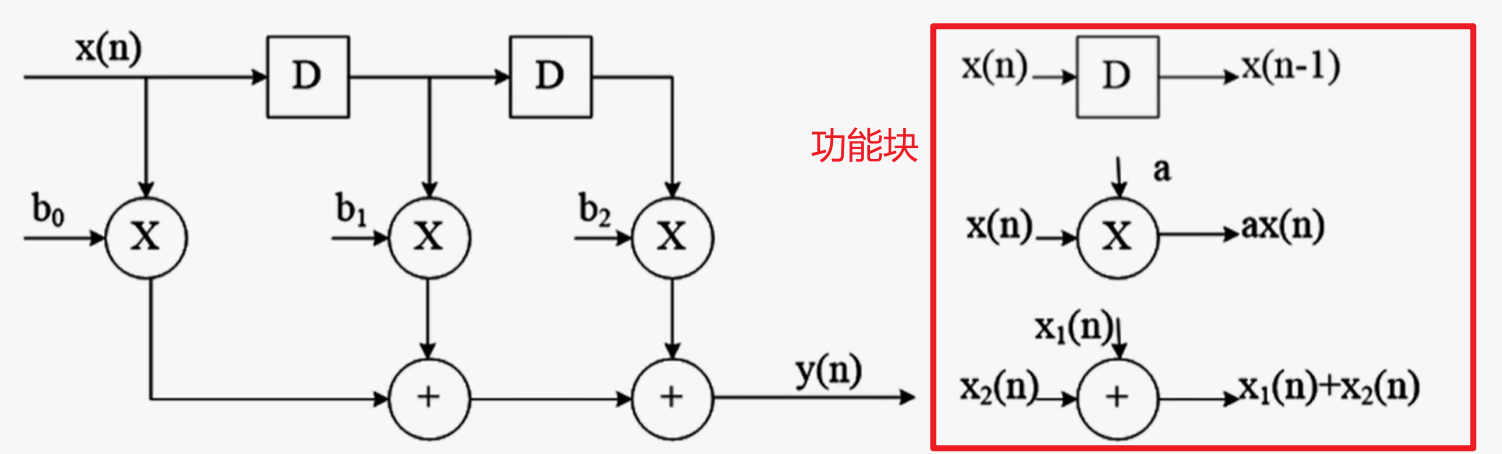
2.信号流图（SFG）
- 信号流图是一组节点和有向边的集合
- 用于分析、表示、评估线性数字网络结构
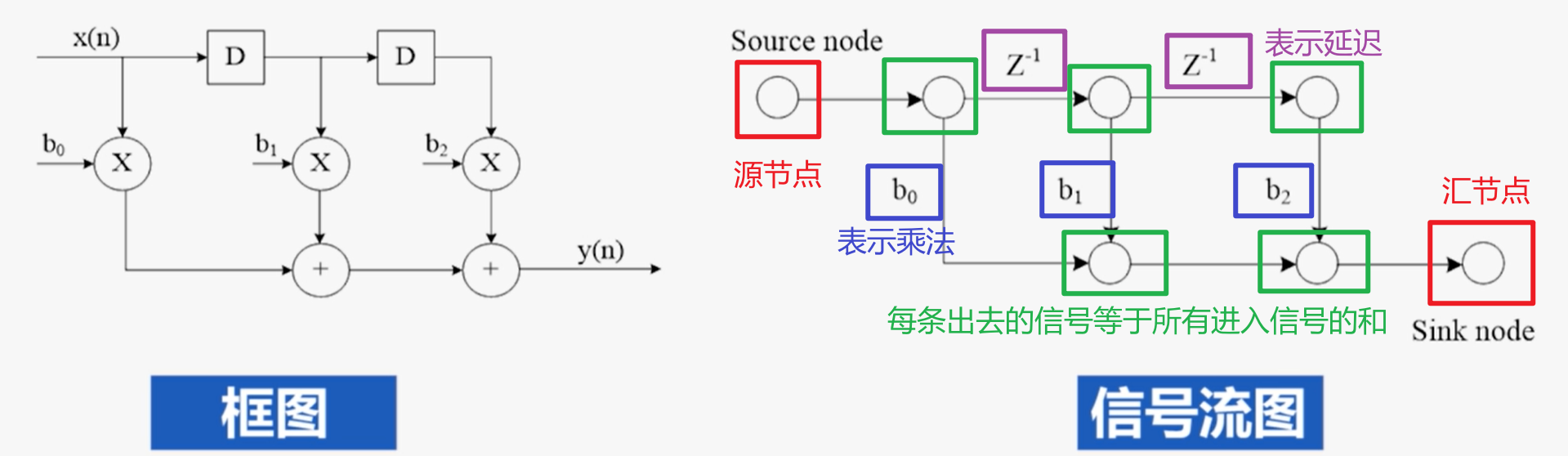
3.数据流图（DFG）
节点：
- 表示算法中计算（或功能）执行
- 包含关联的计算时间：（数字）
- 细粒度：节点简单的基本运算单元，如乘、加等
- 粗粒度：节点为子任务以上层次的复杂功能块，如滤波、FFT等
有向边：
- 包含节点间通信关系
- 包含关联的非负延迟$z^{-1}$或D
- 每条边描述了两节点间执行的优先顺序约束
- 边无延迟：描述迭代内优先顺序约束
- 边有延迟：描述迭代间优先顺序约束
同步DFG表示：
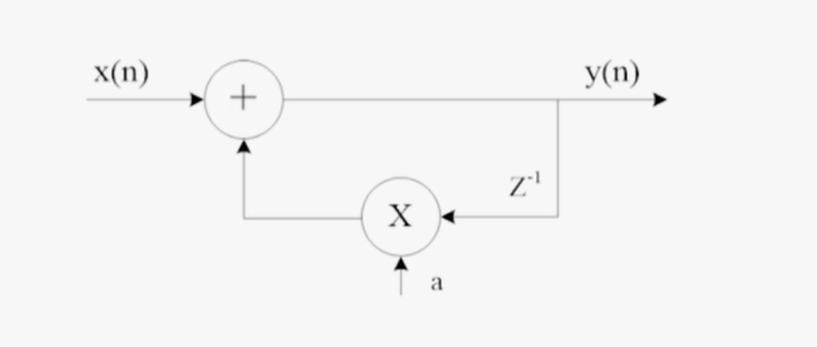
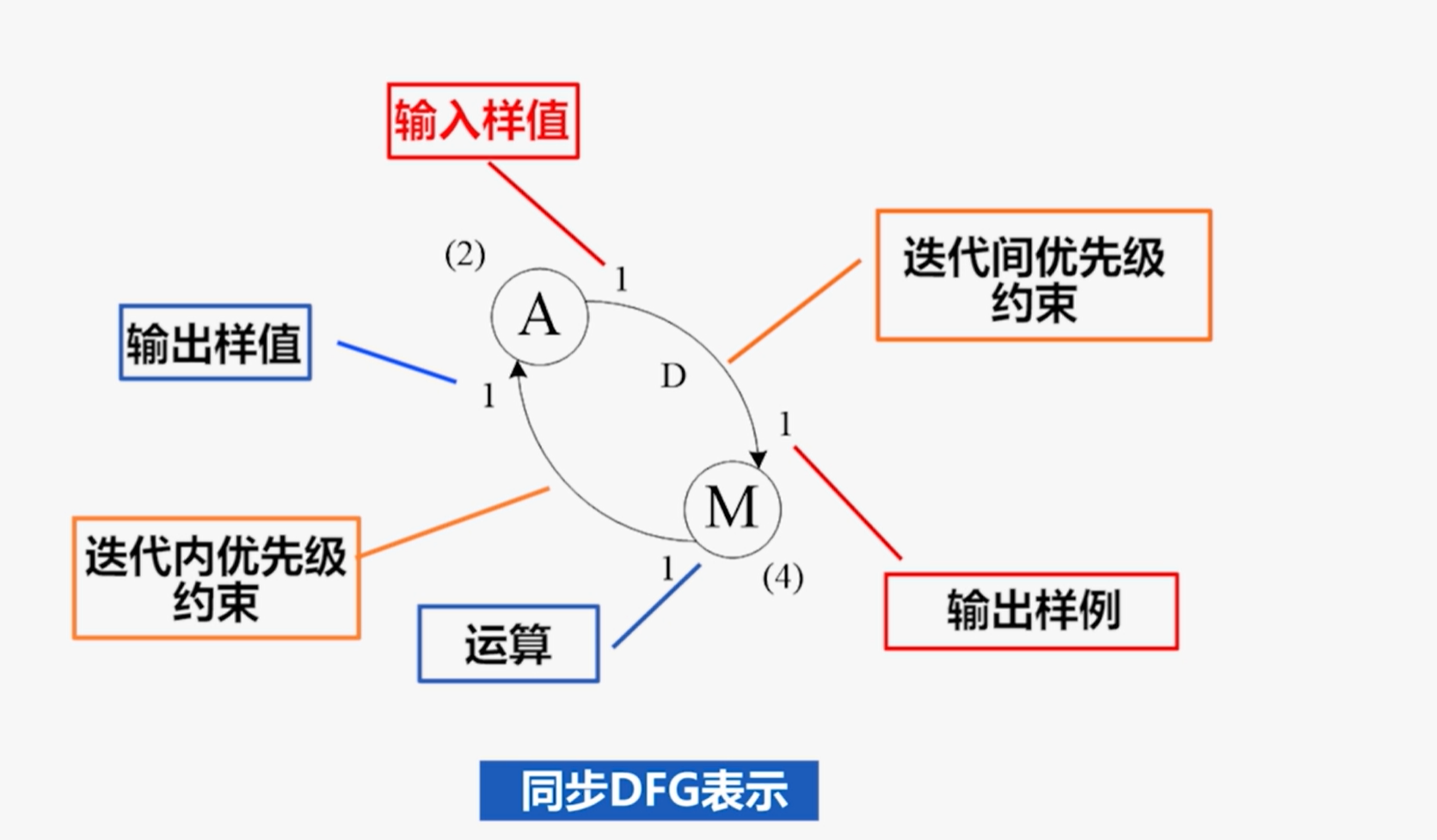
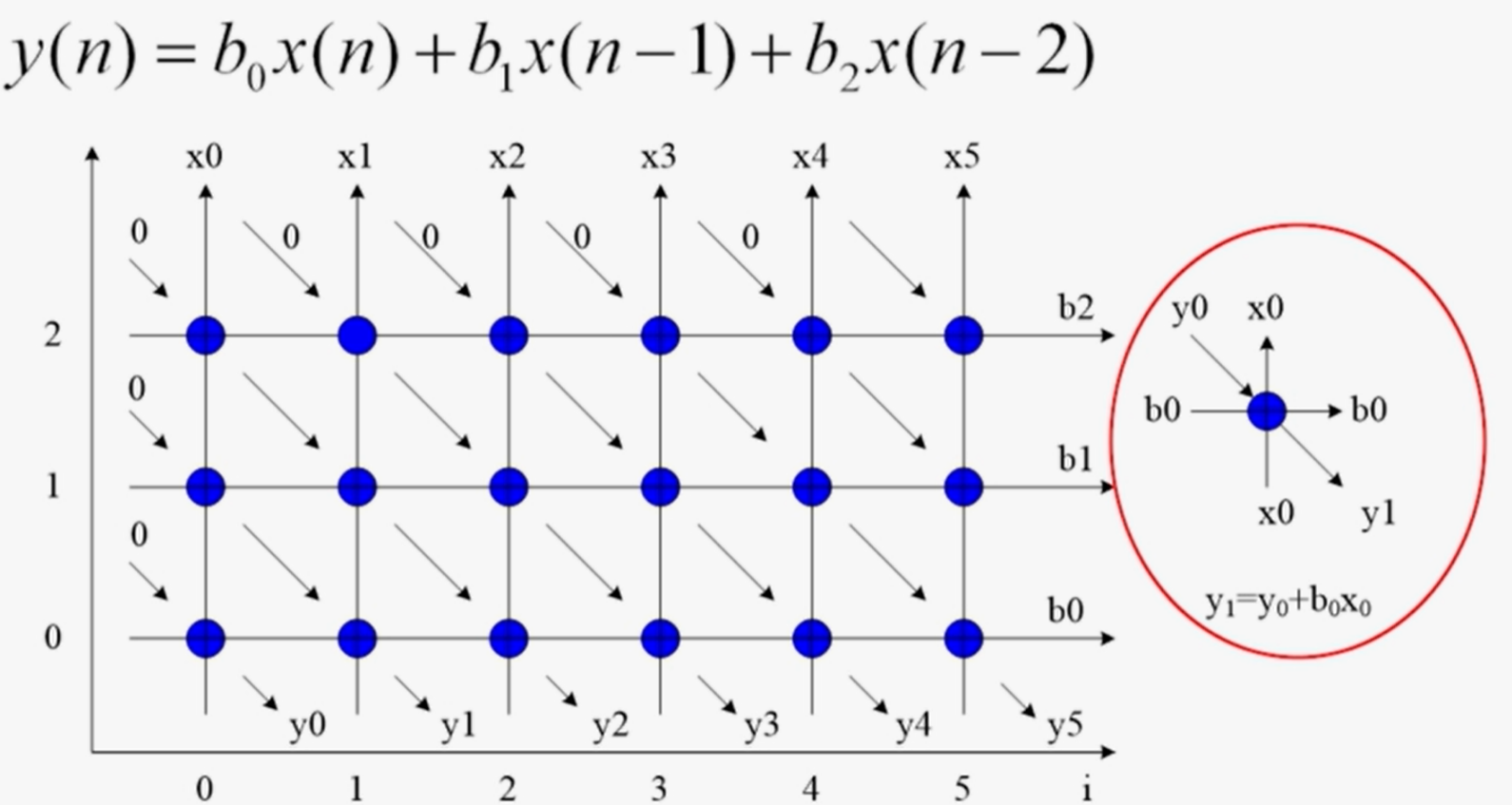
4.依赖图（Dependence Graph）
依赖图是一种有向图，表示算法计算间的依赖关系（脉动阵列常用）
迭代边界
1.基本概念
迭代：DFG中所有节点执行一次
迭代周期$T_{it}$：是处理一次输入样点并输出一个结果所需要的时间
时钟周期$T_{clock}$：系统按拍工作的周期，由关键路径$T_c$决定
系统时钟频率$f$：$f=\frac1{T_{clock}}$
环路：开始与结束于同一节点的有向路径
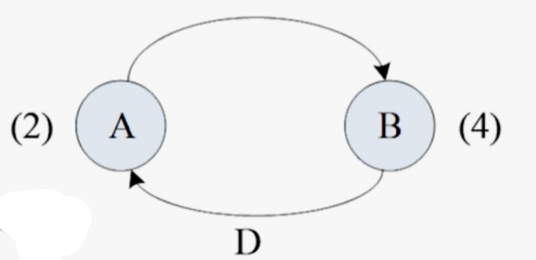
环路边界：第L个环路的环路边界为：
$$
T_{LoopBond}=\frac{T_L}{W_L}
$$
$$
其中,T_L是环路运行时间,W_L是环路中延迟数
$$
关键环路：具有最大环路边界的环路
迭代边界：关键环路对应的环路边界值$T_{\infty}$
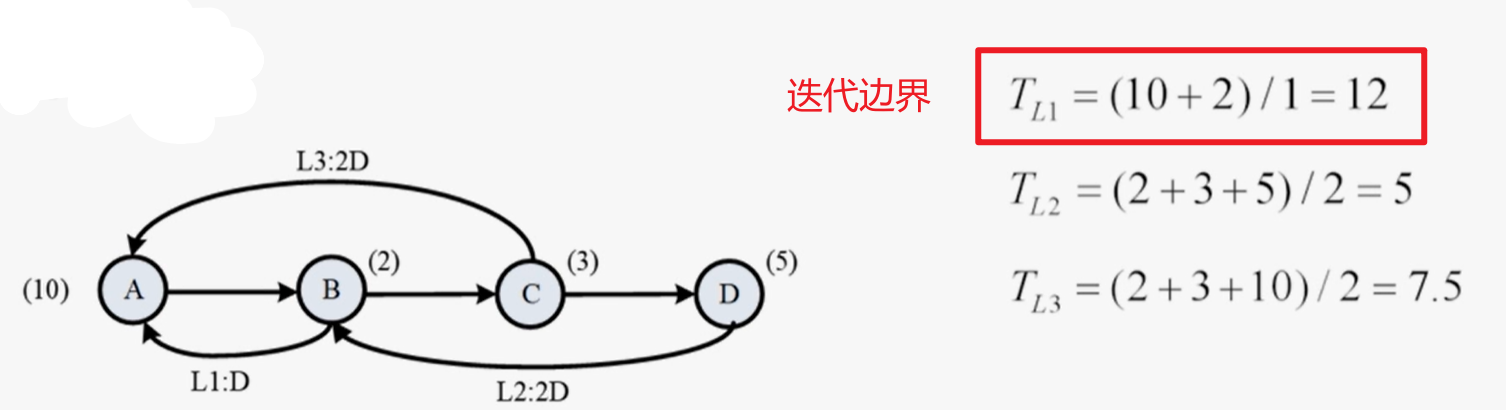
2.迭代边界的特点
- 环路必须有延迟元件
- 必须是因果系统，非因果系统系统无法硬件实现
- 给出DFG所有环路迭代周期的下限
- 决定带反馈环路DSP算法性能的重要参数，反映了硬件实现DSP程序能有多快
- 即使DSP系统无限提高计算能力，迭代周期$\ge$迭代边界
3.最长路径矩阵（LPM）求迭代边界
建立一系列矩阵$L^{(m)},m=1,2,\cdots,d$，取每个矩阵对角线的非-1元素除以寄存器数目，最终求它们的最大值即为迭代边界
$L^{(m)}$中的m表示此矩阵都是包含m-1个延迟的，d为寄存器数
矩阵中元素下标$(i,j)$表示从寄存器$i$到寄存器$j$的包含$m-1$个延迟的最大运算时间
如果这样的路径不存在，那么$L_{i,j}^{(m)}=-1$
具体求解步骤：
先计算$L^{(1)}$：
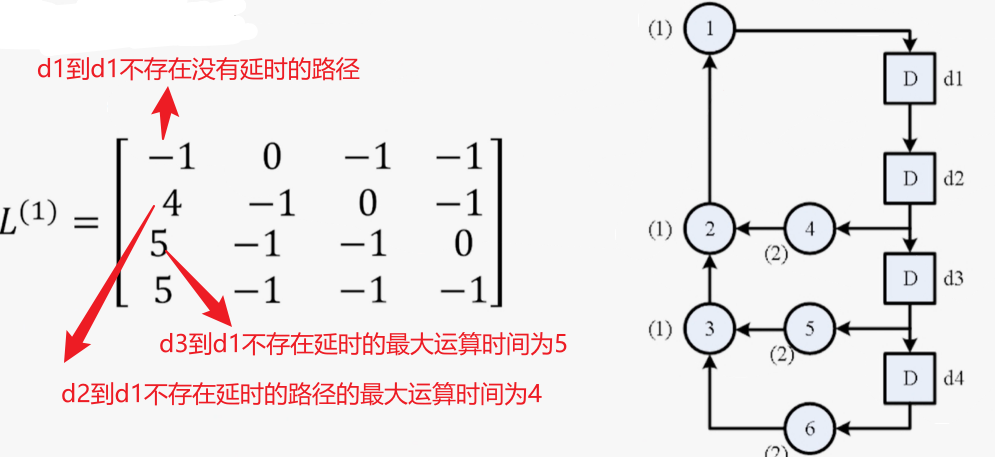
通过如下公式求得其他延时下的矩阵：
$$
L_{i,j}^{(m+1)}=max(-1,L_{i,k}^{(1)}+L_{k,j}^{(m)})
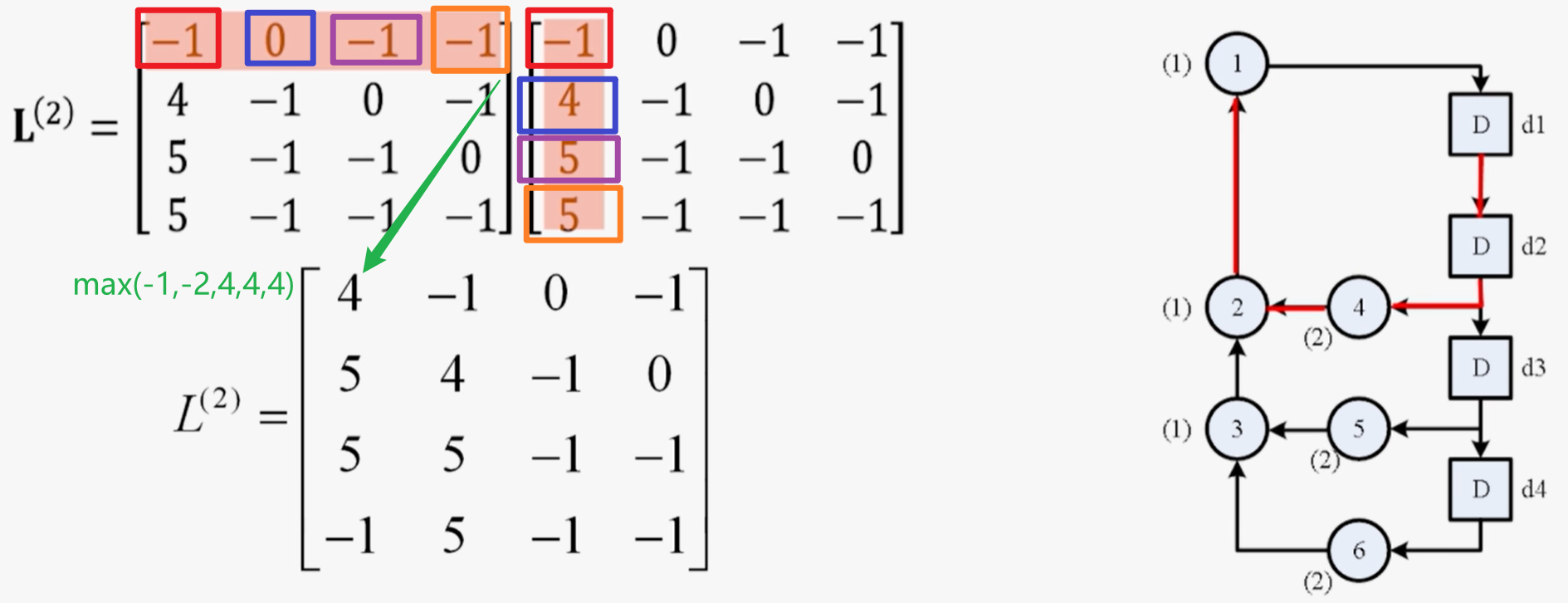
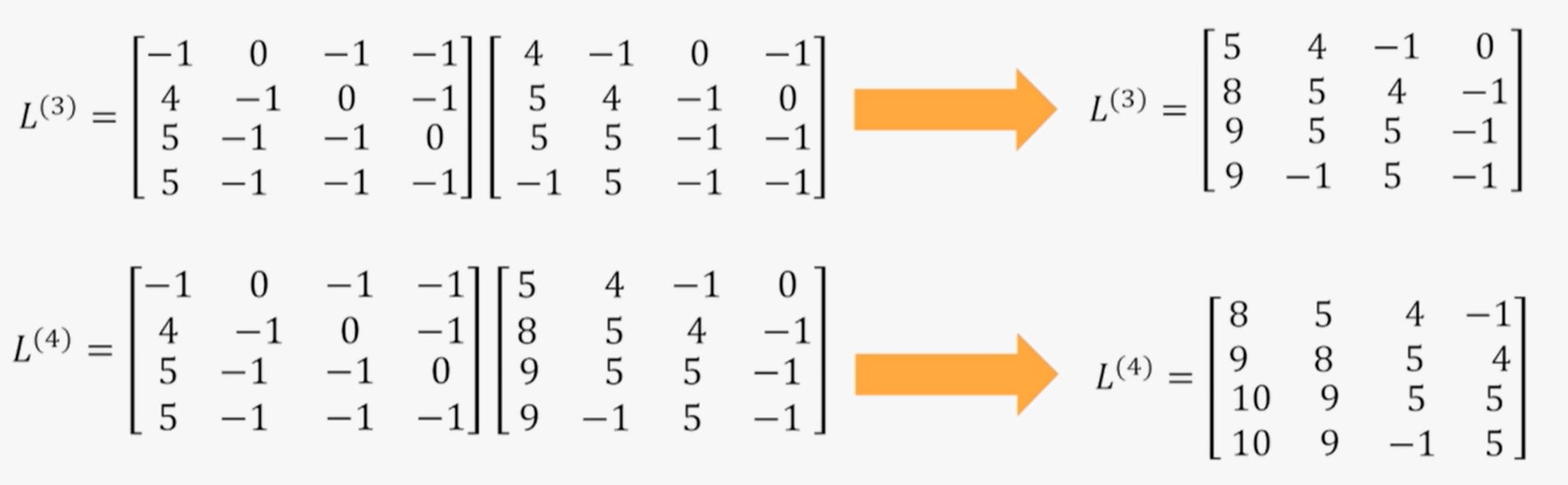
$$
则最终迭代边界为：
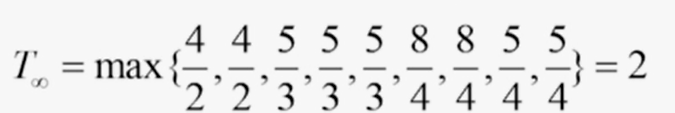
周期相关的基本概念
- 采样周期：
- 输入信号样点间隔的时间
- 取决于应用需要：语言、图像等各不相同
- 迭代周期：
- 完成一次迭代的时间
- 取决于时钟周期和产生输出样点数
- 时钟周期：
- DSP系统工作所用的时钟周期
- 取决于DSP的关键路径
- 关键路径：
- DFG中执行计算时间最长的无延迟路径
