本节主要介绍了运动目标检测及测速的方法,包括多普勒效应测速与信息提取、MTI与MTD、盲速盲相等问题。
多普勒效应及应用
1.多普勒效应
- 多普勒效应是指当发射源和接收者之间有相对径向运动时,接收到的信号频率将发生变化
1.1 连续波雷达
对于连续波雷达而言,收发天线是无法共用的
发射信号:$S_t(t)=Acos(w_0t+\phi)$
回波信号:$S_r(t)=kAcos(w_0(t-\frac{2(R_0-v_rt)}{C})+\phi)$
由于接收信号的频率为:$f_r=f_t+\frac{2v_r}{\lambda}$,带入$S_r(t)$,得到:
1.2 脉冲雷达
发射信号:
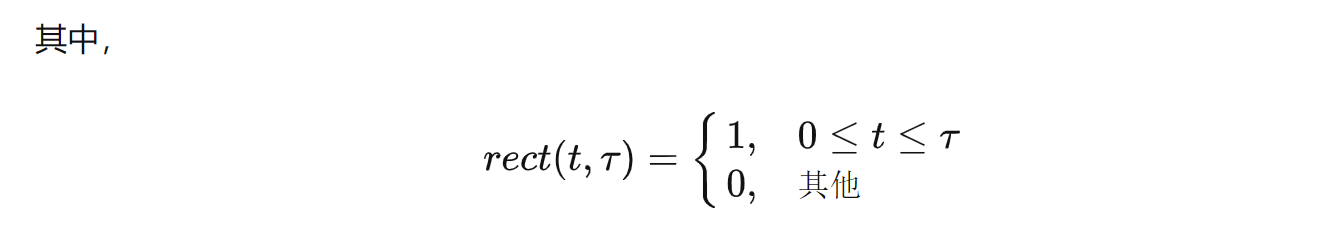
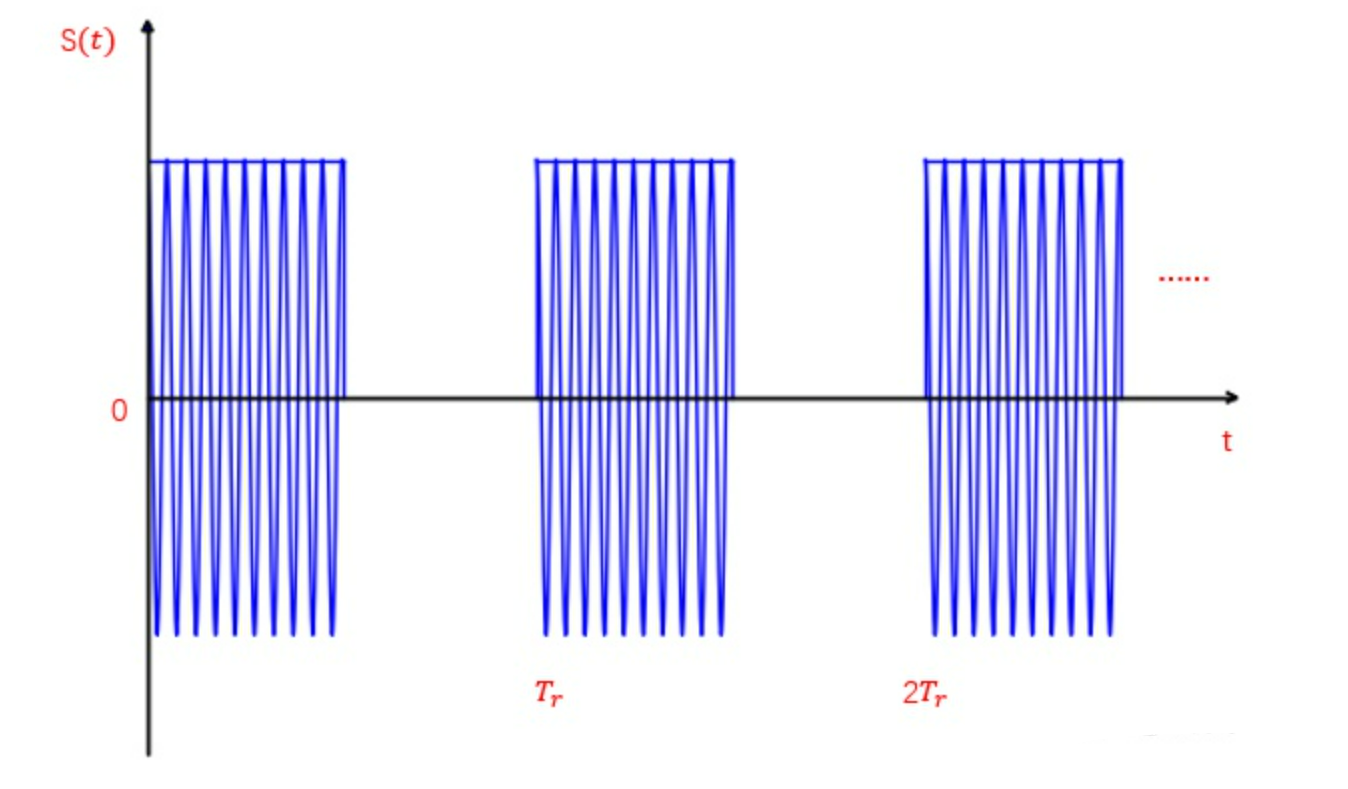
回波信号:
2.多普勒信息的提取
2.1 连续波雷达
就是将发射信号$s_t(t)$和回波信号$s_r(t)$相乘(混频),根据三角公式,将会产生一个高频分量和一个低频分量,然后进行低通滤波就可以得到$f_d$
最后得到的多普勒频率信号为:
2.2 脉冲雷达
$\because$雷达接收信号为:$S_r(t)=\sum_nkArect(t-t_r-nT_r,\tau)cos(2\pi f_0t+2\pi f_dt+\phi-\phi_0)$
将脉冲雷达接收信号与连续波信号$S_t(t)=Acos(w_0t+\phi)$进行混频,得到:
则对于固定目标,$w_d=0$,输出结果为等幅脉冲序列
对于运动目标,$w_d\neq0$,$f_d$相对于$f_r=\frac1{T_r}$比较小,则整个表达式可以看作式连续波充当了周期脉冲的包络,也就是回波脉冲包括调制频率即多普勒频率
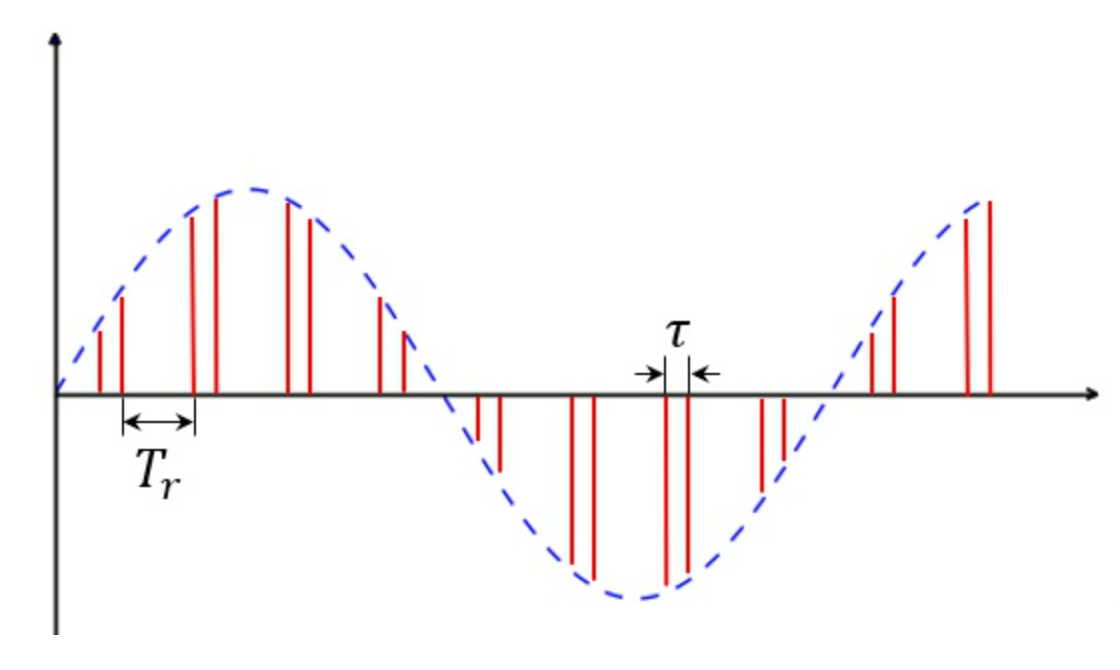
- 对于脉冲雷达,相位检波器输出可以看作是对连续波进行了采样,所以可以通过$FFT$求得$f_d$
3.盲速和频闪
- 当雷达处于脉冲工作状态时,将发生区别于连续工作状态的特殊问题,即盲速和频闪效应
3.1 盲速
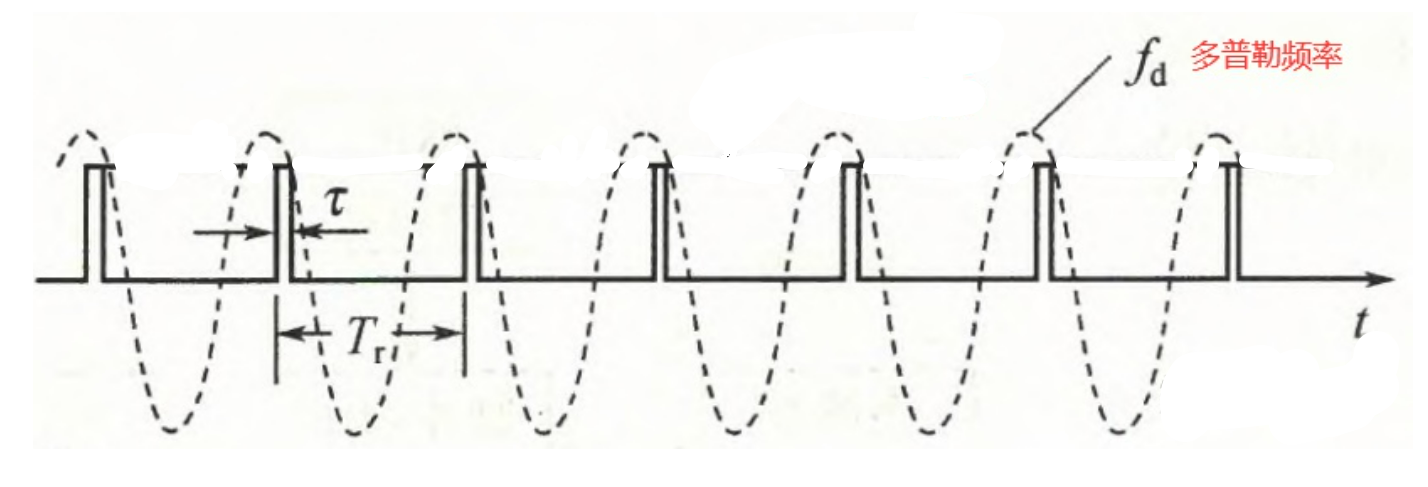
- 当$f_d=kf_r,k=\pm1,\pm2,\cdots$时,就会出现盲速
- 当$k=1$,即$f_d=f_r=\frac{2v_r}{\lambda} \Rightarrow 第一盲速v_r=\frac{f_d\lambda}{2}$
- 当存在盲速时,就需要采取相应的方法消除盲速。所说的消除盲速,并不是指完全将盲速消除,而是增大第一盲速,只要目标速度小于第一盲速,就不会出现盲速
3.2 频闪
当$f_{d1}=nf_r±f_{d2}$时,就会出现频闪现象,直观来讲就是脉冲包络存在多种拟合方式
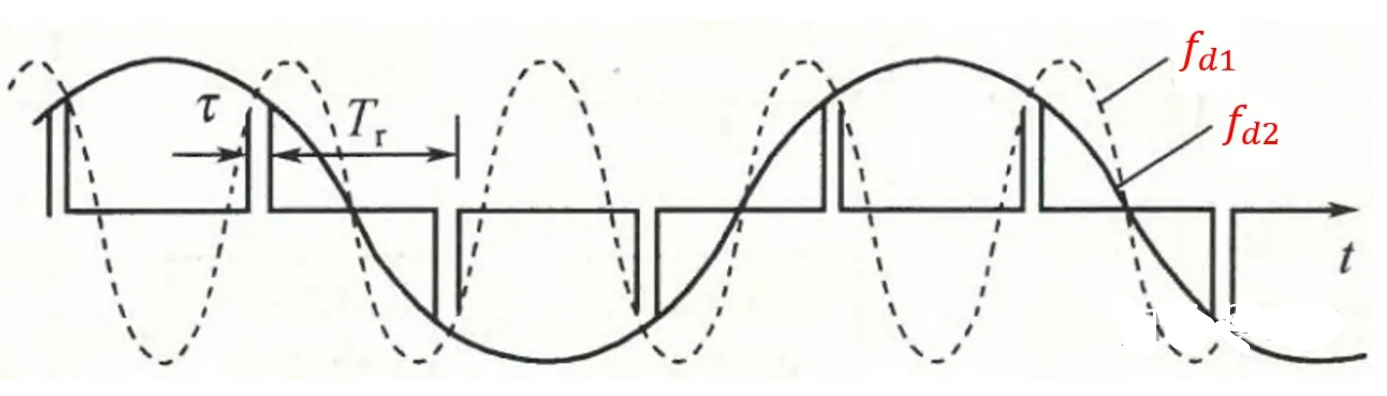
避免频闪需要满足的条件:
- 其中,$f_r$可以看作是对连续波进行采样的频率,$f_d$可以看作是连续波的频率。也就是说,只要满足奈奎斯特采样定理就不会出现频闪
动目标显示雷达MTI
- 经过相位检波之后,去除固定目标的回波,只保留运动目标的回波
1.中频部分进行相检的原理
- 相位检波通常是在中频进行的
- 发射信号的相位:$ω_0t+ϕ$
- 回波信号的相位:$ω_0t+ω_dt+ϕ−ϕ_0$
- 本振信号的相位:$ω_Lt+ϕ_L$
- 发射信号和本振混频之后的相位:$(ω_L−ω_0)t+(ϕ_L−ϕ)$
- 回波信号和本振混频之后的相位:$(ω_L−ω_0−ω_d)t+ϕ_L−ϕ+ϕ_0$
- 相位检波器就是将发射信号的中频和回波的中频再进行混频,再通过低通滤波器就得到$f_d$
- 相位检波之后得到:$ω_dt−ϕ_0$
2.消除固定目标回波
在相位检波器输出端,固定目标的回波是一串振幅不变的脉冲,而运动目标的回波是一串振幅调制 的脉冲。据此,将相位检波器输出通过相消器,就可以消除固定目标回波,保留运动目标回波
一次相消器:
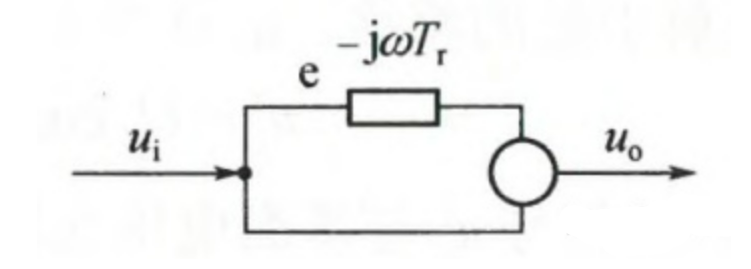
对于固定目标的回波,脉冲多普勒雷达经过相位检波之后的输出为一串等幅脉冲,脉冲间隔为$T_r$。如果脉冲序列足够长,将其迟延$T_r$之后得到的脉冲序列,和原来的脉冲序列将会重合到一起,将两个相减输出$Δu=0$
对于运动目标,除开盲速的情况,输出$Δu≠0$
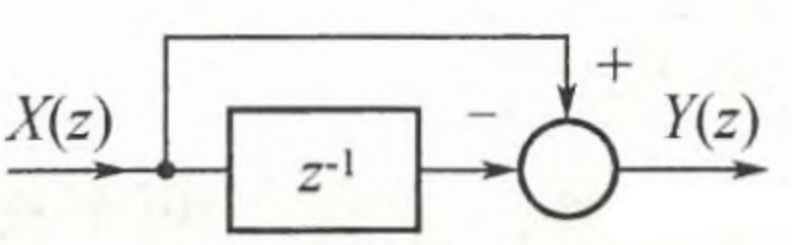
有:$u_o=u_i-u_ie^{-jwT_r}$
其传递响应函数为:
- 其幅频特性为:
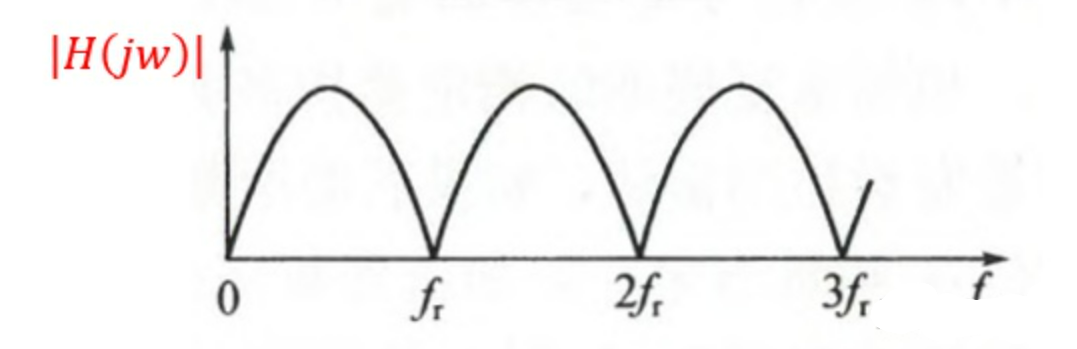
- 其幅频特性为:
从幅频特性角度来看,$|H(jω)|$就是一个滤波器,相当于将$f_d=0$的固定目标,及以盲速运动的目标就全部过滤掉了
盲速、盲相的影响及其解决途径
1.盲速
盲速是指目标实际上有运动速度,但对于雷达来说经过相检之后的输出和固定目标相检之后的输出都是等幅的脉冲串,导致无法区分
当目标的多普勒频率满足:$f_d=nf_r,n=\pm1,\pm2,\cdots$时就会产生盲速
第一盲速$v_r=\frac{\lambda f_r}2$
要想不出现盲速,并不是要彻底消除盲速问题,是要想办法将第一盲速的值扩大
从公式可知,只要增大$f_r$就可以增大$v_r$,但是,$f_r$增大,$T_r$就减小,就与无模糊距离矛盾了,即增大$f_r$虽然使第一盲速增大了,但是最大无模糊距离就减小了
可以采用重频参差的方法扩大第一盲速,对于两重频,有:
2.盲相
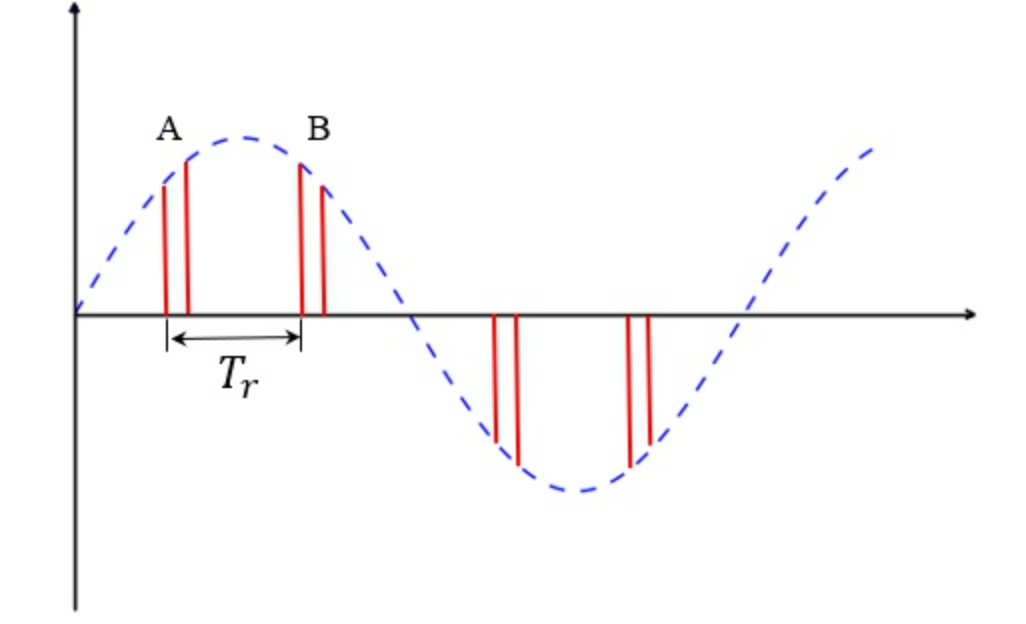
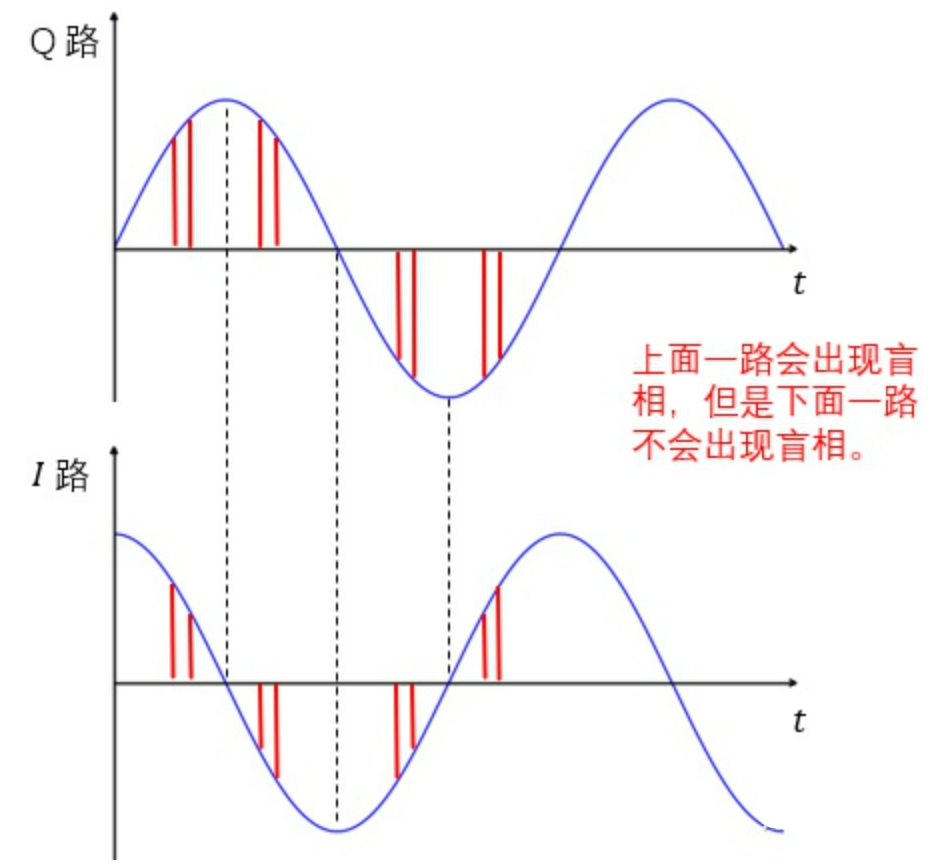
$A$点和$B$点幅度相同,经过相消器处理,就是将图形迟延$T_r$,从图上来说,就是将$A$点移到了$B$点,然后再相减,$B$点就减为$0$了,这一点的相位信息也就损失掉了。这种情况称之为点盲相
出现原因:相检过后某一特殊时刻,前后间隔$T_r$是等幅的,消相器将其当作了静止目标,将其消掉
解决办法:先消相再相检(中频对消)
不通过相位检波器,直接将中频输出结果进行对消
中频输出$u_{r1}$:
- $w_i$为中频角频率,只写出了连续波信号部分,实际上这里应该是以连续波为包络的一个个脉冲串
将$u_{r1}$延迟$T_r$后得到:
将$u_{r1}$和$u_{r2}$进行对消之后得到:
对消的目的就是将固定目标回波相除,即在$f_d=0$时,使对消器输出$\Delta u=0$
对于固定目标而言$f_d=0$,想要在中频进行对消(即消除固定目标回波),$f_i$就不能随便选,需要满足如下条件:
此外,还可以通过零中频的方式解决盲相,其思路是: $I,Q$双通道处理,正交双通道由两路相同的支路组成,差别只是其基准的相参电压相位差 90°,这两路分别称为同相支路( I 支路)和正交支路( Q 支路)。
回波和杂波的频谱及动目标显示器
- 运动目标检测的任务就是根据运动目标回波和杂波在频谱结构上的差别,从频率上将它们区分,以达到抑制固定杂波而显示运动目标回波的目的
1.雷达回波信号的频谱
雷达回波:
回波频谱:
接收信号的幅频特性和发射信号的幅频特性基本相同,只是优于回波多了一个$k$导致其幅频特性的高低有差别。如果目标运动,接收信号和发射信号的载频就相差一个多普勒频率$f_d$。所以,只要将发射信号的频谱分析清楚就能得到接收信号的频谱
雷达发射相参脉冲串,其脉冲宽度为$τ$,脉冲重复频率为$f_r$。当天线不扫描而对准目标时,所得脉冲为无限脉冲串。此时,雷达发射信号为:
其中:
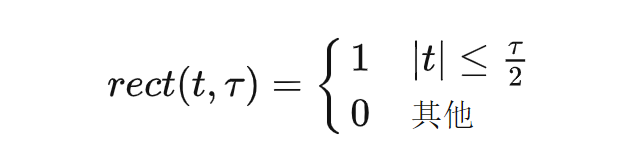
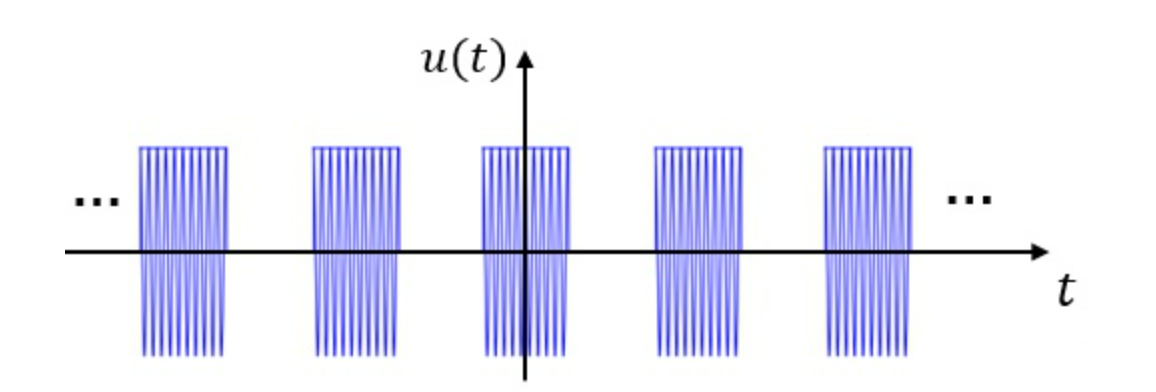
可以先不考虑后面的余弦项,只考虑$rect$项,如下所示。最后乘以$cos$项,相当于将$rect$项的频谱进行搬移即可得到$u(t)$的频谱
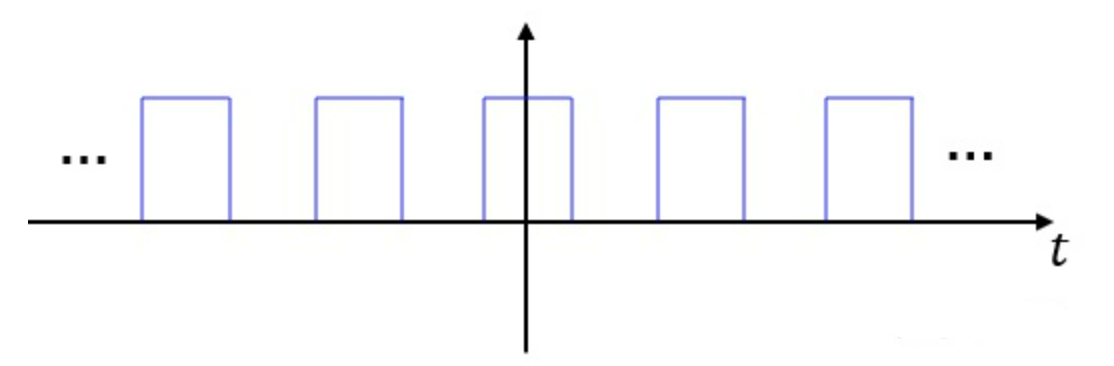
周期函数的傅里叶变换是通过傅里叶级数来实现的,周期函数的傅里叶级数是一根根离散的$\delta$函数,$\delta$函数的间隔就是周期的倒数。$\delta$函数的包络就和一个周期内部的信号的傅里叶变换有关。门函数的傅里叶变换是一个辛克函数,所以这些 delta 函数的包络就是辛克函数。如下图所示,幅频特性是取了绝对值的,所以图中只有正值没有负值
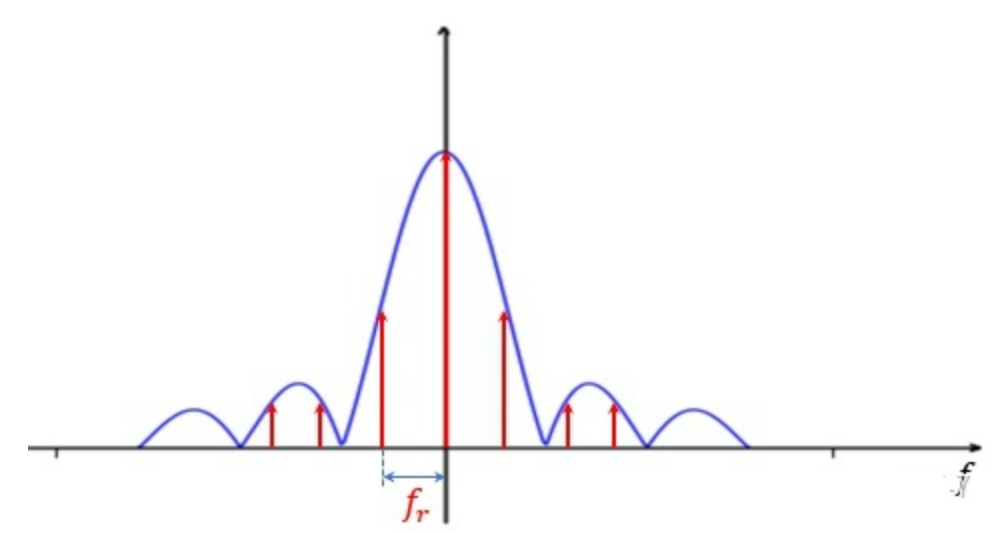
最后,将$rect$项乘以$cos$项,相当于将上述频谱往左右搬移,得到:
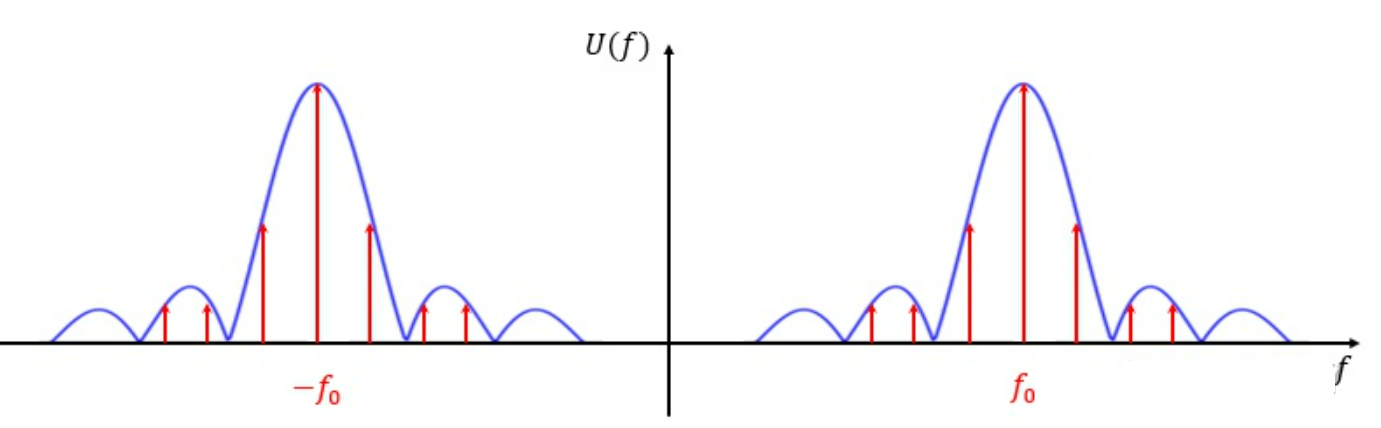
雷达工作时,天线总是以各种方式进行扫描。这时收到的回波脉冲为有限数,且其振幅受天线方向图调制。雷达实际的接收信号可表示为:
其中,$m(t)$为天线的扫描函数,实际就是一个高斯函数,图形如下所示。注意,天线方向图是角度$θ$的函数,扫描的过程就是$θ$随$t$线性变化的过程
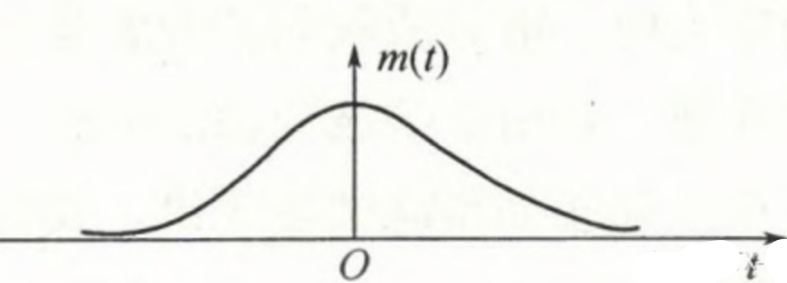
则回波信号$u_m(t)$的频谱:
其中:$\ast$表示卷积
天线的扫描函数$m(t)$的频谱为:$M(f)=e^{-\frac{f^2}{2\sigma^2}}$
$\sigma=\frac{0.256f_r}{n}$
$n$表示在天线扫描期间接收到的回波脉冲个数
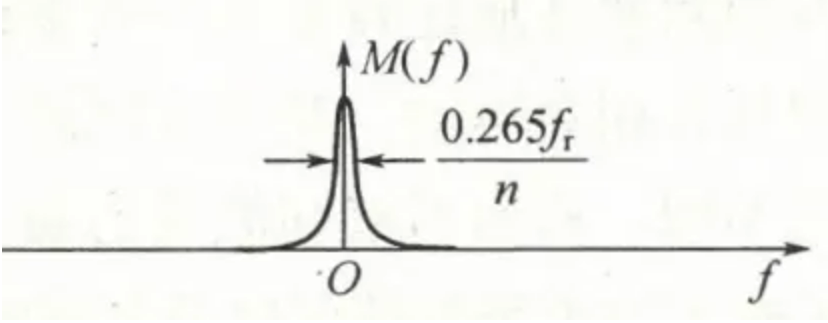
因此,回波信号的频谱就是$M(f)$和一串$\delta$谱线的卷积,相当于将$M(f)$搬移到每根$\delta$谱线位置
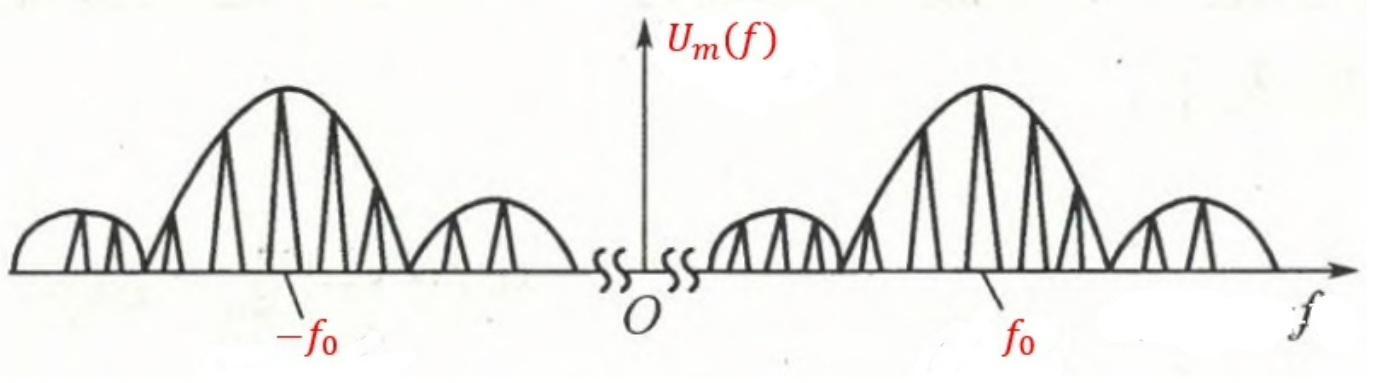
如果目标在运动,接收信号相对于发射信号就会存在一个多普勒频率$f_d$,因此,对于动目标接收信号频谱为:
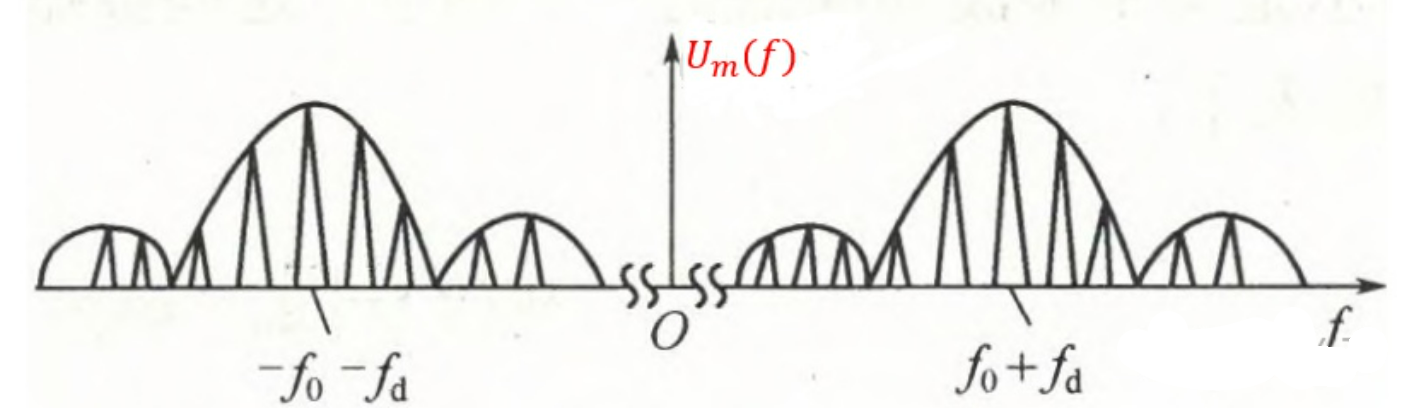
回波中频对应的频谱:
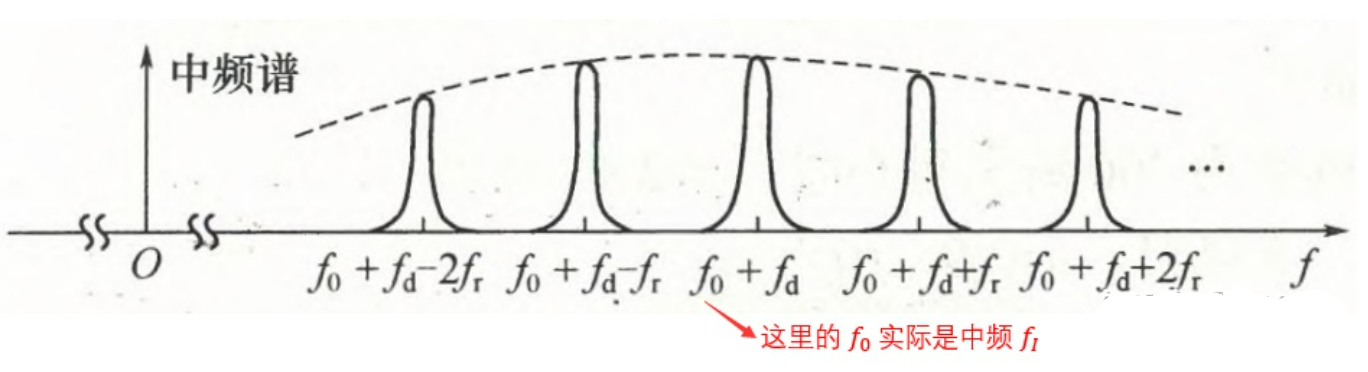
对中频信号进一步进行处理,相位检波器将中频回波和相干电压进行相干检波后(图中虚线表示单路相位检波所产生的频谱折叠情况,是由负频率轴频谱差拍而产生的):
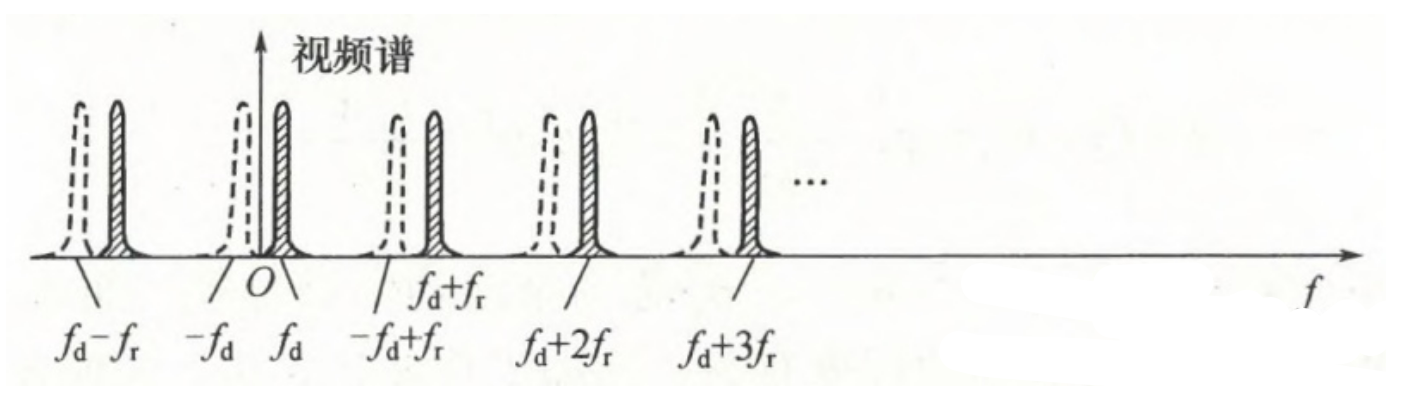
实际在处理的时候,通过得到$e^{jω_0t}$这样的信号从而消除虚线部分,可以利用$I,Q$双路处理。一路$cos(ω_0t)$表示信号的实部,另外一路$sin(ω_0t)$表示信号的虚部,就可以得到$e^{jω_0t}$。再进行相干检波出来的结果,就只有$nf_r+f_d$
2.杂波的频谱
3.动目标显示滤波器
动目标显示滤波器利用运动目标回波和杂波在频谱上的区别,可有效地抑制杂波而提取信号
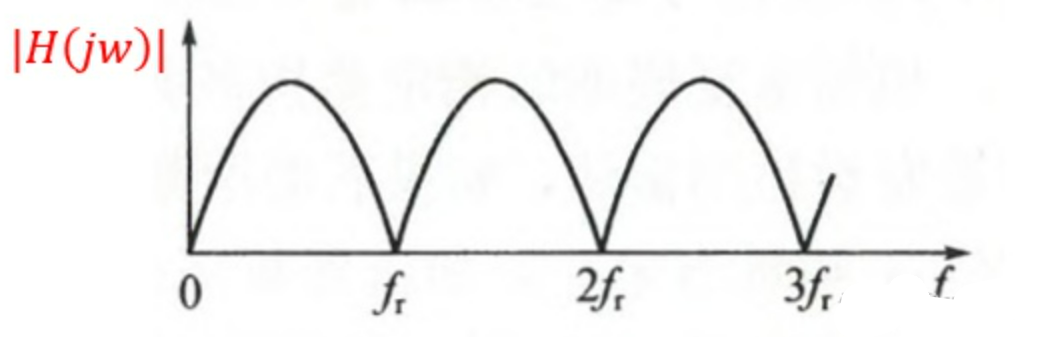
在脉冲雷达中MTI滤波器就是利用杂波与运动目标的多普勒频率的差异,使得滤波器的频率响应在杂波谱的位置形成“凹口”,以抑制杂波,而让动目标回波通过后的损失尽量小或没有损失
动目标检测MTD
- MTD是在MTI的性能基础上进一步完善和提高
1.动目标检测的特点
动态范围更大
改善因子提高
- 需要和噪声系数的定义区别开,噪声系数的定义是输入的信噪比与输出的信噪比的比值
- 改善因子的定义是,输出信杂比与输入信杂比的比值
- 主要体现在对杂波的改善上。通过动目标检测雷达合理的设计,可以使得输出的杂波比输入的杂波要小,即将杂波消除的更多一些
增加多普勒滤波器组
- 对动目标检测雷达来讲,通过滤波器组将运动目标多普勒频率测量出来。
抑制地杂波
增加杂波图
- 不同地方的地物杂波是不一样的。
- 相当于把不同区域的地物杂波的特性存储下来,对于杂波比较强得地方,把杂波门限提高,对杂波比较弱的地方门限降低
- 有了杂波图之后,相应的门限就不再是一个固定门限,检测起来就有一定的灵活性
2.多普勒滤波器组
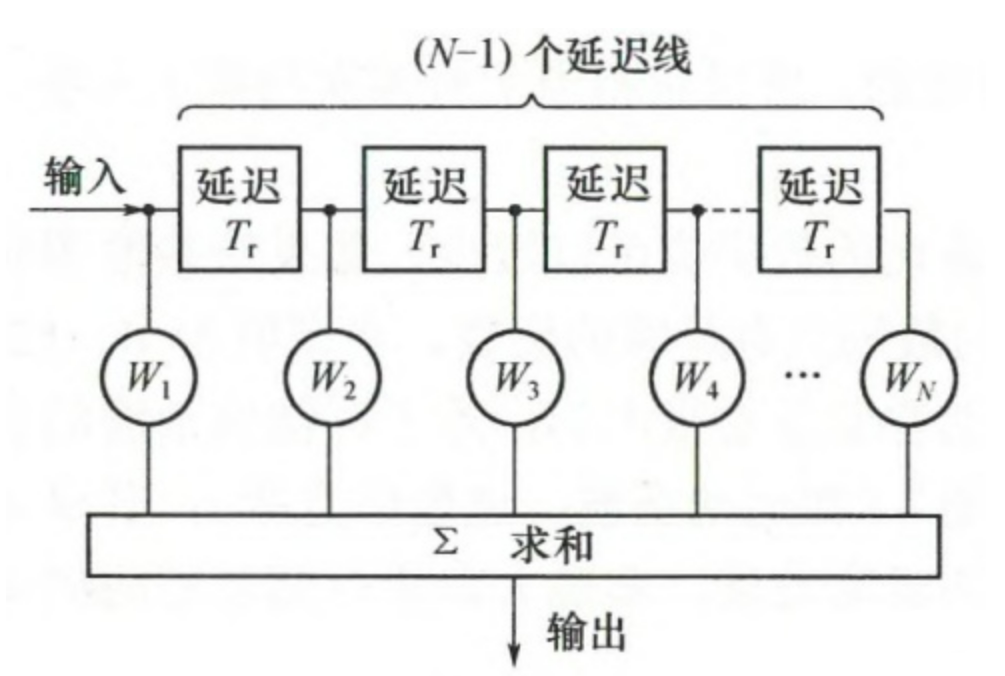
多普勒滤波器组就是用来测量多普勒频率的
其输入就是相位检波之后的输出信号
横向滤波器的总输出:
每一个值实际上对应的是一个频率,$0$对应的频率是$\frac0Nf_r$,$1$对应的频率是$\frac1Nf_r$,$2$对应的频率是$\frac2Nf_r$以此类推。
求出所有$X(k)$之后,找出$X(k)$里面哪一个$k$对应的值最大,频率就是$k$对应的频率,该频率就是回波脉冲的包络调制频率即多普勒频率,根据多普勒频率就可以求得目标的速度
CFAR检测算法
- 干货 | FMCW雷达信号处理的二维CFAR(2D CFAR、十字CFAR)检测算法 - 知乎 (zhihu.com)
- 雷达系统必备知识——恒虚警检测器CFAR (zhihu.com)
- CFAR(恒虚警率)目标检测算法_cfar检测_huhaoming-dd的博客-CSDN博客
