本节主要介绍了雷达目标角度测量的基本方法,包括相位法与振幅法,以及圆锥扫描自动测角系统与单脉冲自动扫描测角系统。
天线方向图的一般性质
雷达天线方向函数:
- 其中$|F(\theta)|$是天线方向图函数的振幅响应
- $\phi(\theta)$是天线方向图函数的相位响应
只考虑振幅响应,有:
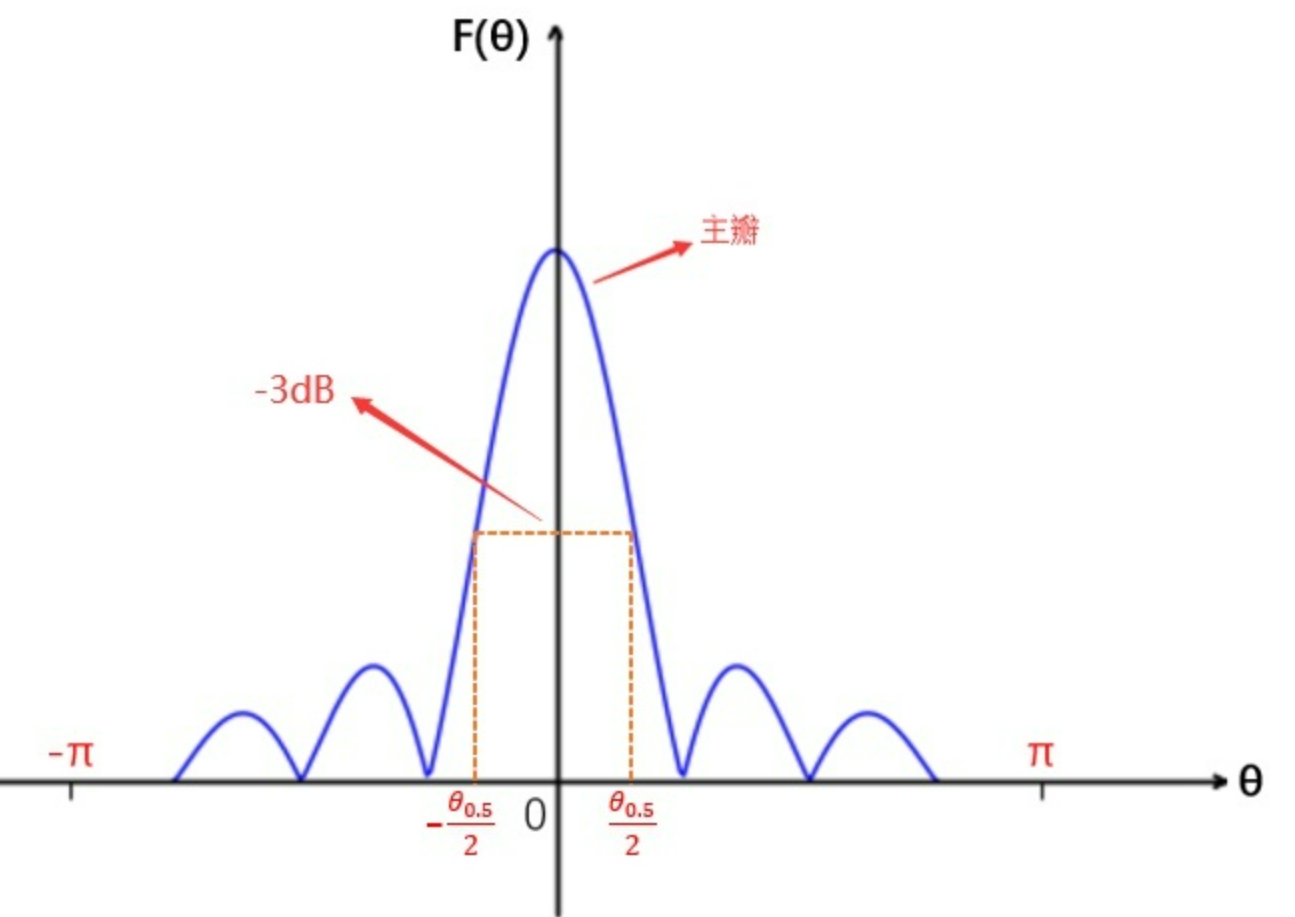
- $F(0)\ge F(\theta),∀θ∈[−π,π]$
- $F(\theta)=F(-\theta)$
- $|\theta_1|>|\theta_2|,且\theta_1,\theta_2在主瓣内,则F(\theta_1)<F(\theta_2)$
- $\frac{F_电(\frac{\theta_{0.5}}{2})}{F(0)}=\frac{\sqrt2}2$
- $F_{功-t}(\theta_1)=F_{电-t}^2(\theta1)$
- $F_{功-r}(\theta_1)=F_{电-r}^2(\theta1)$
相位法测角
1.两天线相位法测角原理
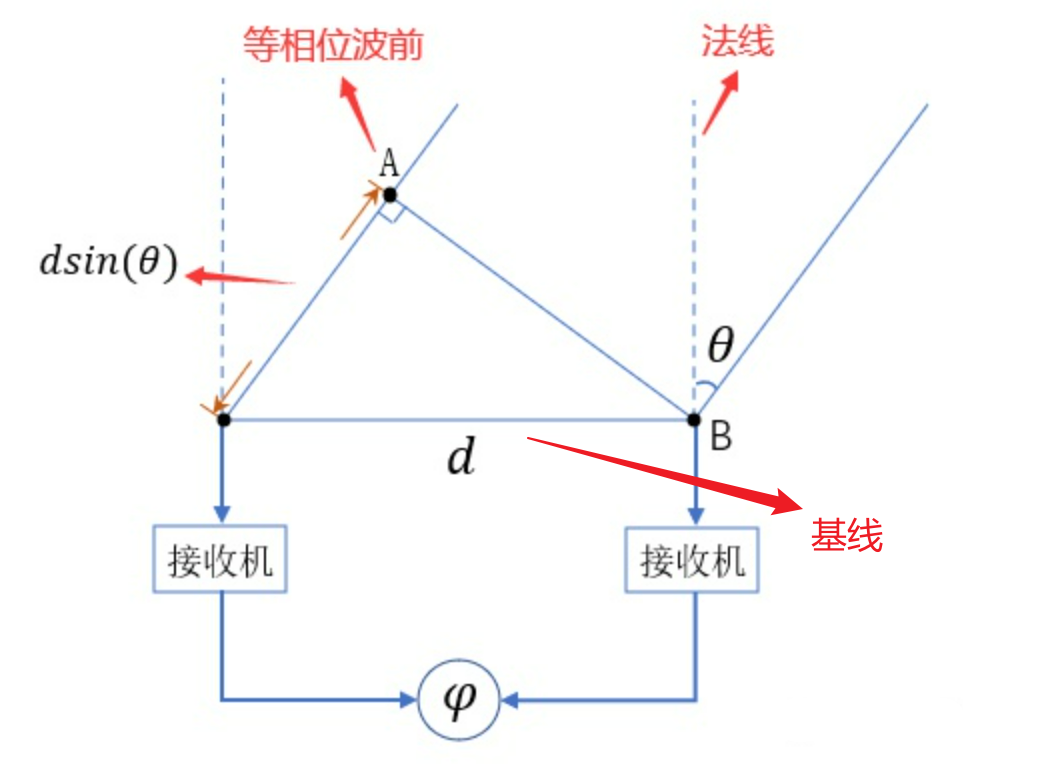
假设两天线之间的距离$d$,远远小于目标到振源的距离,则可以认为到达接收点的目标所反射的电磁波近似为平面波。
目标到$A,B$两点的距离相等,回波到$A,B$两点的相位也相等,回波到接收点的距离相差$dsin(θ)$,对应相位相差$\phi$,有:
则测量相位差$\phi$就能测量角度了
当$ϕ∈[−π,π]$时,$θ$取值无模糊。$θ$对应的取值范围$[−θ_{max},θ_{max}]$,由$\phi=\frac{2\pi dsin\theta}{\lambda}$可得:
从上式可知,只要$d$越小,对应的$θ_{max}$就越大。则短基线保证大的无模糊测角范围。
2.测角误差分析与多值性
对$\phi=\frac{2\pi dsin\theta}{\lambda}$两边同时微分,有:
采用读数精度高($dϕ$小)的相位计,可以提高测角精度
增大$\frac dλ$的值,即长基线保证高的测角精度
$\theta=0°$时,$d\theta$最小
- $\theta=\pm90°$时,$d\theta$最大
3.多基线测角
- 短基线保证最大无模糊测角范围;长基线保证高的测角精度,故采用多基线测角结合二者优点。
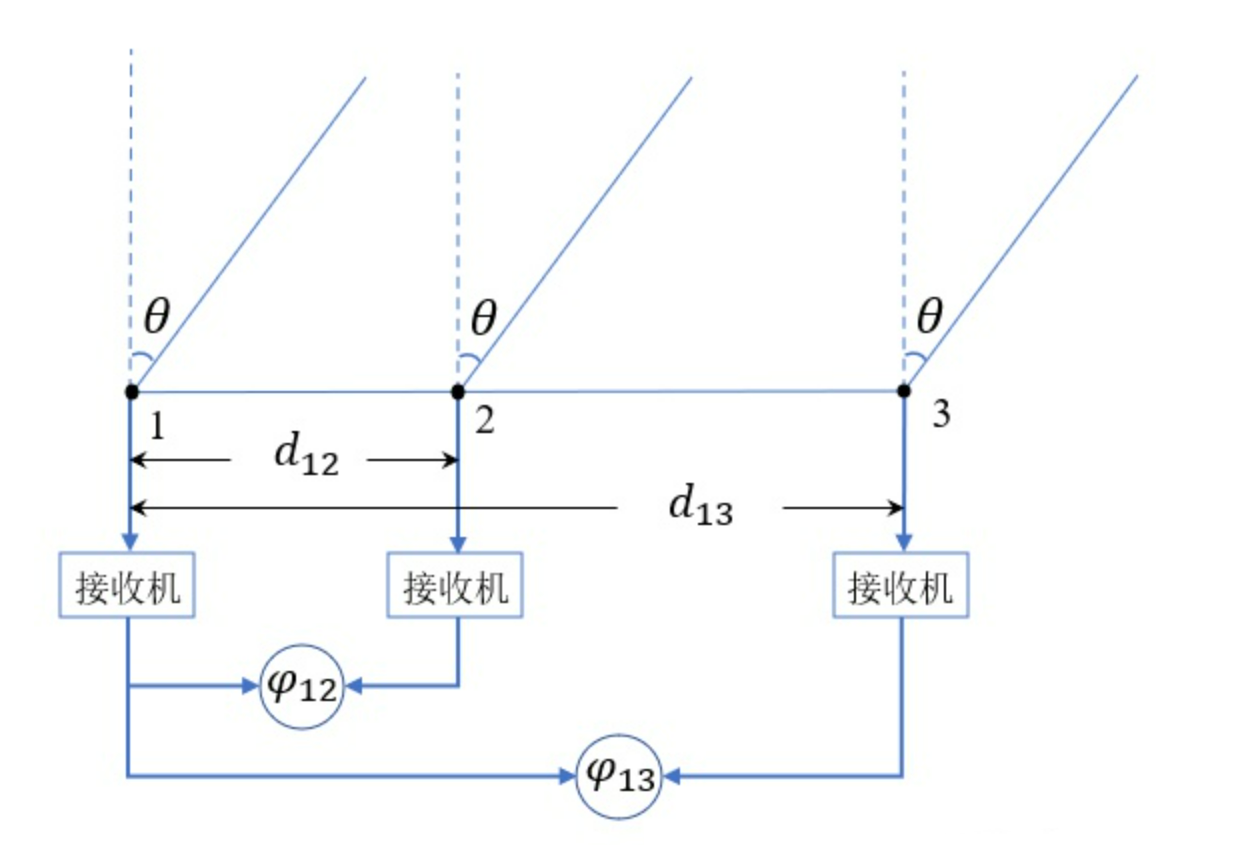
$1$和$2$之间的间距$d_{12}$比较短,$θ_{max}$ 就比较大,以保证比较大的无模糊测角范围,长基线$d_{13}$保证高的测角精度,有:
要使$ϕ_{12}$无模糊测角,$ϕ_{12}$就不能超过$2π$。因此,$ϕ_{12}$就是鉴相器能测出来的值。对于$ϕ_{13}$来讲,因为$ϕ_{13}$比较大,所以 $ϕ_{13}$一般大于 $2π$,有:
因为长基线$d_{13}$算出来的$θ$精度更高,所以有:
式中,$λ$和$d_{13}$已知。因为只能测得$ϕ$,而$N$不知道,所以$ϕ_{13}$未知。只要求得$N$,就可以求出$ϕ_{13}$
将$\phi_{13},\phi_{12}$相比,有:
上式中的$ϕ$是可测量的,其值满足$ϕ<2π$。因此,$\frac{ϕ}{2π}<1$,则$N$:
根据已知的$ϕ_{12},d_{13},d_{12}$,可以求出$N$,进而可以得到$ϕ_{13}=2πN+ϕ$。最后根据公式$\phi_{13}=\frac{2\pi d_{13}sin\theta}{\lambda}$就可以求得$θ$:
振幅法测角
- 振幅法测角是用天线收到的回波信号幅度值来做角度测量的,该幅度值的变化规律取决于天线方向图以及天线扫描方式
- 振幅法测角可分为最大信号法和等信号法两大类
1.最大信号法
- 天线扫描的过程就是雷达天线方向图函数最大值指向不断发生变化的过程
- 如果把从扫描起始时刻到扫描结束时刻,雷达收到目标回波的幅度作图,其幅度的变化过程就类似于天线方向图函数的变化过程,开始比较小,然后逐渐增大,到最大值再慢慢减小
- 最大信号法就是在找幅度变化过程中的极大值所在的位置
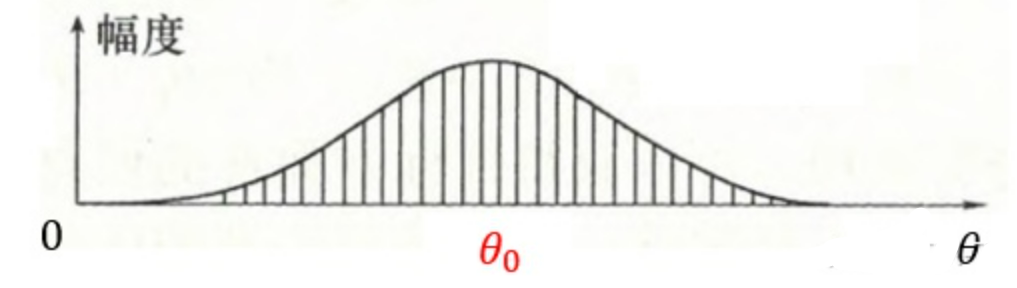
波束宽度、信噪比都会影响最大信号法测角的精度,测角精度满足如下公式:
其中,$θ_B$为天线波束宽度,$(\frac SN)_m$为中心脉冲的信噪比,$n$为单程半功率点波束宽度内的脉冲数。
2.等信号法
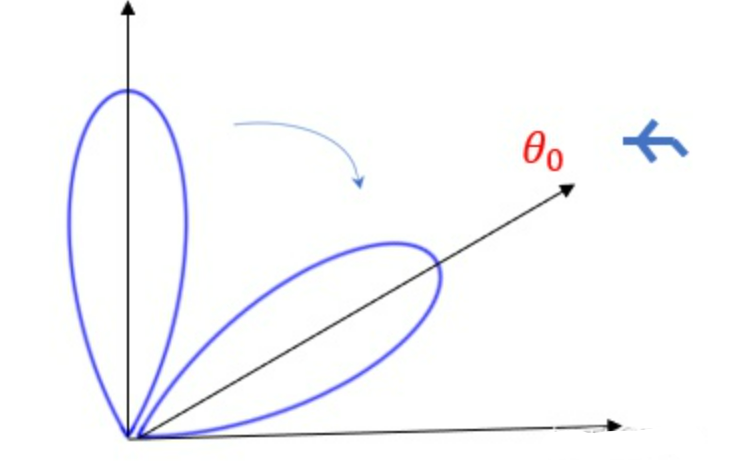
- 等信号法测角釆用两个相同且彼此部分重叠的波束,两个天线方向图交叠处大概在 3dB 点处
- 如果目标处在两波束的交叠轴方向,则由两波束收到的信号强度相等,否则一个波束收到的信号强度高于另一个
- 故常常称 0A 为等信号轴。当两个波束收到的回波信号相等时,等信号轴所指方向即为目标方向
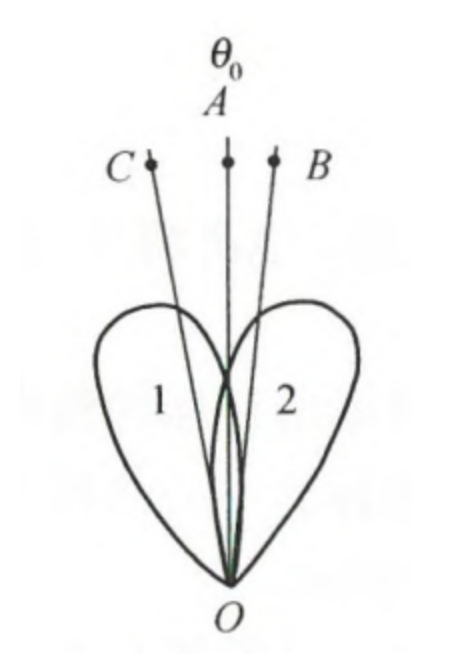
- 设天线电压方向性函数为$F(θ)$,等信号轴$OA$的指向为$θ_0$,$\theta_k$为$\theta_0$与最大方向的偏角,有:
假设$\theta_t=\theta-\theta_0$为目标与等信号轴的夹角,则有:
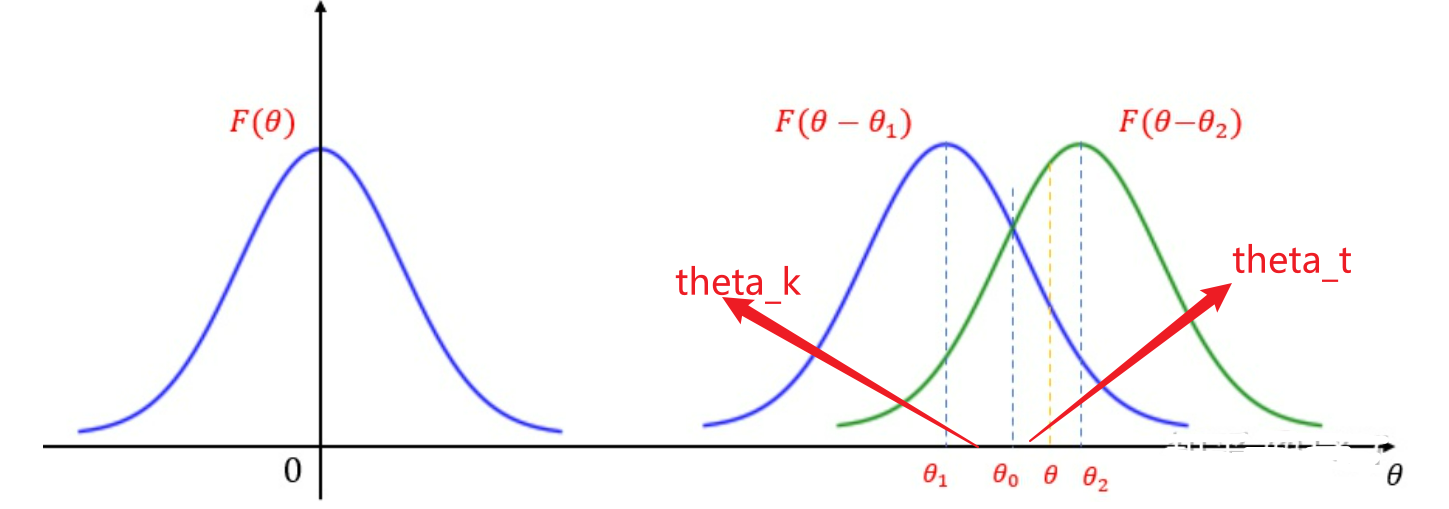
- 故只要求得$\theta_t$就可以得到$\theta$
2.1 比幅法
根据雷达方程可以算得到达天线口面的回波信号功率,然后开方就可以得到幅度,因为两个相同且彼此部分重叠的波束的雷达方程中只有$F(\theta)$不同,其他相同部分均用用$K$统一表示,则有:
比幅法就是将二者相比,得到:
式中,$u_1$和$u_2$是可以测量出来的值;$θ_k$为天线方向图最大值与等信号轴夹角已知。只有$θ_t$是未知量,因此可以求得最终角度
2.2 和差法
和信号为两个天线接收到信号之和,差信号为两个天线接收到信号之差
差信号:
在$\theta_0$附近做级数展开,得到:
和信号:
将和、差信号相比:
只有$θ_t$是未知量,因此可以求得最终角度
自动测角的原理与方法
1.圆锥扫描自动测角系统
- 圆锥扫描波束
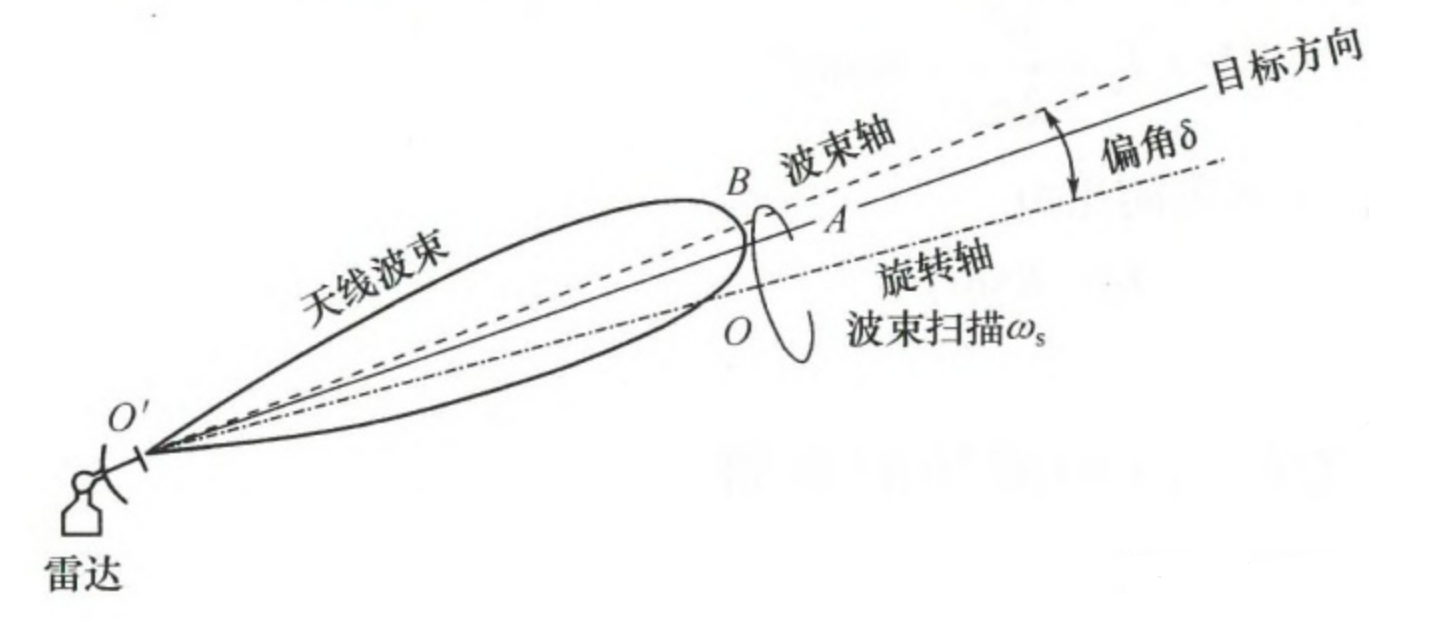
- 垂直于等信号轴的截面
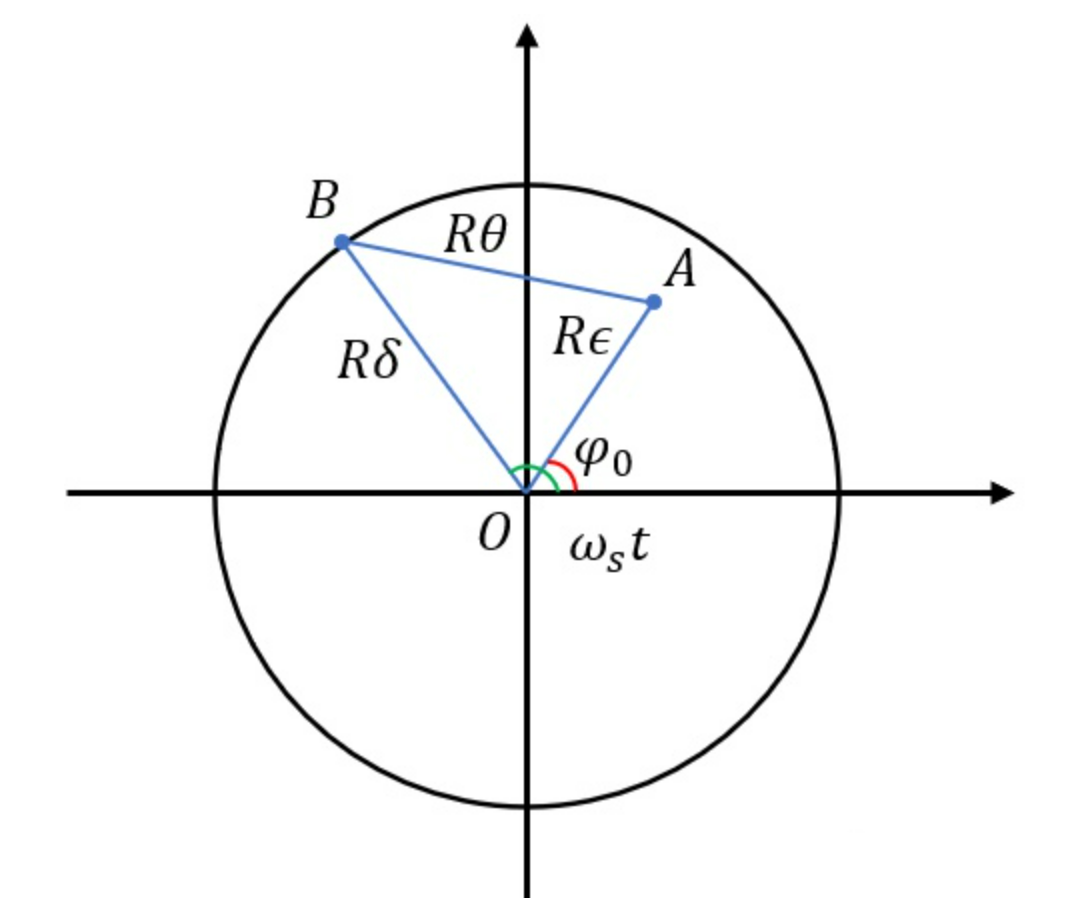
$\delta$:对应前面的$θ_k$,即等信号轴与波束最大值方向的偏角。
$ϵ$:对应前面的$θ_t$,即目标与等信号轴的夹角,是自动测角系统想要测量的值。只要$ϵ$不为 0 ,就要调整旋转轴的指向,使其指向目标的方向。
$θ$:表示目标方向与波束最大值方向的夹角
接收信号电压振幅大小为:
- 根据雷达方程推导,$K$包含了距离、功率等因素
- 如果目标与天线最大增益处的夹角为$θ$,假设电磁波发射到接收过程中,角度$θ$没有发生变化,发射有一个$F_电(θ)$,接收再乘以一个$F_电(θ)$,所以有一个平方项
根据余弦定理有:
近似可得:
将$\theta$带入U:
将上式在$\delta$处展开为泰勒级数并忽略高次项,有:
- $U_0=KF_电^2(\delta)$
- $\eta=\frac{-2F_电’(\delta)}{F(\delta)}$
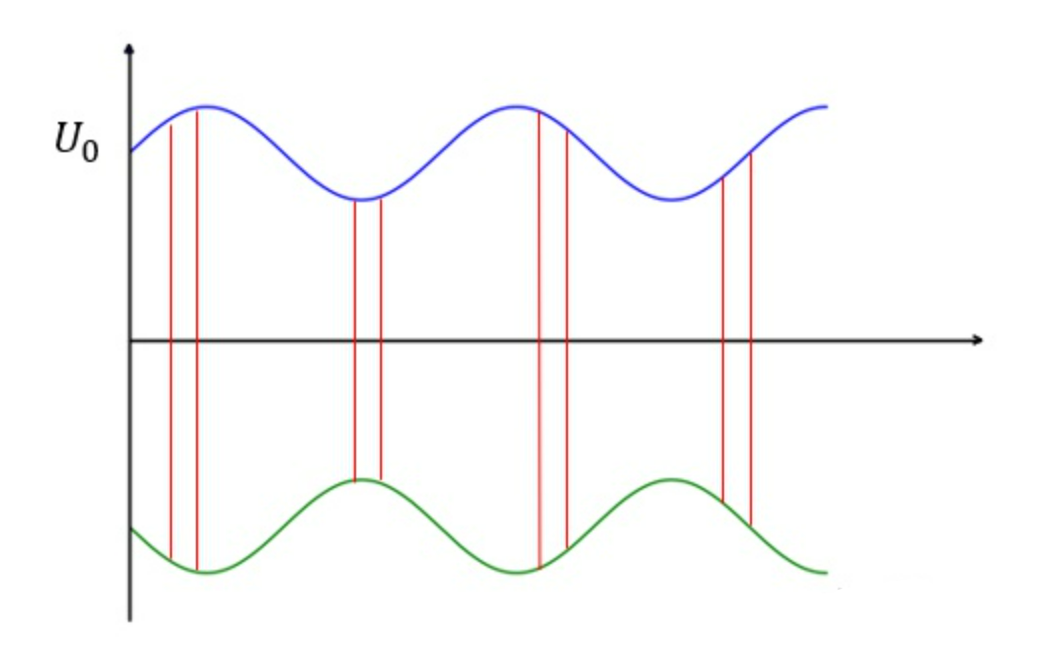
$U$反映的是回波信号的幅度,且随着时间 t 在发生变化。当$ϵ=0$的时候,$U$为一常数,说明此时目标就在旋转轴上,为一等幅信号。$\epsilon\neq0$的时候,$U$为一调幅信号
取出回波信号的包络,消除直流分量,则可以测得信号的包络为$U_0\eta\epsilon cos(w_st-\phi_0)$
真正进行角度跟踪,光知道$ϵ$并不能唯一确定目标位置。需要知道方位和俯仰误差两部分,即$U_0\eta\epsilon cos(\phi_0)、U_0\eta\epsilon sin(\phi_0)$
- 误差电压分解的办法是采用两个相位鉴别器,相位鉴别器的基准电压分别为$cos(ω_st)$和$sin(ω_st)$
- 将这两项分别与前面的包络项相混频(相乘),然后过低通滤波器,就可以得到方位和俯仰误差两部分分量
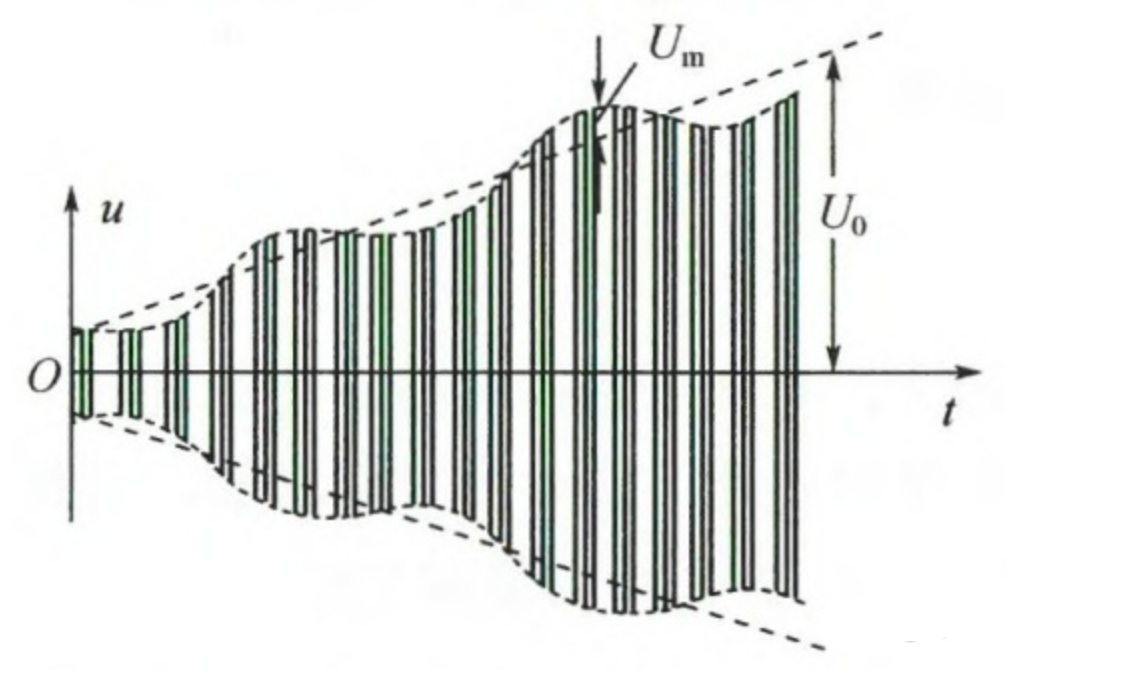
前面的推导是假设$U_0$为一常数,即$K$为常数,也就是说假设目标是静止不动的。如果目标远离雷达或者向着雷达运动,$K$就会发生变化,不再是一个常数。如果目标向着雷达运动,$K$就会逐渐变大
2.单脉冲自动测角系统
在一个角平面内,两个相同的波束部分重叠,其交叠方向即为等信号轴。将两个波束同时接收到的回波信号振幅进行比较,即可取得目标在该平面上的角误差信号,然后将此误差信号电压放大变换后加到驱动电机,控制天线向减小误差的方向运动
和差比较器是单脉冲雷达的重要部件,由它完成和、差处理,形成和差波束。用得较多的是双T接头
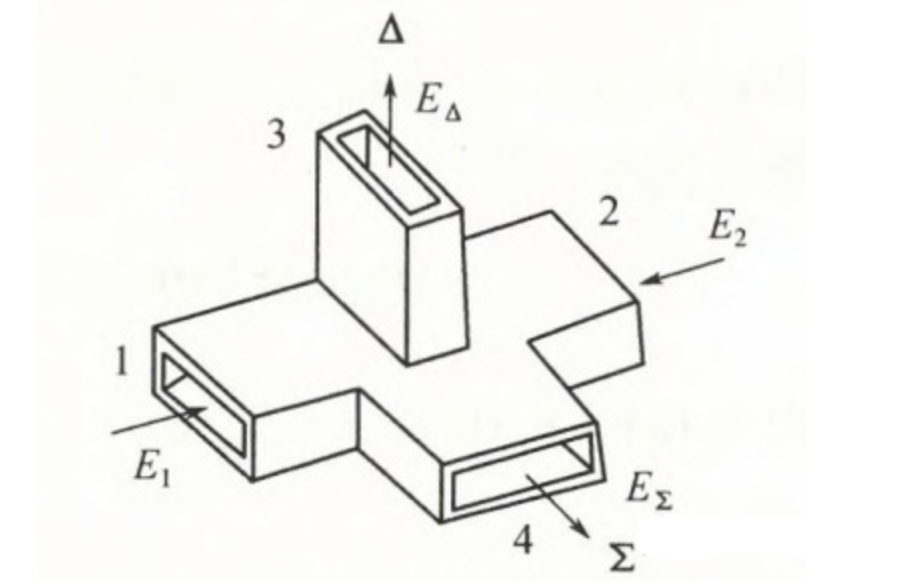
2.1 雷达发射过程
发射时,从发射机来的信号加到和差比较器的$Σ$端,$Δ$端无输出,$1,2$两端输出同幅同相信号
两个馈源被同相激励并辐射相同的功率,结果两波束在空间各点产生的场强同相相加,形成发射和波束$F_Σ(θ)$[以下都是电压天线图]
2.2 雷达接收过程
双 T 接头的$1,2$端输入,$Δ$端输出差信号,$Σ$端输出和信号。到达$1,2$的回波信号为$K_FΣ(θ)$,振幅用$K$表示
2.3 理论分析
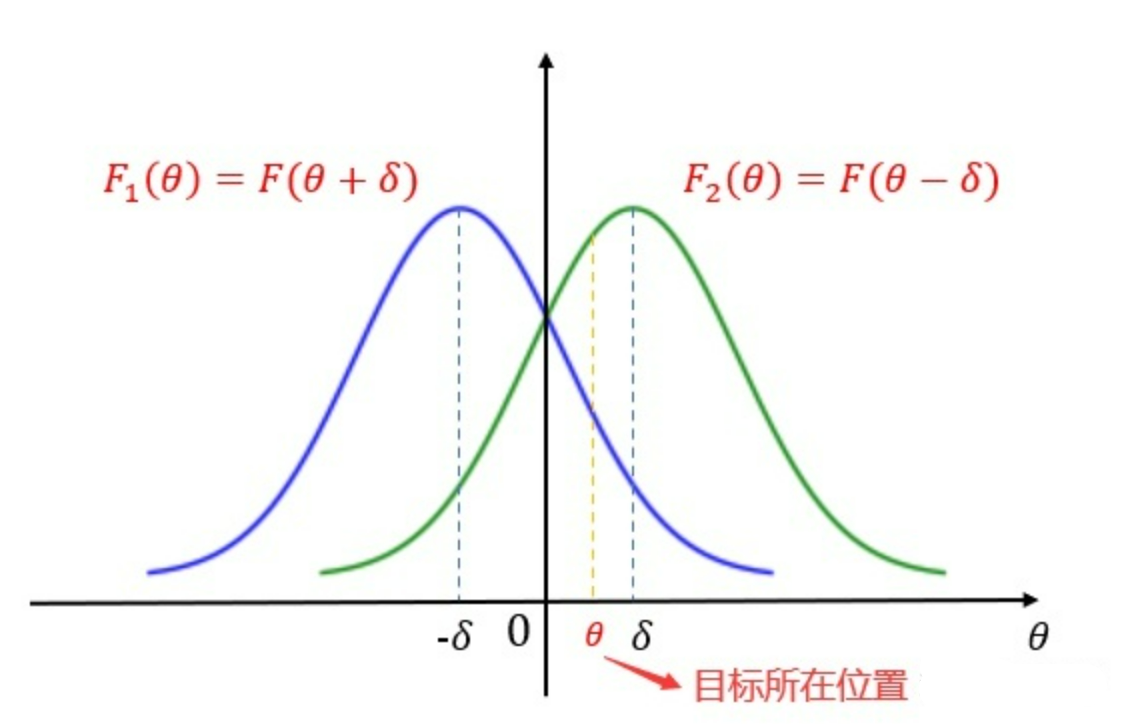
雷达通过和天线方向图将信号发射出去,接收时,得到$Δ$和$Σ$信号,需通过$Δ$和$Σ$将目标所在位置$θ$求出来,就达到了自动测角的目的
将$F(\theta+\delta)$与$F(\theta-\delta)$在$\delta$处做泰勒展开,忽略高阶项得到:
将$F(θ±δ) 、 F_Σ 、 F_Δ$带入到$Σ$和$Δ$的表达式中,得到:
式中,$Σ 、 Δ 、 δ 、 F$函数均为已知项,$K$和$θ$为未知项,将两式相比得到:
最终得到$\theta$:
只要收到一个脉冲,就能输出$Σ$信号和$Δ$信号,将两者相比就能得到$θ$
- $Σ$和$Δ$同相,$θ$就为正;
- $Σ$和$Δ$反相,$θ$就为负。
