本节主要介绍了雷达目标距离测量的两种方式:脉冲法与调频法。
脉冲法测距
1.基本原理
目标到雷达的距离的计算公式为$R=\frac{1}{2}Ct_R$,时间$t_R$就是回波相对于发射信号的延迟,因此,目标距离测量就是要精确测量延迟时间$t_R$
有两种定义回波到达时间$t_R$的方法:一种是以目标回波脉冲的前沿作为它的到达时刻;另一种是以回波脉冲的中心(或最大值) 作为它的到达时刻
回波脉冲中心估计
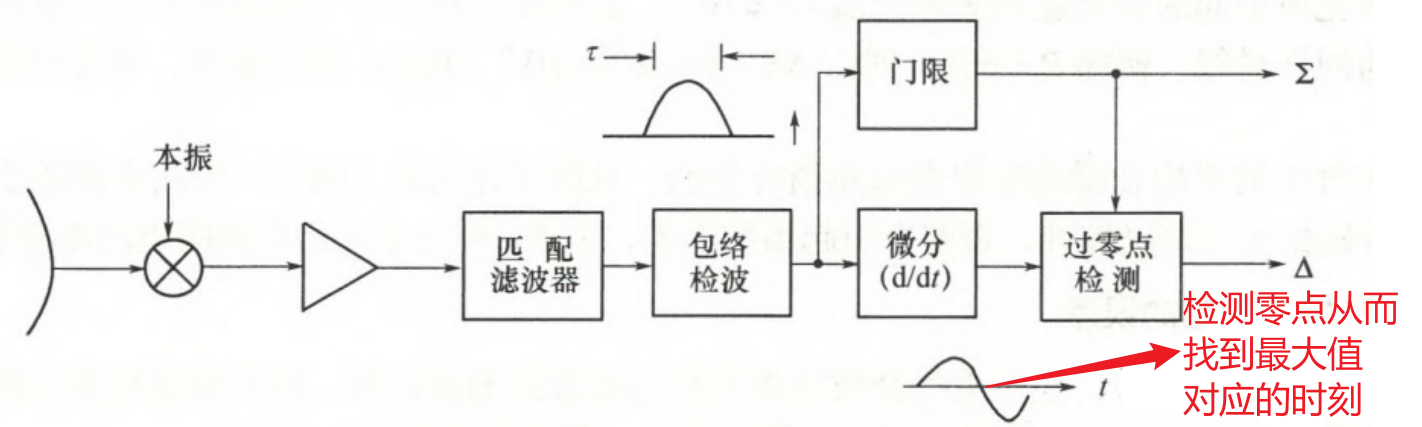
2.影响测距精度的因素
$\because R=\frac{1}{2}Ct_R,\therefore dR=\frac12Cdt_R+\frac12t_RdC=\frac12Cdt_R+\frac RCdC$
时间差的影响:$d{t_R}\downarrow,d{R}\downarrow$
- 传播速度变化的影响:$\frac{dR}R\propto \frac{dC}C$
- 大气折射的影响
- 测读方法误差
3.距离分辨率
距离分辨率$\Delta R$是指同一方向上两个大小相等点目标之间的最小可区分距离
通常希望距离分辨率$\Delta R$越小越好,但$\Delta R\downarrow,\Rightarrow\tau\downarrow,\Rightarrow R_{max}\downarrow$,故存在距离分辨力和最大作用距离的矛盾问题
解决上述问题的办法:发射脉冲压缩波形,比如线性调频信号,接收时对回波进行匹配滤波
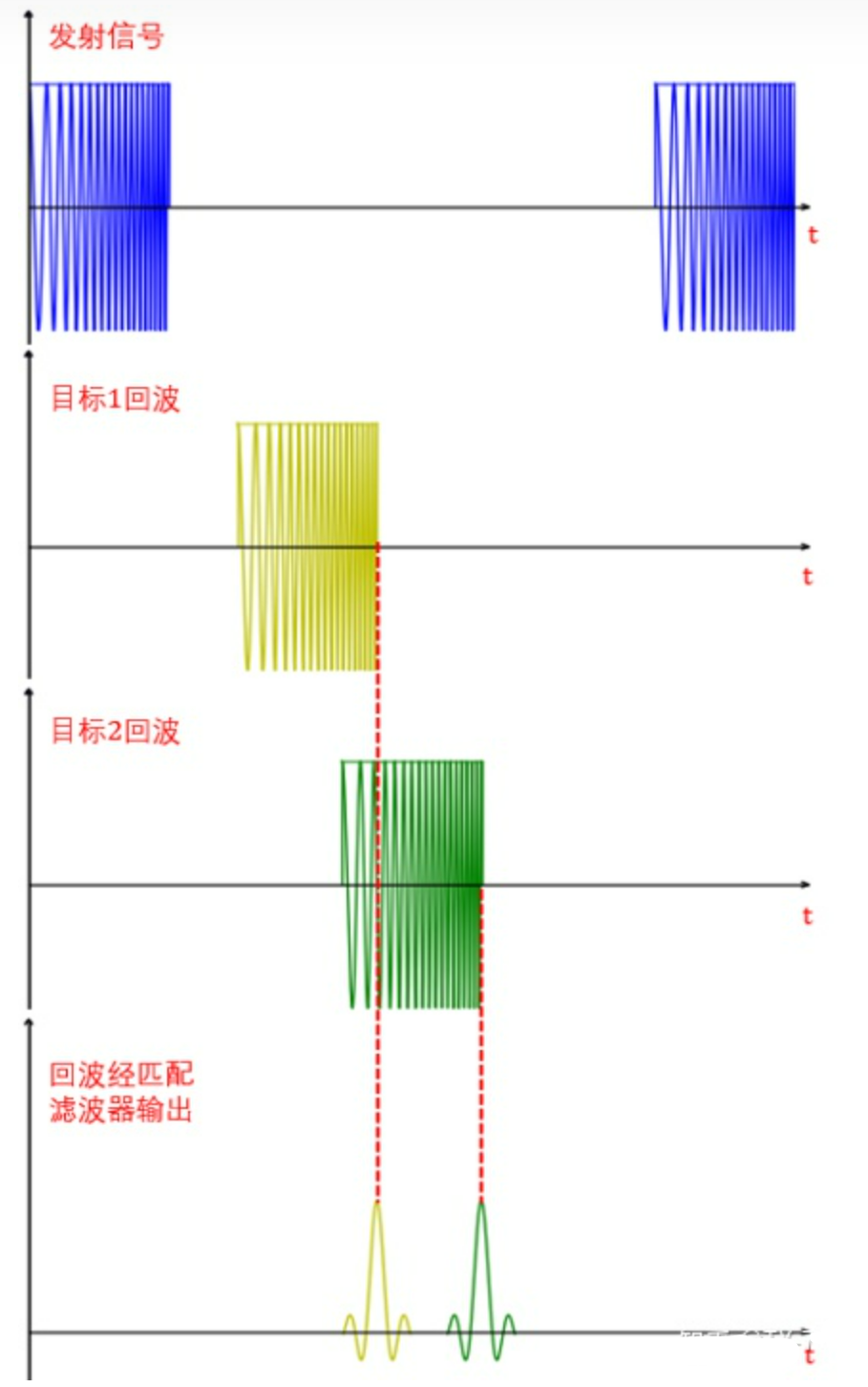
- 采用-4dB的点的宽度来表示辛克函数的宽度,此时对应的时间为$\frac1B$
- 则脉压雷达的距离分辨率为:$\Delta R=\frac12C\cdot\frac1B$
- 线性调频信号的带宽:$B=\mu\tau$
- 故线性调频信号经过匹配滤波器后距离分辨率为:$\Delta R=\frac C{2\mu\tau}$
- 对于普通雷达,$τ$增大,$ΔR$增大; 对于线性调频信号,$τ$增大,$ΔR$减小
- 匹配滤波对于普通雷达而言,可以达到输出信噪比最大的作用;对于脉压雷达,还可以提高距离分辨力
4.最大无模糊测距范围
最小测距范围:$R_{min}=\frac12C(\tau+t_0),其中t_0为收发开关的转换时间$
最大无模糊作用距离:$R_{max}=\frac12CT_r$,其出现原因是最大距离大于脉冲重复周期$T_r$,不能确定距离跨越了几个$T_r$周期
雷达探测目标,首先应该考虑达到最大作用距离,这时$T_r$就确定下来了。再来考虑是否满足最大无模糊距离。如果不满足,就需要解模糊
$R$:目标到雷达的距离
$m$:假设跨了$m$个周期
$t_r$:回波离它最近主波之间的时间差
5.距离模糊的判决方法(重频参差(两重频))
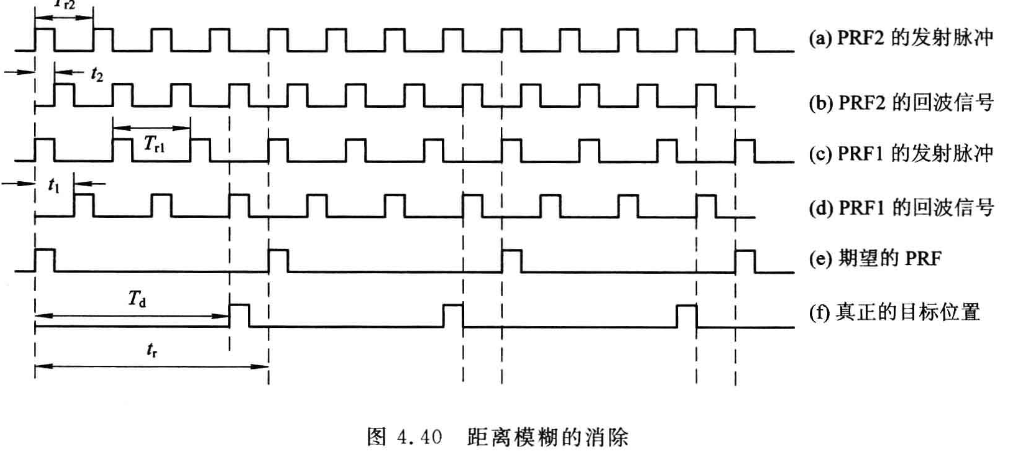
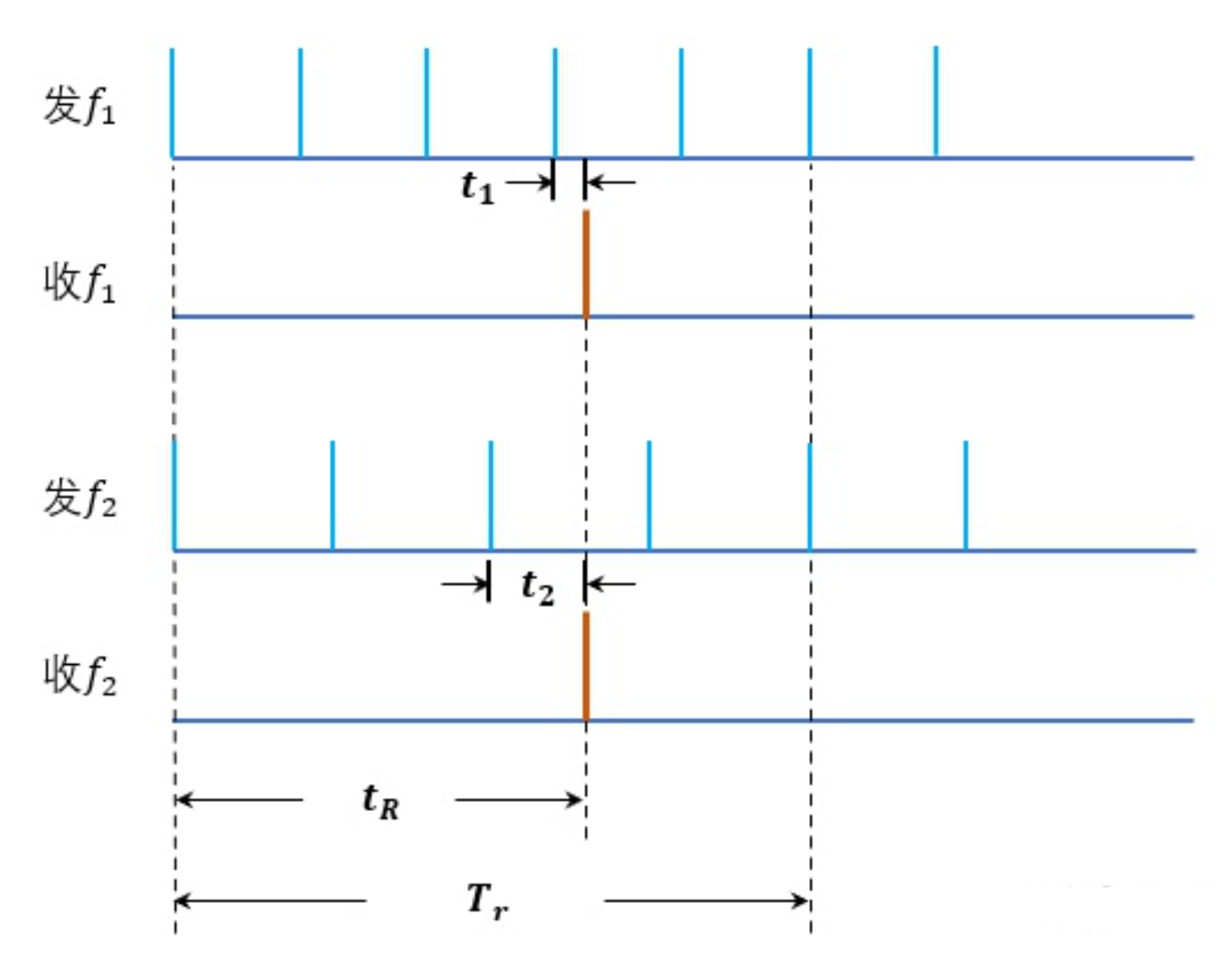
$t_1,t_2$是发射脉冲1和发射脉冲2接收到的回波与最近的发射脉冲之间的时间差,应满足如下条件:
- 两种PRF下发射的脉冲数目互斥,如选取:$f_{r1} = N\cdot f_{rd}、f_{r2}=(N+1)\cdot f_{rd}$
- 在一个期望的脉冲重复周期(PRI)内,两种发射信号的回波仅在一个时延位置上重合,这就是真正的目标位置
设$n_1,n_2$为两组发射脉冲的跨周期数
则当两发射信号的回波在同一个时刻重合时,有:
两种发射信号的回波仅在一个时延位置上重合,这就是真正的目标位置(因为目标与雷达之间的距离是确定的,无论脉冲重复频率怎么变,同一时间发出的脉冲,回波到达雷达的时间是相等的)
$f_{r1},f_{r2}$可以看成一个基础频率$f_r$上的倍频,有:
通常取$a=1$(图中$N=4$),则有:
当$a=1$时,$n_1,n_2$的关系有两种可能,即$n_1=n_2$和$n_1=n_2+1$:
当$n_1=n_2(t_1>t_2)$时,可得:
当$n_1=n_2+1(t_1<t_2)$时,可得:
重频参差的最大模糊距离:
重频参差并没有消除距离模糊的问题,而是将最大模糊距离扩大了
调频法测距(三角形波调制测距)
发射频率按周期性三角波形的规律变化:
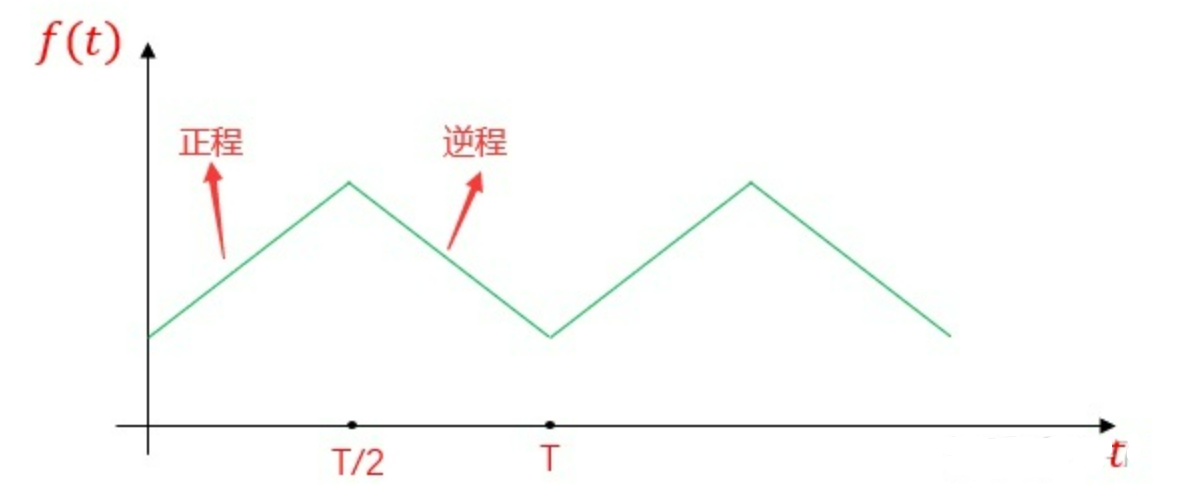
正程:
发射频率:$f(t)=f_0+\mu t$,其对应的发射信号的时域表达式为:$S_t(t)=Acos(2\pi f_0t+\pi\mu t^2)$
则接收信号的时域表示:
- $v_t$:目标相对于雷达的径向速度
- $R_0$:目标到雷达的初始距离
$S_r(t)$对时间求导,可以得到接收信号的频率$f_r$:
- 由于多普勒频率$f_d=\frac{2v_t}{\lambda}$,$C>>v$
- 则:
逆程:
发射频率:$f_t=f_0-\mu t$
与正程推理相同,则可得到接收频率$f_r$:
则物体无运动,忽略$f_d$,有:
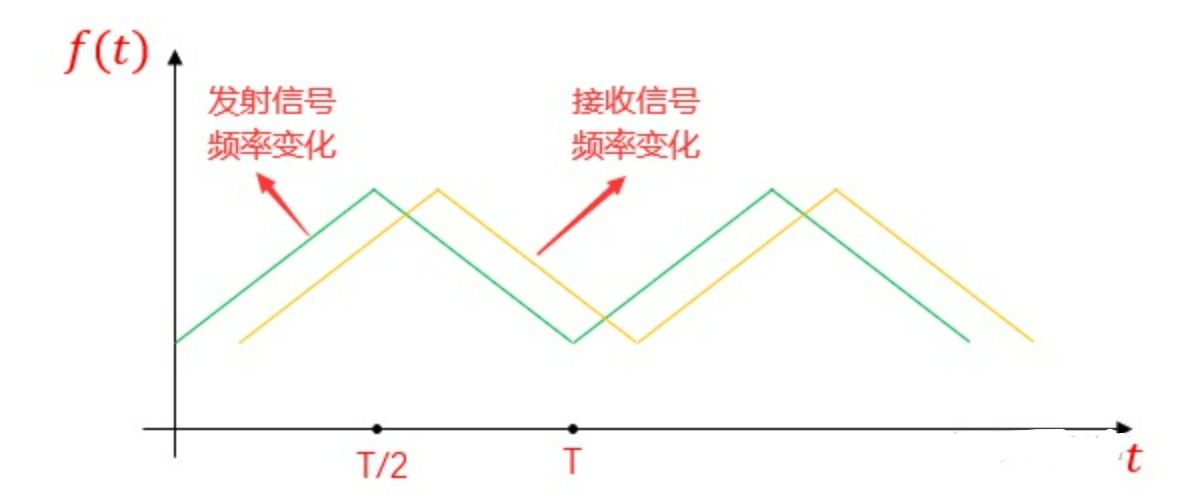
求差频的平均值:
正程频率差$f_{b^+}$:
负程频率差$f_{b^-}$:
频率计测得的差频的平均值$F_{bav}$:
则:
