本节主要介绍了雷达接收机的任务与组成、重点描述了雷达接收机的高频部分与中频部分。
雷达接收机的任务
- 不失真地放大所需的微弱信号，抑制不需要的其他信号
- 其他信号包括：
- 噪声（noise）：无意的；
- 干扰（jamming）：一般认为是有意的；
- 杂波（clutter）：近地物，如山川、海浪的回波。
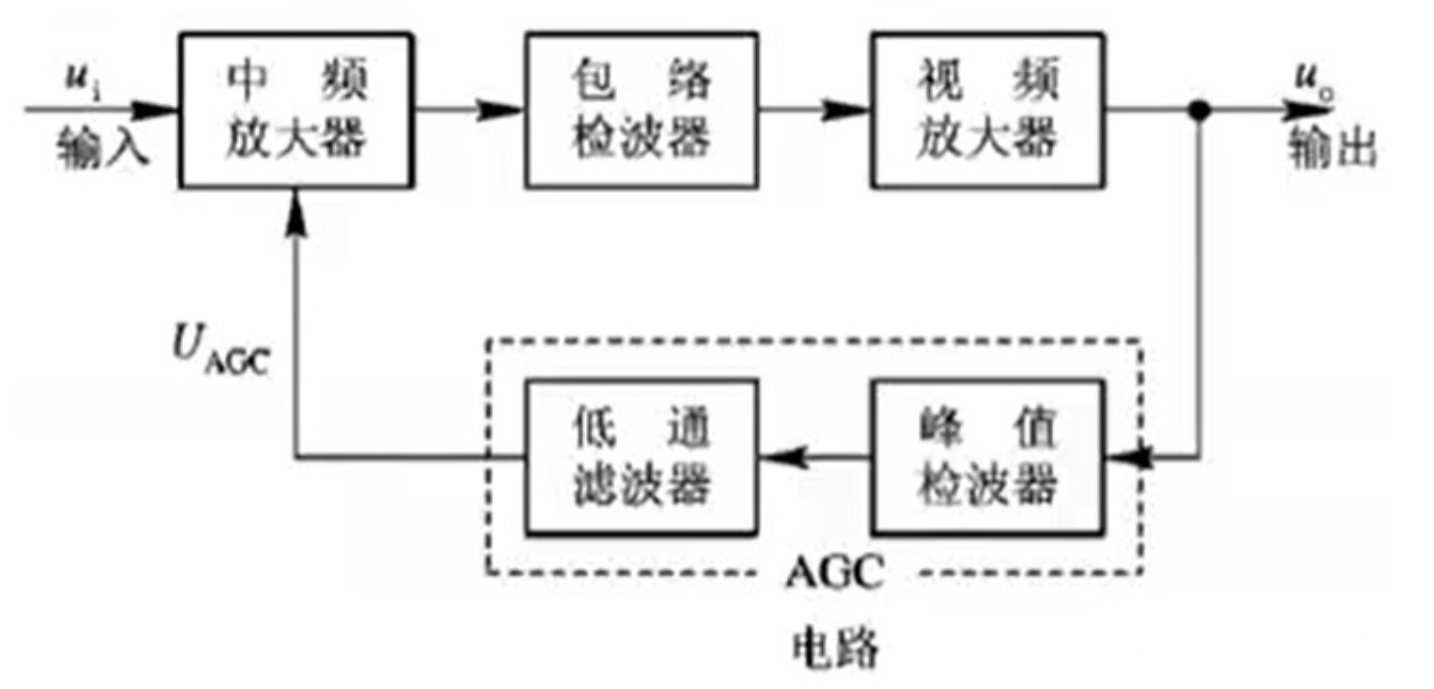
超外差雷达接收机组成
- 高频部分：
- T/R：收发转换开关，存在于收发天线共用的系统中
- 接收机保护器：超过接收机最大功率，进行强制限流，以免对接收机造成损坏
- 低噪声高频高增益放大器
- 混频器及本振：实现下变频，将信号频率变为中频
- 中频部分：
- 中频放大器：主要通过匹配滤波器实现，提高输出SNR
- AGC：Automatc Gain Control， 自动增益控制
- 视频部分：
- 包络检波
- 放大
接收机的噪声系数和灵敏度
1.接收机中的噪声
噪声来源：
电阻热噪声 天线噪声 谱性质 高斯白噪声：（-∞~+∞内功率谱密度恒定） 高斯色噪声（在某一较大频带内功率谱密度恒定） 噪声电压均方值（反映的是功率） $\bar{U_n^2}=4kTB_nR$ $\bar{U_n^2}=4kT_BB_nR_A$ - k为玻尔兹曼常数，$k = 1.38\times 10^{-23}$
- T为电阻的热力学温度，以绝对温度（K）计量，对于$17^oC$的室温，$T = T_0 = 290K$，称为标准噪声温度
- R为电阻的阻值
- $B_n$为测试设备的通带，在这里就是接收机的带宽
- $R_A$为天线等效电阻
定量描述噪声信号：
等效噪声功率谱宽度或噪声带宽
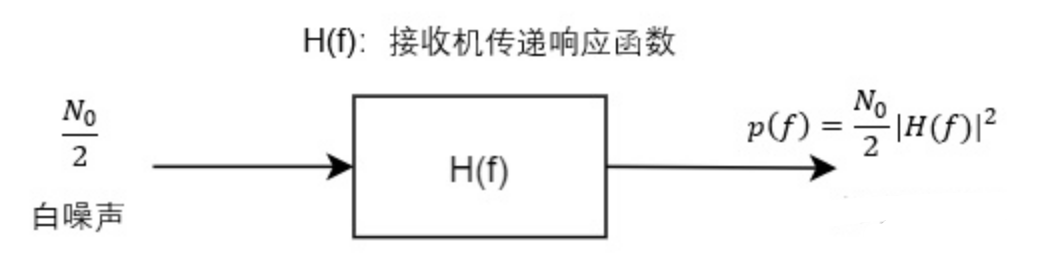
功率谱均匀的白噪声，通过具有频率选择性的接收线性系统后，接收机输出的白噪声功率谱密度如下：
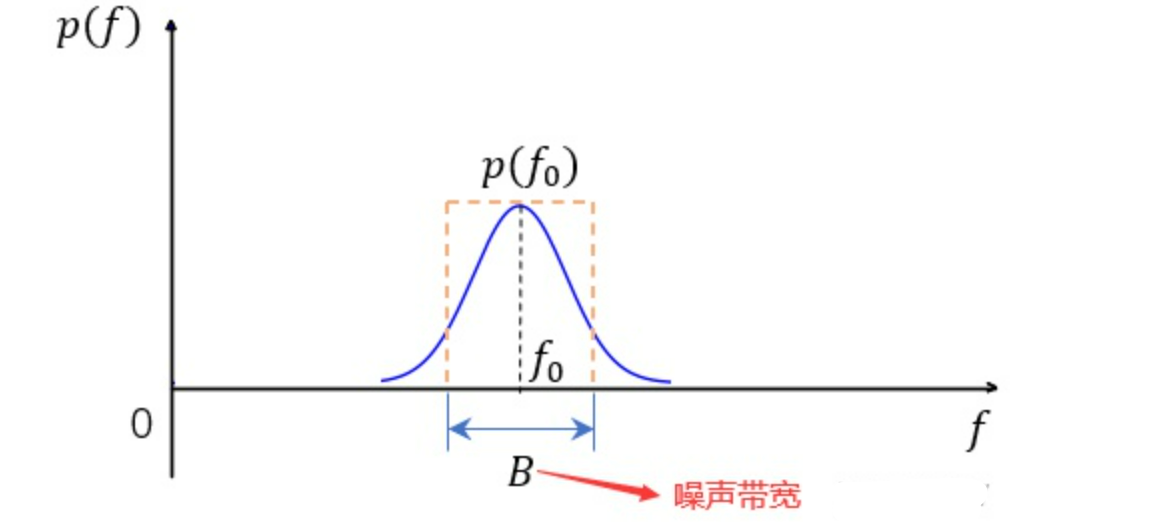
则为了分析和计算方便，通常把这个不均匀的噪声功率谱等效为在一定带宽B内是均匀的功率谱。这个带宽B称为等效噪声功率谱宽度，一般简称噪声带宽。
功率谱在频率轴上进行积分就得到噪声功率，假设其与噪声带宽内的功率相等，即可求得$B=\frac{\int_{0}^{\infty}{p(f)}df}{p(f_0)}=\frac{\int_{0}^{\infty}{|H(f)|^2}df}{H(f_0)}$
从上述公式可知，噪声带宽是受|H(f)|限制的，|H(f)|反映的是雷达接收机中频滤波器的传递响应函数。接收机中频滤波器又是根据 $h(t)=KS^(t_0−t)$ 来设计的，$S(t)$表示雷达信号。也就是说*信号本身的带宽就决定了中频滤波器怎么设计。因此，我们可以认为信号带宽、接收机带宽、噪声带宽是近似相等的**。
2.噪声系数
噪声系数是指接收机输入端信噪比$SNR_i$与输出端信噪比$SNR_o$的比值
它的物理意义是指由于接收机内部噪声的影响，使接收机输出端的信噪比相对于其输入端的信噪比变坏的倍数，噪声系数可表示为：
$$
F = \frac{(SNR)_i}{(SNR)_o}=\frac{\frac{S_i}{N_i}}{\frac{S_o}{N_o}}=\frac{N_o}{N_iG_a}
$$- 其中：$N_i = kT_0B$为输入噪声功率，$G_a$为接收机的额定功率增益，$G_a = \frac{S_o}{S_i}$
假设接收机内部噪声的额定功率为$\Delta N$，输出噪声功率为：
$$
N_o = N_iG_a+\Delta N = kT_0B_nG_a+\Delta N
$$合并上述两式可得到噪声系数F为：
$$
F = 1+\frac{\Delta N}{kT_0B_nG_a}\ge 1
$$若有n级电路级联，则n级电路级联时的总噪声系数为：
$$
F_o = F_1 + \frac{F_2 - 1}{G_1}+\frac{F_3 - 1}{G_1G_2}+…+\frac{F_n-1}{G_1G_2…G_{n-1}}
$$
3.灵敏度
接收机灵敏度表示接收机接收微弱信号的能力
能接收的信号越微弱，则接收机的灵敏度越高，因而雷达的作用距离就越远
灵敏度用接收机输入端的最小可检测信号功率$S_{imin}$来表示，其表达式为：
$$
S_{imin}=N_iF(\frac{S_o}{N_o}) = kT_0BF(\frac{S_o}{N_o})
$$为了保证检测系统发现目标的性能，要求$(\frac{S_o}{N_o})\ge(\frac{S_i}{N_i}){min}$，接收机实际灵敏度为：
$$
S{imin}= kT_0BF(\frac{S_o}{N_o})_{min} = kT_0BFM
$$其中，$F$为噪声系数，其定义为接收机输入端信号噪声比与输出端信号噪声比的比值，即$F=\frac{S_i/N_i}{S_o/N_o}$
M为识别系数，定义接收机输出端信噪比的最小值$M=(\frac{S_o}{N_o})_{min}$，即达到一定检测性能所要求的接收机输出信号的最小信噪比
雷达接收机的高频部分
1.高频组成部分
- 收发转换开关、接收机保护器、低噪声高频高增益放大器、混频器、本机振荡器
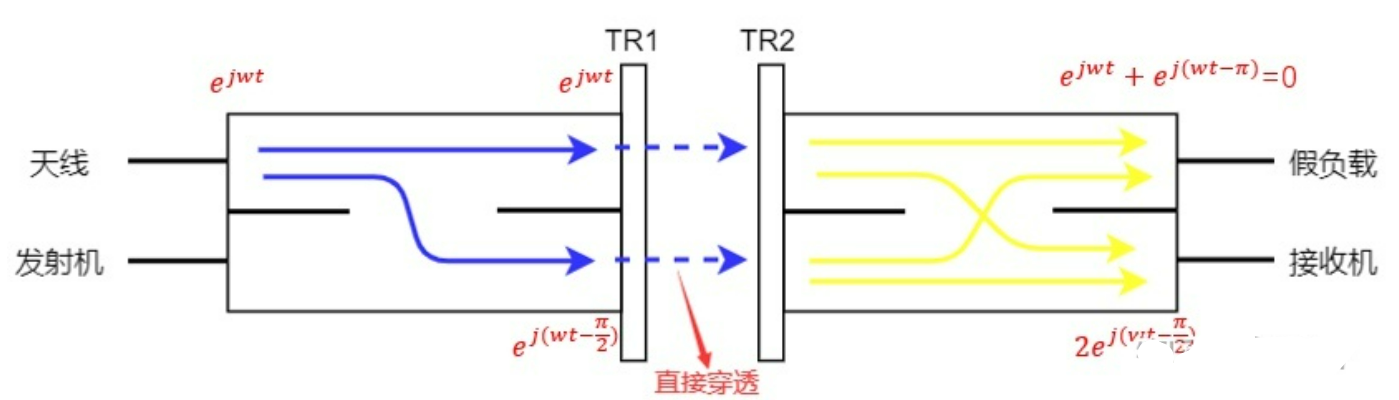
2.平衡收发转换开关
发射状态时：
- 保护放电管 TR1、TR2 放电，大部分能量被反射（图中蓝色虚线），
- 只有一部分漏过放电管（图中黄线），在接收机处反向相消。
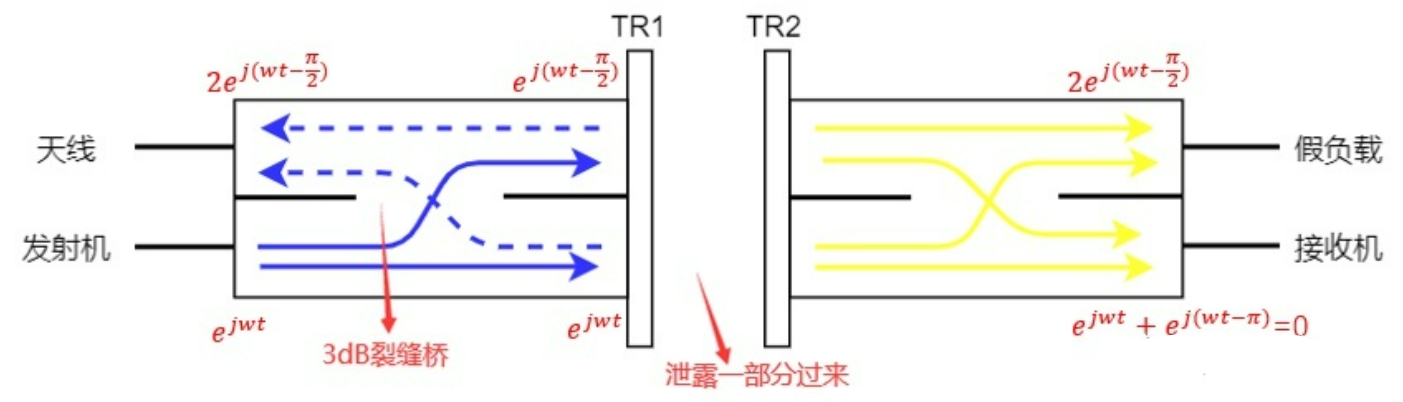
接收状态时：
- 保护放电管 TR1、TR2 不放电，天线接收到的信号在接收机处同相相加
- 就算有少数信号穿过，在假负载处也会相互抵消
3.本机振荡器（LO）和自动频率控制（AFC）
3.1 混频器原理
超外差式接收机利用本机振荡器和混频器把高频回波信号变换成便于滤波和处理的中频信号
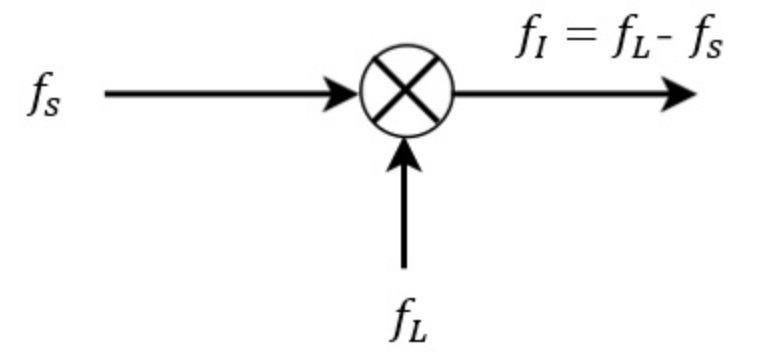
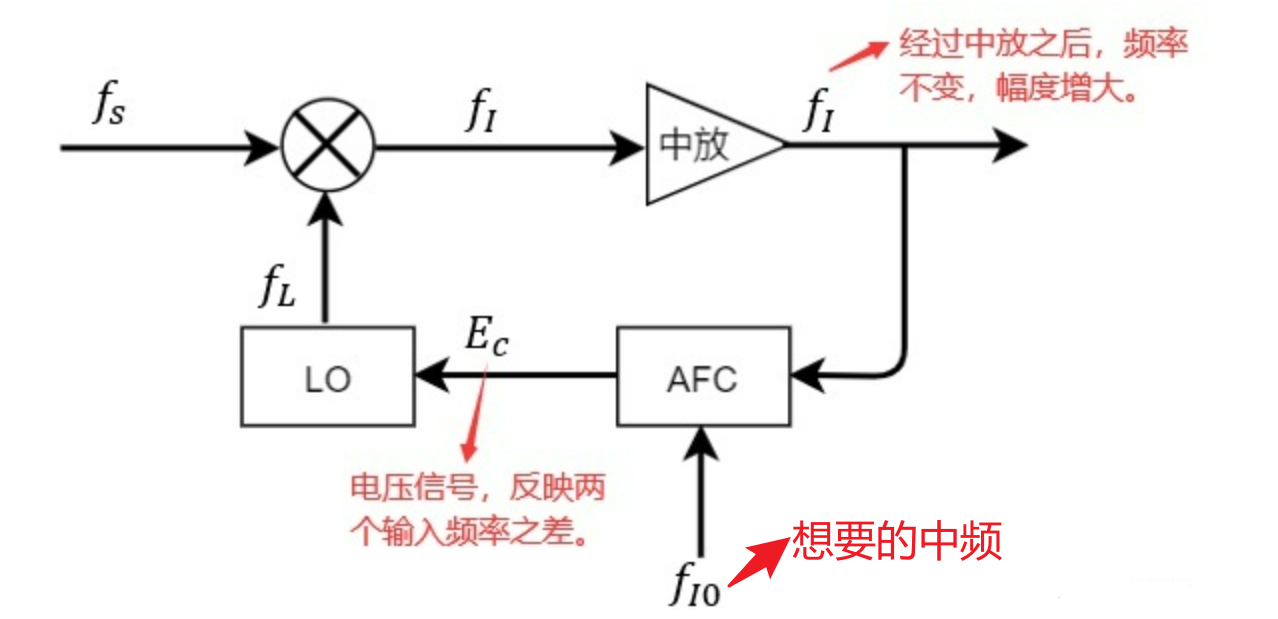
理想情况下，发射的高频信号$f_R$和本振频率$f_L$都是固定的，混频后二者之差也是固定不变的 “ 正确中频 ”$f_I$。但在实际工作中，常规雷达发射机磁控管振荡器和接收机本机振荡器频率稳定度不高，容易受外界条件（温度、负载、电源等）的改变而变化，使混频后的实际中频偏离 “ 正确中频 ”$f_I$。可能超出中放通带，使接收机增益大大降低甚至不能正常工作。因此，必须采用AFC，以保证混频器输出为 “ 正确中频 ” $f_I$。
3.2 常规雷达本振与AFC
接收机的动态范围
接收机的动态范围表示接收机能够正常工作所容许的输入信号强度变化的范围
信号太弱，它不能检测出来；信号太强，接收机会发生饱和而失去放大作用，这种现象称为过载
使接收机开始出现过载时的输入功率与最小可检测功率之比，叫做动态范围，其公式为：
$$
D(dB)=10lg\frac{P_{imax}}{P_{imin}}=20lg\frac{U_{imax}}{U_{imin}}
$$- D表示接收机的动态范围，单位 dB
- $P_{imax}$ 表示最大接收信号功率
- $P_{imin}$ 表示最小接收信号功率，即灵敏度
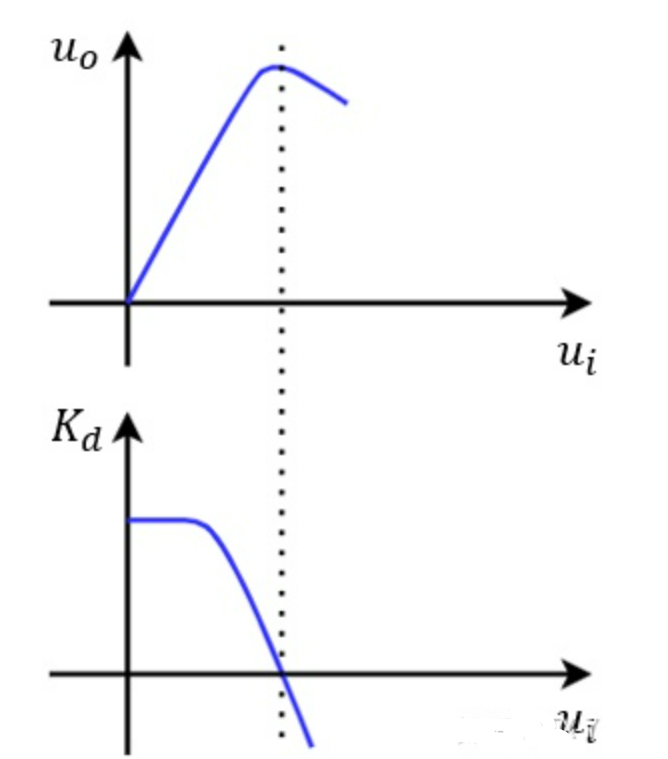
饱和过载：
- 定义增量增益$K_d=\frac{du_o}{du_i}$，若$K_d\le0$，则称为饱和过载
滤波与接收机带宽
1.中频放大器（匹配滤波器）
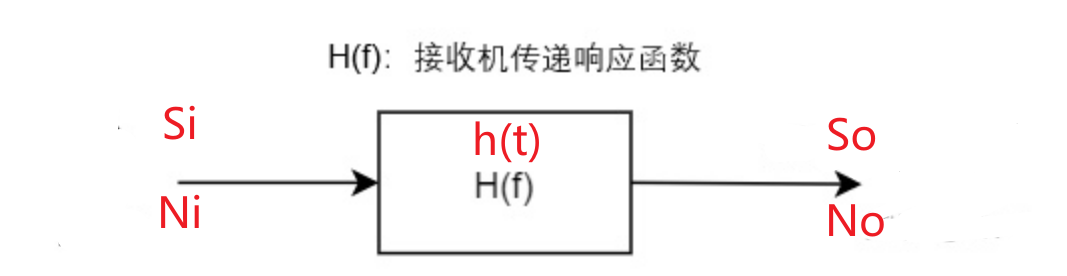
匹配滤波器是当输入端出现信号与加性白噪声时，使其输出信噪比最大的滤波器，就是一个与输入信号相匹配的最佳滤波器
冲击函数$h(t)$：
$$
h(t)=KS^*(t_0-t)
$$- 说明匹配滤波器实际上是根据雷达发射信号$S(t)$设计的。
- 输出信噪比在$t_0$时刻达到最大。
传递响应函数$H(f)$：
$$
H(f)=KS^*(f)e^{-j2\pi ft_0}=|H(f)|e^{j\phi(f)}
$$匹配滤波器的最大输出信噪比：
$$
(\frac{S}{N})_{omax}=\frac{E}{N_o/2}
$$- 其中，$N_0/2$为白噪声功率谱密度。
- $E$为输入信号能量，根据帕塞瓦尔定理：$E=\int_{-\infty}^{+\infty}|S(t)|^2dt=\int_{-\infty}^{+\infty}|S(f)|^2df$
- 由此可知，匹配滤波器输出端的峰值瞬时信号功率与噪声的平均功率之比$SNR_o$等于两倍的输入信号能量除以输入噪声功率
- 也就是说，匹配滤波器输出最大信噪比仅依赖于信号能量和输入噪声功率，而与雷达使用的波形无关
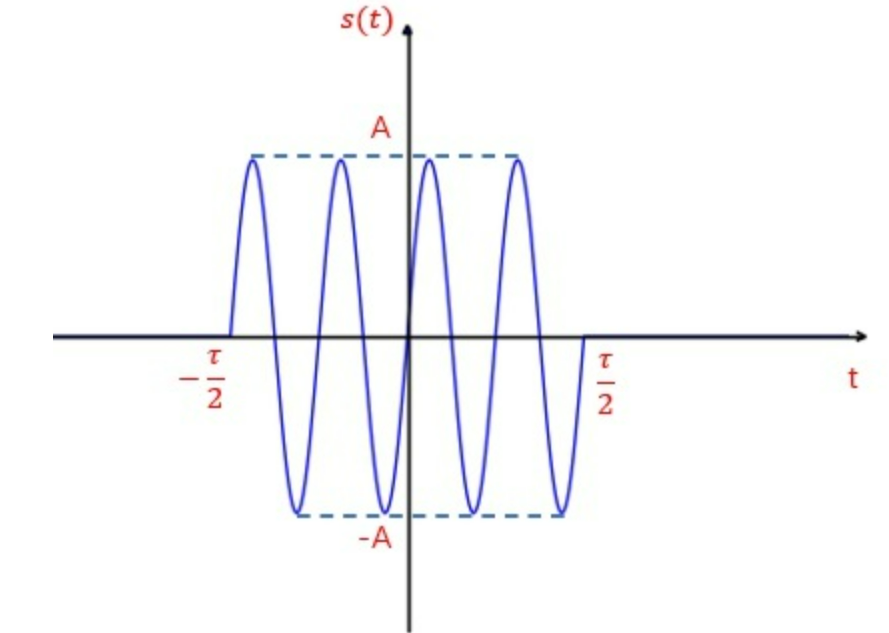
2.单个脉冲信号的匹配滤波
假设矩形脉冲幅度为A，脉宽为$\tau$，信号波形为：
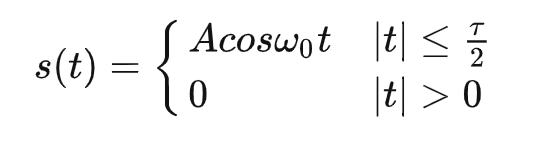
经傅里叶变换，可得信号频谱：
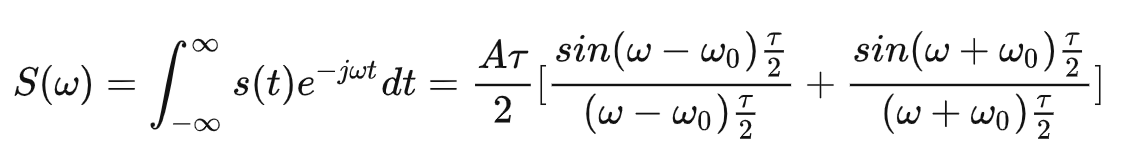
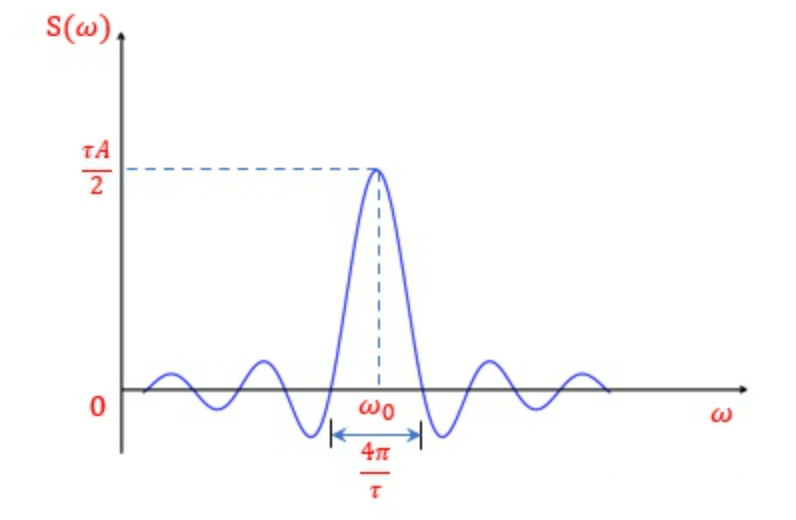
此时，匹配滤波器的带宽为$B\approx\frac{1}{\tau}$
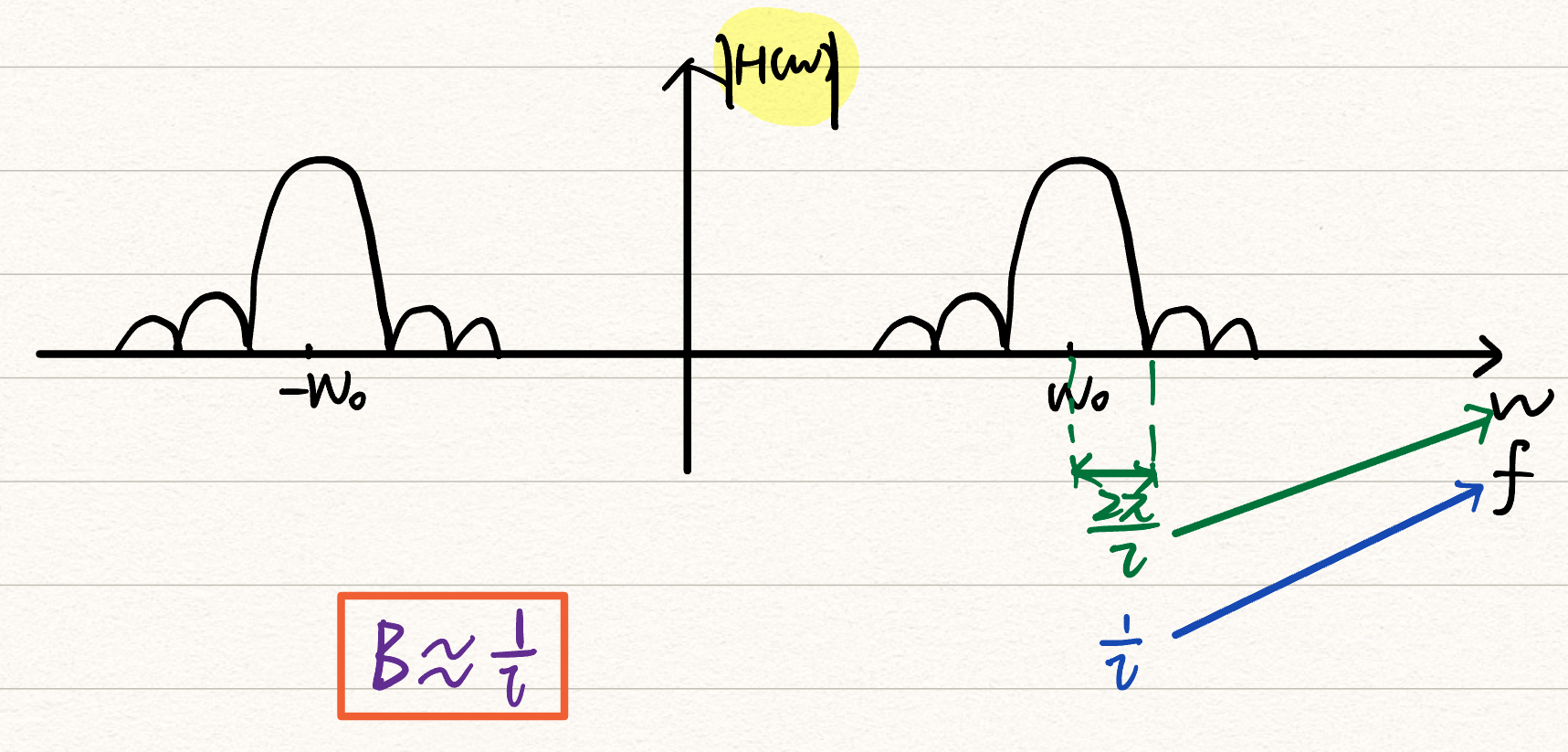
3.准匹配滤波
理想匹配滤波器的特性一般比较难以实现，因此，需要考虑它的近似实现，即采用准匹配滤波器。
准匹配滤波器是指实际上容易实现的几种典型频率特性。通常可以用矩形、高斯型或其他形状的频率特性来作近似
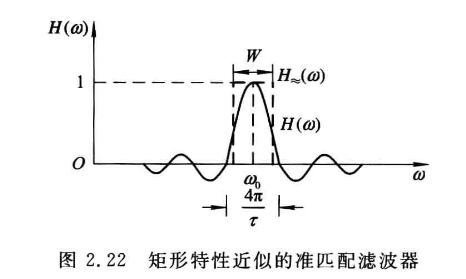
- 其中实线为理想的匹配滤波器的频率特性，虚线为矩形特性滤波器的频率特性
准匹配滤波器的最大输出信噪比与理想匹配滤波器的最大输出信噪比的比值定义为失配损失ρ：
$$
\rho=\frac{(\frac{S}{N})_{\approx max}}{\frac{E}{N_o/2}}\le1
$$
- 准匹配滤波器的最大信噪比$(\frac{S}{N})_{\approx max}$
- 理想匹配滤波器输出的最大信噪比$(\frac{S}{N})_{omax} = \frac{E}{N_o/2}$
增益控制
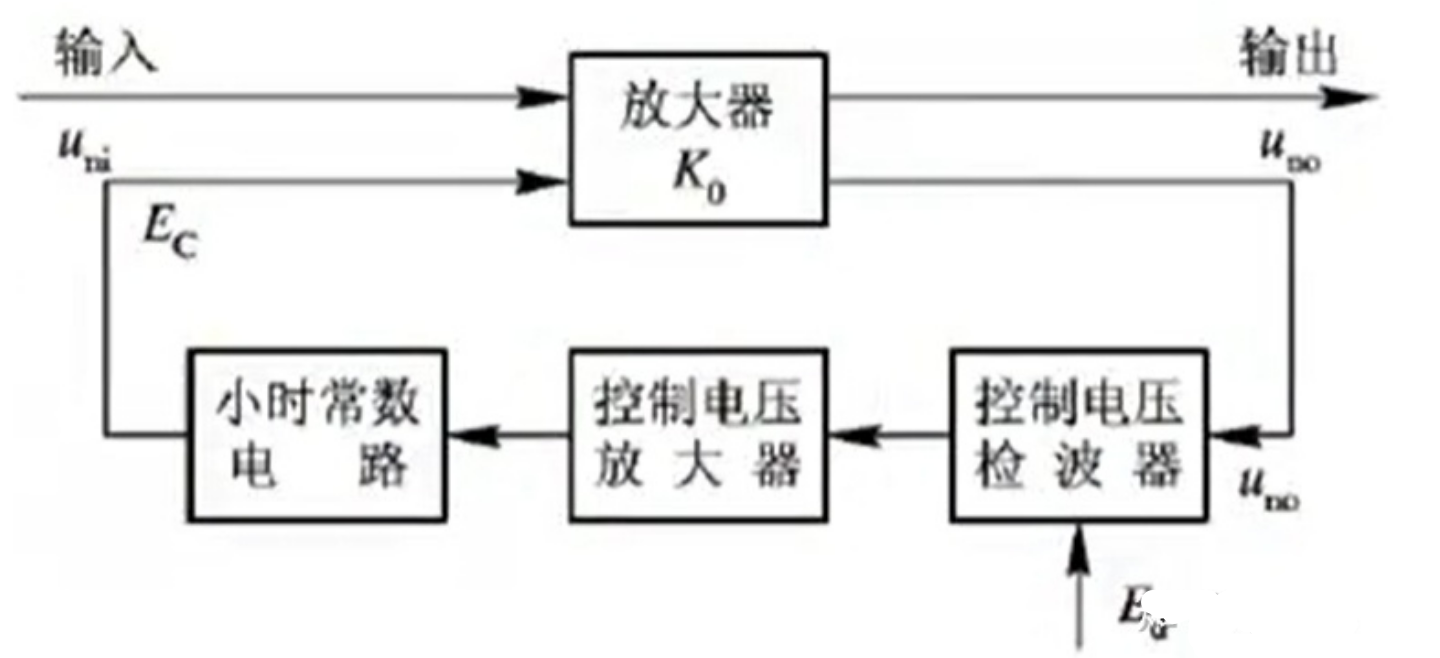
自动增益控制（AGC）
- 目的是为了使接收机的输出不要受接收机输入影响太大，引起剧烈变化
- 从视频取反馈控制信号，最终控制中频放大器的增益
- AGC是负反馈系统
瞬时自动增益控制（IAGC）
- 目的是使大功率干扰受到衰减，而维持目标信号的增益尽量不变。
- 直接从中频放大器的输出端取反馈控制信号。因此，IAGC比AGC反应更快。
