雷达原理之雷达作用距离

本节主要介绍了雷达作用距离的影响因素，包括最小可检测信号、脉冲积累、目标截面积、系统损耗等，以及不同形式的雷达方程。

雷达方程

1.基本雷达方程

• 雷达基本方程，也叫做最大作用距离方程

  

• $P_t$：雷达发射机发射信号的功率

• $G_t$：发射天线增益，这里假设目标与雷达天线的连线正好穿过天线方向图最大增益处

• $G_r$：接收天线增益，若天线为收发共用，有$G_r$=$G_t$

• $\sigma$：表示目标的雷达截面积（RCS），其反映入射电磁波照射到目标上之后发射回来的电磁波的大小。隐身飞机就是将 σ 做的很小。当雷达电磁波照射到目标上之后，反射回来的电磁波功率很弱，就达到了目标对雷达隐身的目的。

• $S_{imin}$表示接收手机灵敏度，即最小可检测信号

• 假设电磁波反射回来之后，经过接收天线主瓣最大值（接收天线方向图最大增益为$G_r$），接收机接收到的信号功率就等于反射回来的信号功率乘以接收天线的有效面积$A_r$。此时，接收机能否检测到信号跟$S_{imin}$有关。

• 如果满足，$P_r≥S_{imin}$，雷达就可以探测到目标

2.方程公式推导

• 到达目标的入射功率密度为:
  $$
  \frac{P_tG_t}{4\pi R^2}
  $$

• 目标反射回来的功率为：
  $$
  \frac{P_tG_t\sigma}{4\pi R^2}
  $$

• 假设接收天线的有效面积为$A_r$：
  $$
  \frac{P_tG_t\sigma}{4\pi R^2}\times\frac{A_r}{4\pi R^2}
  $$

• 由于$A_r$与$G_r$的关系为：
  $$
  G_r=\frac{4\pi A_r}{\lambda^2}
  $$

• 故最终接收到的功率为：
  $$
  P_r=\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3R^4}
  $$

• 而当$P_r$=$S_{simin}$时，R就取得最大值：
  $$
  R_{max}=[\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3S_{simin}}]^{1/4}
  $$

  • 若雷达的检测门限设置为最小输出信噪比$(SNR){omin}$，则最小可检测信号功率为：
    $$
    S{min} = kT_0 BF(SNR)_{omin}(W)
    $$

  • 将上式代入雷达方程$R_{max}$，并用$L$表示雷达各部分的功耗（用L表示损耗而加在雷达方程的分母中，L是大于1的值。损耗L包括许多比较容易确定的值，诸如波导传输损耗、接收机失配损耗、天线波束形状损耗等，损耗L中还包括一些不易估计的值，例如操纵员损耗、设备工作不完善损耗等，这些因素要根据经验和实验测定来估计），可得到：
    $$
    R_{max}=[\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3kT_0 BFL(SNR)_{omin}}]^{1/4}
    $$

• 一般情况下，可近似认为带宽为时宽的倒数，即$B\approx \frac{1}{\tau}$

3.单基地雷达方程

• 理想无损耗、自由空间传播的单基地雷达方程，且假设信号从天线方向图最大增益处发射、接收
  $$
  P_r=\frac{P_tG_t}{4\pi R^2}\times\sigma\times\frac{A_r}{4\pi R^2}
  $$

• 收发不同天线：
  $$
  R_{max}=[\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3S_{simin}}]^{1/4}
  $$

• 收发天线共用：
  $$
  R_{max}=[\frac{P_tG_r^2\lambda^2\sigma}{(4\pi)^3S_{simin}}]^{1/4}
  $$

目标的散射截面积(RCS)

• 定义式

$$
\sigma=\frac{P_2}{S_1}
$$

• 其中，$P_2$为散射总功率，$S_1$为入射功率密度

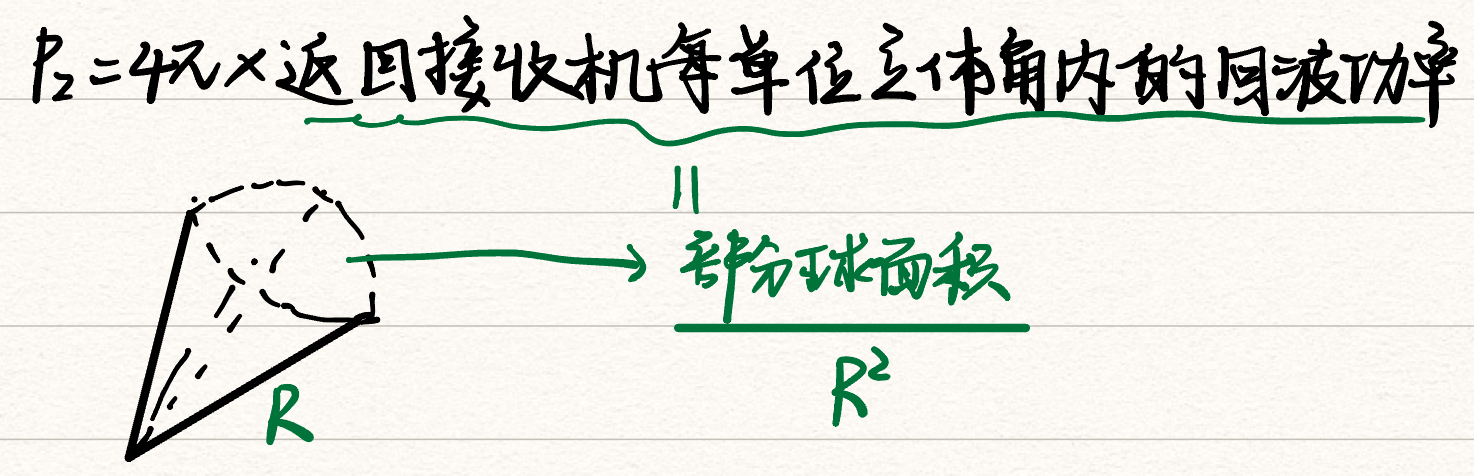
• $P_2=4\pi\times返回接收机每单位立体角内的回波功率$

  

• 测量：

  • 标准截面积$\sigma_0$满足：
    $$
    P_{ro}=k\frac{\sigma_0}{R_0^4}
    $$

  • 若未知目标处于R处，测$P_r$：
    $$
    P_r=k\frac{\sigma}{R_0^4}
    $$

  • 将上式两式相比，可以得到$\sigma$：
    $$
    \sigma=\frac{P_r}{P_{r0}}\cdot\frac{R^4}{R_0^4}\cdot\sigma_0
    $$

---

最小可检测信号

1.最小可检测信号与信噪比

• 如果只有信号而没有噪声，任何微弱信号在理论上都可以经过任意放大之后被检测到，因此，雷达检测能力实际上取决于信号噪声比

• $S_{imin}=kT_0BFM$，其中M又称为检测因子$D_0$​。定义为接收机匹配滤波器输出端（检波器输入端）测量的信号噪声功率比
  $$
  M=(\frac{S}{N})_{omin}
  $$

• 将$S_{imin}$带入雷达方程，得到：
  $$
  R_{max}=[\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3kT_0BFD_0}]^{1/4}
  $$

2.门限检测

• 由于噪声的存在，判断信号是否出现就成了一个统计问题，必须根据某种统计检测标准进行判断

• 奈曼-皮尔逊准则：要求在给定信噪比条件下，满足一定虚警概率$P_{fa}$时的发现概率$P_d$ 最大。

• 接收检测系统首先在中频部分对单个脉冲信号进行匹配滤波，接着进行检波，通常是在n个脉冲积累后再检测，将积累输出与某一门限电压进行比较，若输出包络超过门限，则认为有目标存在，否则认为没有目标，这就是检测门限。

• 门限检测是一种统计检测，由于信号叠加有噪声，因而总输出是一个随机量。在输出端根据输出振幅是否超过门限来判断有无目标存在，可能出现以下四种情况:

  • 无目标时：
    • $V\ge V_T$：判断为有目标，此时称为虚警，则有虚警概率$P_{fa}$
    • $V<V_T$：判断为无目标，此时称为正确不发现，则有正确不发现概率$P_{an}=1-P_a$
  • 有目标时：
    • $V\ge V_T$：判断为有目标，此时称为正确发现，则有发现概率$P_{d}$
    • $V<V_T$：判断为无目标，此时称为漏报，则有漏报概率$P_{la}=1-P_d$

3.检测性能与信噪比

3.1 虚警概率

• $P_{fa}=\int_{V_T}^\infty w(x|无目标)dx$，其中高斯噪声的包络服从瑞利分布$w(x|无目标)=\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}}$

• 则$P_{fa}=e^{-\frac{V_T^2}{2\sigma}}$，$\sigma$为噪声的均方根值，

• 虚警时间与虚警概率的关系

  

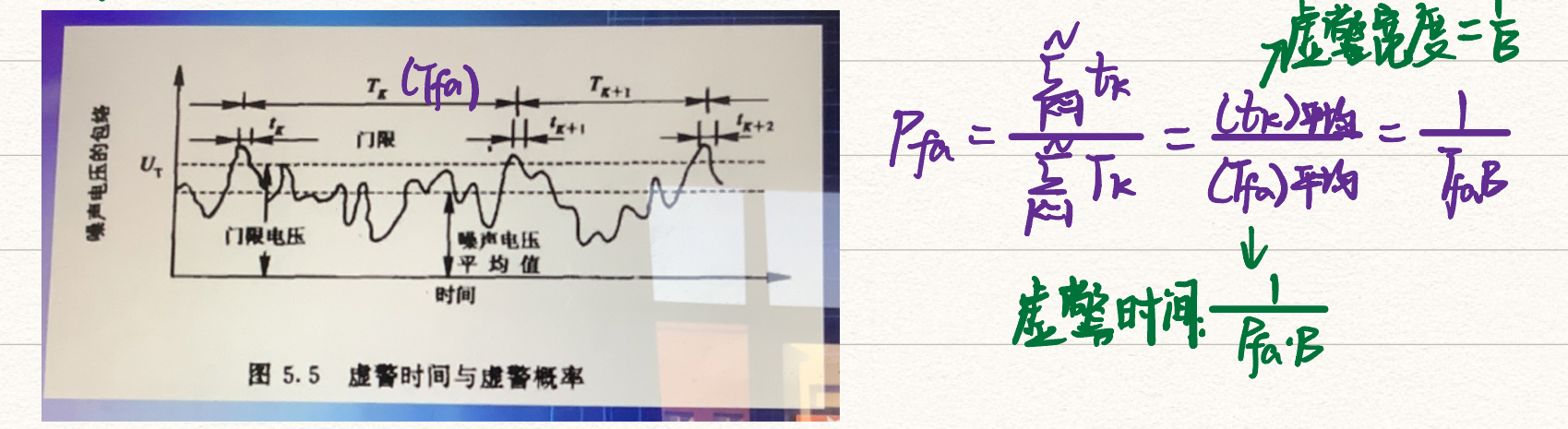
• 虚警数：$n_f=\frac{1}{P_{fa}}$，出现一次虚警所需要的次数

3.2 发现概率

• $P_{fa}=\int_{V_T}^\infty w(x|有目标)dx$

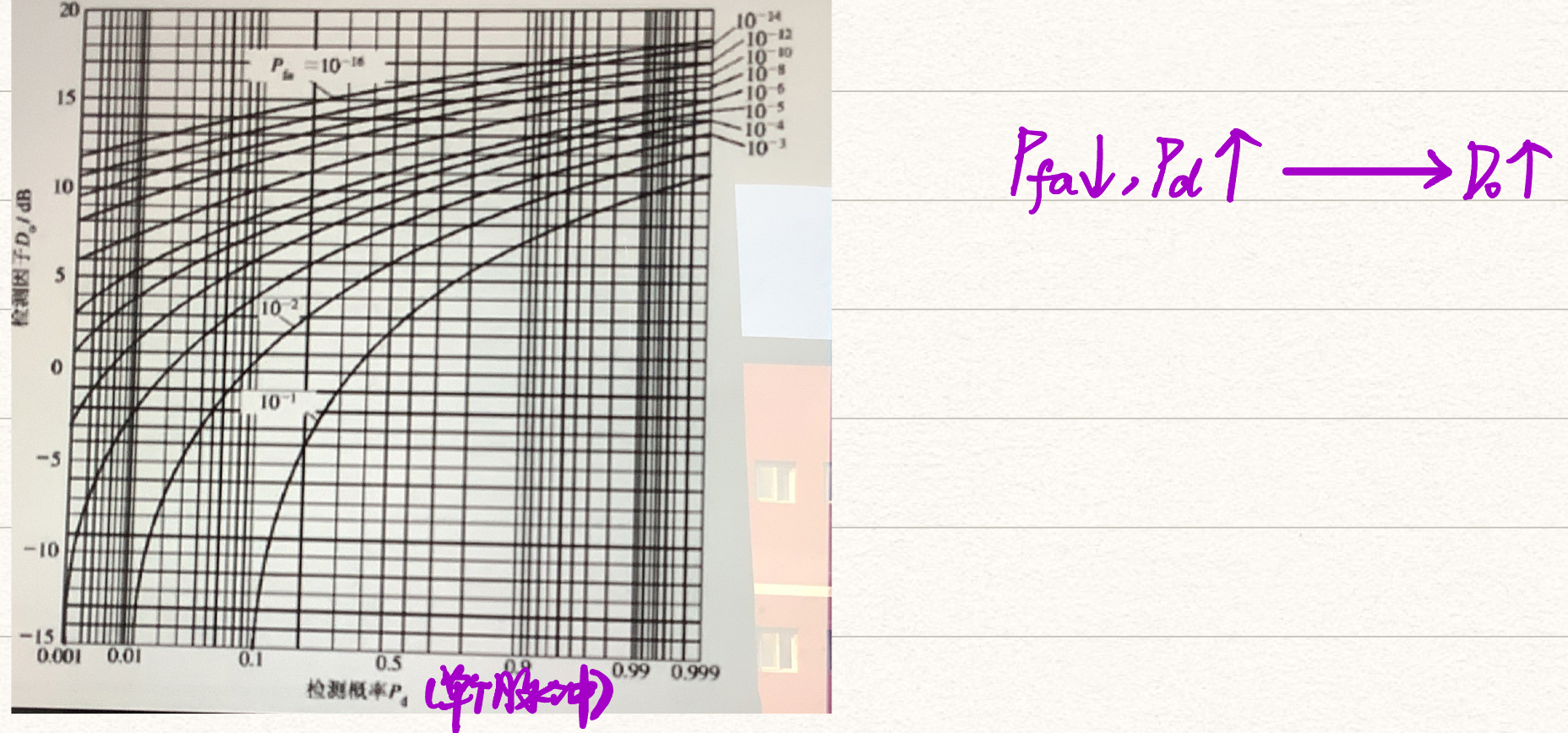
• 此时有目标，$w(x|有目标)$服从广义瑞利分布，通过查表查找

  

---

脉冲积累对作用距离的改善

1.相参积累

• 假设$ω$为天线扫描角速度。$\frac{θ_{0.5}}{ω}$ 为扫过3dB带宽所需时间，在此时间接收机都能接收到回波信号。

• 则能接收到的脉冲积累个数为：
  $$
  w=\frac{\theta_{0.5}}{w}f_r
  $$

• 单个脉冲回波信号：其功率为$A^2$，噪声功率为$\sigma^2$
  $$
  Acos(2\pi f_0+\phi_0)
  $$

• $M$个脉冲相参积累（$\phi$相同）后：其功率为$M^2A^2$，噪声功率为$M\sigma^2$
  $$
  MAcos(2\pi f_0t+\phi_0)
  $$

• 故相参后信号噪声比为：
  $$
  \frac{M^2A^2}{M\sigma^2}=M\frac{A^2}{\sigma^2}
  $$

• 则相参积累后，信噪比扩大了M倍

• 定义$D_0(M)$：M个脉冲积累之后，每一个脉冲所需的信噪比
  $$
  D_0(M)=\frac{D_0(1)}{M}
  $$

  

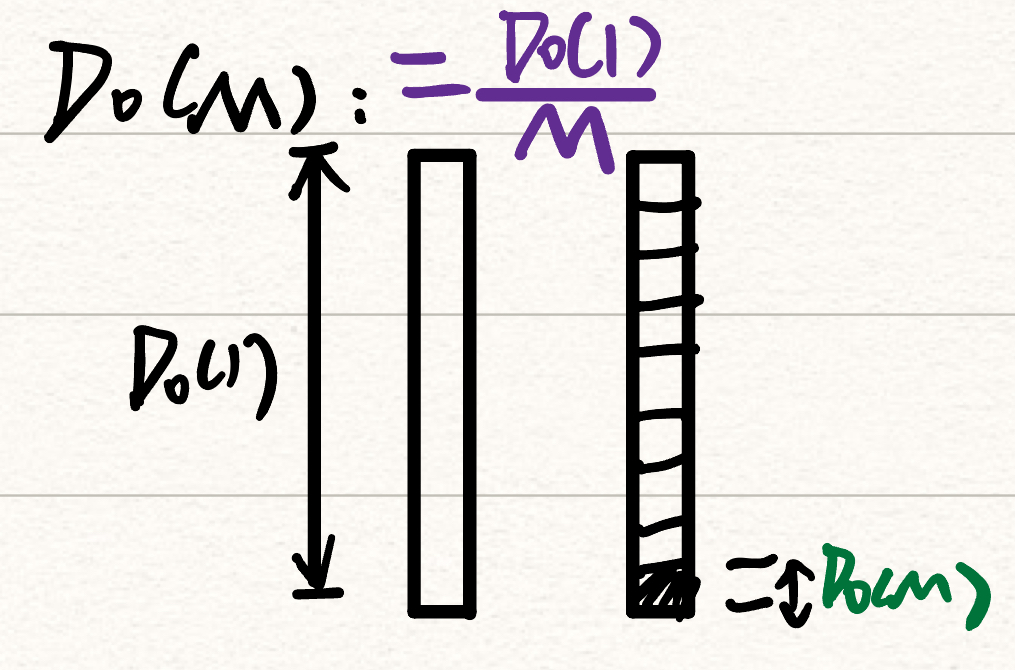
• 相参积累后，最大作用距离变为：
  $$
  R_{max}’=R_{max}\sqrt[4]M
  $$

2.非相参积累

• 每个回波脉冲的初始相位$\phi$是有变化的。所以，积累之后幅度不能增加 M 倍
• 通过查表得方式查找$D_0(M)$

3.脉冲积累数的确定

---

目标截面积及其起伏特性

1.点目标

1.1 距离分辨率

• 距离分辨率用于描述雷达分别探测出相邻目标的能力
• 如果两个目标的间距至少为$\frac{C\tau}{2}$，那么当脉冲后沿撞上第一个目标时，这个脉冲的前沿才开始从第二个目标返回将产生两个分开的返回脉冲。当两个目标的间距小于$\frac{C\tau}{2}$时，返回的脉冲将包括两个目标的回波（即未分辨的回波)。
• 则$距离分辨率=\frac{C\tau}{2}$

1.2 角度分辨率

• 角度分辨率是由天线的波束宽度决定的
• 即使两个散射体位于同一距离的不同方位，只要它们都在天线的主瓣内，它们都会被同时照射到，它们的回波也会同时被雷达接收
• 采用天线的3dB波束宽度作为主瓣宽度，这样位于波束3dB边缘的两个点散射体就定义了雷达的角度分辨率

1.3 雷达三维分辨单元

• 如果两个目标同时落在同一个距离单元，也在同一个角度单元，雷达就无法区分这两个目标，我们就把距离单元和角度单元构成的一个三维单元称为雷达三维分辨单元$\Delta V$

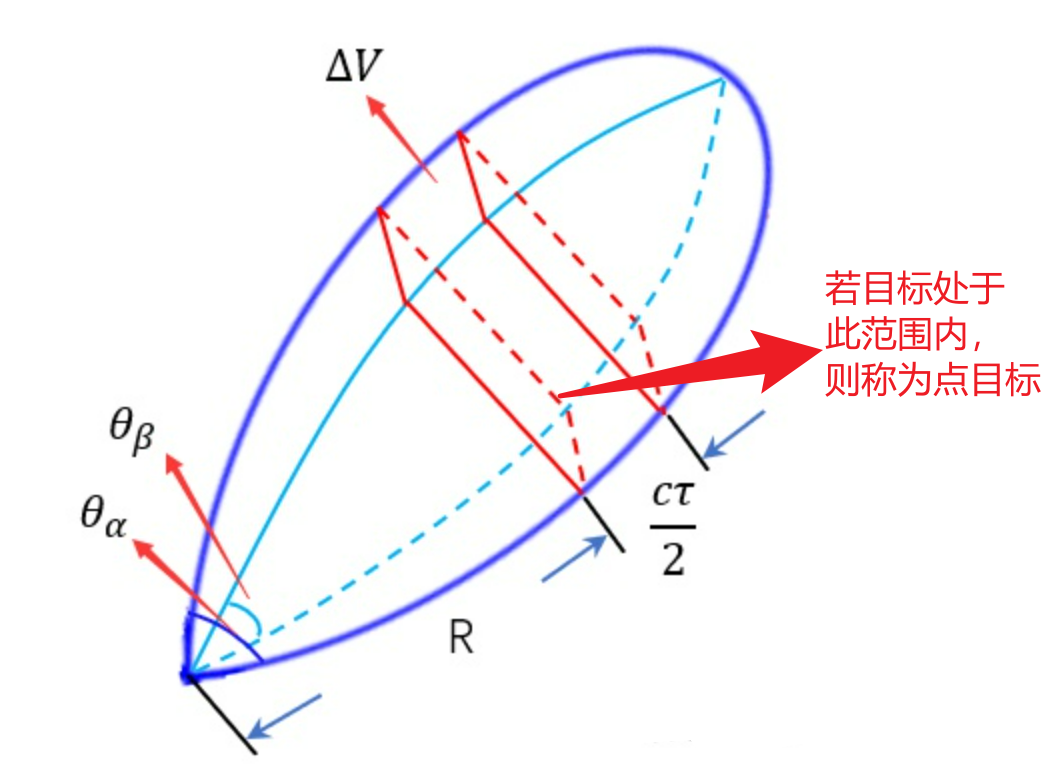
• 如果目标体积满足：$V<ΔV$，就称之为点目标。

1.4 点目标横截面积与波长的关系

• 最理想的点目标是一个各向同性的球体。设$r$为各向同性球体的半径。

• 当雷达照射球体时，分为三种情况：

  • 瑞利区：$λ>>2πr，σ∝λ−4$
  • 振荡区：$λ≈2πr，σ在πr^2附近振荡$
  • 光学区：$λ≤2πr，σ≈πr^2$
  

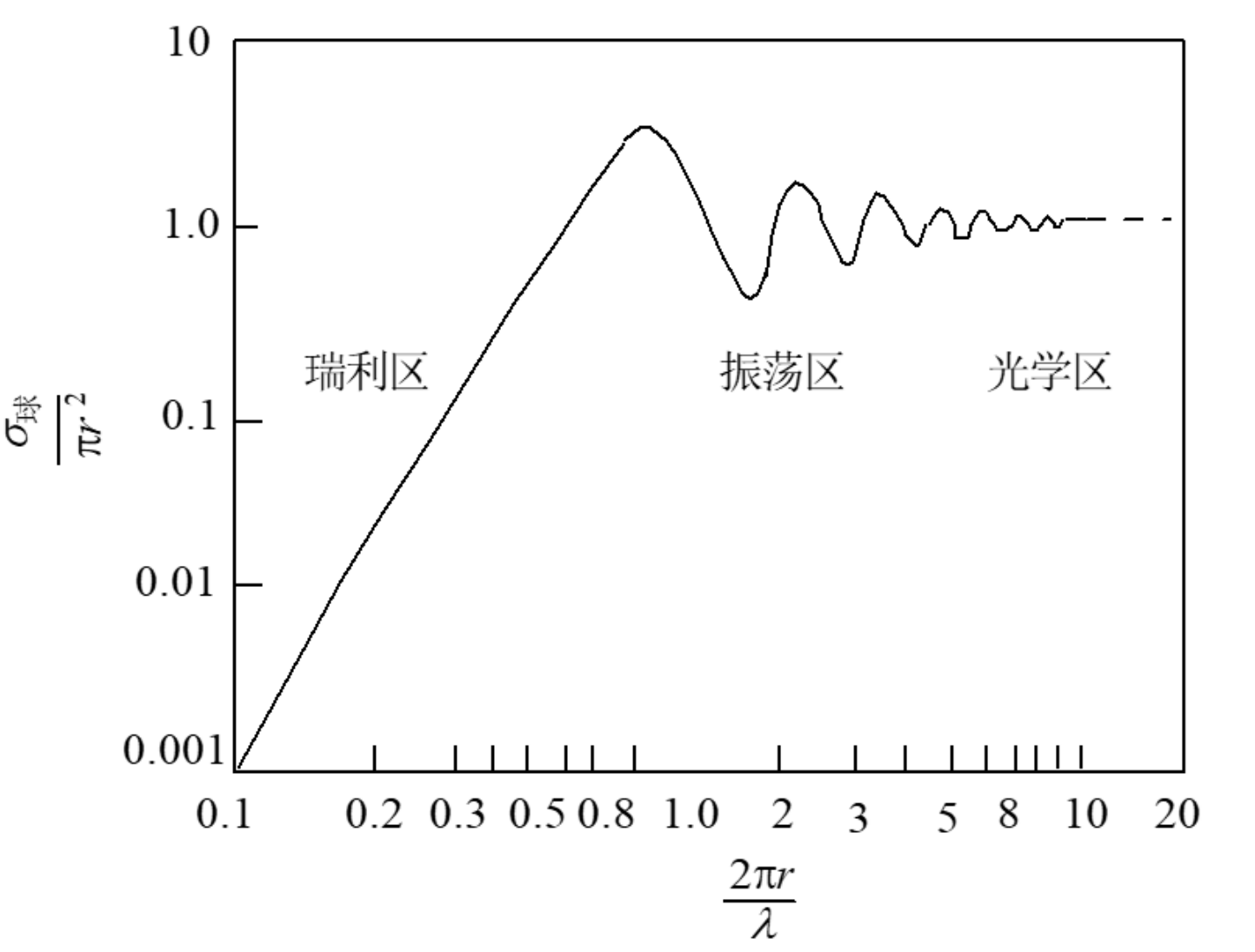
• 我们希望点目标处于光学区。实际上大多数目标都处在光学区

2.简单形状目标的雷达截面积

• 几何形状比较简单的目标，如球体、圆板、锥体等，它们的雷达截面积可以计算出来

3.复杂目标的雷达截面积

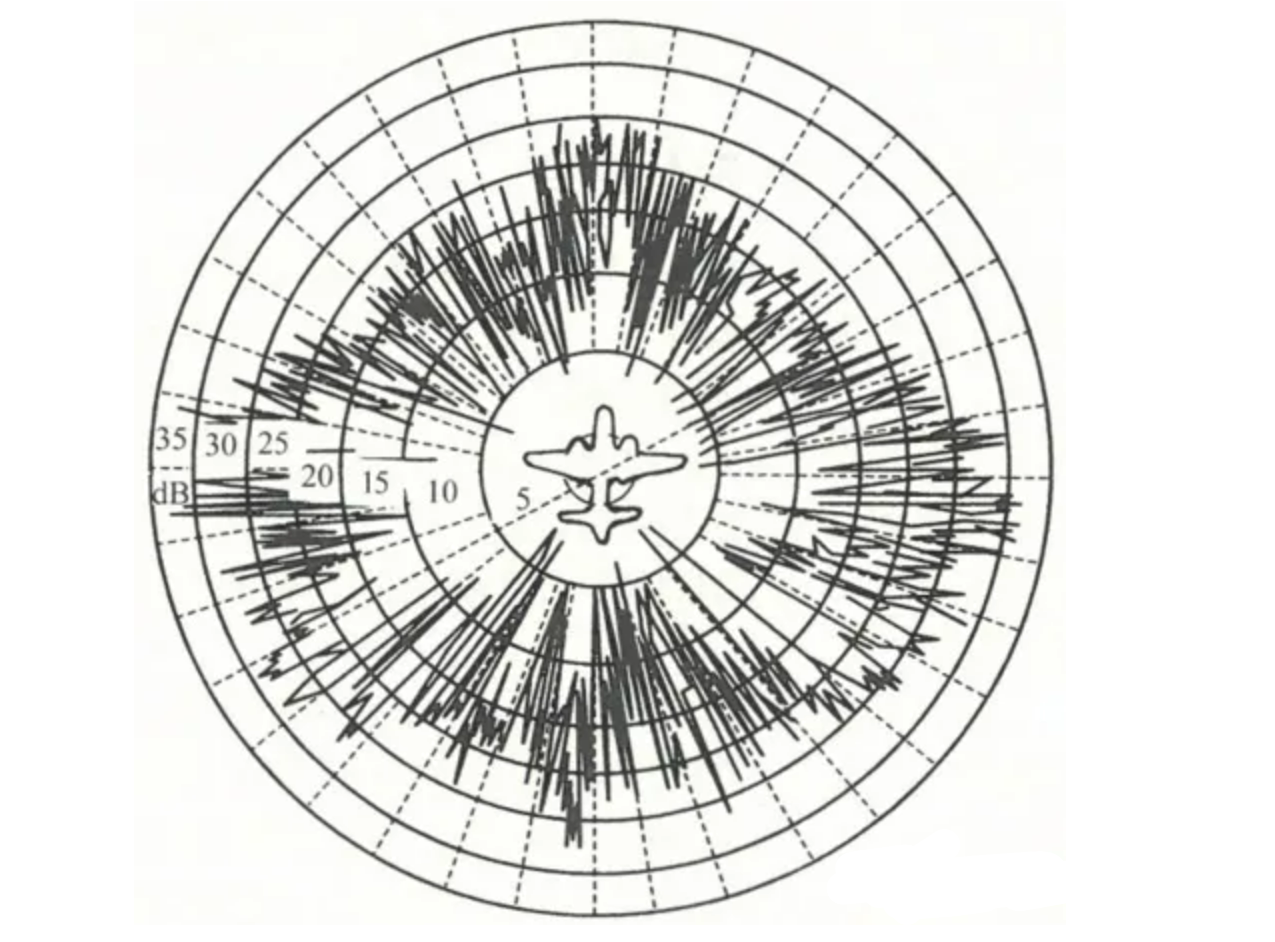
• 复杂目标是指雷达实际要探测的各种目标，如飞机、舰船、地物等
• 复杂目标的雷达截面积是不仅是视角的函数（也就是说雷达从不同方向照射目标，目标的雷达截面积会发生变化），同时也随频率、波长、极化等变化。通常雷达工作时，精确的目标姿态及视角是不知道的，因为目标运动时视角随时间变化。因此，最好是用统计的概念来描述雷达截面积。

4.目标反射特性与极化

• 极化：用来描述电场的方向。当电场的方向是垂直时，该电磁波被说成是垂直极化；当电场的方向是水平时，该电磁波被说成是水平极化。
• 当波被反射时，被反射波的极化不仅取决于入射波的极化，还取决于反射体的结构。事实上，雷达回波的极化可被用于辅助辨别目标的类型。

4.1 线极化（水平极化、垂直极化）

• 将照射电场分解为$E_H^T,E_V^T$，接收电场分解为$E_H^R,E_V^R$，有：

  
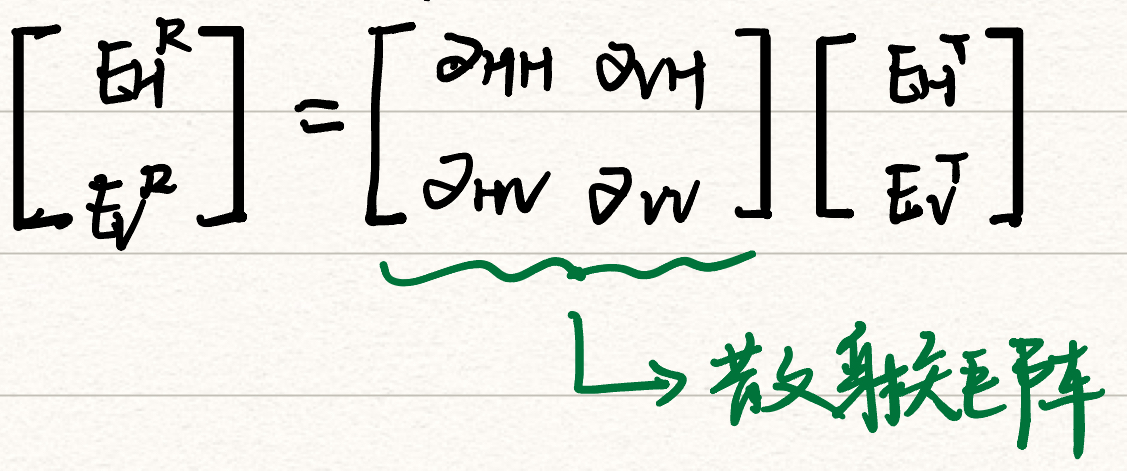
  • 散射矩阵：反映目标本身的散射特性。即目标对于照射它的电场变为接收电场，目标对于极化的影响。
  • $α_{HH}$表示水平极化入射场产生水平极化散射场的散射系数
  • $α_{HV}$表示水平极化入射场产生垂直极化散射场的散射系数
  • $α_{VH}$表示垂直极化入射场产生水平极化散射场的散射系数
  • $α_{VV}$表示垂直极化入射场产生垂直极化散射场的散射系数

• 特殊形体目标的散射矩阵

  • 各项同性的球体

    

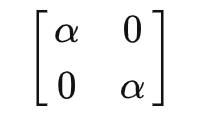
  • 相对于入射方向对称的物体

    

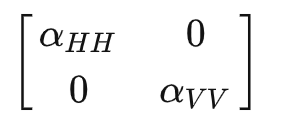
4.2 圆极化（左旋、右旋）

• $E_R^T，E_L^T$分别表示发射场中的右旋和左旋圆极化成分， $E_R^S，E_L^S$分别表示散射场中右旋和左旋圆极化成分。

• 相对于入射方向对称的物体

  

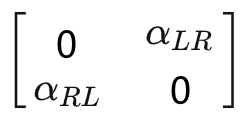
5.目标起伏对检测性能的影响

• 目标雷达截面积的大小对雷达检测性能有直接的关系，在工程计算中常把截面积视为常量。实际上，处于运动状态的目标，视角一直在变化，截面积随之产生起伏。

• 目标起伏模型

  

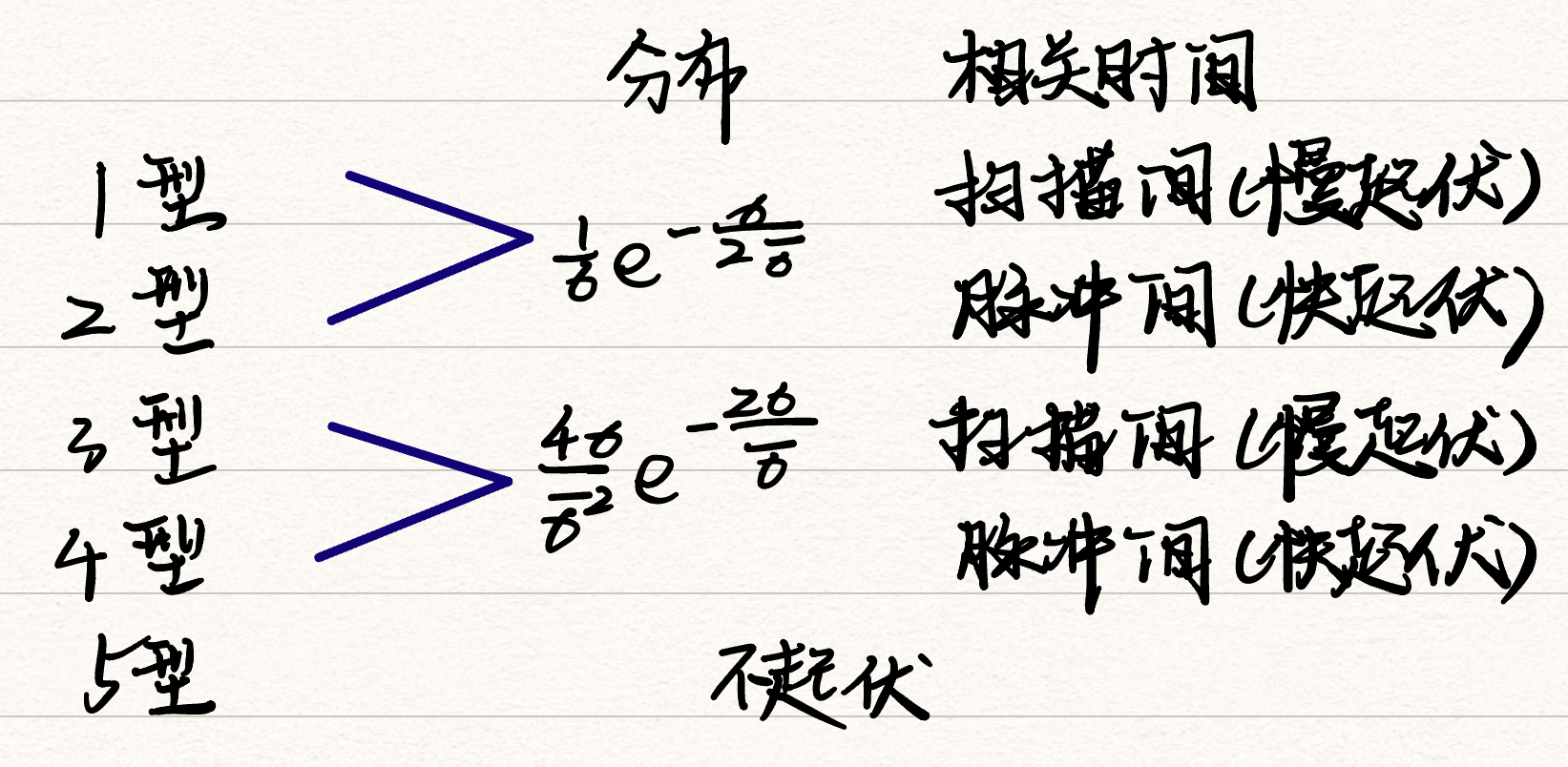
  • 扫描间：指的是同一个周期内的M个回波间是有相关性的，不同周期扫描间的回波是没有相关性的。说明目标本身起伏特性的变化比较慢

  • 脉冲间：指的是同一个扫描周期内的M个回波间不具有相关性，说明目标本身起伏特性的变化很快

  • 由于目标起伏引起检测困难，$D_0$增加

    

---

雷达方程的几种形式

1.二次雷达方程

• 雷达发射信号，应答器接收
  $$
  P_r’=\frac{P_tG_t}{4\pi R_1^2}A_r’=\frac{P_tG_t\lambda^2G_r’}{(4\pi)^2R_1^2}
  $$
  则：
  $$
  R_{1max}=[\frac{P_tG_tG_r’\lambda^2}{(4\pi)^2S_{imin}’}]^{1/2}
  $$

• 应答器发射信号，雷达接收
  $$
  R_{2max}=[\frac{P_t’G_t’G_r\lambda^2}{(4\pi)^2S_{imin}}]^{1/2}
  $$

• 则$R_{max}$：
  $$
  R_{max}=\lbrace R_{1max},R_{2max}\rbrace
  $$

2.双基地雷达方程

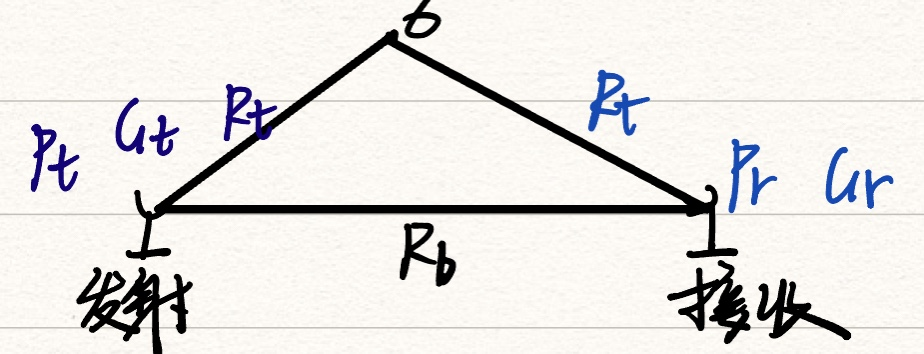
• 根据基本雷达方程有：
  $$
  P_r=\frac{P_tG_t}{4\pi R_t^2}\cdot\sigma\cdot\frac{A_r}{4\pi R_r^2}=\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3R_t^2R_r^2}
  $$

$$
则:R_{max}=R_tR_r=[\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3S_{imin}}]^{1/2}
$$

• 限制条件：
  $$
  R_t+Rr\ge R_b
  $$

  $$
  |R_t-R_r|\le R_b
  $$

3.用信号能量表示的雷达方程

$$
R_{max}=[\frac{EG_t^2\lambda^2\sigma}{(4\pi)^3kT_0FD_0C_B}]^{1/4}
$$

$$
其中，C_B是失配损失，E=P_t\tau
$$

4.干扰情况下的雷达方程

4.1 有源干扰（干扰机）

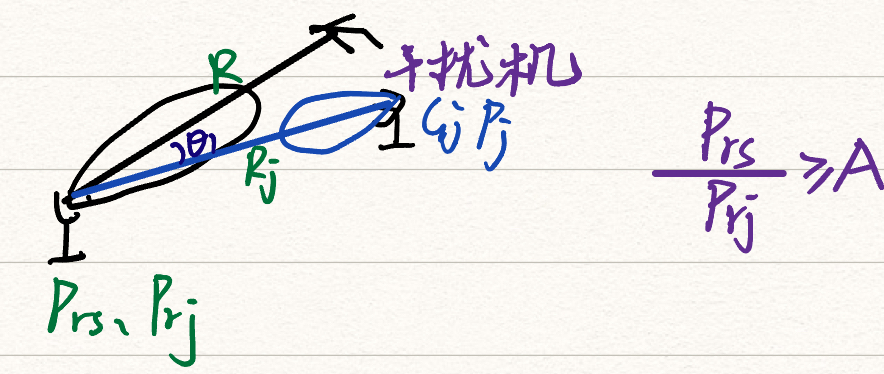
• 雷达要想检测到目标，必须满足：信号功率/（噪声功率+干扰功率）> 某个门限，即$\frac{P_{rs}}{P_{rj}}\ge A$（忽略噪声功率）

• 雷达接收到的目标回波信号功率$P_{rs}$：
  $$
  P_{rs}=\frac{P_tG_tG_r\lambda^2\sigma}{(4\pi)^3R^4L}
  $$

• 雷达接收到的干扰信号功率$P_{rj}$：

  $$ P_{rj}=\frac{P_jG_jA_r'}{4\pi R_j^2}\times\frac{\Delta f_r}{\Delta f_j} $$

  $$
  其中:G_r’=\frac{4\pi A_r’}{\lambda^2}=G_rF(\theta)
  $$

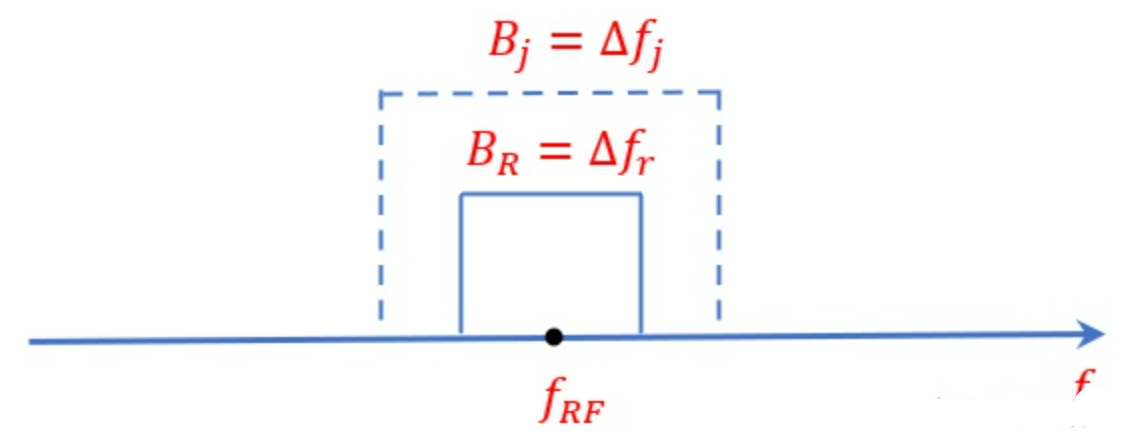
• 当$\frac{P_{rs}}{P_{rj}}=A$时，作用距离最大，有：
  $$
  R_{max}=[\frac{P_tG_tG_r\sigma R_j^2\Delta f_j}{4\pi P_jG_jG_r’\Delta f_rAL}]^{1/4}
  $$

• 自卫干扰：将干扰机放到目标上

  • $R_j=R,G_r’=G_r$
  • $R_{max}=[\frac{P_tG_t\sigma\Delta f_j}{4\pi P_jG_j\Delta f_rAL}]^{1/4}$

4.2 无源干扰（箔条干扰）

---

雷达基本方程的Python实现

import numpy as np
import matplotlib.pyplot as plt 

def radar_basic_eq(pt, freq, G, sigma, b, NF, L, snr):
    c = 3.0e8 #光速
    t0 = 290
    lambda1 = c/freq

    num1 = 10 * np.log10(pt * 1.0e3 * lambda1 ** 2) + 2 * G +sigma
    num2 = 10 * np.log10((4.0 * np.pi) ** 3 * (1.38e-23) * t0 * b) + NF + L
    range_db = num1 * np.ones((1, len(snr))) - num2 - snr #shape = (3, 1)*(1, 100) - (100, )

    return range_db

pt = 1500 #峰值功率
freq = 5.6e9 #频率
G = 45 #天线增益
sigma = np.array([-10, 0, 10]) #目标截面积
sigma = sigma.reshape(len(sigma), 1)
b = 5.0e+6 #宽带
NF = 3 #噪声系数
L = 4 #雷达损耗
snr = np.linspace(10, 60, 100) #信噪比

range_db = radar_basic_eq(pt, freq, G, sigma, b, NF, L, snr)
range_km = 10 ** (range_db / 40)

fig = plt.figure()
for i in range(sigma.size):
    plt.scatter(snr, range_km[i] / 1000, label=f"sigma = {sigma[i][0]}") #range用km表示
plt.xlabel("SNR in dB",fontsize=12)
plt.ylabel("Range in km",fontsize=12)
# plt.xlim(10, 60)
# plt.ylim(20, 100)
plt.title("Radar Equation")
plt.legend()
plt.show()

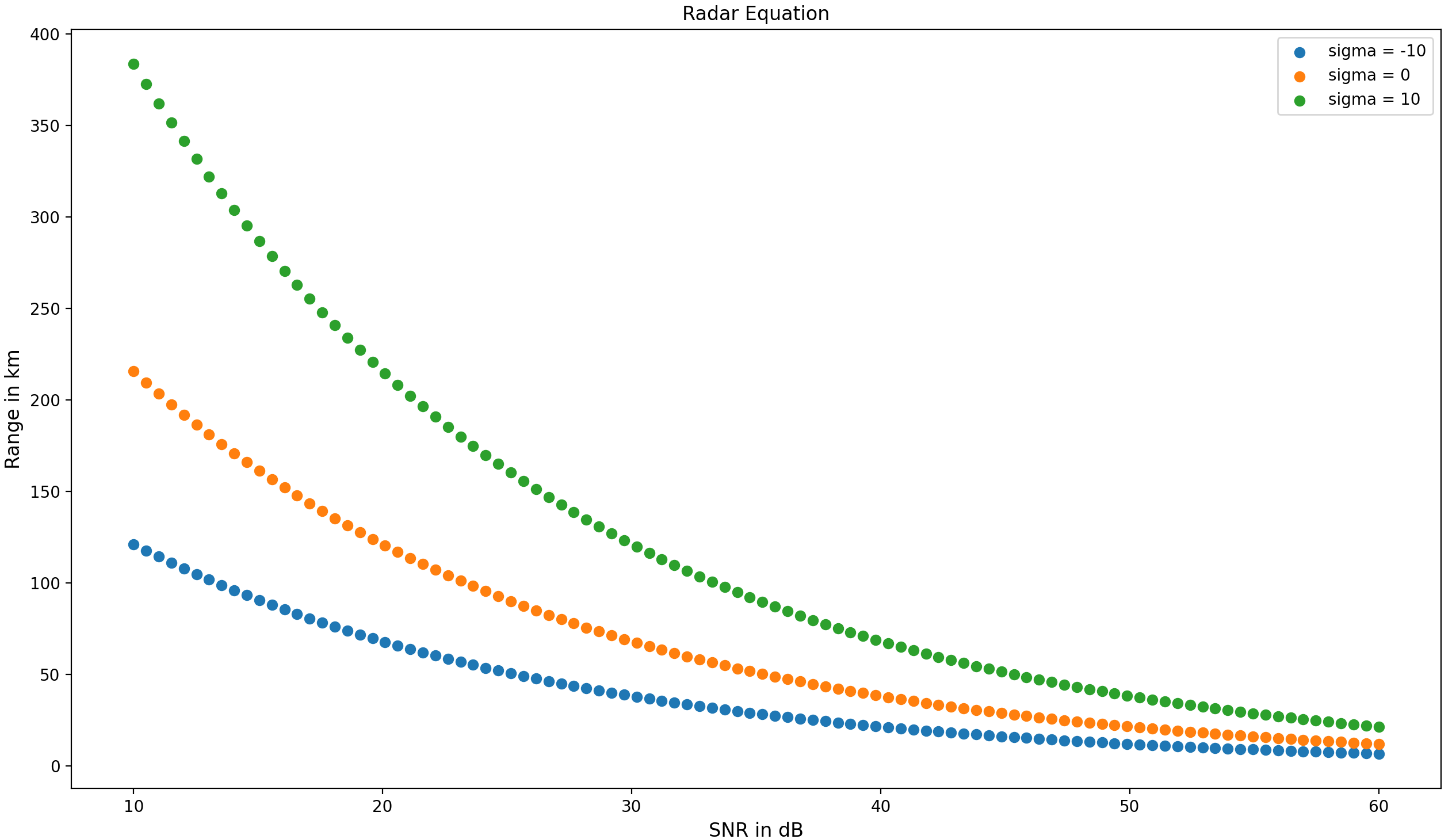
结果如下（最小输出信噪比与雷达作用距离之间的关系）：

---

Reference

• 五，雷达作用距离 - 知乎 (zhihu.com)