本节主要介绍了雷达原理中的基本概念,包括雷达的基本组成,目标参数的测量等。
雷达的基本组成
1.天线
- 发射信号并接收回波
2.发射机
- 产生雷达的发射信号
- 包括连续波信号与脉冲信号
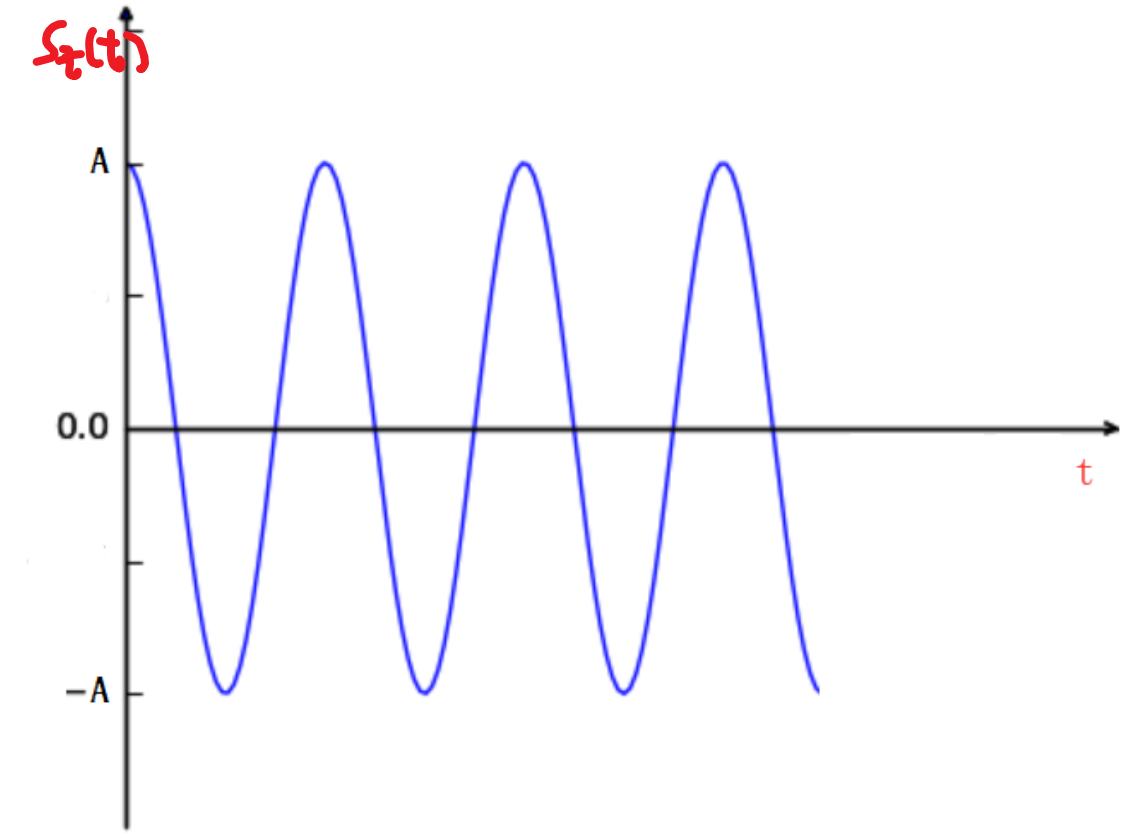
2.1 连续波信号
$S_t(t)=A_0cos(2\pi f_0t+\phi)$
- $S_t(t)$下标 t 表示 transmit
- $f_0$表示信号频率,即单位周期内波的个数,有$f_0=\frac{1}{T}$
- $f_0$与波长$\lambda$的关系:$\lambda f_0=C(光速)$
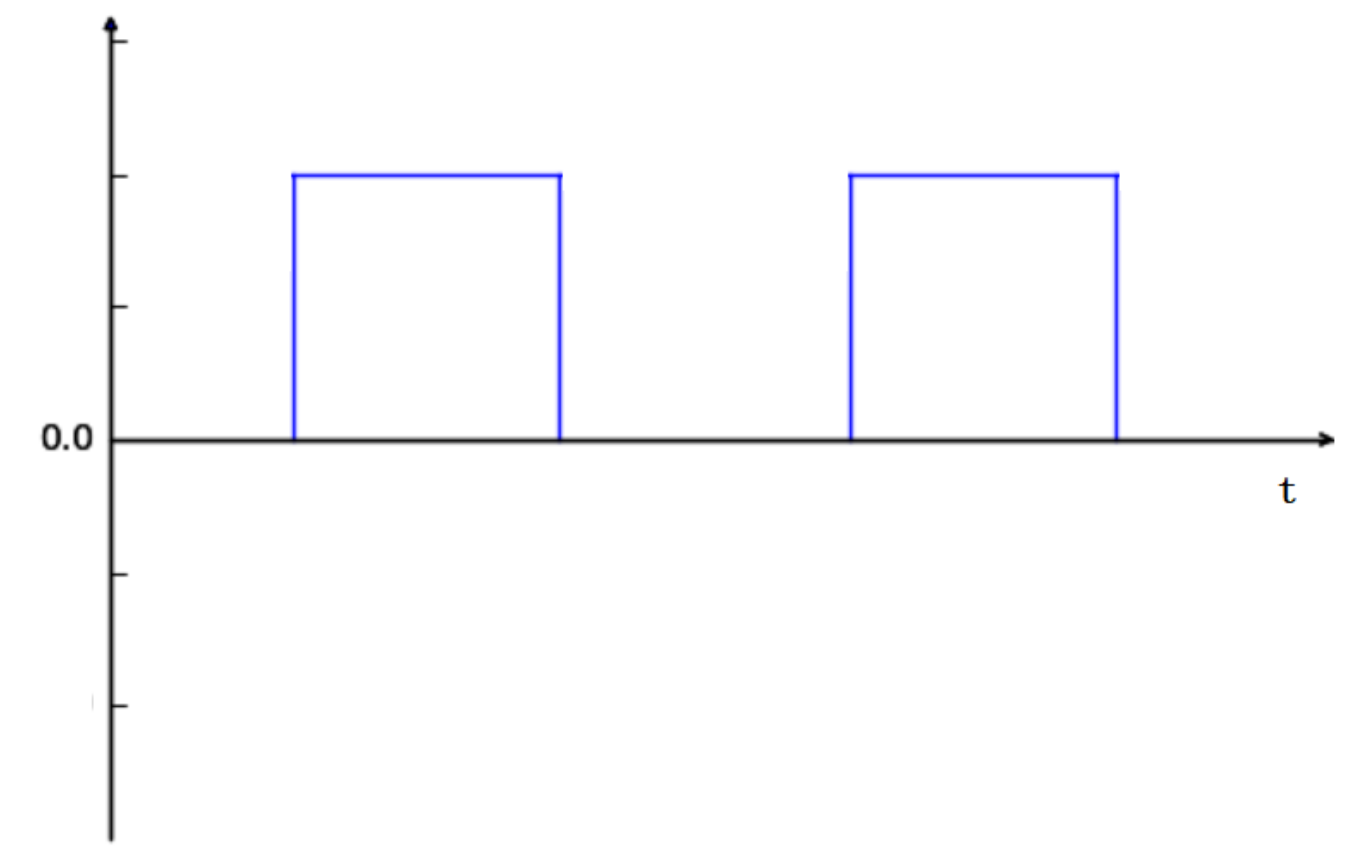
2.2 脉冲信号
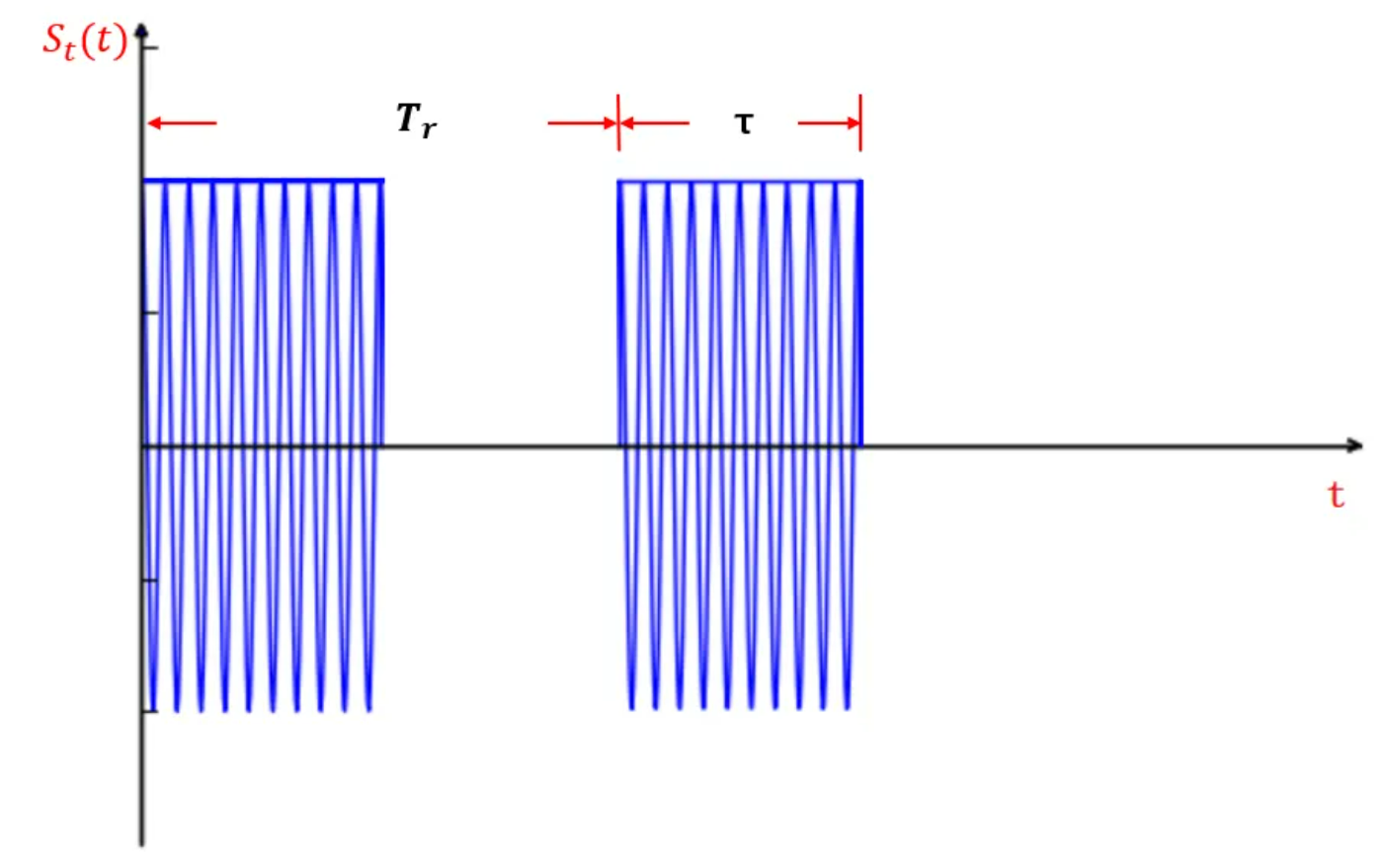
- $\tau$是脉冲宽度
- $T_r$是脉冲重复周期,则脉冲重复频率$f_r=\frac{1}{T_r}$
3.接收机
- 接收回波信号,并进行处理。一般会经历射频 -> 中频 -> 视频的处理过程
- 一般来说,如果要测距就需要做视频处理,根据发射信号和回波信号脉冲前沿的时间差,就可以计算得到目标距雷达的距离
- 如果要测速,就需要在中频进行处理。因为测速需要利用多普勒效应,需要获取发射频率和接收频率的频率差。视频信号已经丢失了载波信息,就无法获取频率信息了
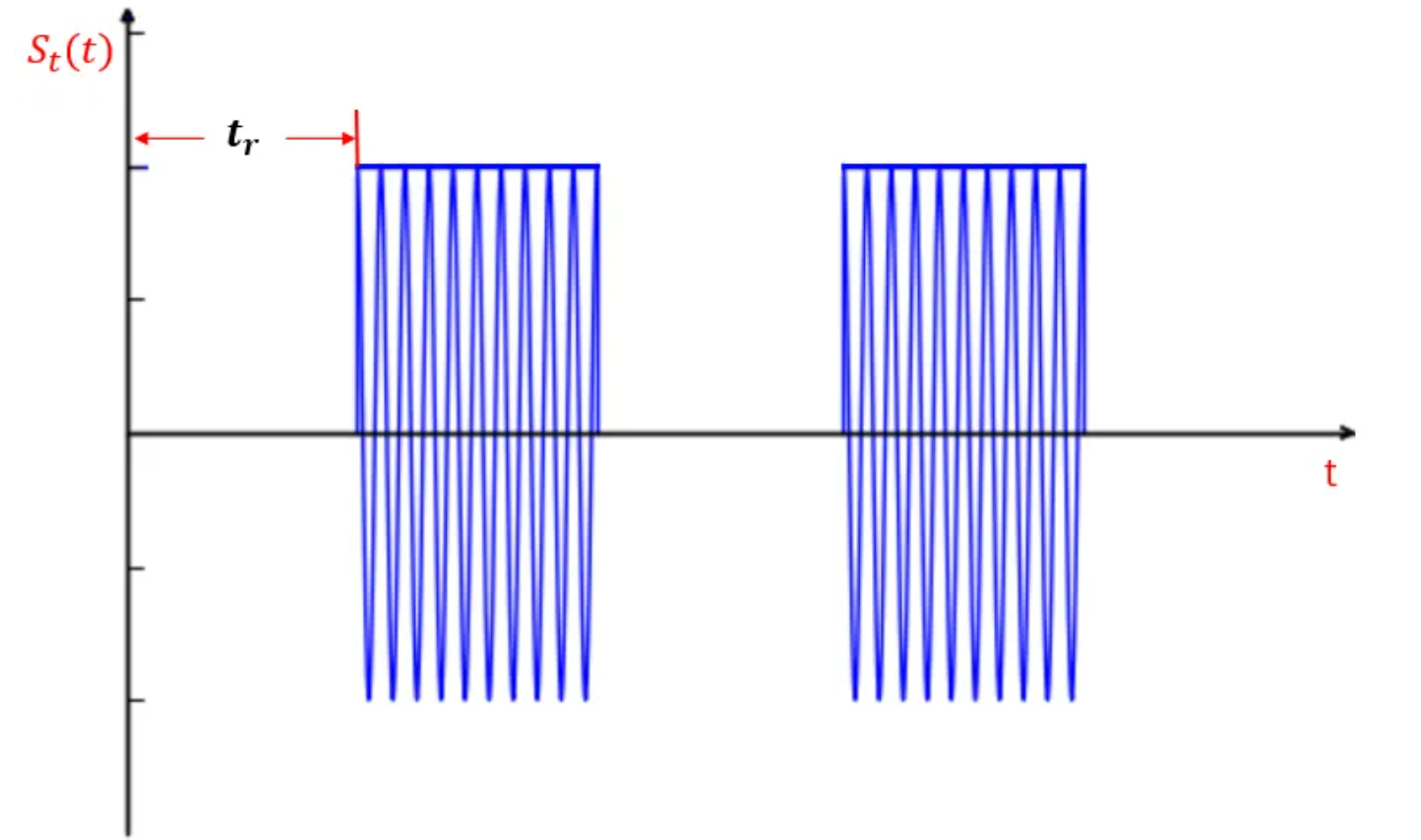
3.1 射频信号
- $t_r$为时延差
3.2 中频信号
- 接收机收到的是射频信号,频率本来就比较高,如果直接在射频上进行采样,根据奈奎斯特采样定理,采样频率需要大于信号频率的两倍,才能将采样后的信号无失真的还原回去。直接在射频上进行采样,成本就会很高,所以就需要对射频信号进行混频处理,变到中频,这样对采样率的要求就降低了
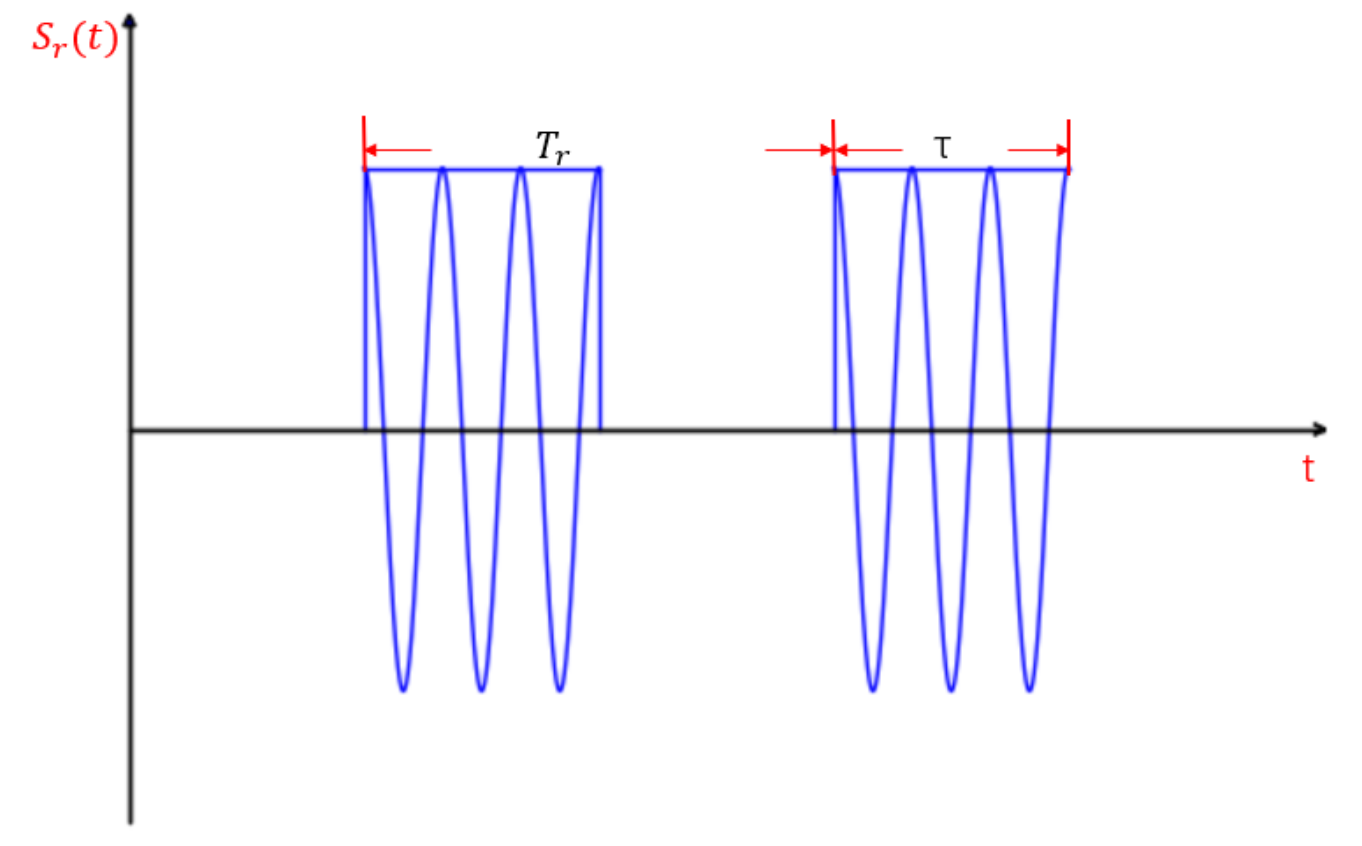
- 从图中可知,中频信号,频率虽然变低了,但是包络还是原来的包络
3.3 视频信号
- 中频信号经过包络检波就能得到视频信号
4.信号处理机
- 提取目标的各种信息
5.终端显示设备
- 将雷达探测到的目标信息,以可视化的方式显示到屏幕上
6.伺服系统与同步设备
- 伺服系统:控制天线转动,使天线指向不同角度,以探测不同方位的目标
- 同步设备:雷达的频率和时间标准。产生各种频率振荡,提供统一的时钟
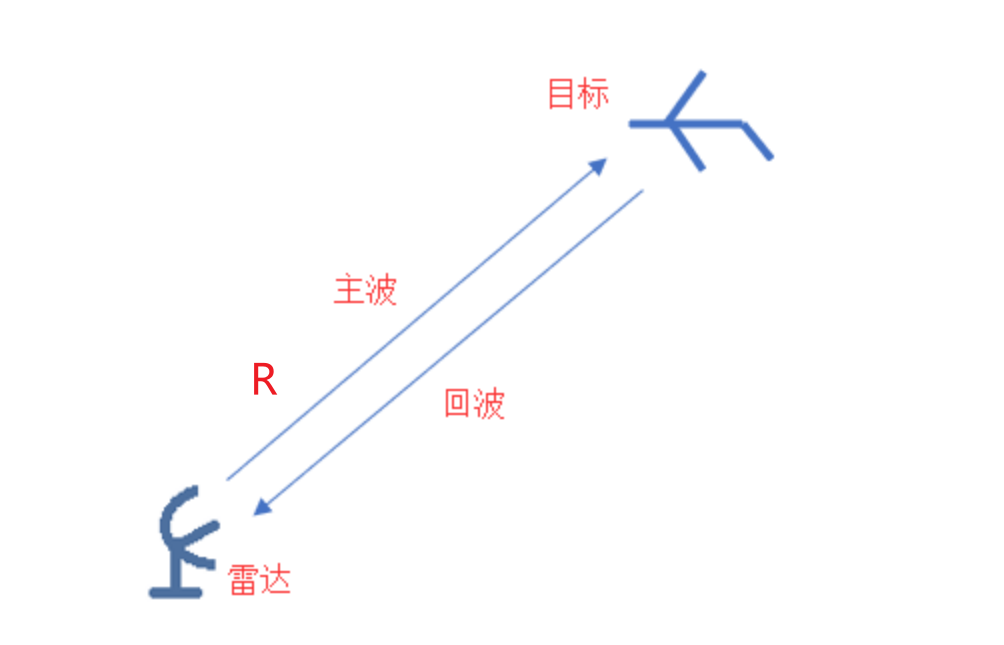
简单的目标距离测量
- $2R=Ct_r\Rightarrow R=\frac{Ct_r}{2}$
多普勒效率与速度测量
- 测速原理:利用多普勒效应
- 实际测量的是径向速度,目标和雷达之间必须有径向速度分量
1.多普勒效应
- 当目标与雷达之间存在相对速度时,接收到的回波信号的载频相对于发射信号的载频会产生一个频移$f_d$
- $f_d=f_r-f_t=\frac{2V_r}{\lambda}$
- $f_r$:回波信号的频率
- $f_t$:雷达发射信号的频率
- $V_r$:目标相当于雷达的径向速度
- $f_t$:信号波长
2.频率与相位的关系
- 瞬时相位$\xrightarrow{相对于时间求导}$瞬时角频率$\xrightarrow{\div2\pi}$瞬时频率
- 对于线性调频信号有:
- $S_t(t)=Acos(2\pi f_0t+\pi\mu t^2+\phi)$
- 瞬时频率$f(t)=\frac{\partial(2\pi f_0t+\pi\mu t^2+\phi)}{2\pi\partial t}=f_0+\mu t$
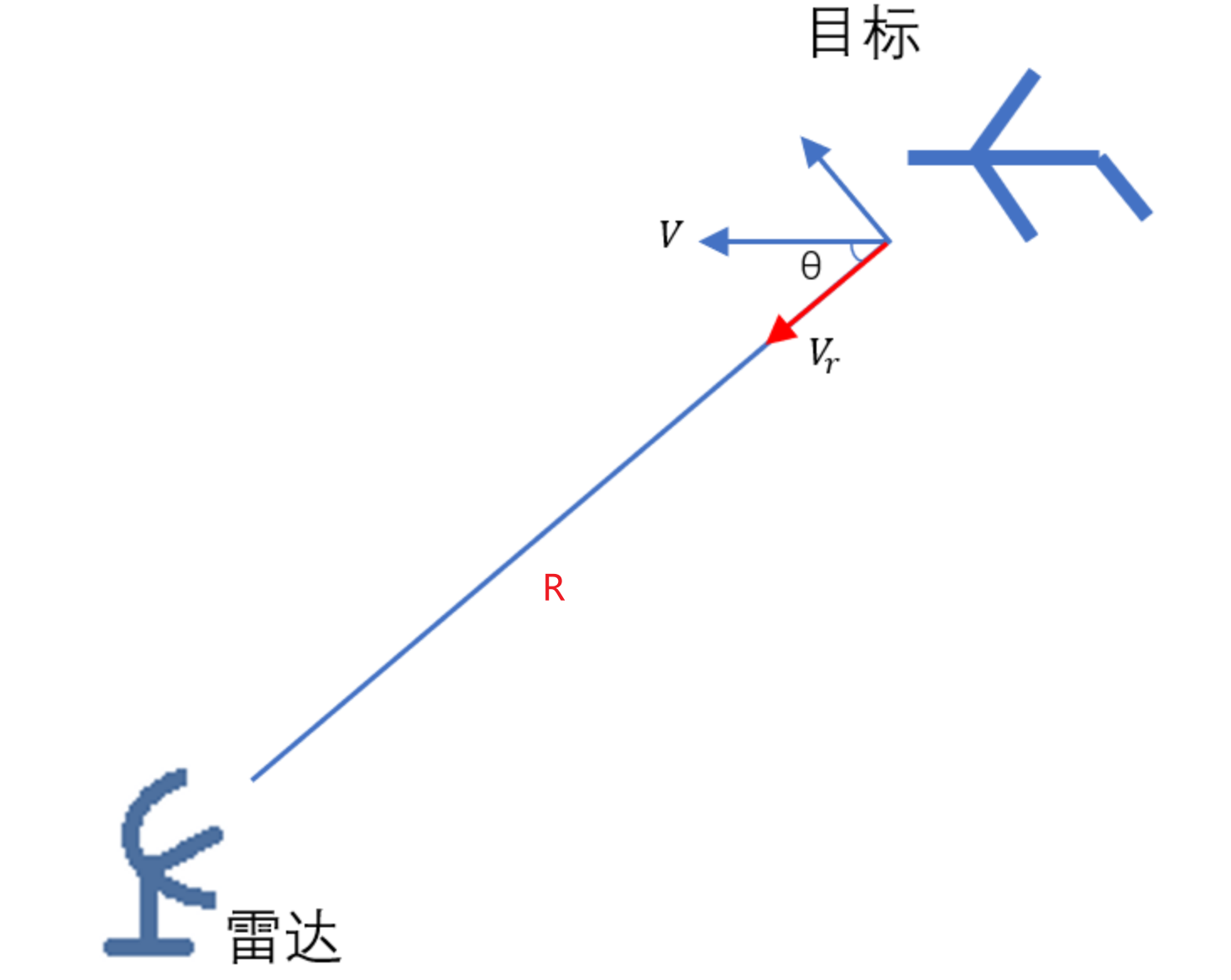
3.测速公式推导
径向速度:$V_r=Vcos\theta$
则当雷达发射信号到达目标时的距离为:$R=R_0-V_rt$
则回波信号为:$S_r(t)=kS_t(t-t_r)=kAcos(2\pi f_0(t-\frac{2(R_0-V_rt)}{C})+\phi)$
对$S_r(t)$求导并除以$2\pi$可以得到:$f_r=f_t+\frac{2V_r}{\lambda}$
即:$f_d=f_r-f_t=\frac{2V_r}{\lambda}$
当$f_d$为负数时,目标远离;当$f_d$为正数时,目标靠近
4.多普勒频率的详细解释与推导
当目标向着雷达运动时。多普勒频率为正;当目标远离雷达时,多普勒频率为负
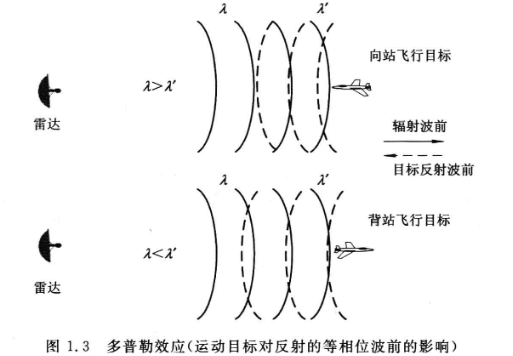
照射到目标上的波形具有间隔为$\lambda$(波长)的等相位波前:
- 靠近雷达的目标导致反射回波的等相位波前相互靠近(较短波长),$\lambda > \lambda’$($\lambda’$为反射波波长)
- 远离雷达运动的目标导致反射回波的等相位波前相互扩展(较长波长)$\lambda < \lambda’$
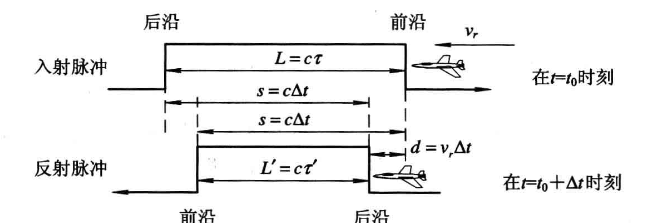
运动目标速度对发射脉冲的影响:
假设雷达的发射脉冲宽度为$\tau$,对应的波程为$L = c\tau$(c为光速),目标的径向速度为$v_r$
假设脉冲前沿到达目标与后沿到达目标的时间间隔为$\Delta t$,在$\Delta t$时间内目标移动脉冲内的距离为$d = v_r \Delta t$
由于脉冲以光速传播,后沿已经移动的距离是$c\tau - d$,那么:
由上式可得到反射脉冲宽度$\tau’$和入射脉冲宽度$\tau$之间的关系为:
式中,$\frac{c-v_r}{c+v_r}$通常称为时间扩展因子
若$v_r = 0$,则$\tau’ = \tau$
同理可计算,当目标以速度$v_r$远离雷达时,反射和入射脉冲宽度之间的关系为:
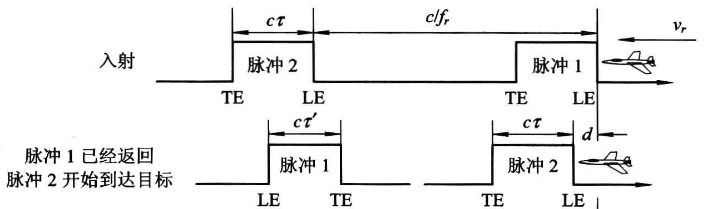
多普勒频率的推导:
假设两个入射脉冲的重复频率(PRF)为$f_r$,脉冲1的前沿到达目标以后,脉冲2的前沿要花$\Delta t$时间到达目标,电波传播的距离为$(\frac{c}{f_r}-d)$,且脉冲2前沿在$\Delta t$时间的迟延距离$d = v_r\Delta t$,则
经化简得:
反射脉冲间隔$T_r’$所对应的波程为$s-d$(下图是关于为什么反射脉冲间隔为s-d的个人见解),其中$s = c\Delta t$,则回波脉冲的重复频率$f_r’ = \frac{1}{T_r’}$,且:
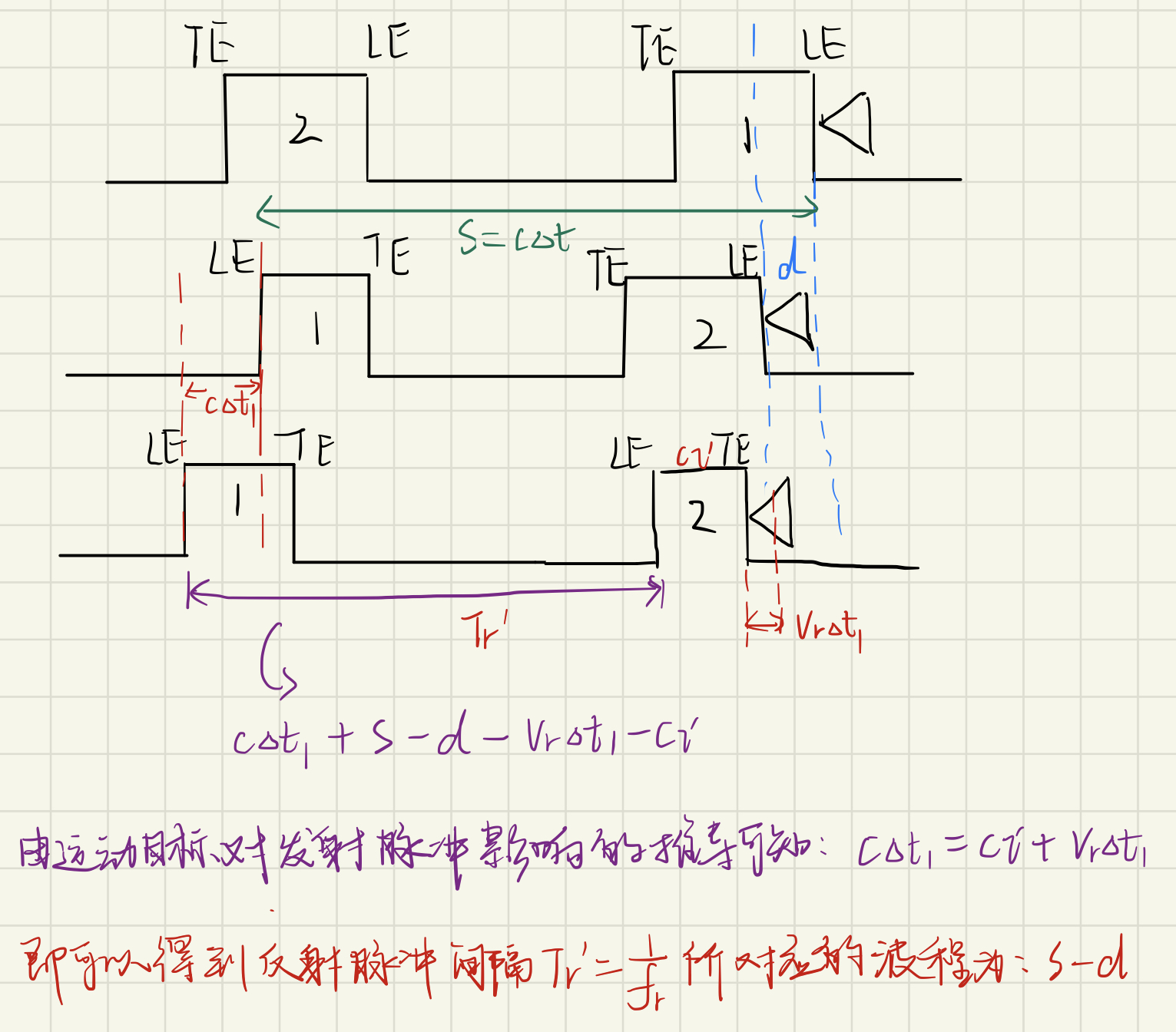
由此得到回波脉冲的PRF与入射脉冲的PRF之间的关系为:
由于周期的数量不变,反射信号的频率也以相同的因子上升,回波信号的载频$f_0’$与入射信号的载频$f_0$之间的关系为:
多普勒频率定义为回波信号的载频$f_0’$与入射信号的载频$f_0$之差,即:
由于$v_r<<c$,则波长$\lambda = c/f_0$,则:
影响多普勒频率的因素:
多普勒频率和雷达视线与目标运动方向之间的夹角有关
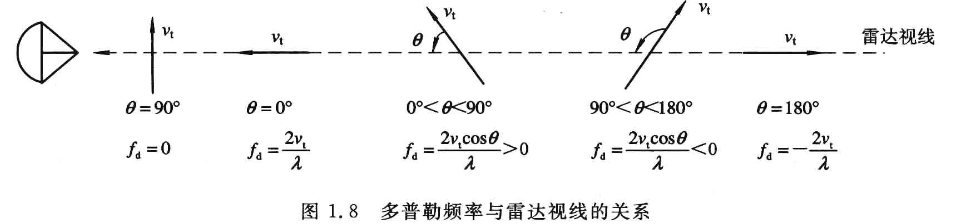
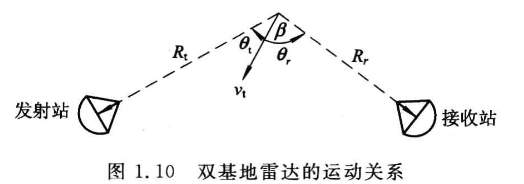
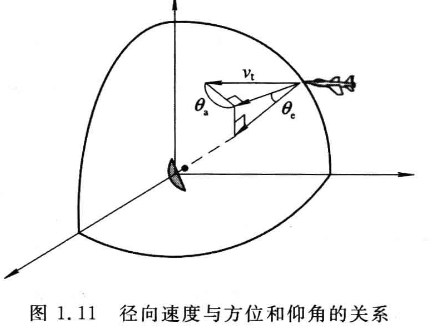
对于双基地雷达,若目标的运动方向相对于雷达视线的方位和仰角分别为$\theta_a$和$\theta_e$,则目标回波的多普勒频率为:
- 式中,$cos\theta = cos\theta_ecos\theta_a$,目标速度$v_t$投影到雷达实现的径向速度为$v_r = v_t cos\theta=v_tcos\theta_ecos\theta_a$
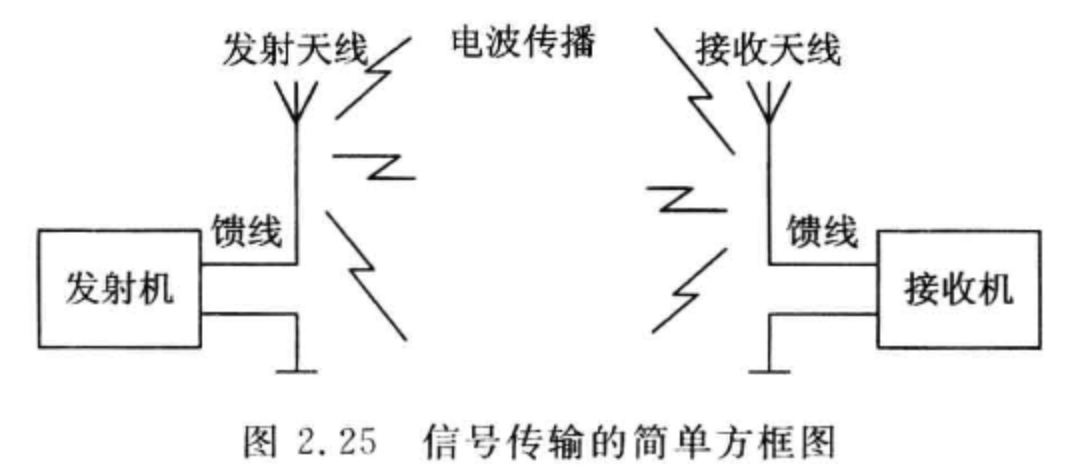
天线
- 定义:发射或接收系统中,经设计用于辐射和接收电磁波的部分
1.天线的基本功能
- 用于发射时,将高频电流(或导波)能量转化为无线电波并按照预定的分布传送到空间
- 用于接收时,将空间传来的无线电波能量转化为高频电流(或导波)能量
因此,天线可认为是导波和辐射波的变换转置,是一个能量转换器件
2.天线的主要性能指标
2.1 天线效率
发射机输出的功率为$P_G$,进入到天线的功率为$P_{in} = (1-|\eta|^2)P_G$ ,天线辐射的功率为$P_{\sum}$,
- $\eta$是反射系数
- 这是由于天线和传输线之间的失配而产生的,完全匹配时,$P_{in} = P_{P_G}$
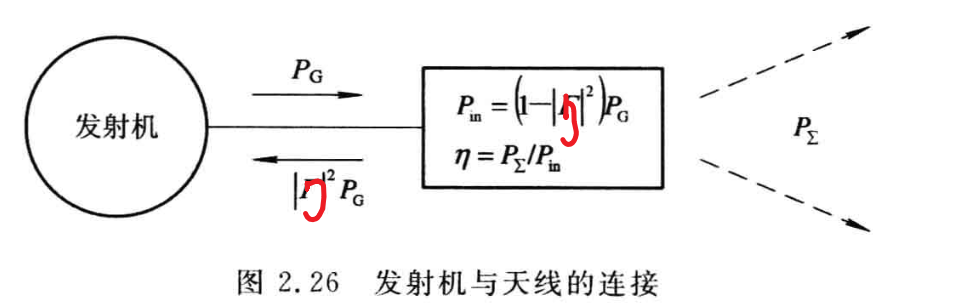
天线的效率定义为:
$P_{loss}$表示损耗功率,它是由天线的铜耗、介质损耗、加载元件的损耗以及接地损耗等造成的
假设这一部分功率为一电阻所吸收,称此电阻为损耗电阻,记为$R_{loss}$,则:
式中$I_A$式天线上某点的电流,则$R_{loss}$是归算于此电流的损耗电阻
若天线阻抗为$R_{\sum}$,上式也可表示为:
2.2 天线方向图
天线的方向性是指天线向一定方向辐射电磁波的能力。对于接收天线而言,方向性表示天线对不同方向传来的电磁波具有不同的接收能力。天线的方向性通常用方向图来表示
如果把天线在各方向辐射的强度用从原点出发的矢量来表示,则连接全部矢量端点所形成的曲面就是天线的方向图
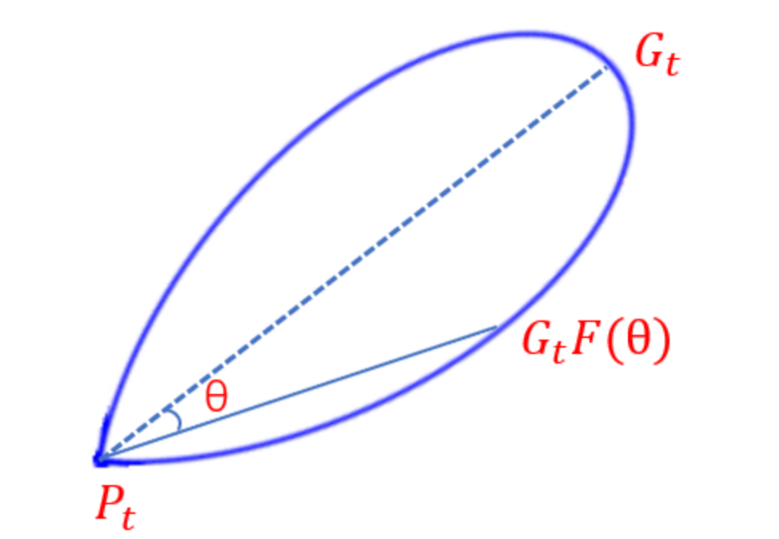
$P_t$:发射机功率
$G_t$:最大增益(天线在最大辐射方向上辐射的功率$P_{max}$或$|E_{max}|^2$和无方向性天线(电源)的辐射功率$P_0$或$|E_0|^2$之比称为此天线的方向系数)
$G_tF(\theta)$:与最大增益方向夹角为$\theta$的方向对应的增益
天线方向图实际在360°方向都有值,与最大增益方向夹角越大,增益越小(只在主瓣范围内有效)
主瓣获得的功率增益,是以牺牲副瓣增益得到的
在方向图(又称波瓣图)中,包含所需最大辐射方向的辐射波瓣叫天线主波瓣,也称天线波束。主瓣之外的波瓣叫副瓣或旁瓣、边瓣,主瓣相反方向上的旁瓣叫后瓣、尾瓣
- 直角坐标系表示的方向图
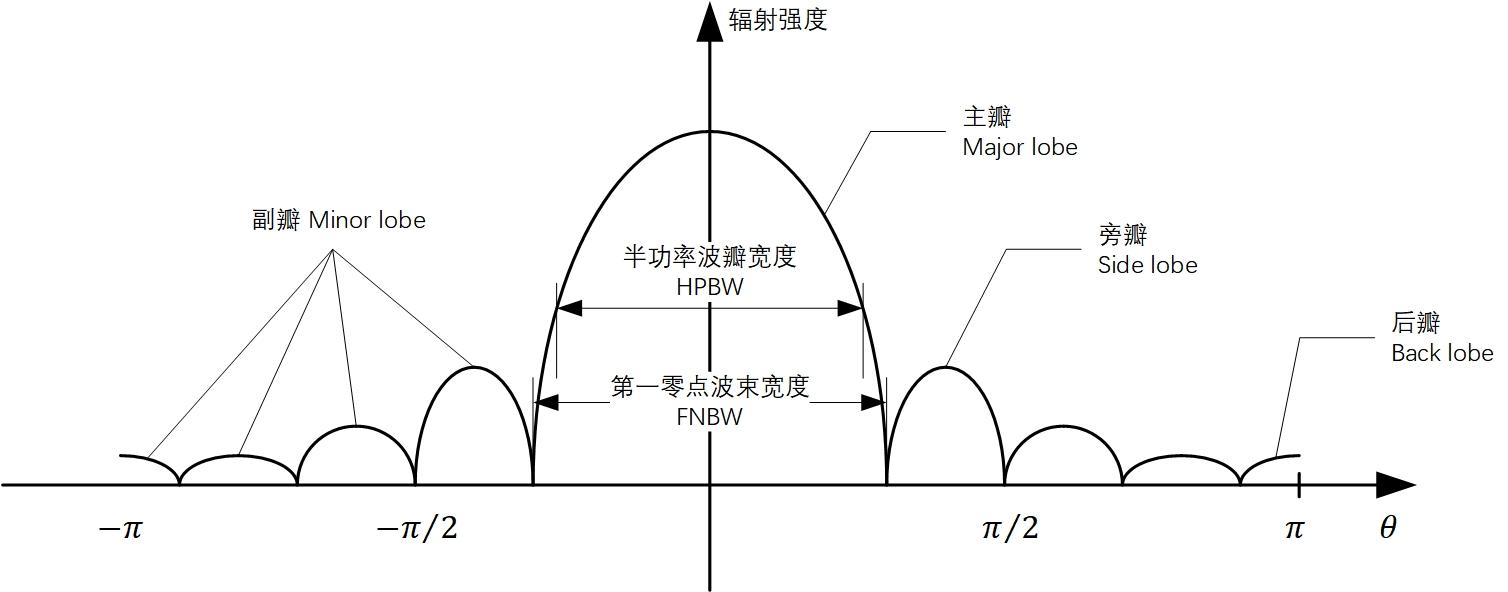
极坐标系表示的方向图
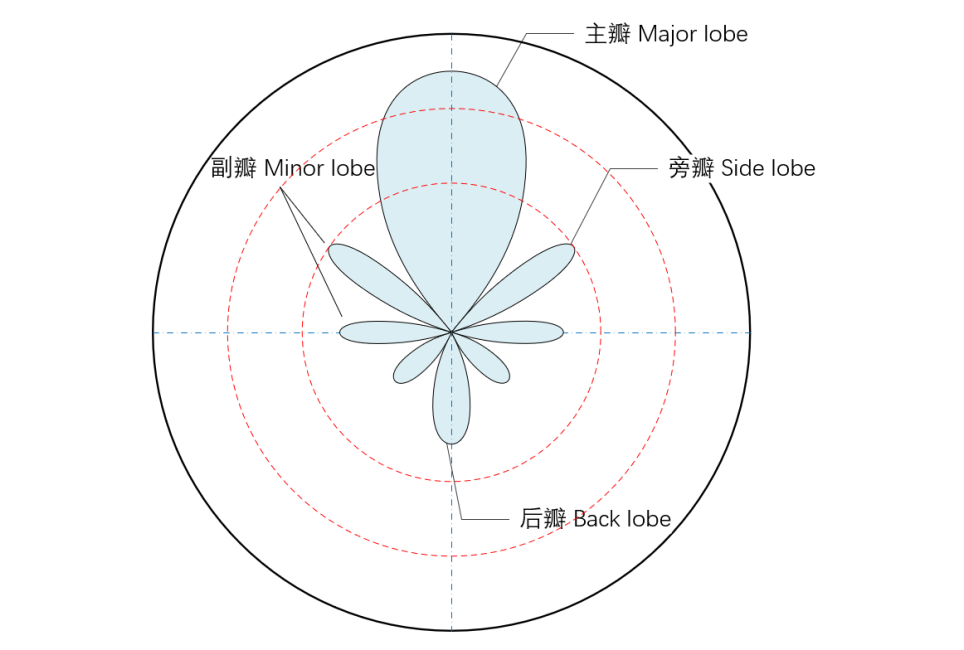
球坐标系表示的3D方向图
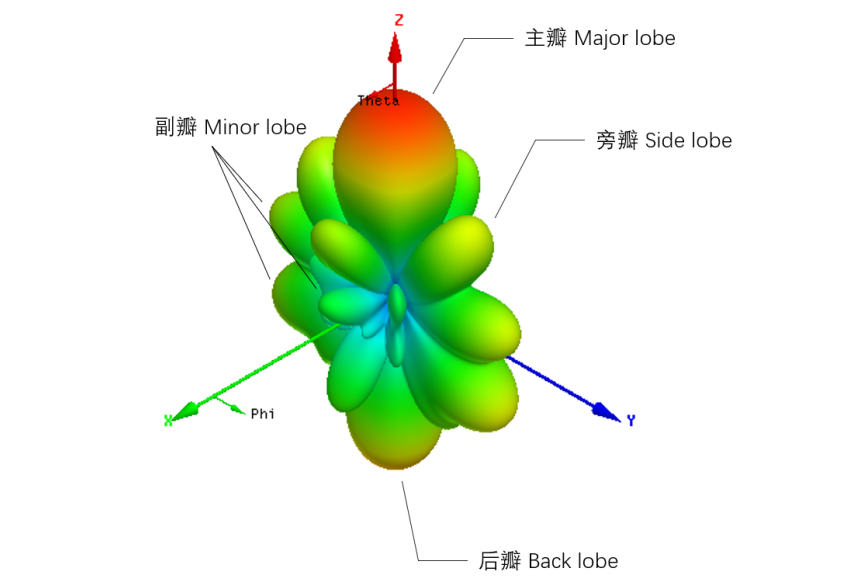
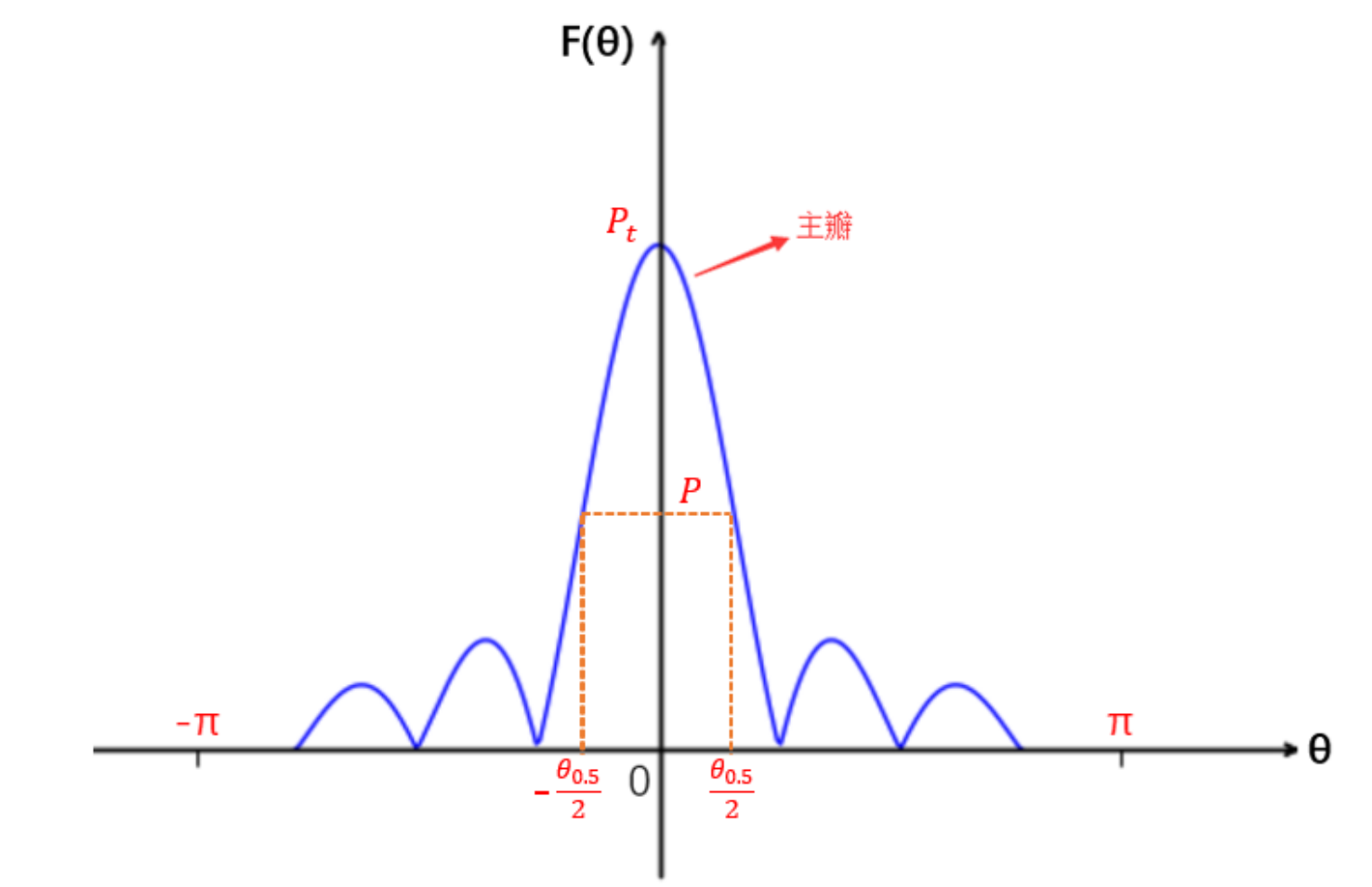
2.3 波束宽度
主瓣的宽度称为波束宽度,是衡量天线方向图胖瘦的指标
定义为主瓣功率下降到波束中央 1/2 功率处的宽度
波束宽度用$\theta_{3dB}$或者$\theta_{0.5}$表示
雷达的工作频率
常用的工作频率:220MHz~35GHz
又分为若干个波段:
| 波段名称 | 频率 |
| ————- | ——————- |
| L | 1000~2000MHz |
| S | 2000~4000MHz |
| C | 4000~8000MHz |
| X | 8000~12000MHz |
| K$\mu$ | 1.2~18GHz |
| K | 18~27GHZ |
| K$\alpha$ | 27~40GHz |
相关单位换算
- 1000yd=3000ft=0.914km≈0.6mile
- 1海里=1.853km
| $K$ | $M$ | $G$ | $m$ | $\mu$ | $n$ | $p$ |
|---|---|---|---|---|---|---|
| $10^3$ | $10^6$ | $10^9$ | $10^{-3}$ | $10^{-6}$ | $10^{-9}$ | $10^{-12}$ |
