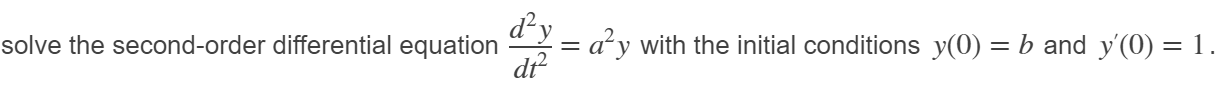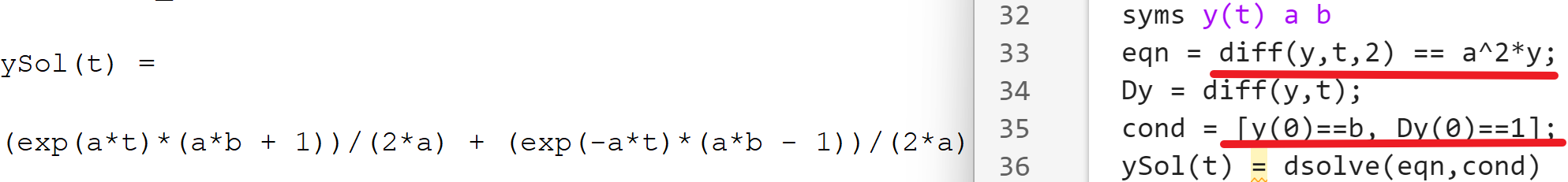本节主要介绍了MATLAB中符号对象的建立与相关运算,包括微积分、级数、方程求解。
符号对象
1.符号对象的建立
符合对象名=sym(A)A可以是一个数值常量、数值矩阵或数值表达式,此时符号对象是一个符号常量
A也可以是一个变量名,这时符号对象为一个符号变量
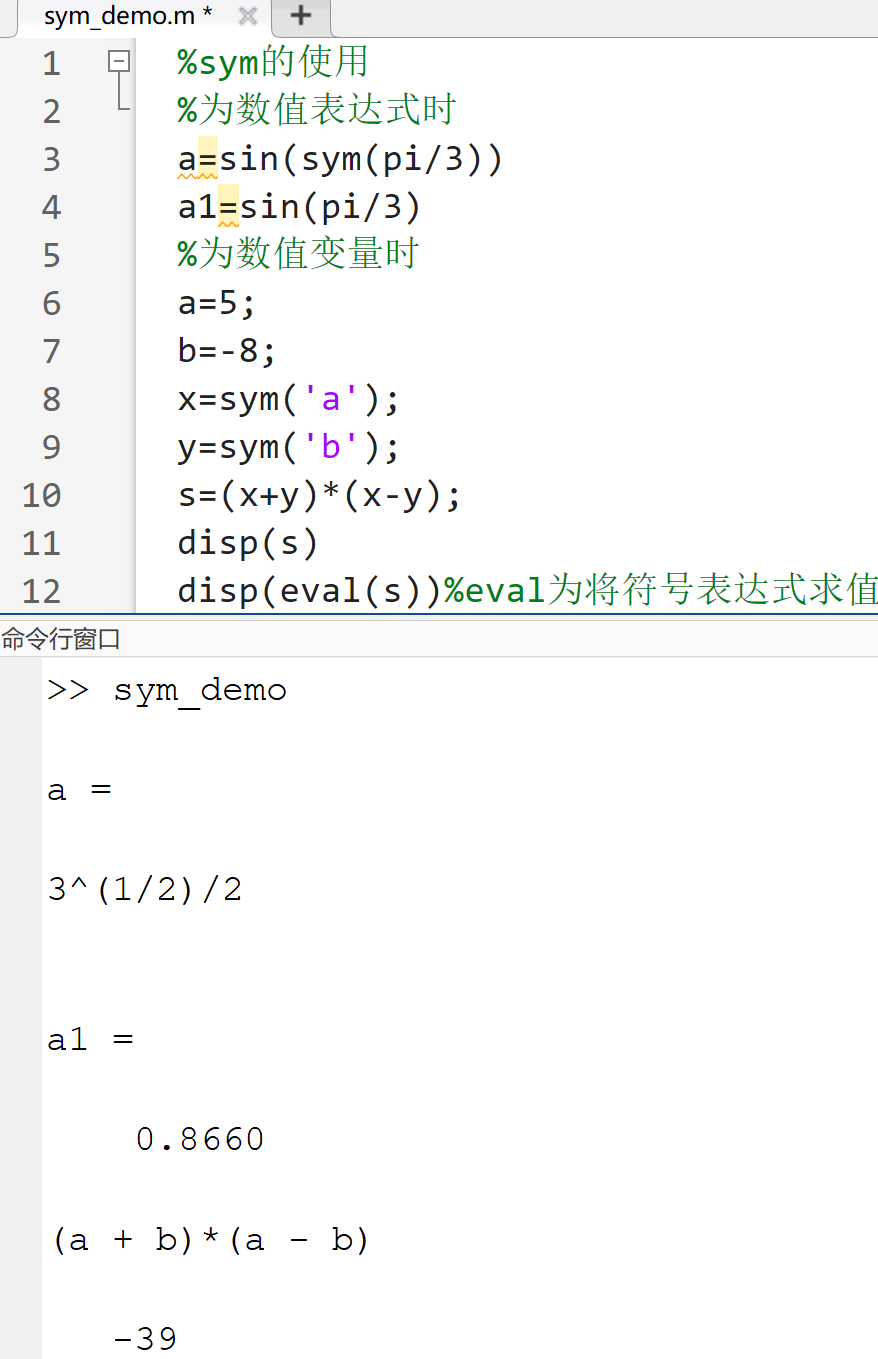
- 由结果可以看出符号计算的结果是一个精确的数学表达式,数值计算的结果是一个数值
syms 符号变量名1 符号变量名2 …… 符号变量名n%一次定义多个符号变量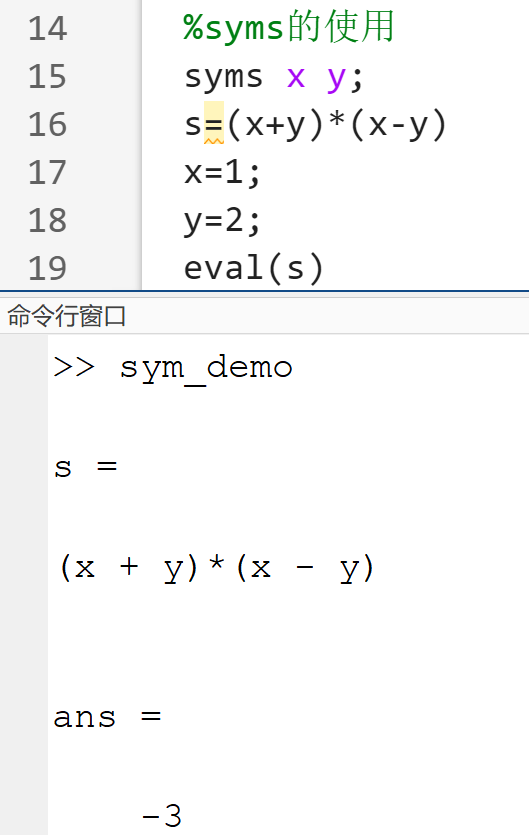
2.符号对象的运算
四则运算:
+、-、*、/、^,符号运算结果依然是一个符号表达式关系运算符:
<、<=、>、>=、==、~=使用assume函数对符号对象设置值域
assume(condition)%指定变量满足条件conditionassume(expr,set)%指定表达式expr属于集合set
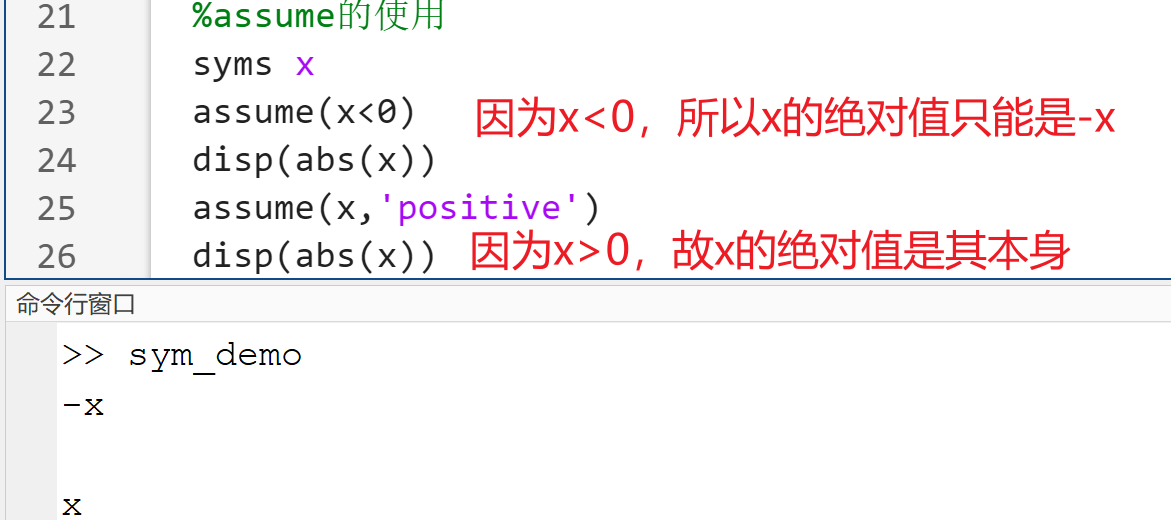
逻辑运算:
&、|、~因式分解与展开运算:
factor(s):对符号表达式s分解因式expand(s):对符号表达式s进行展开collect(s):对符号表达式s合并同类项
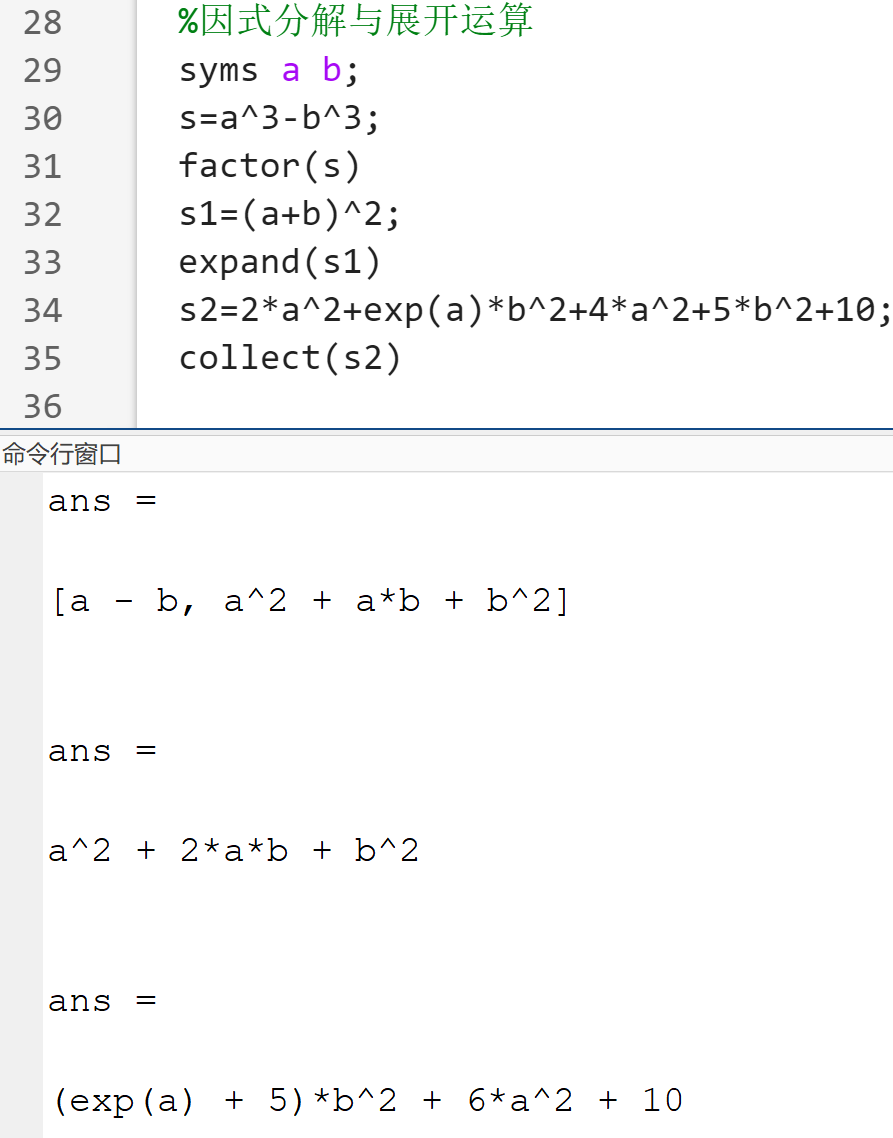
其他运算
- 提取有理分式的分子分母:
[n,d]=numden(s) - 提取符号表达式的系数:
c=coeffs(s,x) - 符号表达式化简:
simplify(s) - 符号多项式与多项式系数向量之间的转换
- 符号多项式转换为多项式系数向量:
p=sym2poly(s)%其中符号表达式s只能有一个符号变量 - 多项式系数向量转化为符号多项式:
s=poly2sym(p)
- 符号多项式转换为多项式系数向量:
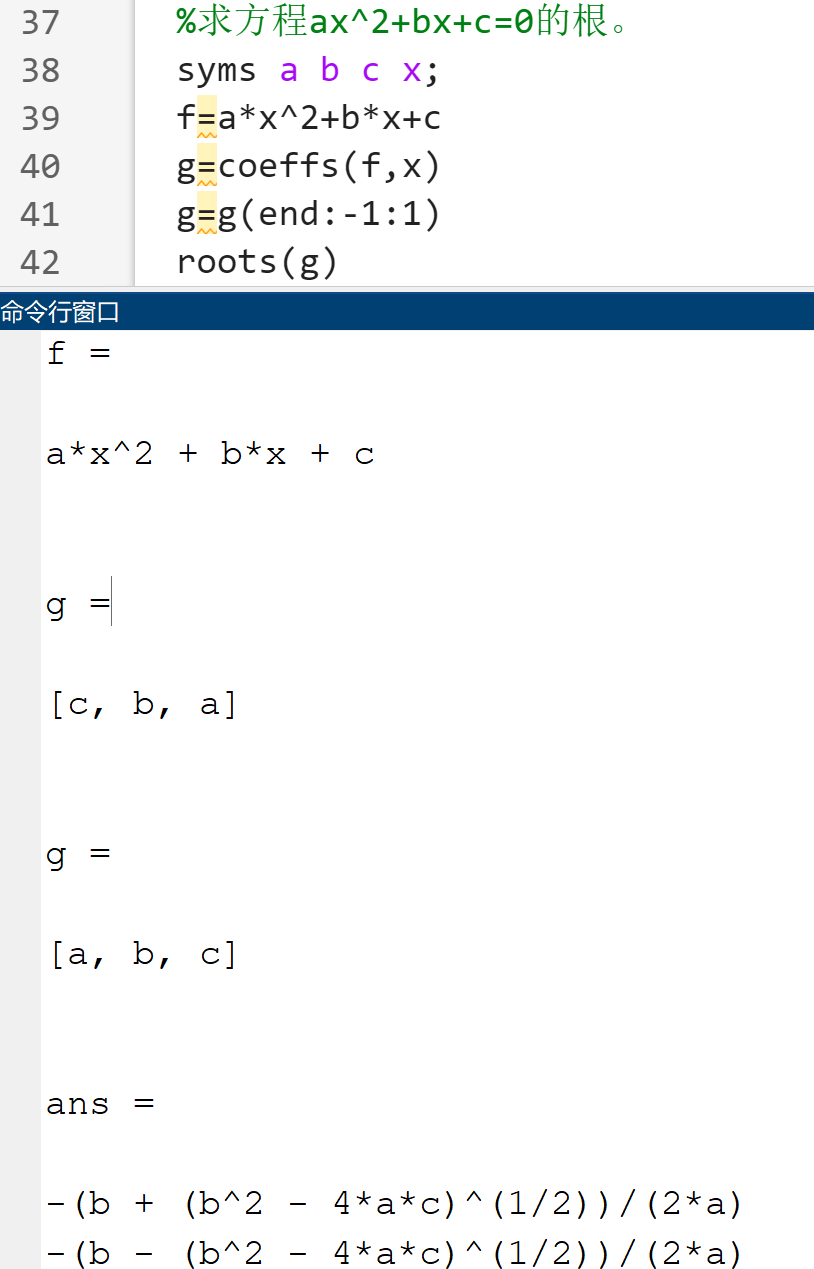
- 提取有理分式的分子分母:
符号微积分
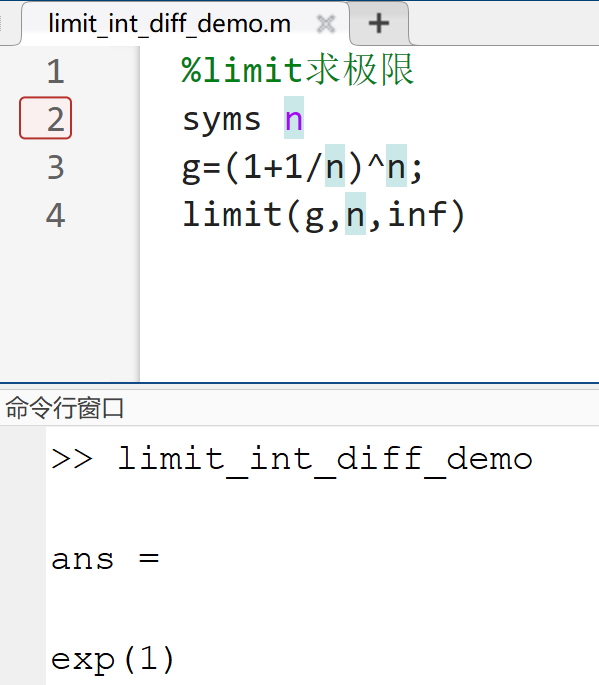
1.符号函数的极限
limit(f,x,a)%求函数f关于变量x在a点的极限
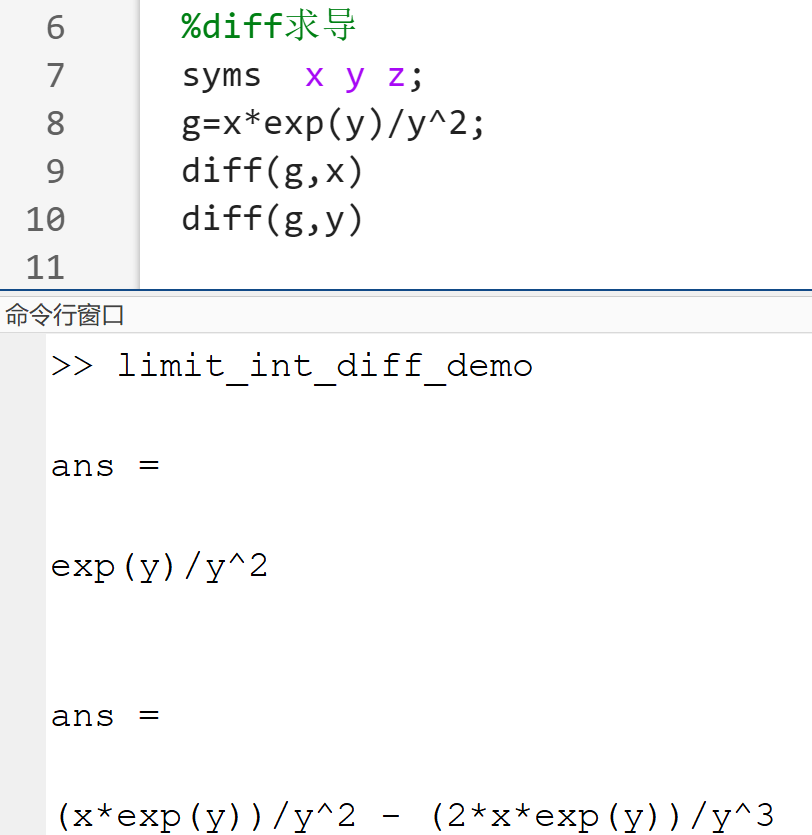
2.符号函数的导数
diff(f,x,n)%求函数f关于变量x的n阶导数,n的默认值是1
3.符号函数的积分
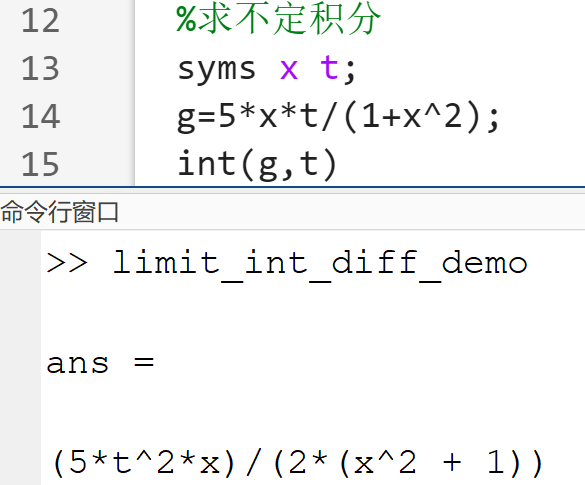
不定积分
int(f,x)%即求函数f对变量x的不定积分
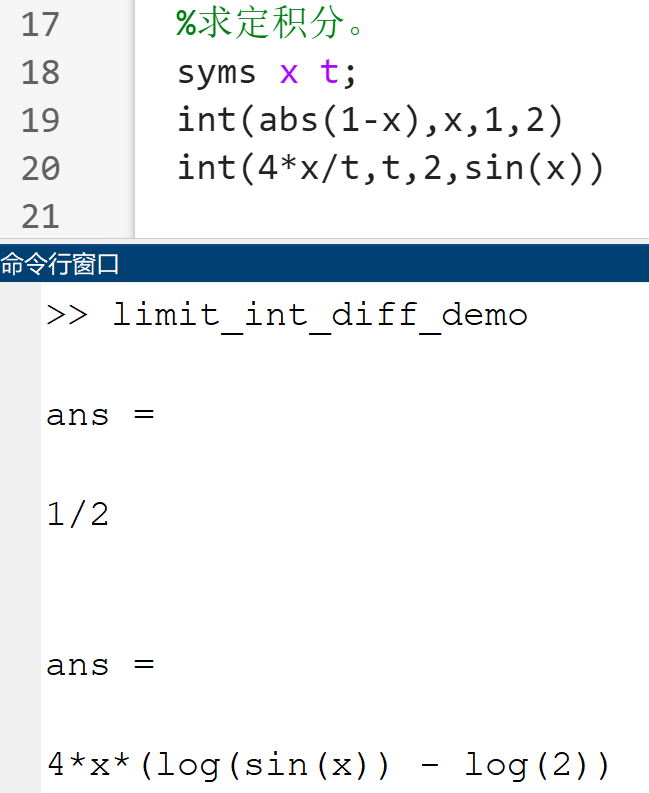
定积分
int(f,x,a,b)- a,b分别表示定积分的下限和上限
- a,b中有一个符号表达式时,函数返回一个符号函数
级数
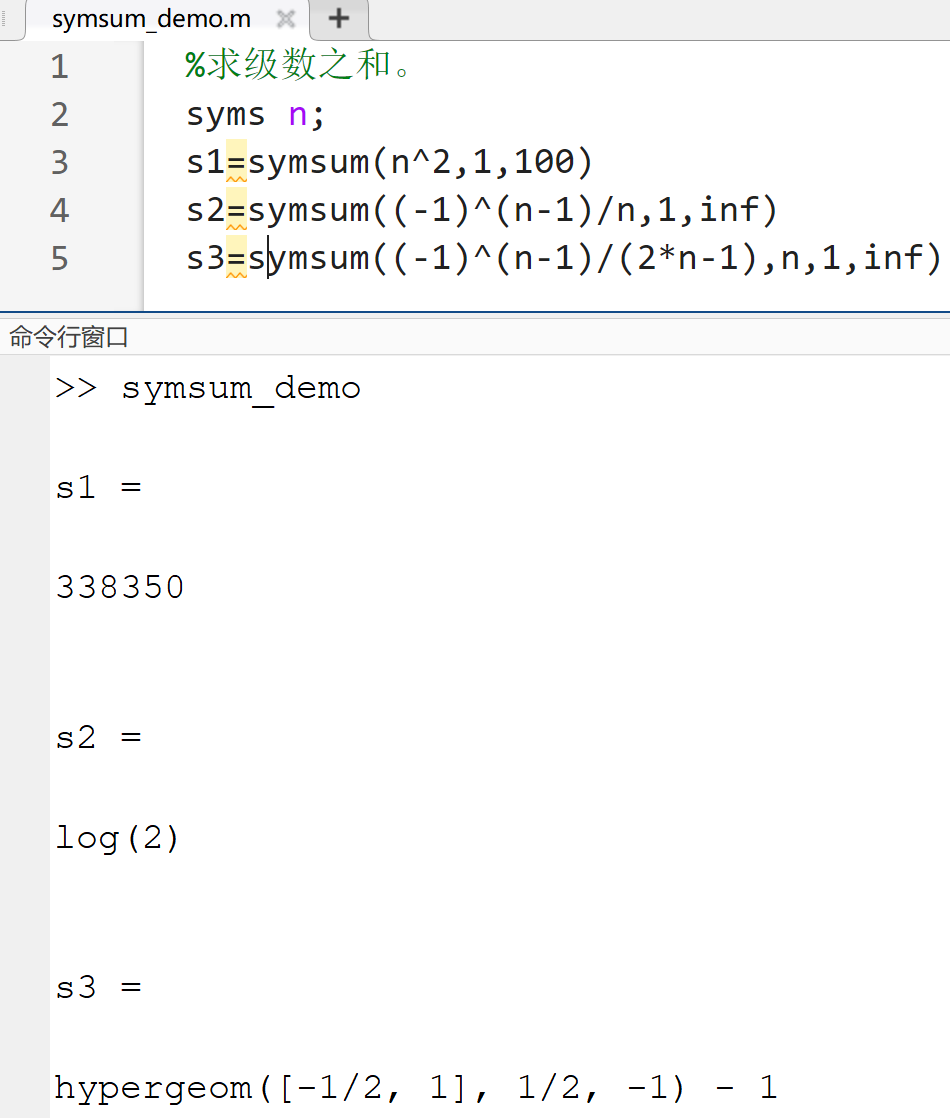
1.级数求和
symsum(s,v,n,m)- s表示一个级数的通项,是一个符号表达式
- v是求和变量
- n、m时是求和变量v的初值和末值
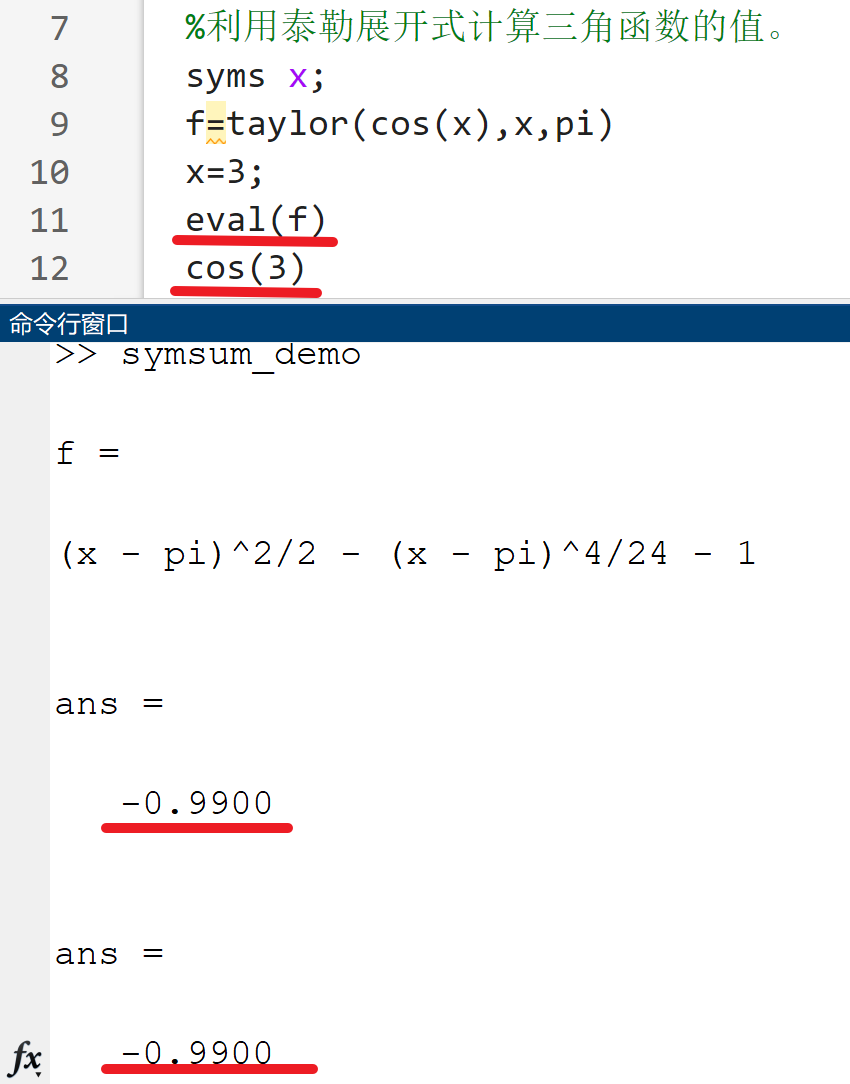
2.泰勒级数
taylor(f,v,a,Name,Value)函数f按变量v在a点展开为泰勒级数
Name为选项名,Value为选项值
| Name | Value |
| ———————— | ———————————————————————————— |
| ‘ExpansionPoint’ | 指定展开点,默认为0 |
| ‘Order’ | 指定截断参数,默认为6,即展开式的最高阶为5 |
| ‘OrderMode’ | 指定展开式采用绝对阶’Absolute’(默认)或相对阶’Relative’ |
符号方程求解
1.代数方程符号求解
solve(s,v)%求解符号表达式s的代数方程,求解变量为v
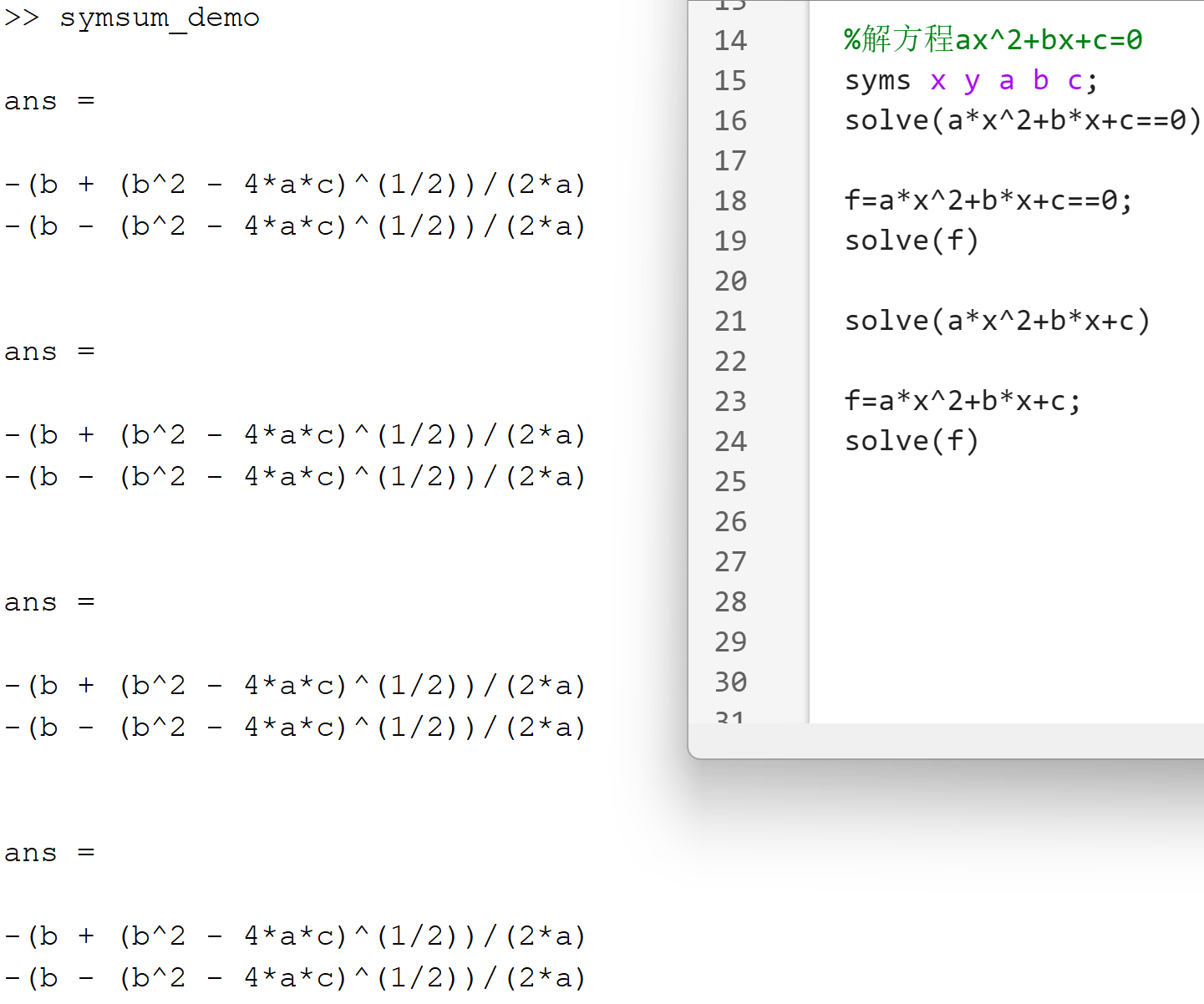
- solve函数求解方程不一定准确
2.常微分方程符号求解
dsolve(e,c,v)- e是常微分方程,导数用diff函数表示
- v是方程中的自变量
- 若没有给出初始条件c,则求方程的通解
例1:

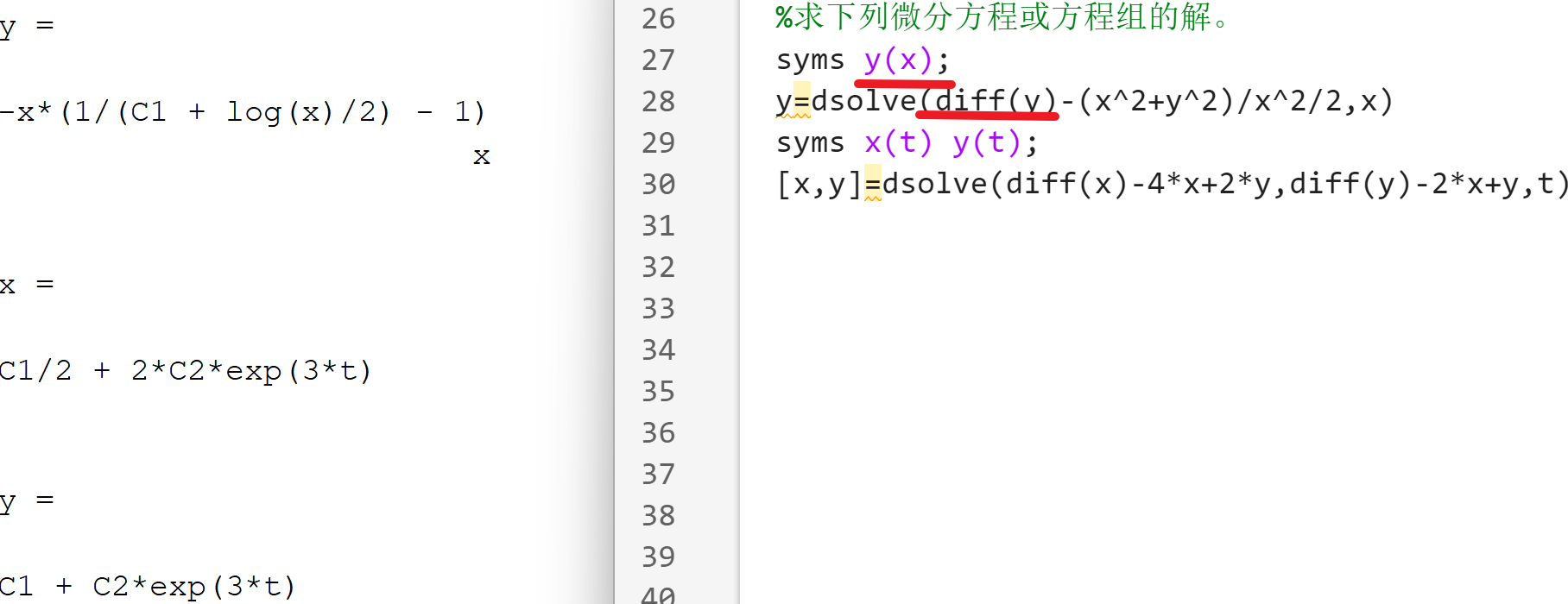
例2: