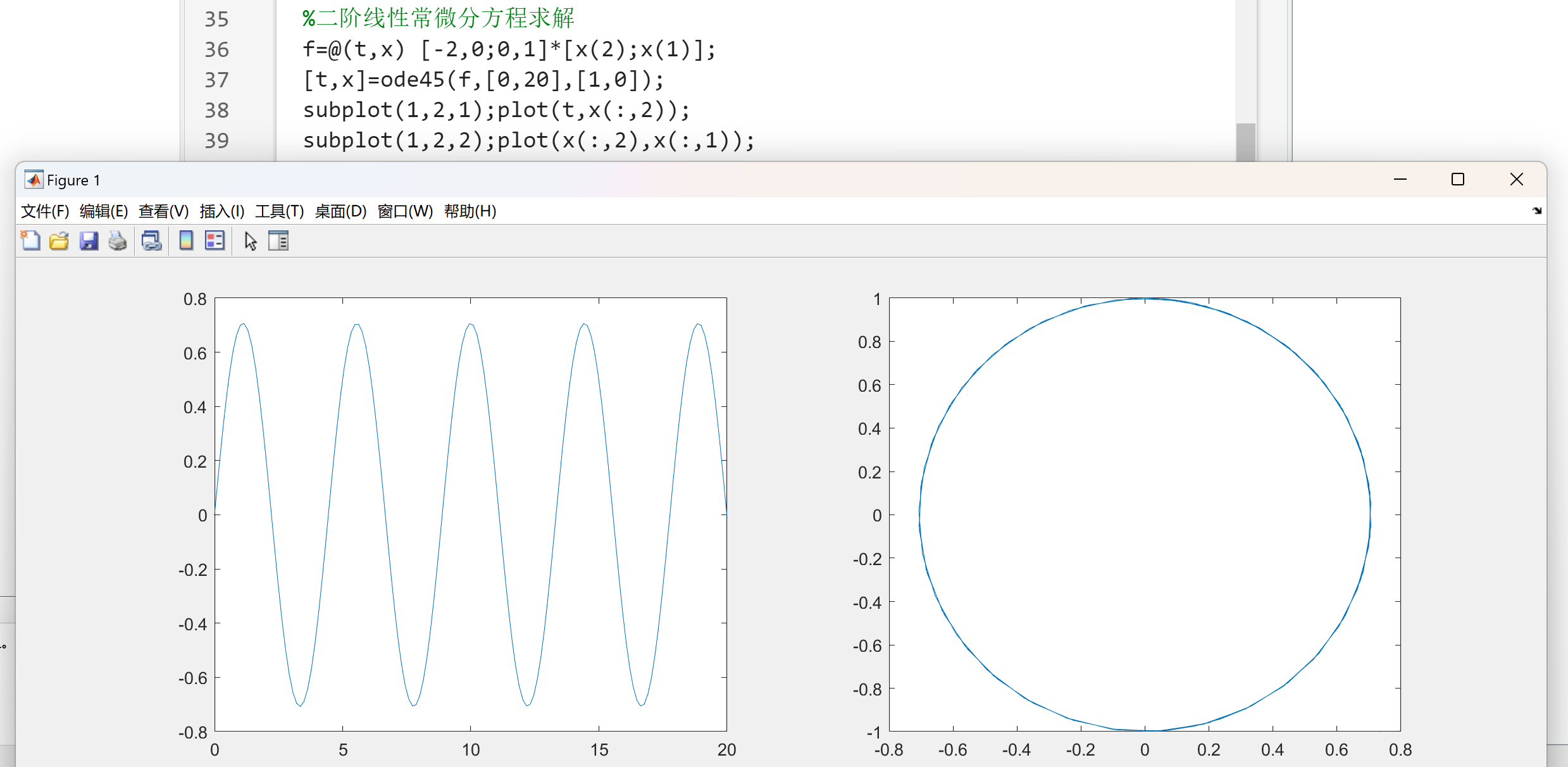
本节主要介绍了MATLAB中微积分的计算、线性方程与非线性方程的求解方法、以及常微分方程的求解。
数值微分与数值积分
1.数值微分的定义
函数在x0点处以h(h>0)为步长的差分公式:
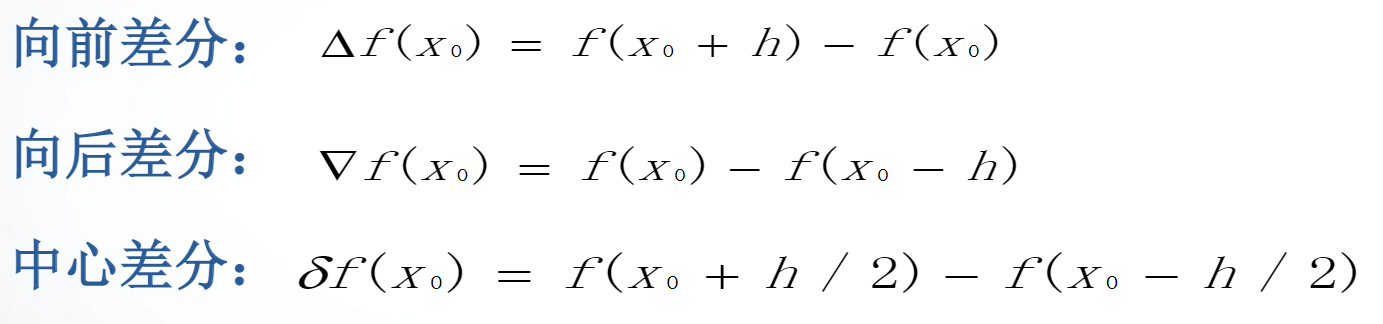
当步长h充分小时,得到 MATLAB之图像绘制.md 函数在x0点处以h(h>0)为步长的差商公式:
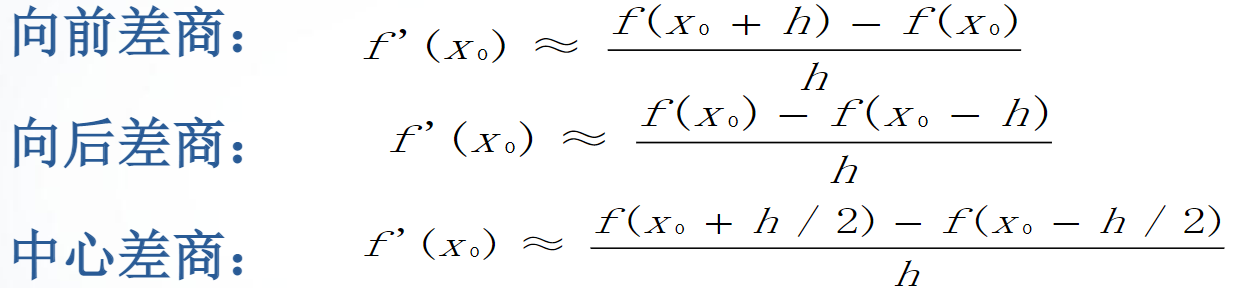
函数f(x)在点x0的微分接近于函数在该点的差分,而f在点x的导数接近于函数在该点的差商
2.数值微分的实现
dx=diff(x)%计算向量x的向前差分,dx(i)=x(i+1)-x(i)- 如果x是长度为 m 的向量,则 dx = diff(x) 返回长度为 m-1 的向量。dx的元素是x相邻元素之间的差分。
- dx = [X(2)-X(1) X(3)-X(2) … X(m)-X(m-1)]
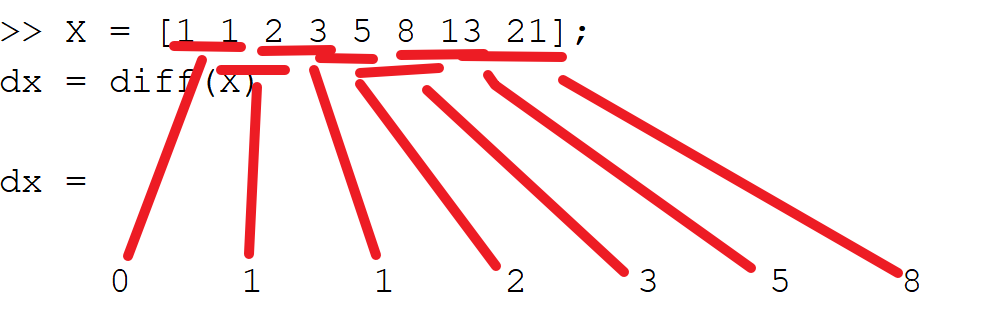
dx=diff(x,n)%计算向量x的n阶向前差分,相当于将diff(x)重复调用了n次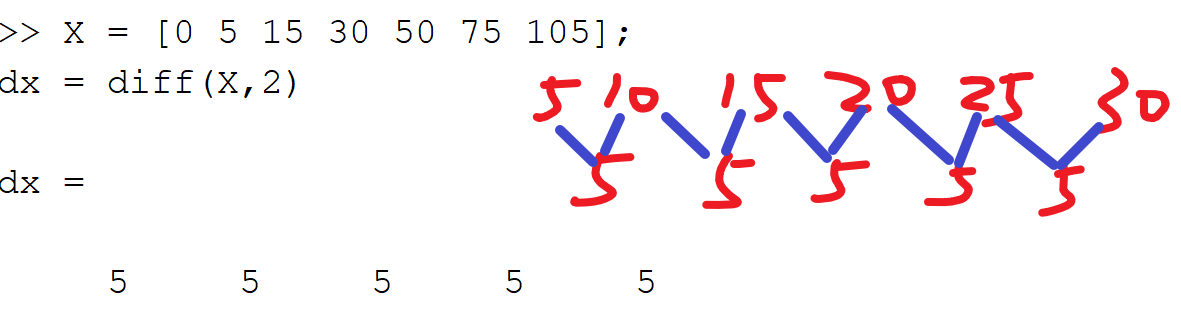
dx=diff(A,n,dim)%计算矩阵A的n阶差分
3.数值积分的定义
将积分区间[a,b]分成n个子区间[$x_i$,$x_{i+1}$],i=1,2,……,n,其中$x_1$=a;$x_{n+1}$=b,这样求定积分问题就分解为:
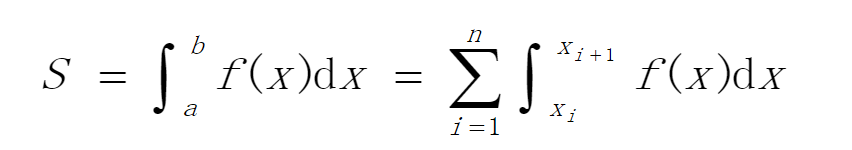
4.数值积分的实现
基于自适应辛普森方法
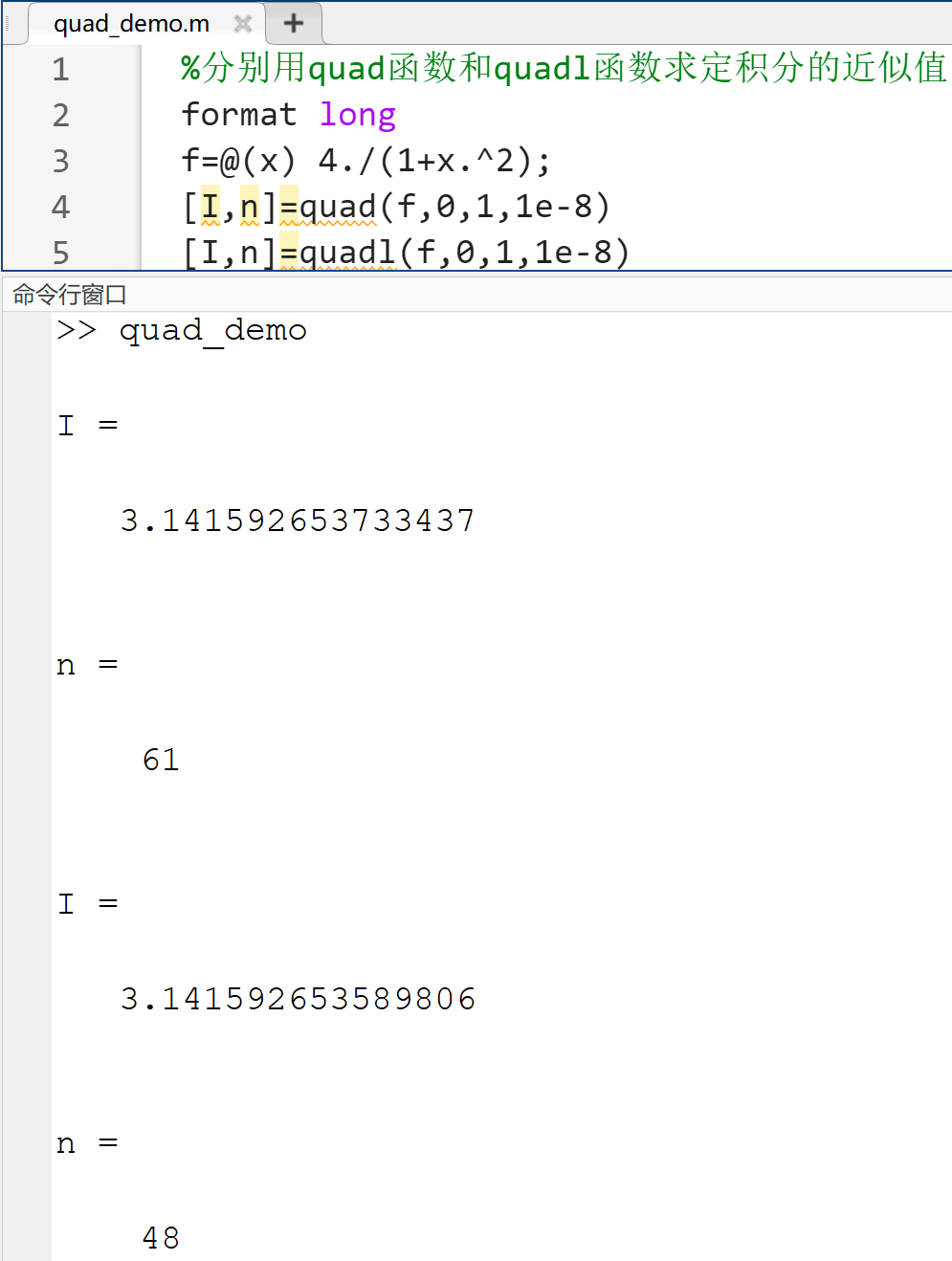
[I,n]=quad(filename,a,b,tol,trace)- tol用来控制绝对误差容限,默认取$10^{-6}$
- trace控制是否展现积分过程,取0则不展示(默认)
- 返回参数I即定积分的值,n为被积函数的调用次数
基于自适应Gauss-Lobatto方法
[I,n]=quadl(filename,a,b,tol,trace)
基于全局自适应积分方法(MATLAB推荐使用)
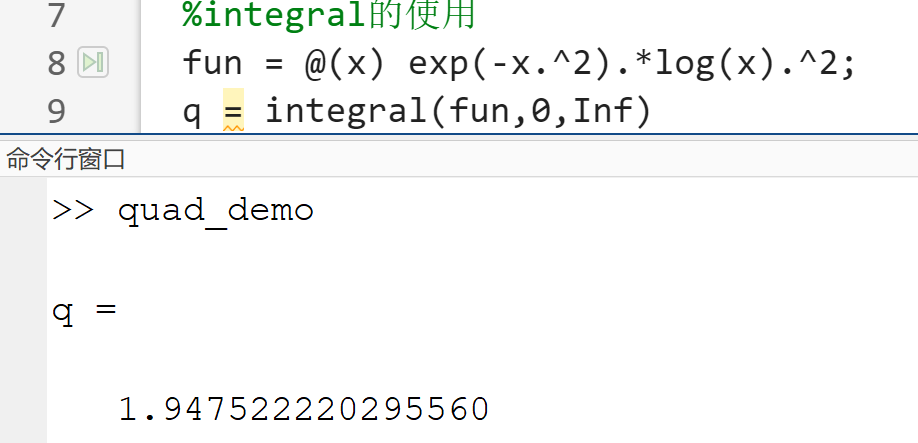
I=integral(filename,a,b)- I是计算得到的积分,filename是被积函数
- a和b分别是定积分的下限和上限
- 积分限可以为无穷大,
Inf表示无穷大
多重积分的数值求解
二重积分
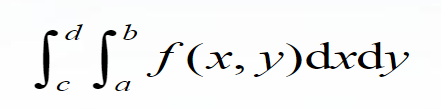
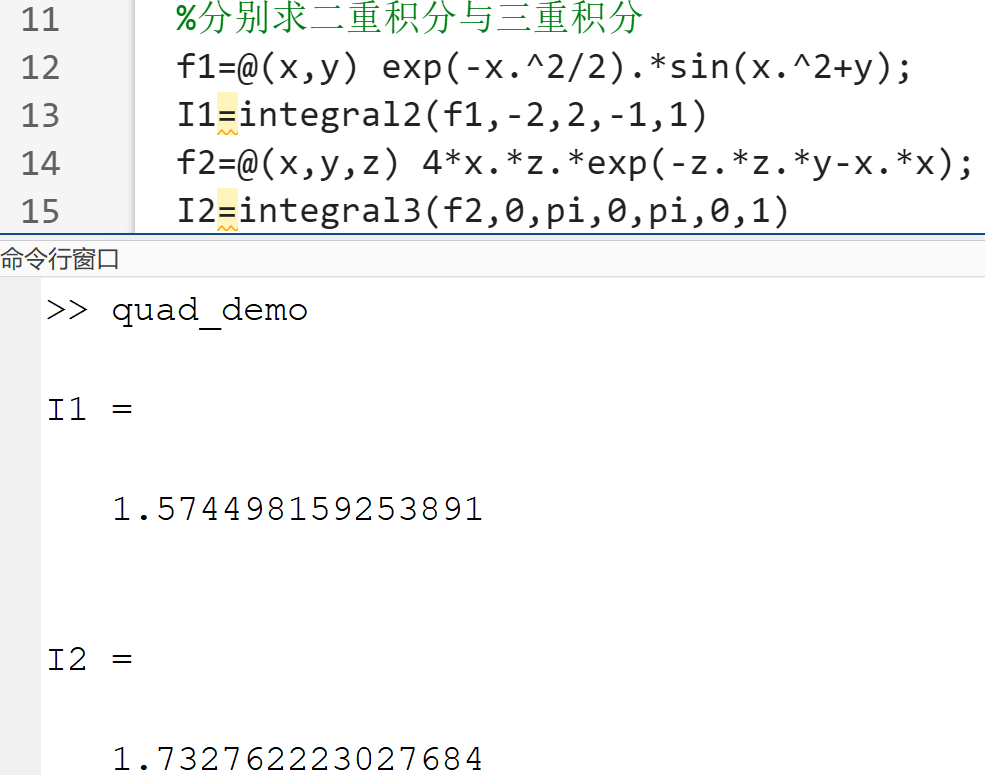
I=integral2(filename,a,b,c,d)I=quad2d(filename,a,b,c,d)I=dblquad(filename,a,b,c,d,tol)
三重积分
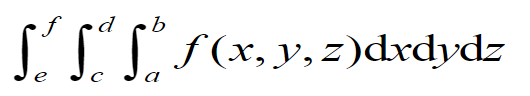
I=integral3(filename,a,b,c,d,e,f)I=triplequad(filename,a,b,c,d,e,f,tol)
线性方程组求解
1.直接法
利用左除运算符的直接解法
- Ax=b ———>
x=A\b
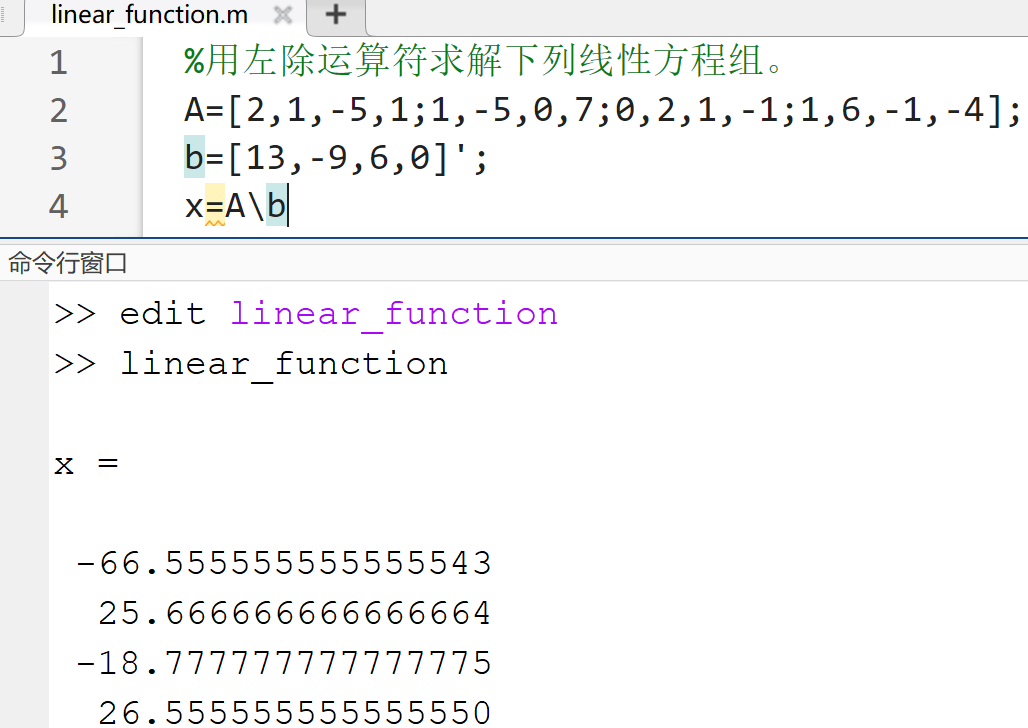
- Ax=b ———>
利用矩阵分解求解——LU解法
LU分解的基本思想:将一个n阶矩阵表示为一个下三角矩阵和一个上三角矩阵的乘积。可以首先求解向量y使Ly=b,再求解Ux=y
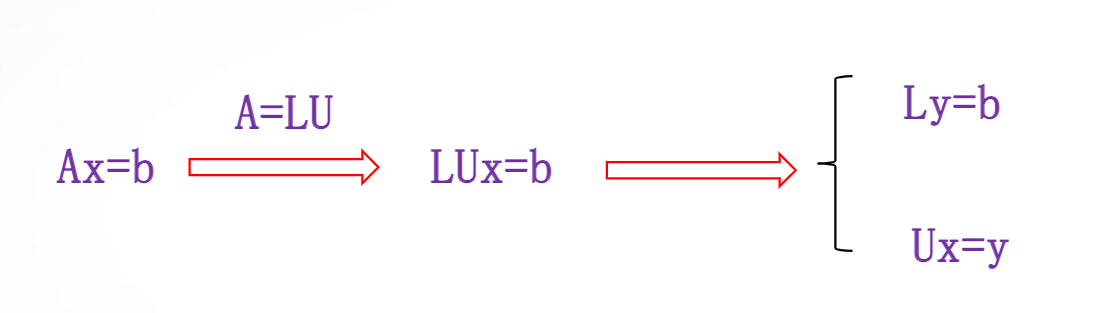
求解函数:
[L,U]=lu(A)%产生一个上三角阵U和一个变换形式的下三角阵L,使之满足A=LU,A必须是方阵[L,U,P]=lu(A)%PA=LU,A必须是方阵
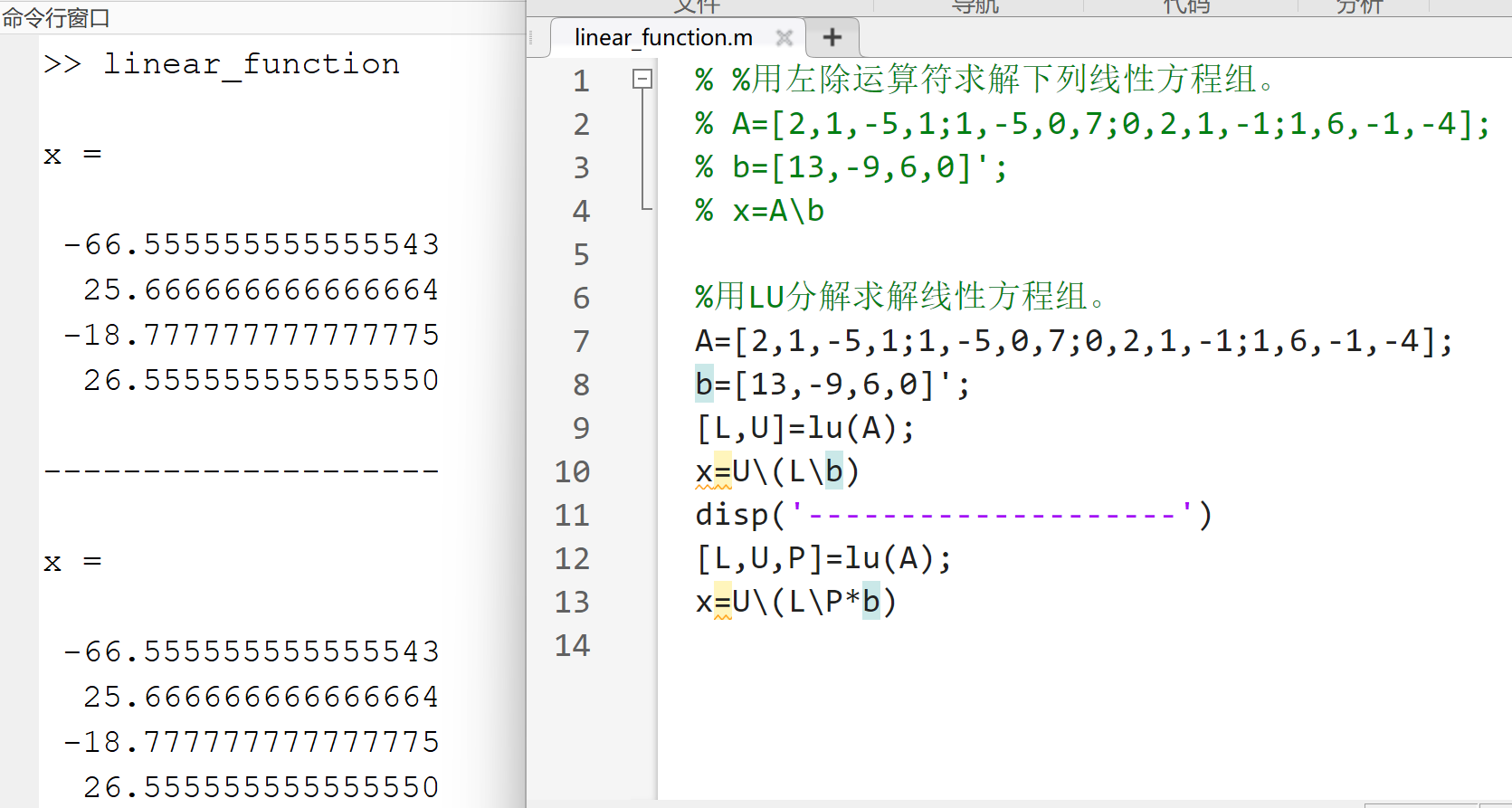
2.迭代法
雅可比(Jacobi)迭代法
基本思想:

函数编写
1
2
3
4
5
6
7
8
9
10
11
12
13
14%雅可比迭代法的函数文件jacobi.m:
function [y,n]=jacobi(A,b,x0,ep) %x0是初值,ep是误差
D=diag(diag(A));
L=-tril(A,-1);
U=-triu(A,1);
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep
x0=y;
y=B*x0+f;
n=n+1;
end
高斯-赛德尔(Gauss-Serdel)迭代法
基本思想:
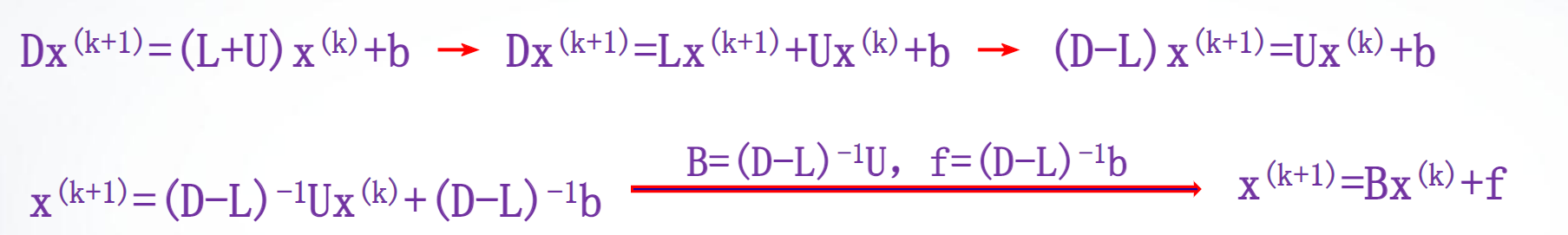
函数编写
1
2
3
4
5
6
7
8
9
10
11
12
13
14%Gauss-Serdel迭代法的函数文件
function [y,n]=gauseidel(A,b,x0,ep)
D=diag(diag(A));
L=-tril(A,-1);
U=-triu(A,1);
B=(D-L)\U;
f=(D-L)\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep
x0=y;
y=B*x0+f;
n=n+1;
end
调用:
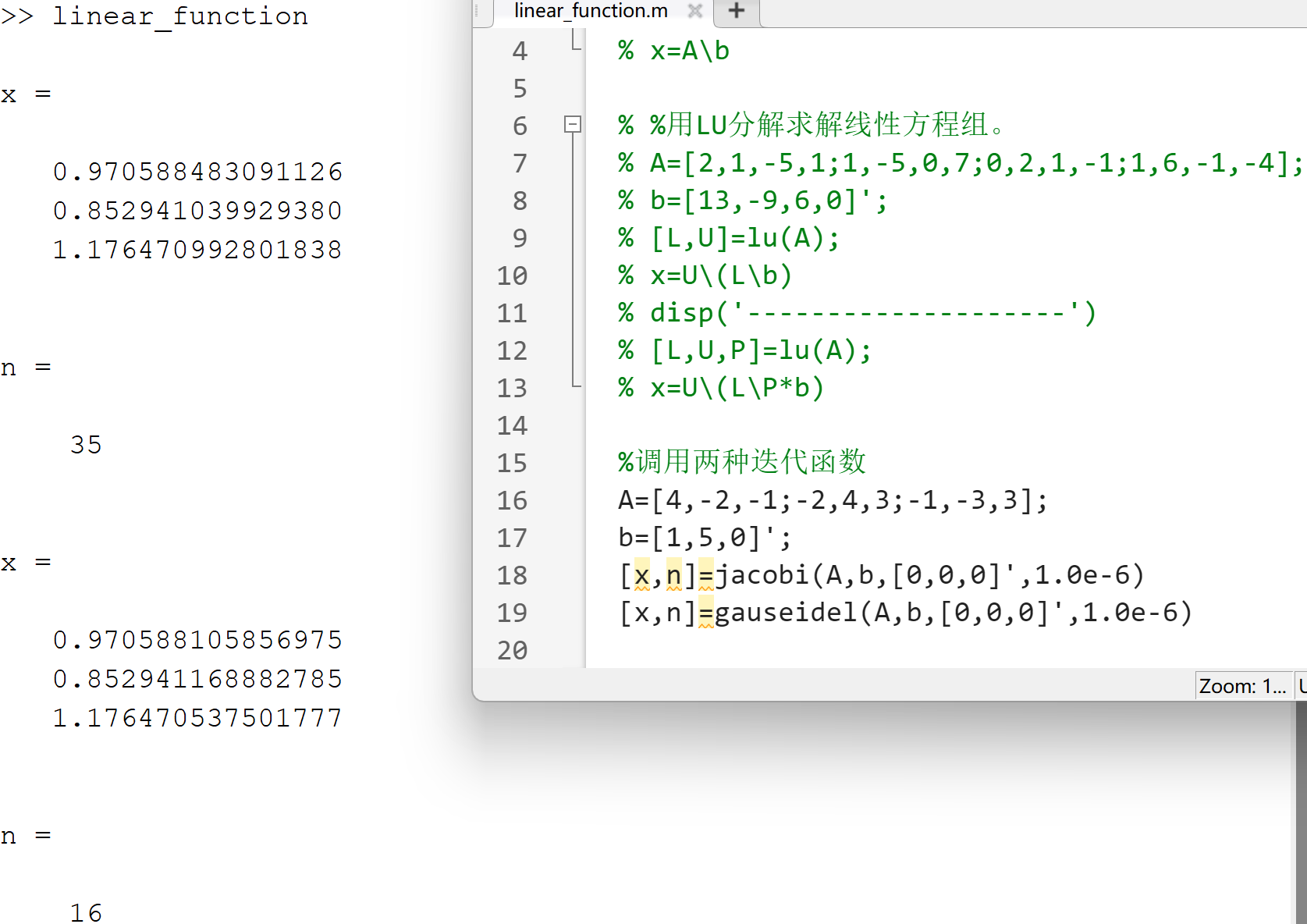
非线性方程求解与函数极值计算
1.非线性方程数值求解
单变量非线性方程求解
x=fzero(filename,x0)%x0是初值
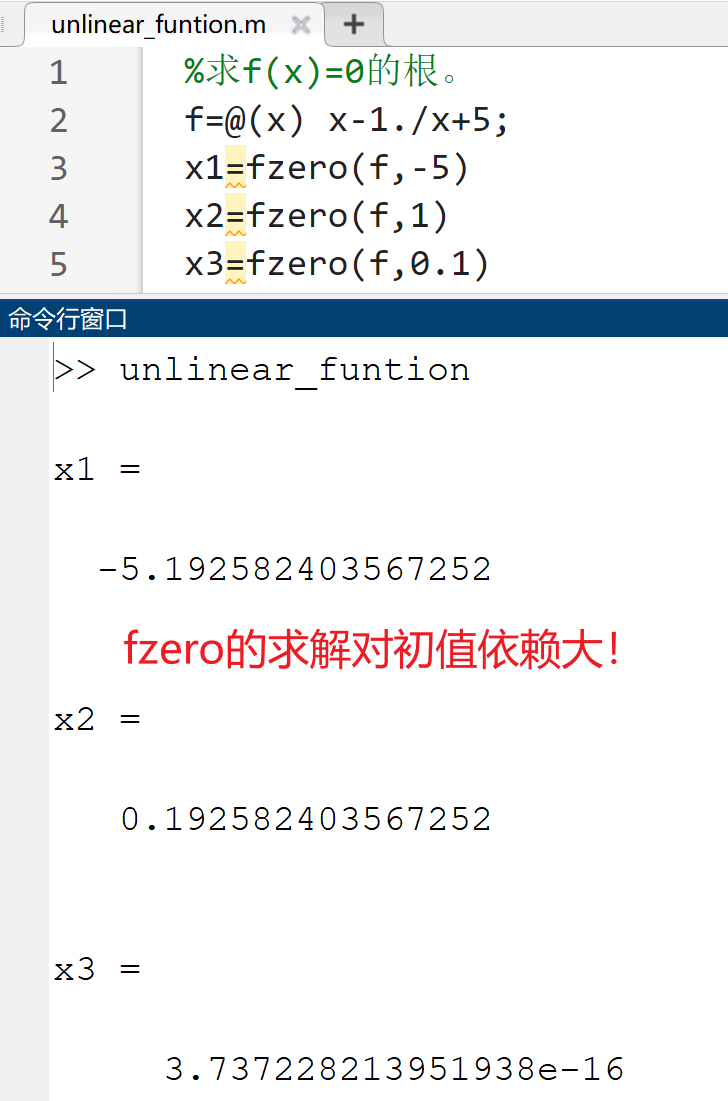
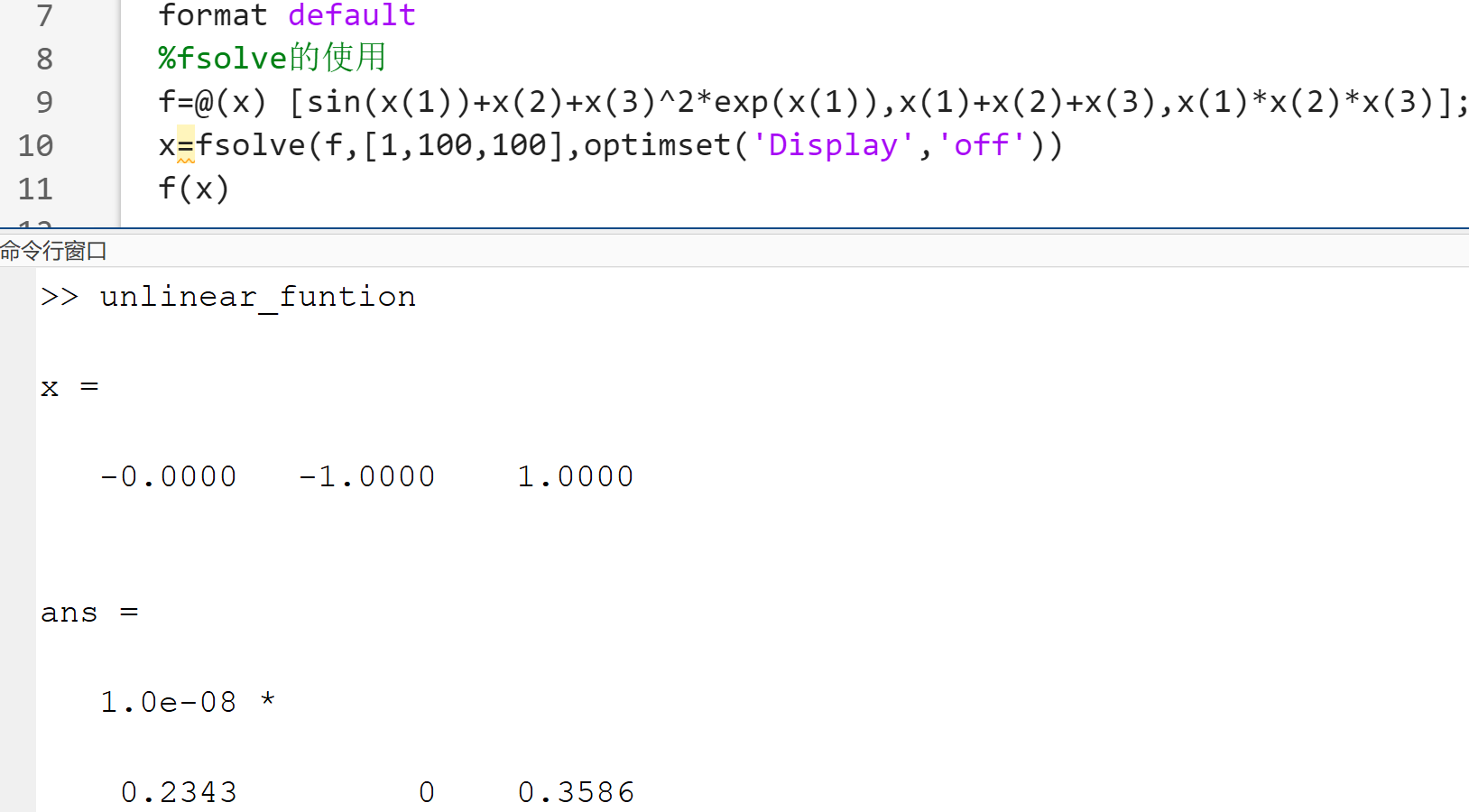
非线性方程组的求解
x=fsolve(filename,x0,option)- x为返回的解的近似解,x0是初值
- opton用于设置优化工具箱的优化参数,可以调用optimset函数来完成
2.函数极值的计算
无约束最优化问题
[xmin,fmin]=fminbnd(filename,x1,x2,option)[xmin,fmin]=fminsearch(filename,x0,option)[xmin,fmin]=fminunc(filename,x0,option)- x1、x2分别表示被研究区间的左、右边界;后两个函数的输入变量x0是一个向量,表示极值点的初值
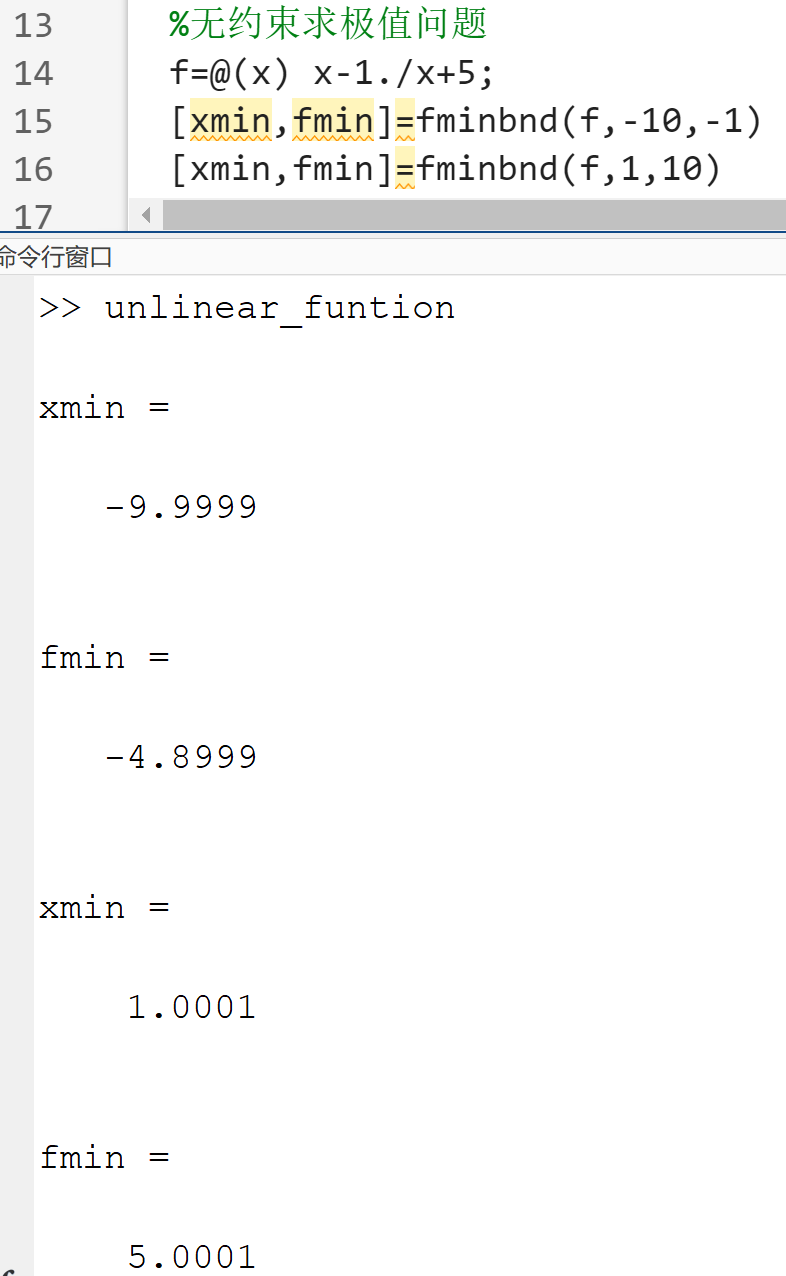
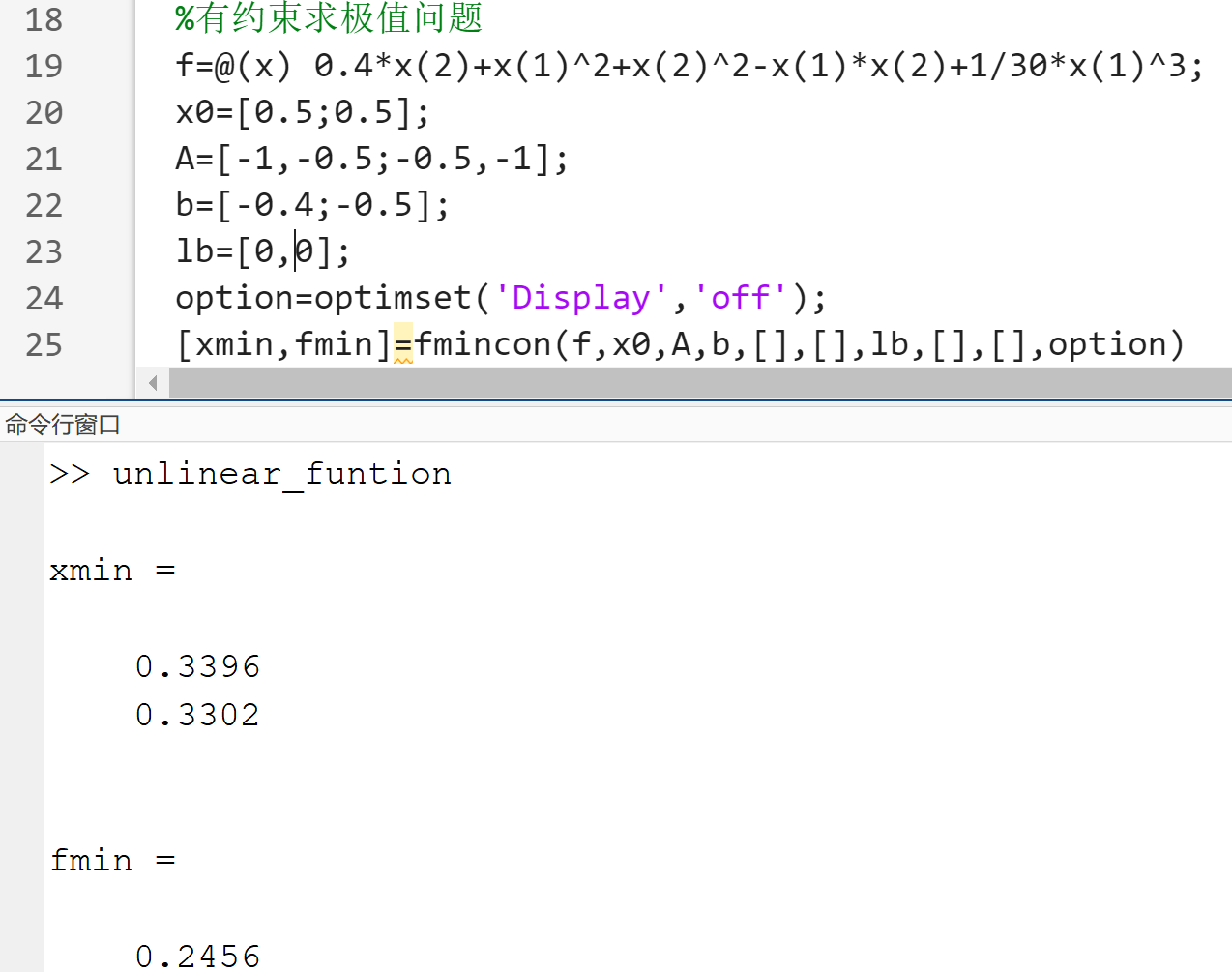
有约束最优化问题
[xmin,fmin]=fmincon(filename,x0,A,b,Aeq,beq,Lb,ub,nonlcon,options)其中的限制条件为:nonlcon为函数句柄,接受向量或数组 x,并返回两个数组 c(x) 和 ceq(x)。
c(x) 是由 x 处的非线性不等式约束组成的数组。
fmincon尝试满足对于 c 的所有项,有 c(x) <= 0。
ceq(x) 是 x 处的非线性等式约束的数组。fmincon 尝试满足
对于 ceq 的所有项,有 ceq(x) = 0。
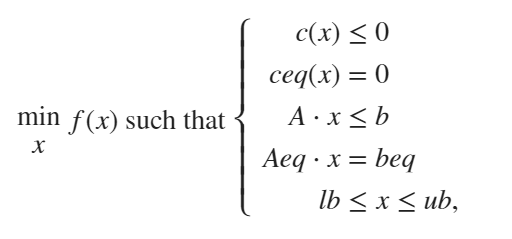
常微分方程数值求解
1.常微分方程数值求解的一般概念
- 求解常微分方程初值问题就是寻找函数y(t)使之满足如下方程

2.一般调用格式
[t,y]=solver(filename,tspan,y0,option)tspan为[t0,tf],表示求t在某一范围内的解
y0是初始状态向量
t,y分别给出时间向量和相应的数值解
solver的统一命名格式:
ode是常微分方程的英文缩写
nn代表所用方法的阶数
xx是字母,用于标注方法的专门特征
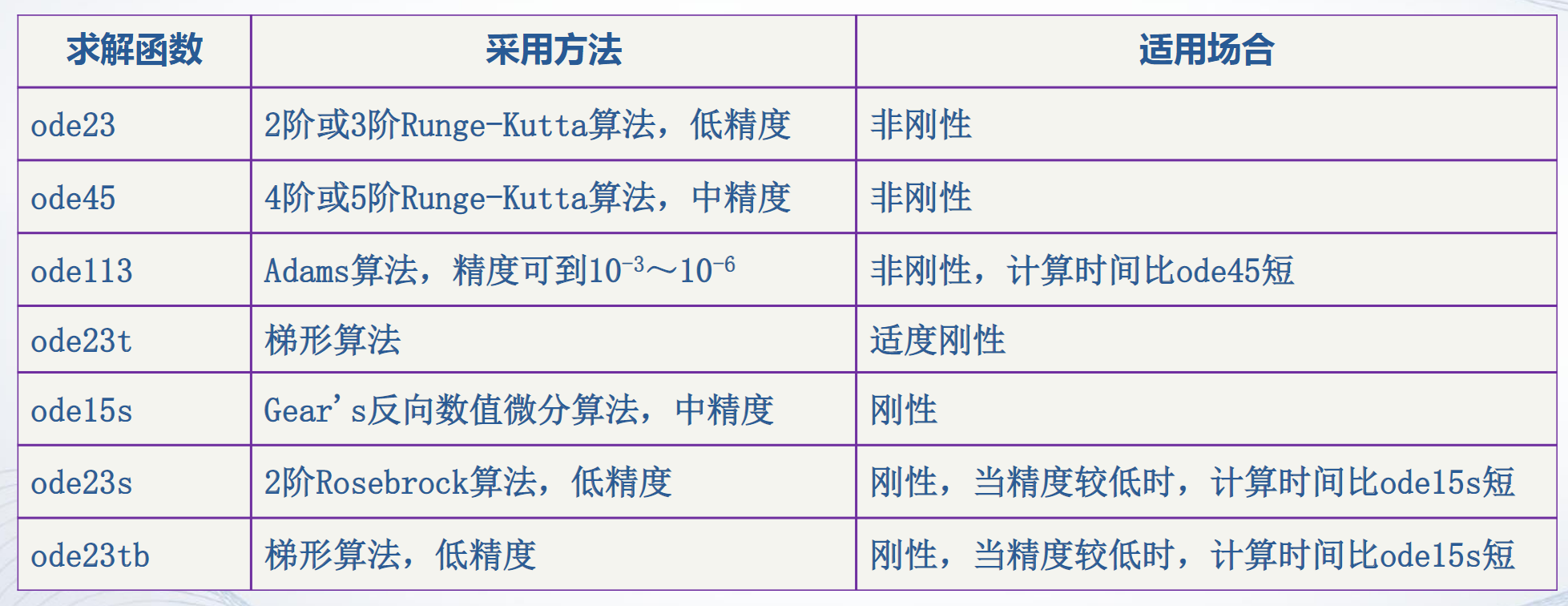
常用的求解函数:
3.相关实例
例1:

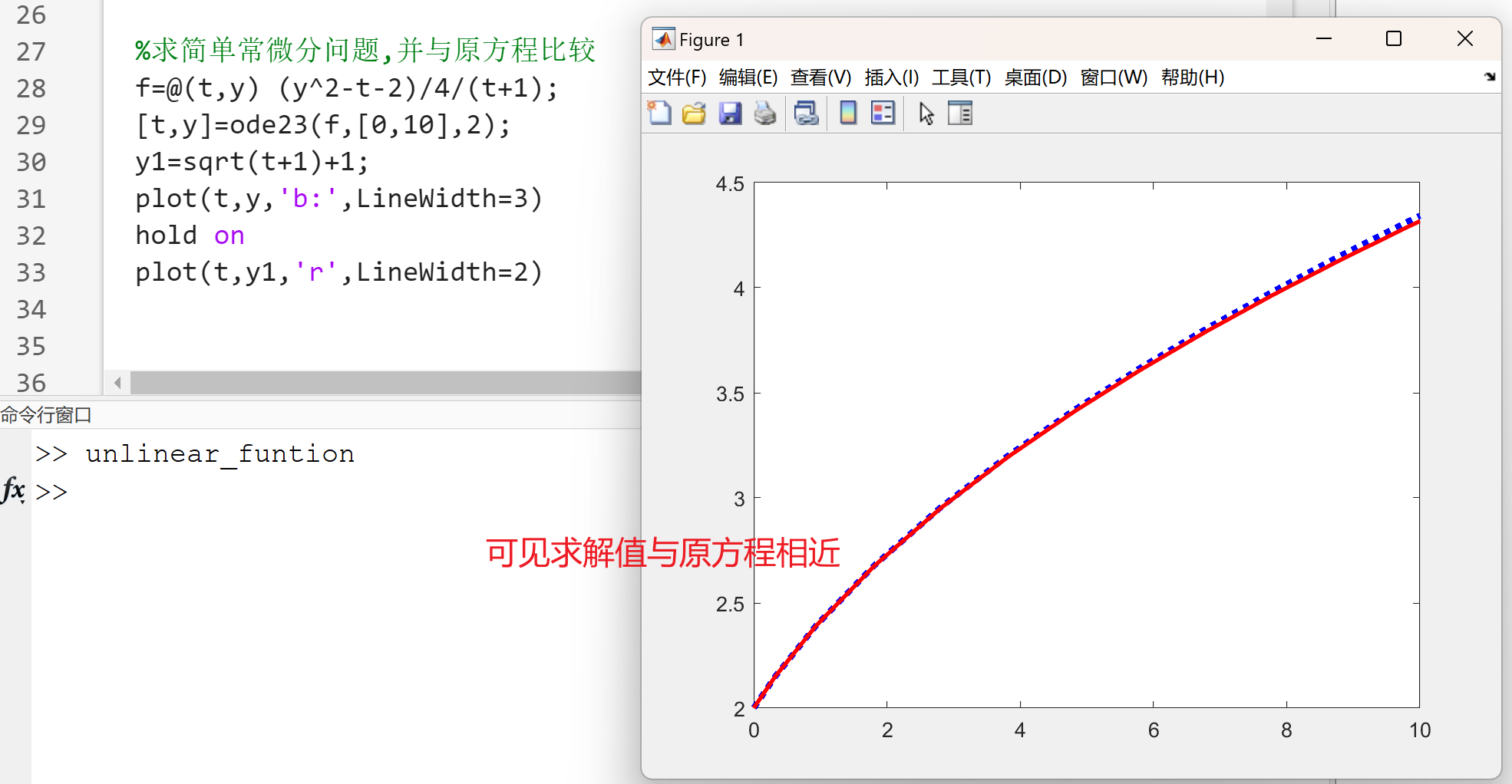
例2: