本节主要介绍了MATLAB中常用的统计分析函数、多项式相关计算以及数据插值与曲线拟合函数。
数据统计分析
1.最大值与最小值
- max() 与 min()
[y,k]=max(A,[],dim)%dim=1(默认值)时,求每列的最大值,并返回一个每列最大值下标的行向量;当dim=2时,求每行的最大值,并返回一个每行最大值小标的列向量;dim=‘all’即求全局最大值


2.平均值和中值
mean(A,dim)%求算术平均值median(A,dim)%求中值
3.和与求积
sum(A,dim)%求和函数prod(A,dim)%求积函数
4.累加和与累乘积
cumsum(A,dim)%累加和函数cumprod(A,dim)%累乘积函数

5.标准差与相关系数
std(A,flag,dim)%flag=0时,按S1所列公式计算样本标准方差;当flag=1时,按S2所列公式计算样本标准方差,在默认情况下,flag=0,dim=1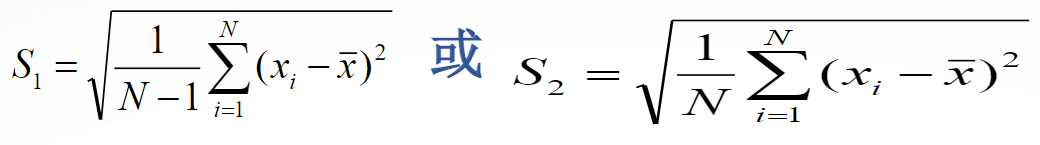
corrcoef(X,Y)%X,Y是向量,用于求X,Y向量之间的相关系数
6.排序
[Y,I]=sort(A,dim,mode)- mode取’ascend’ or ‘descend’,默认升序
- Y是排序后的矩阵,而I记录Y中的元素在A中位置

多项式计算
1.多项式的四则运算
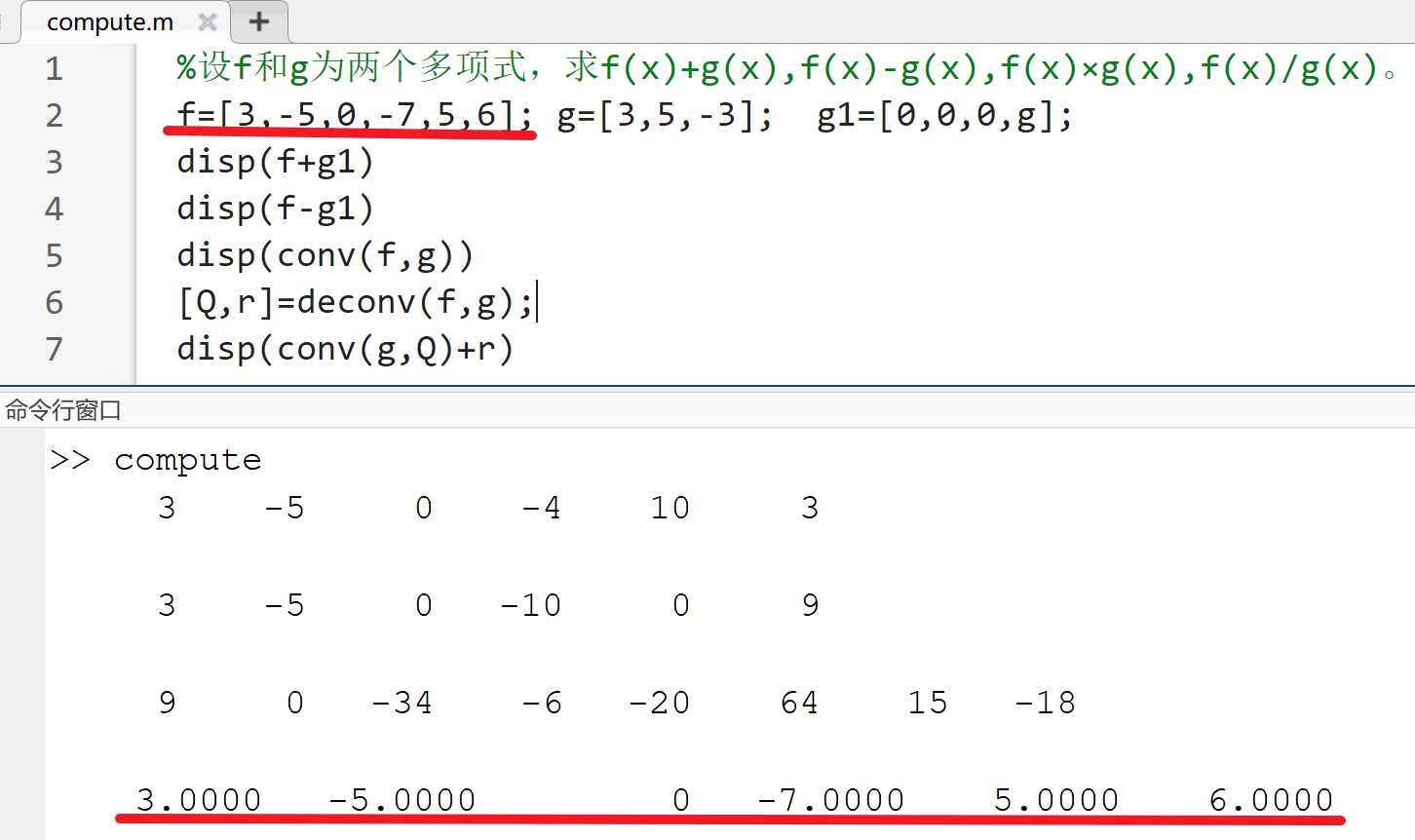
- 多项式的加减运算:直接对向量使用
+、-(两个向量长度必须一致) - 多项式乘法:
conv(P1,P2)%P1、P2是两个多项式系数向量 - 多项式相除:
[Q,r]=deconv(P1,P2)%Q返回多项式P1除以P2的商,r返回P1除以P2的余式
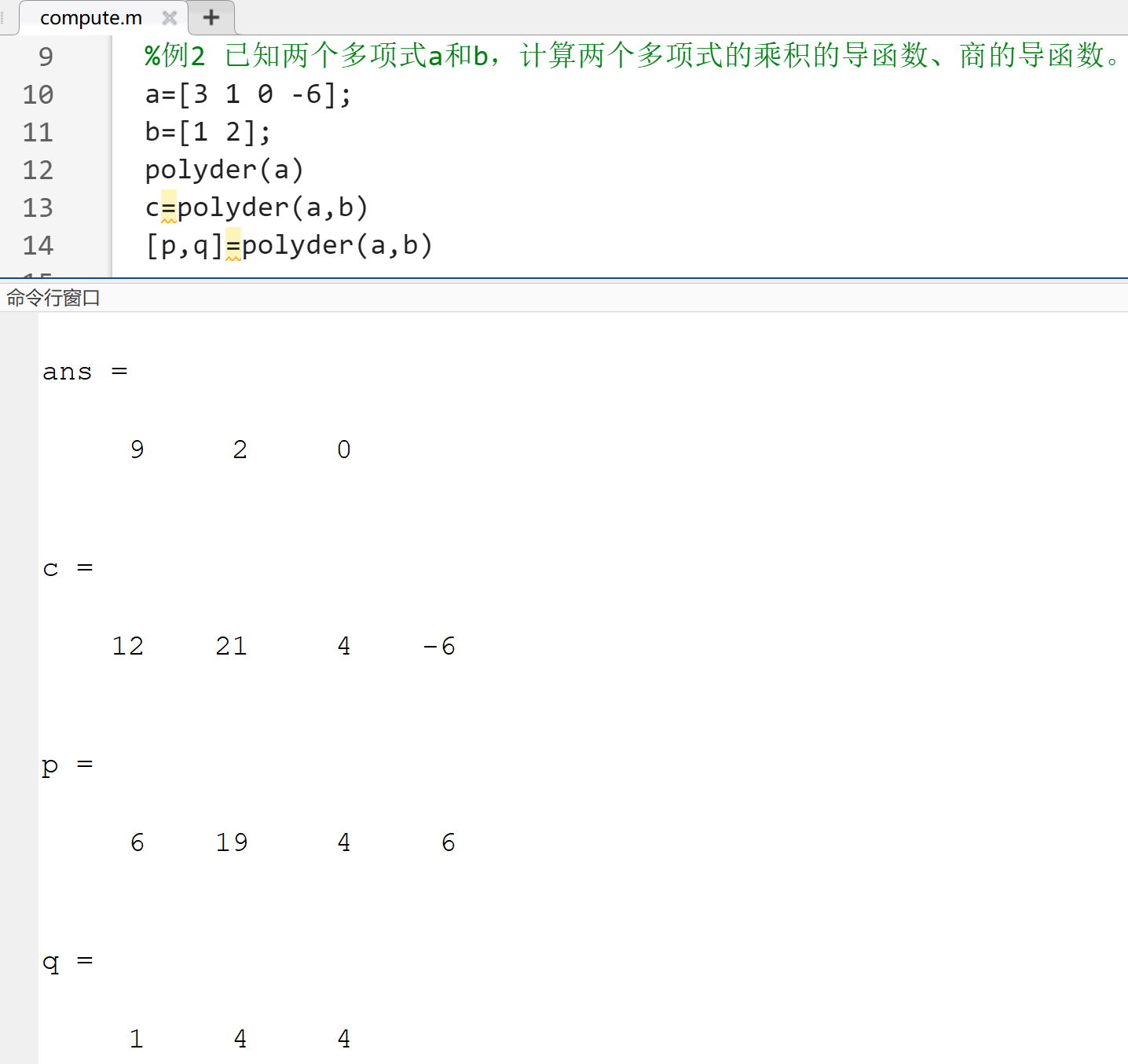
2.多项式求导
p=polyder(P)%求多项式P的导函数p=plolyder(P,Q)%求P×Q的导函数[p,q]=polyder(P,Q)%求P/Q的导函数,导函数的分子存入p,分母存入q
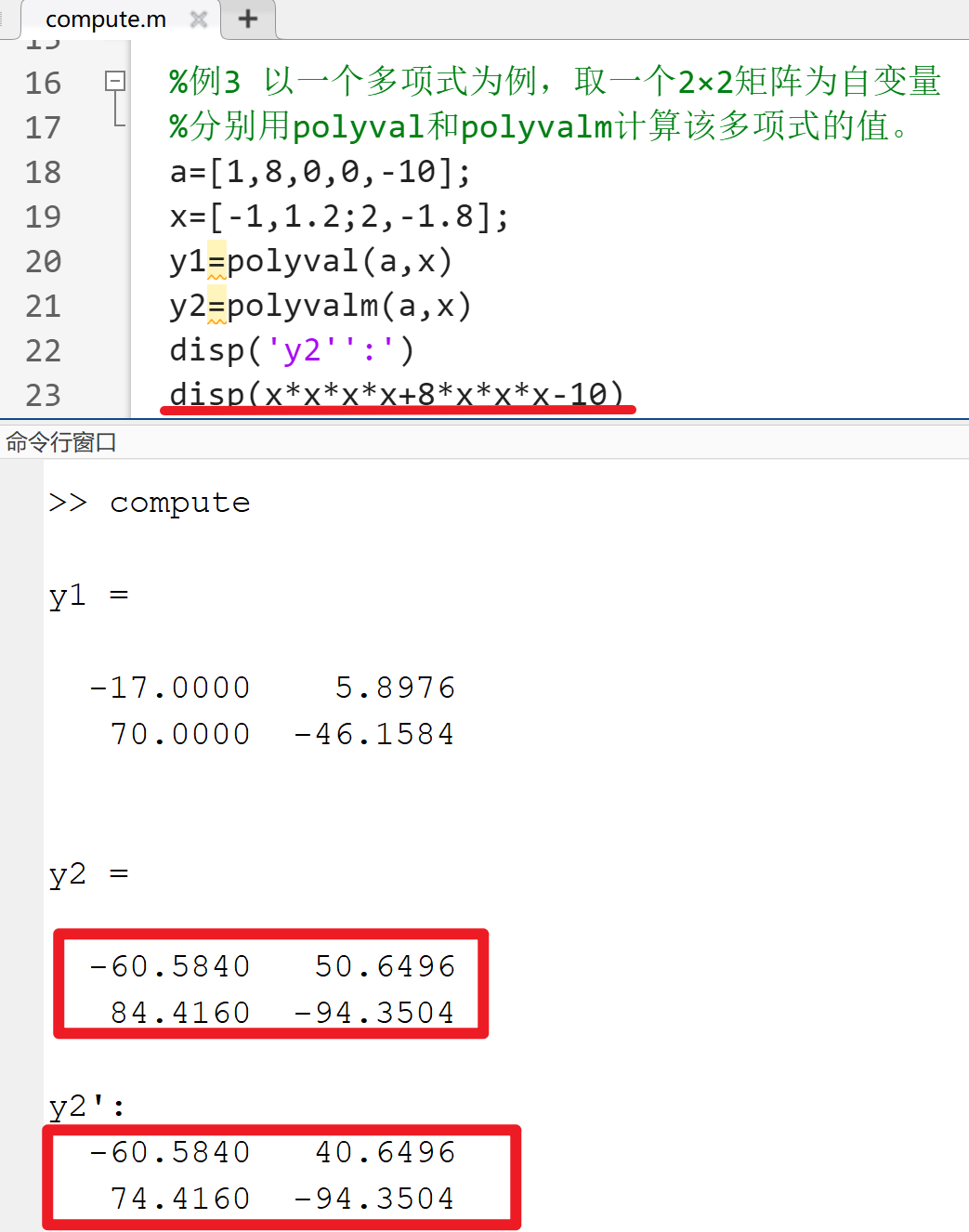
3.多项式求值
polyval(p,x)%对x中的每个数求值polyvalm(p,x)%要求x为方阵(n*n),将这个方阵作为整体带入多项式求值
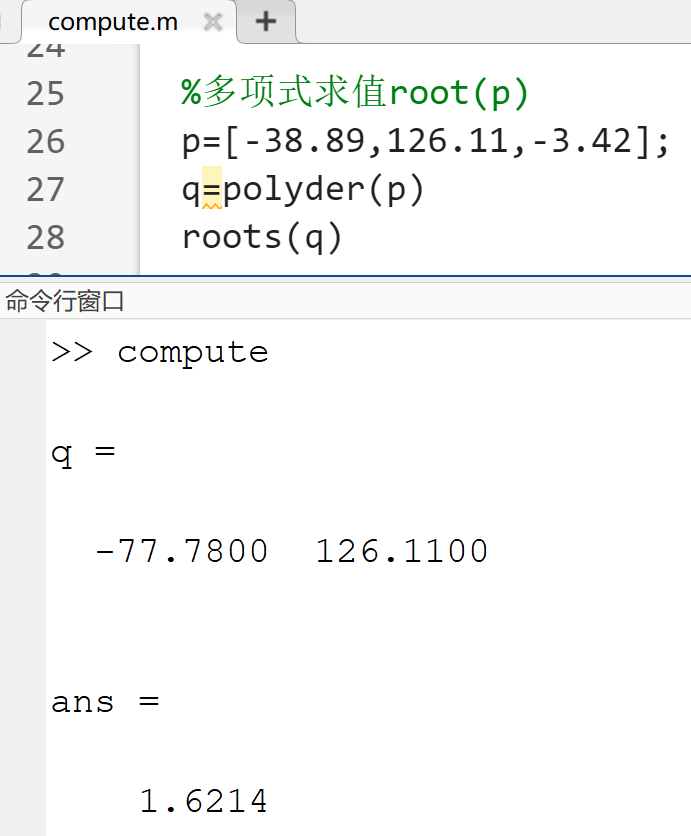
4.多项式求根
root(P)%p为多项式的系数向量
数据插值
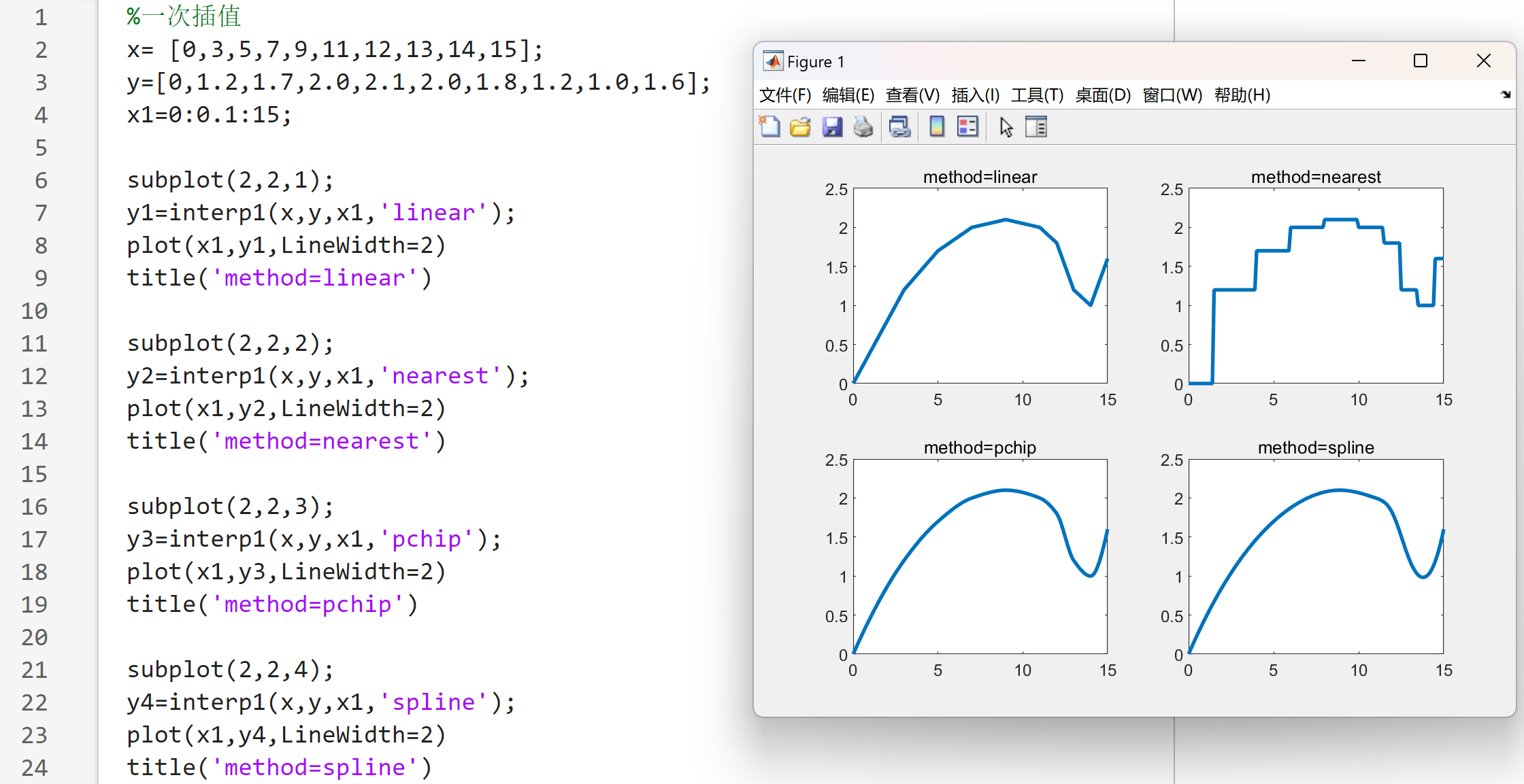
1.一维插值函数interp1(X,Y,X1,method)
- 将根据X、Y的值,计算函数在X1处的值
- 其中,X、Y是两个等长已知向量,X1是一个向量或标量,表示要插值的点
- method:插值方法
- linear:线性插值(默认方法),将与插值点靠近的两个数据点用直线连接,并在直线上选取对应插值点的数据
- nearest:最近点插值,选择最近样本点的值作为插值数据
- pchip、spline:是曲线更光滑
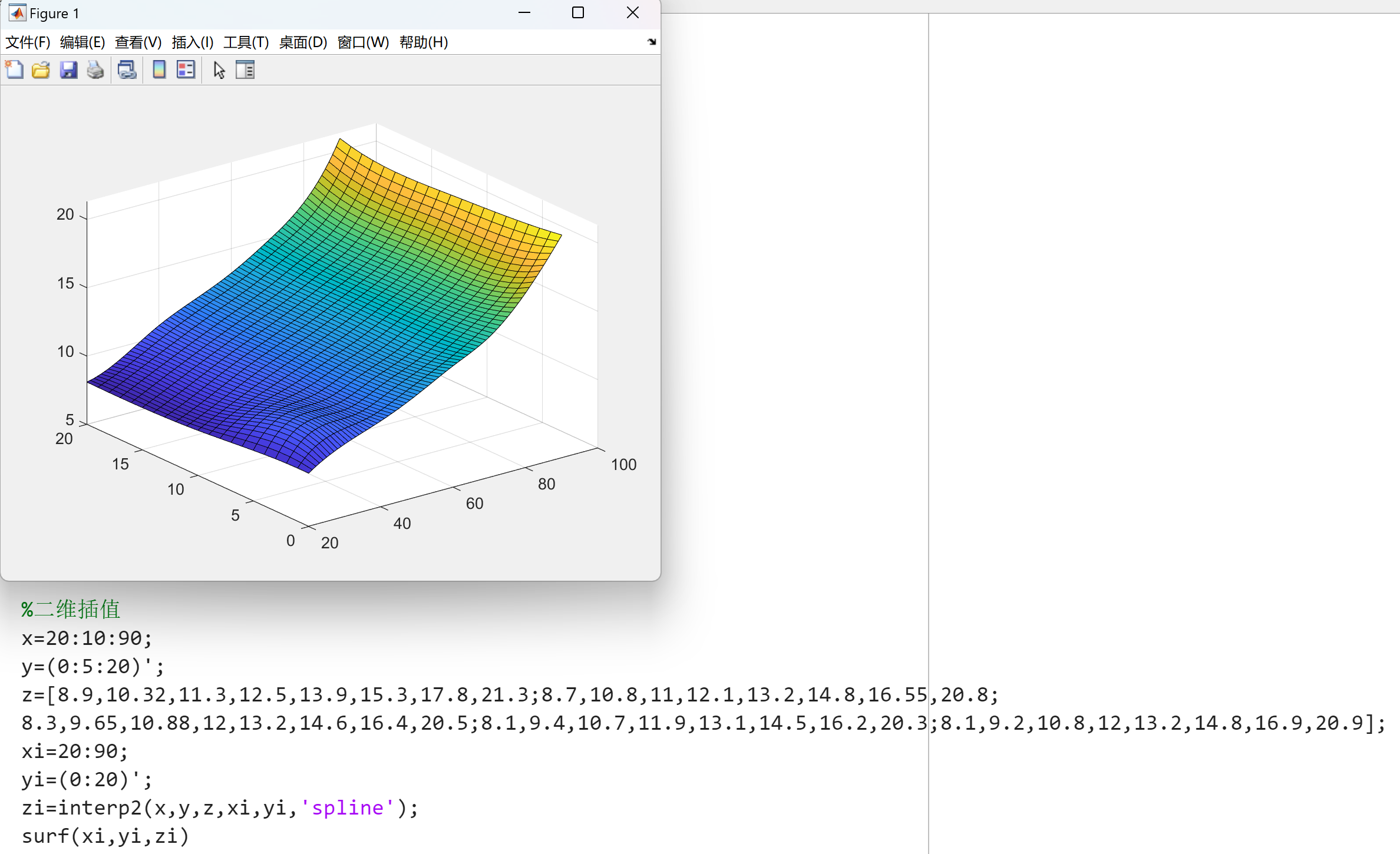
2.二维插值函数interp2(X,Y,Z,X1,Y1,method)
- 使用方法与一维相同,但不支持pchip方法
曲线拟合
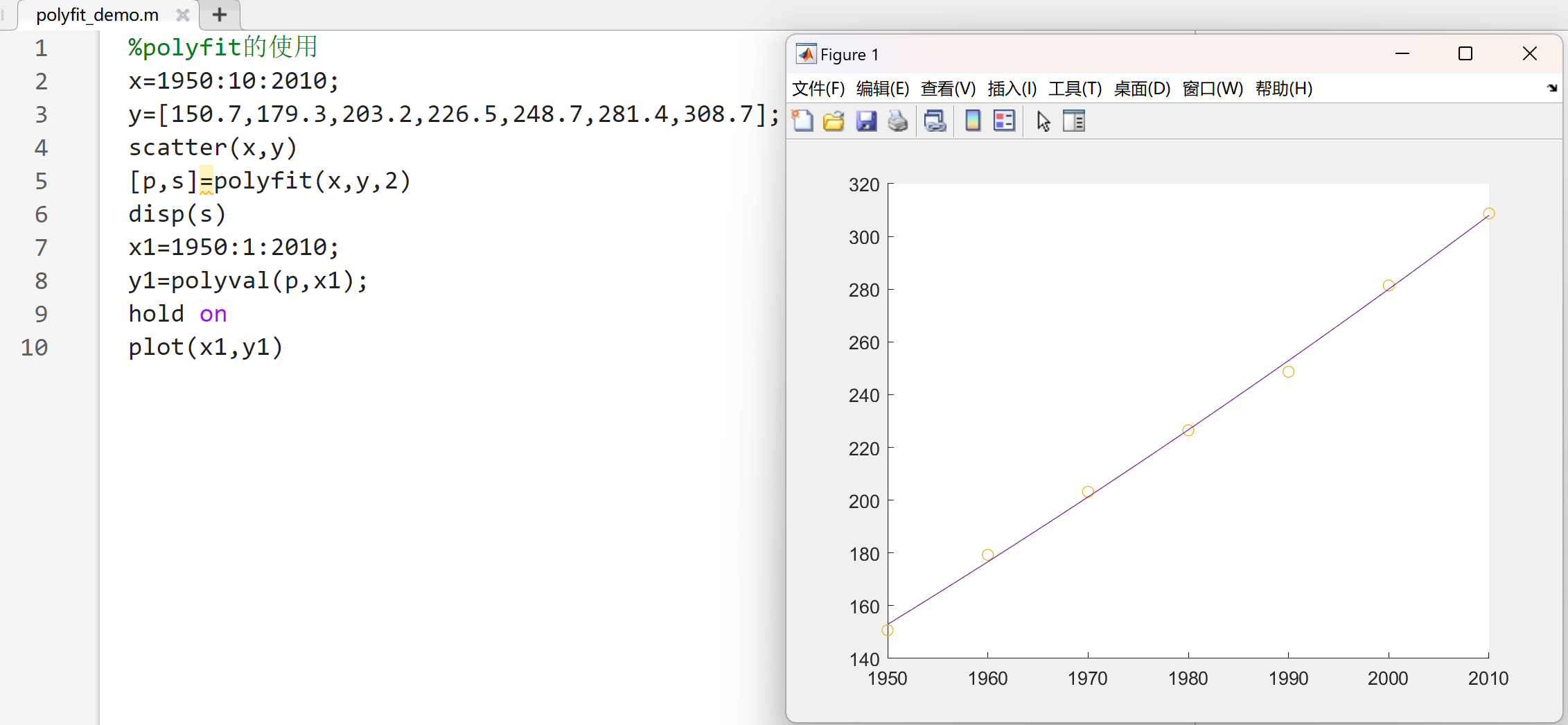
- 多项式拟合函数polyfit()
P=polyfit(X,Y,m)%X、Y是样本数据,m是拟合的阶数,P是返回的多项式的系数[P,S]=polyfit(X,Y,m)%X、Y是样本数据,m是拟合的阶数,P是返回的多项式的系数。S是结构体,包括R(系数矩阵的QR分解的上三角阵),df(自由度),normr(拟合误差平方和的算术平方根)