本节介绍了MATLAB学习的一些矩阵处理相关的知识,包括通用与专用的特殊矩阵、矩阵变换、矩阵特征值与特征向量的求解、稀疏矩阵等。
通用的特殊矩阵
- zeros函数:产生全0矩阵
- ones函数:产生全1矩阵
- eye函数:产生对角线为1的矩阵
- rand函数:产生(0,1)【不包括0和1】区间均匀分布的随机矩阵
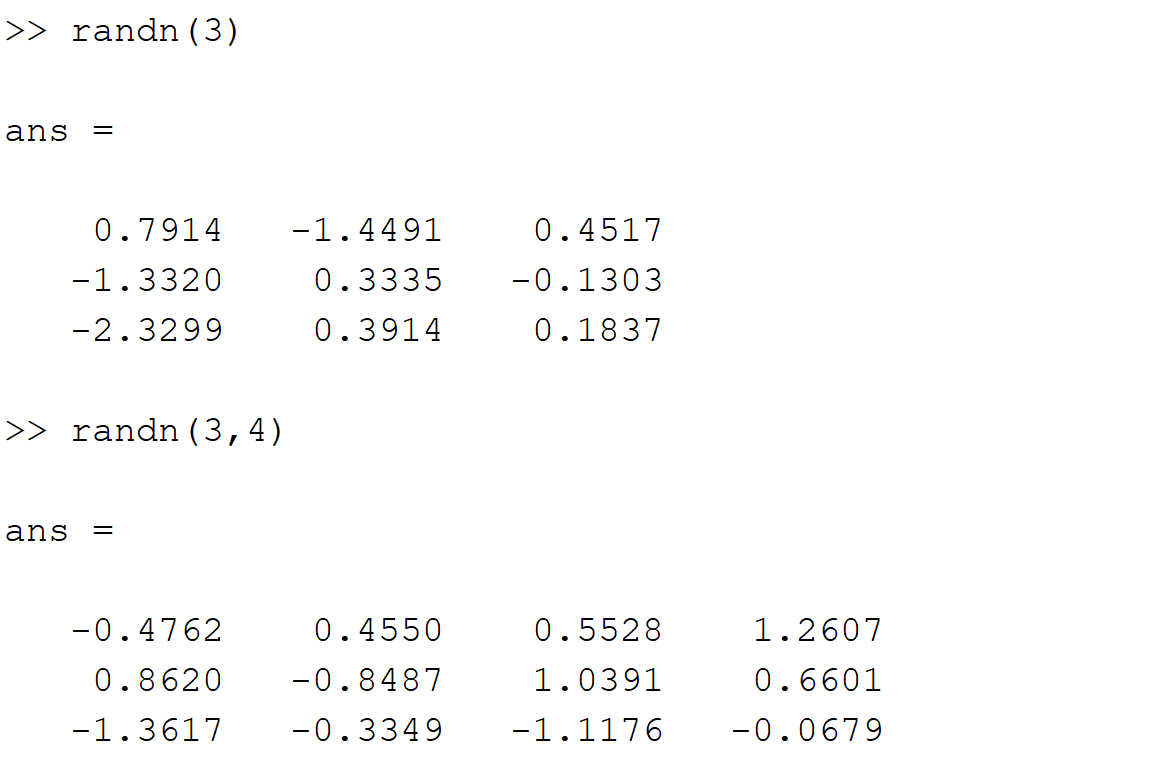
- randn函数:产生均值为0,方差为1的标准正态分布随机矩阵
- 调用方式:以zeros函数的为例:
zeros(m):产生m×m零矩阵zeros(m,n):产生m×n零矩阵zeros(size(A)):产生与矩阵A同样大小的零矩阵
用于专门学科的特殊矩阵
1.魔方矩阵(Magic Square):
magic(n)产生一个特定的魔方阵- n阶魔方阵由1,2,3,……n2共n2个整数组成,且每行、每列以及主、副对角线上各n各元素之和都相等
- n节魔方阵每行每列元素的和为(1+2+3+……+n2)/n=(n+n3)/2

2.范德蒙矩阵:vander()
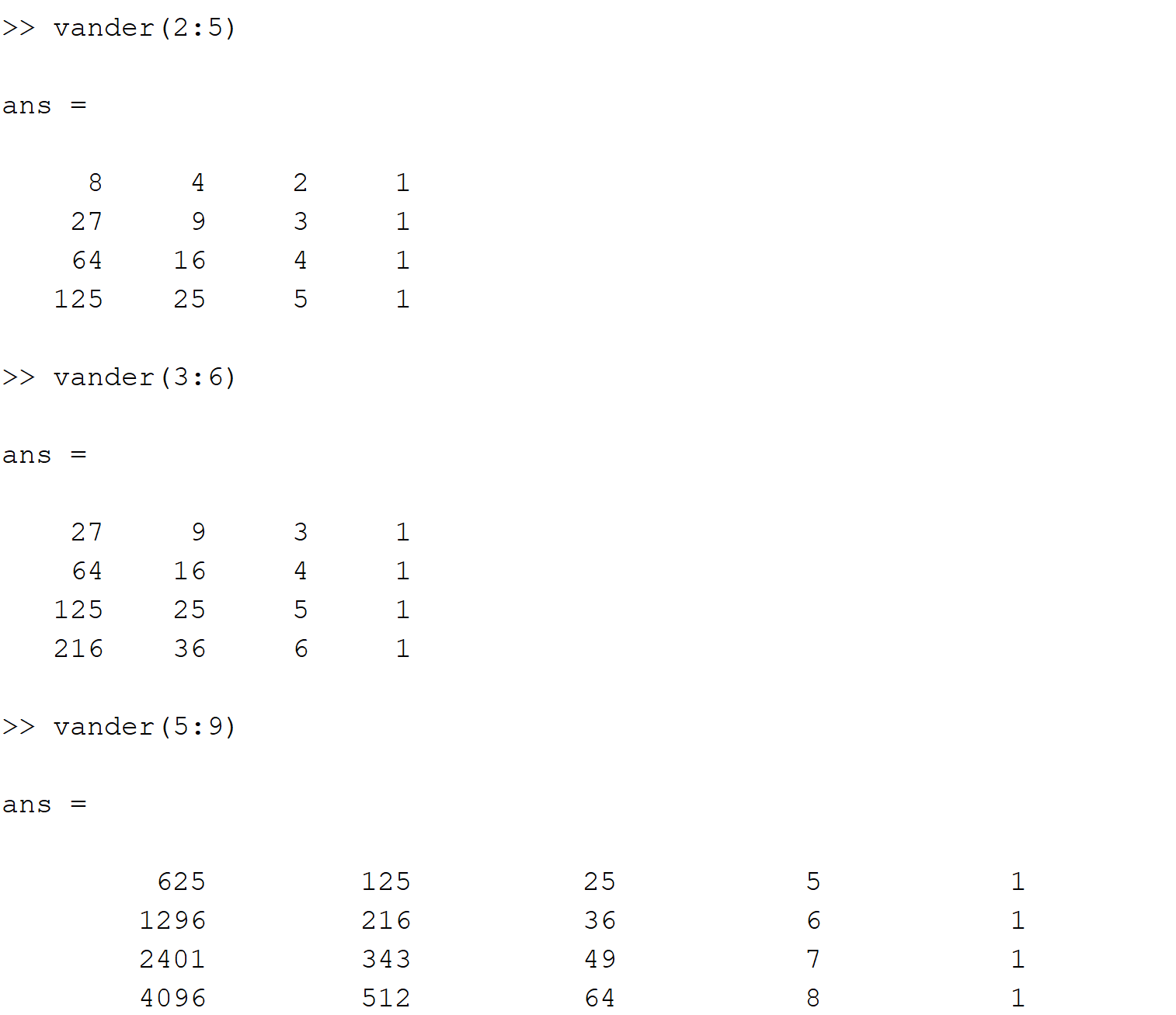
3.希尔伯特矩阵:hilb(n)

4.帕斯克矩阵:pascal(n)

矩阵变换
1.对角阵
diag(V):以向量V为主对角线元素,产生对角矩阵diag(V,k):以向量V为第k条对角线元素,产生对角矩阵diag(A,k):提取A中的第k条对角线元素,返回一个列向量

例:将A的各列元素分别乘以对角阵的对角线元素

2.三角阵:下三角矩阵(triu)和上三角矩阵(tril)
triu(A):提取矩阵A的主对角线及以上的元素triu(A,k):提取矩阵A的第k条对角线及以上的元素
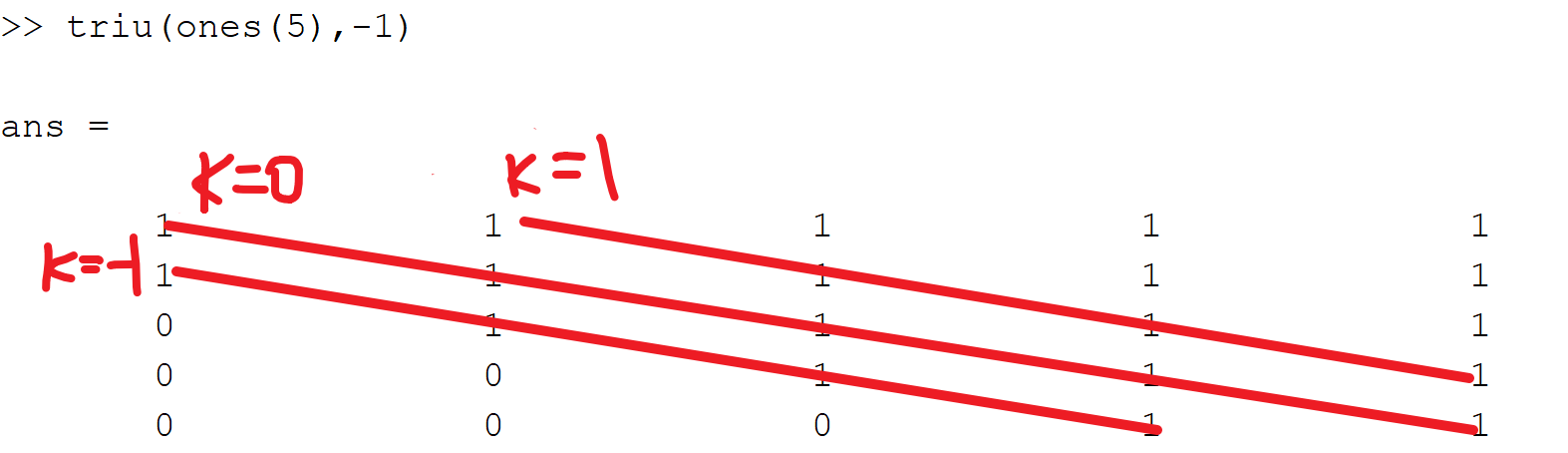
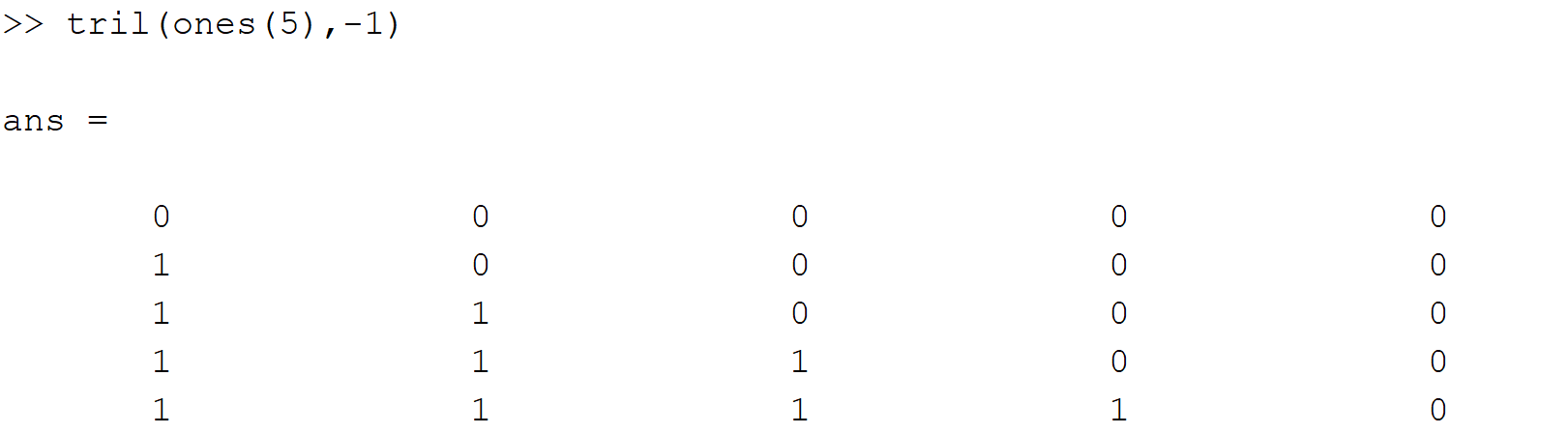
3.矩阵转置
- 转置运算符:
.' - 共轭转置:
'%它在转置的基础上还要取每个数的复共轭

4.矩阵的旋转
rot90(A,k)- 将矩阵A逆时针方向旋转90°的k倍,当k为1时可省略

5.矩阵的翻转
fliplr(A):左右翻转flipud(A):上下翻转

6.矩阵的求逆
inv(A)可以通过矩阵求逆的方法求解线性方程组
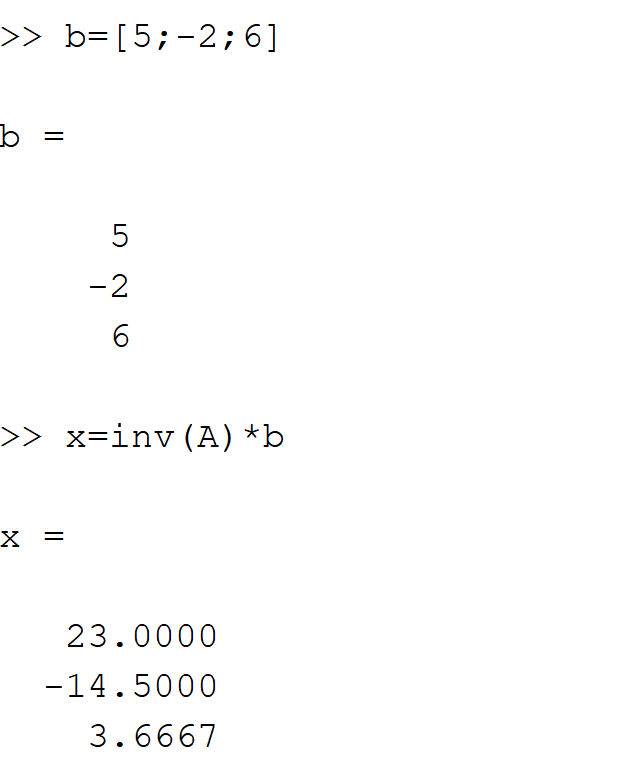
矩阵行列式求解
det(A)

矩阵的特征值与特征向量
- 设A时n阶方阵,如果存在常数$\lambda$和n维非零列向量x,使得等式Ax=$\lambda$x成立,则称$\lambda$为A的特征值,x是对应特征值$\lambda$的特征向量
E=eig(A):求矩阵A的全部特征值,构成向量E[X,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并产生矩阵X,X各列是相应的特性向量

稀疏矩阵
1.无规则结构稀疏矩阵的产生
A=sparse(S):将矩阵S转化为稀疏存储方式的矩阵AS=full(A):将矩阵A转化为完全存储方式的矩阵S

sparse(m,n):生成一个m×n的所有元素都是零的稀疏矩阵sparse(i,j,S):i,j是存储元素的下标,S表示要存储的非零元素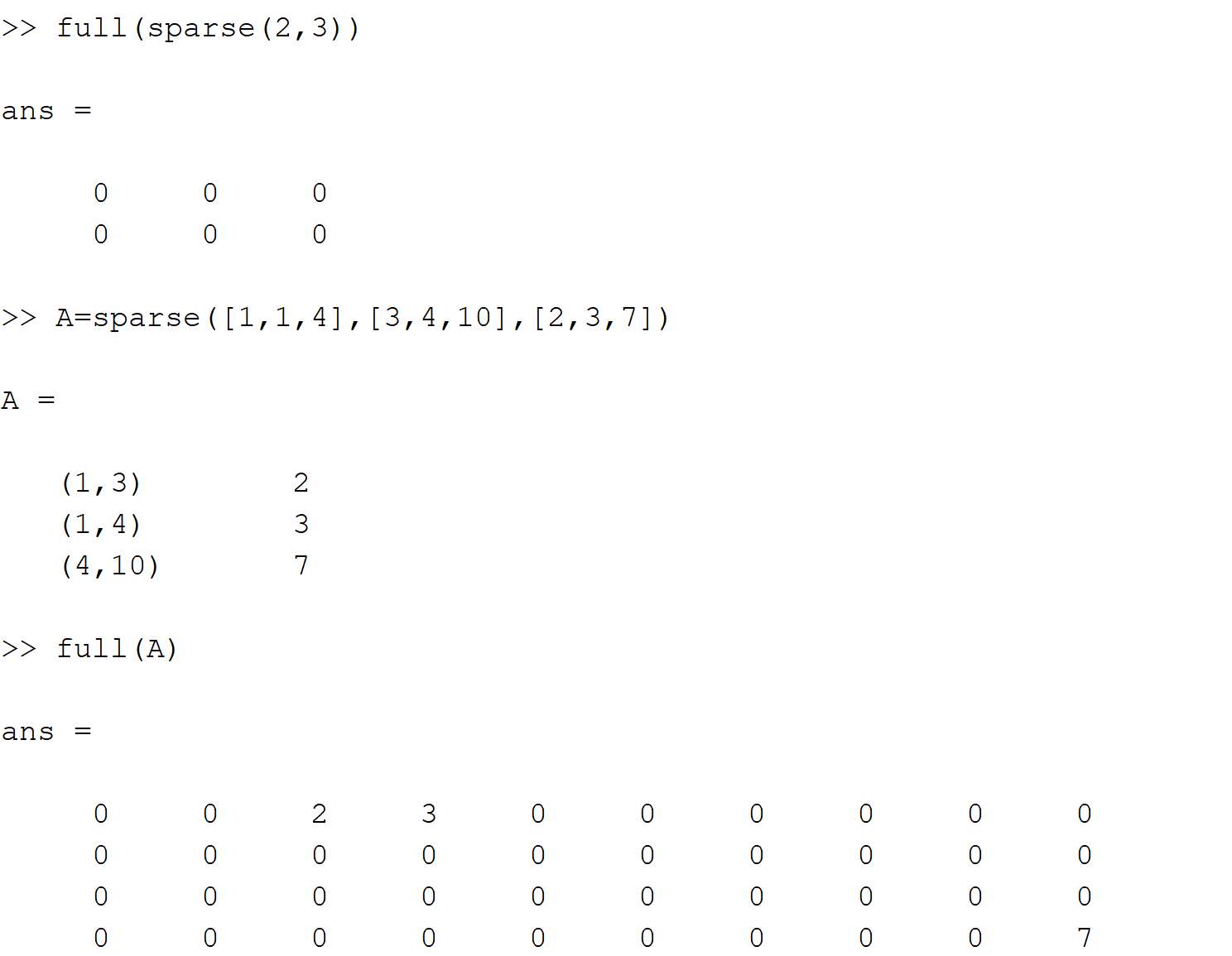
2.带状稀疏矩阵的产生
其是指所有非零元素集中在对角线上的矩阵
[B,d]=spdiags(A):从带状稀疏矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线的位置向量d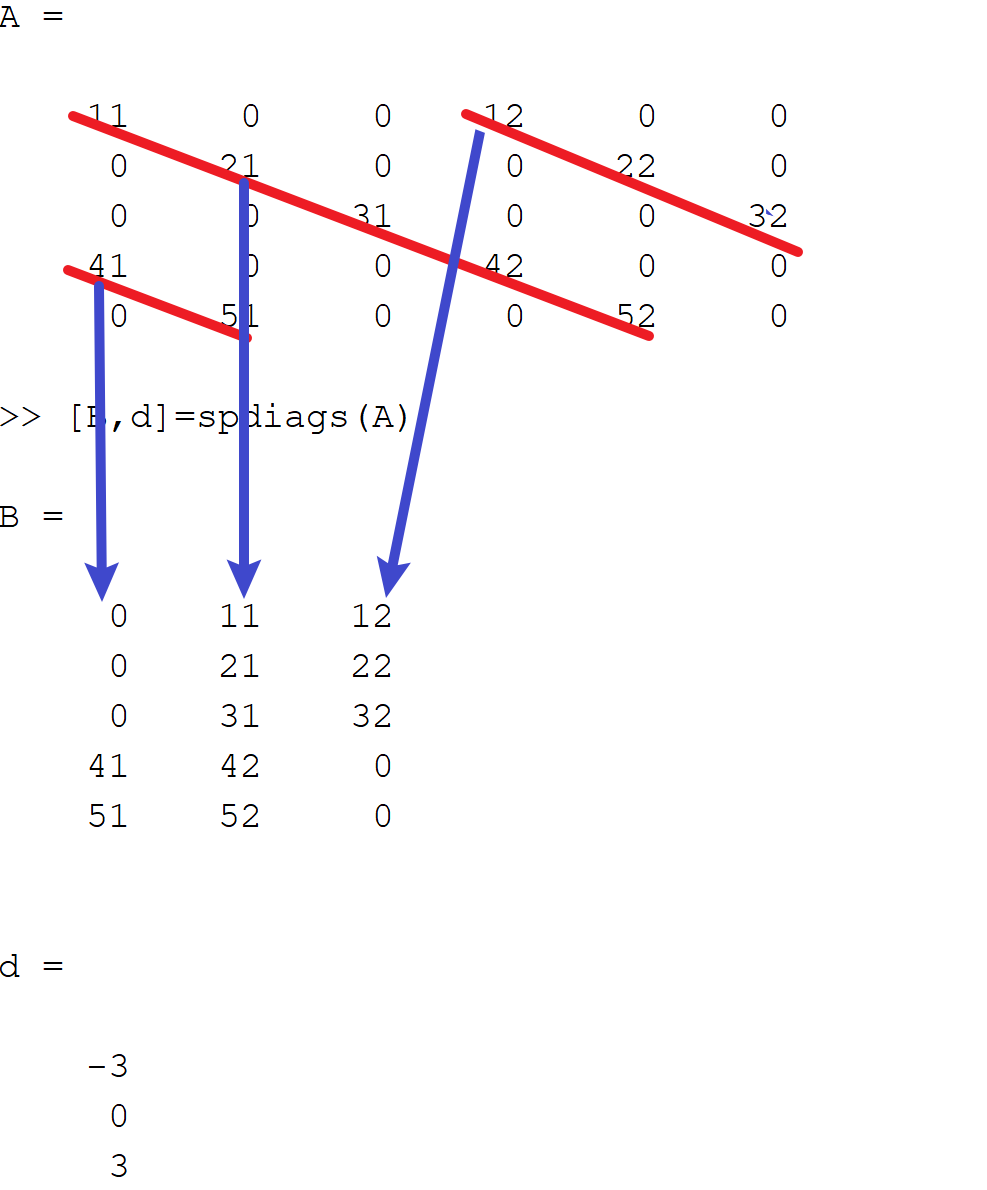
A=spdiags(B,d,m,n)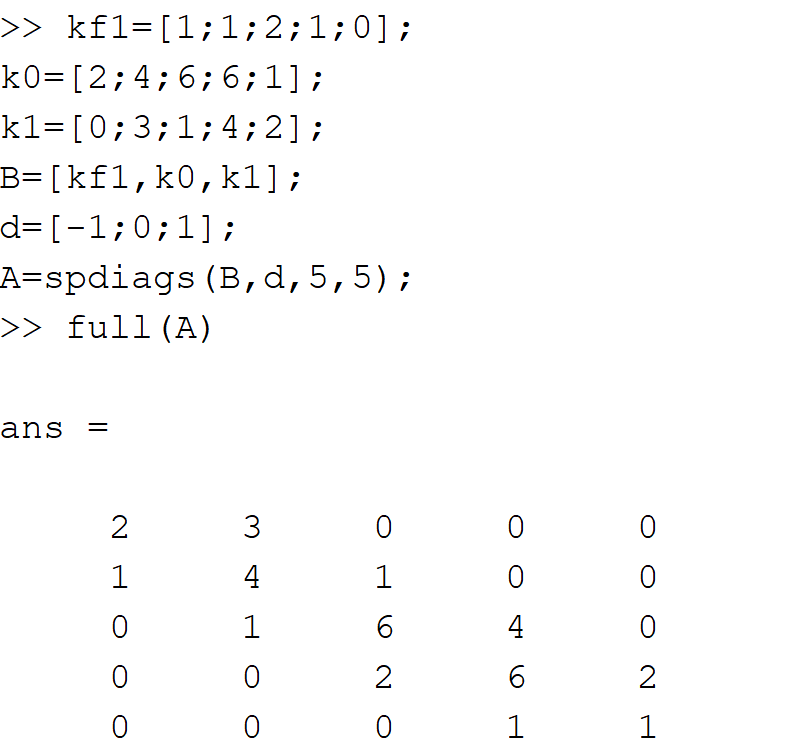
speye(m,n):返回m×n的稀疏存储的单位矩阵
