本节从单层神经网络到多层神经网络,一步步介绍了神经网络的基本结构与简单实现,并借助TensorFlow框架中提供的Sequential模型,快速进行神经网络的搭建与训练。
单层神经网络的实现
1.单层神经网络的设计
- 神经网络的结构:单层前馈型神经网络
- 激活函数:softmax函数
- 损失函数:交叉熵损失函数
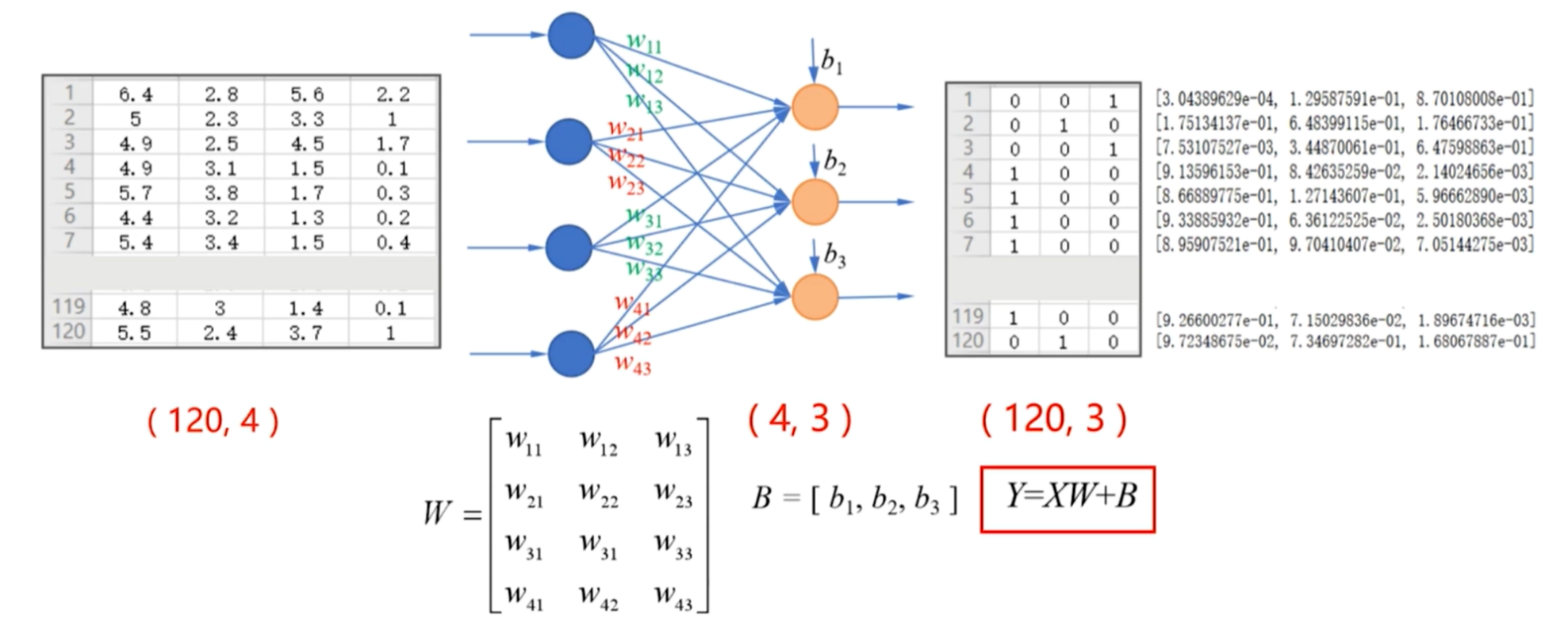
2.单层神经网络实现的相关函数
softmax函数:
tf.nn.softmax()- tf.nn.softmax(tf.matmul(X_train,W)+B)
独热编码:
tf.one_hot(indices,depth)- tf.one_hot(tf.constant(y_test,dtype=tf.int32),3)
交叉熵损失函数:
tf.keras.losses.categorical_crossentropy(y_true,y_pred)- y_true表示为独热编码的标签值
- y_pred为softmax函数的输出
- 其返回的是每个样本的交叉熵损失
- 则平均交叉熵损失为:tf.reduce_mean(tf.keras.losses.categorical_crossentropy(y_true=Y_train,y_pred=PRED_train))
3.单层神经网络的代码实现
1 | #1.导入库,加载数据 |
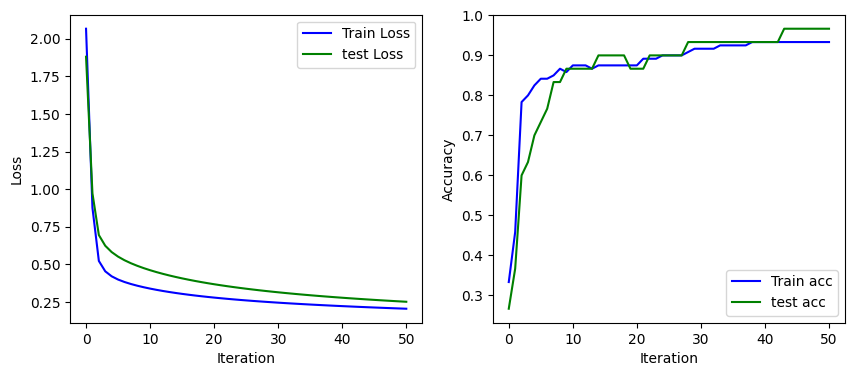
结果如下:
i:0 Train Acc:0.333333 Train Loss:2.066978, Test Acc:0.266667 Test Loss:1.880856
i:10 Train Acc:0.875000 Train Loss:0.339410, Test Acc:0.866667 Test Loss:0.461705
i:20 Train Acc:0.875000 Train Loss:0.279647, Test Acc:0.866667 Test Loss:0.368414
i:30 Train Acc:0.916667 Train Loss:0.245924, Test Acc:0.933333 Test Loss:0.314814
i:40 Train Acc:0.933333 Train Loss:0.222922, Test Acc:0.933333 Test Loss:0.278643
i:50 Train Acc:0.933333 Train Loss:0.205636, Test Acc:0.966667 Test Loss:0.251937
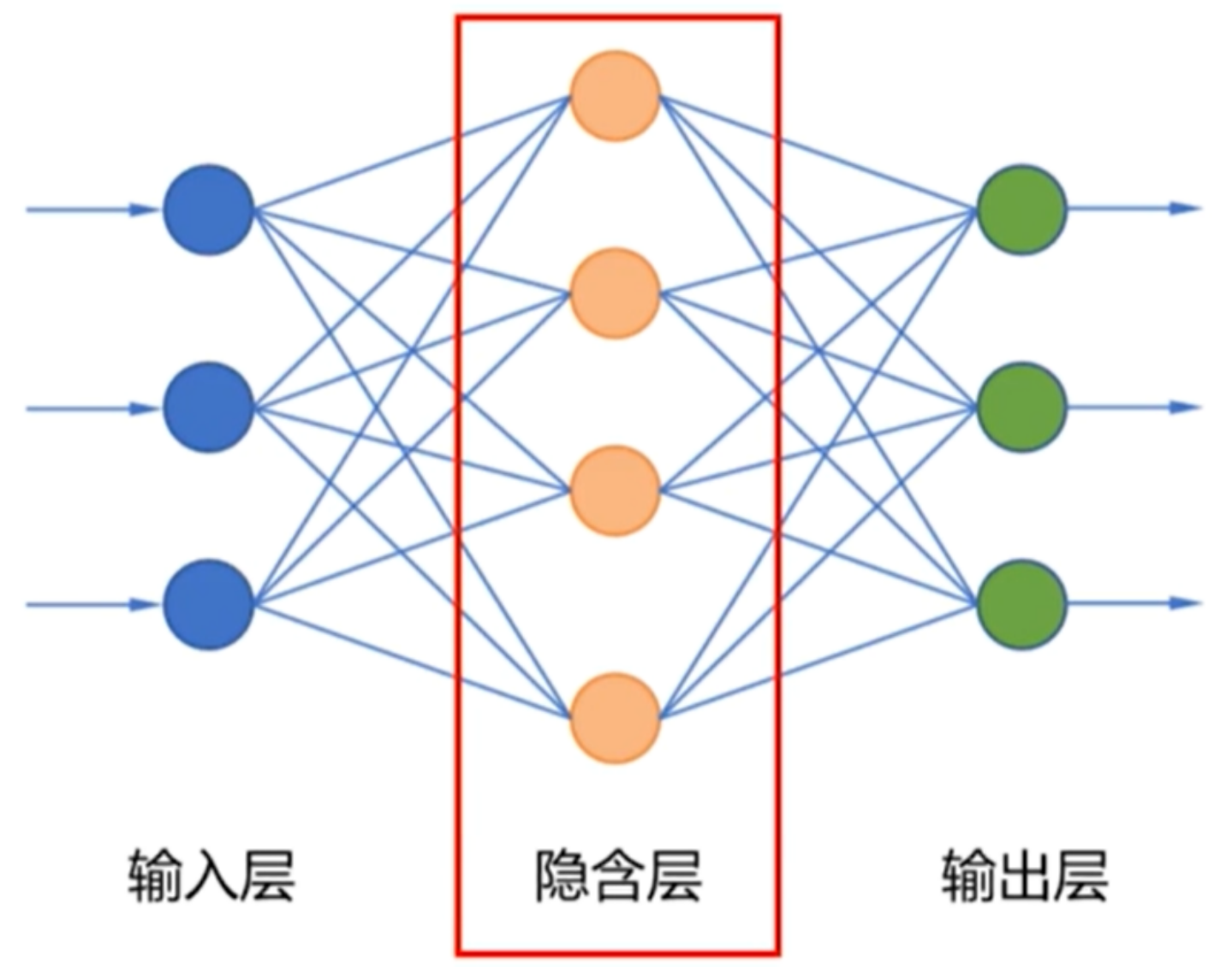
多层神经网络
- 具有隐含层的神经网络称为多层神经网络
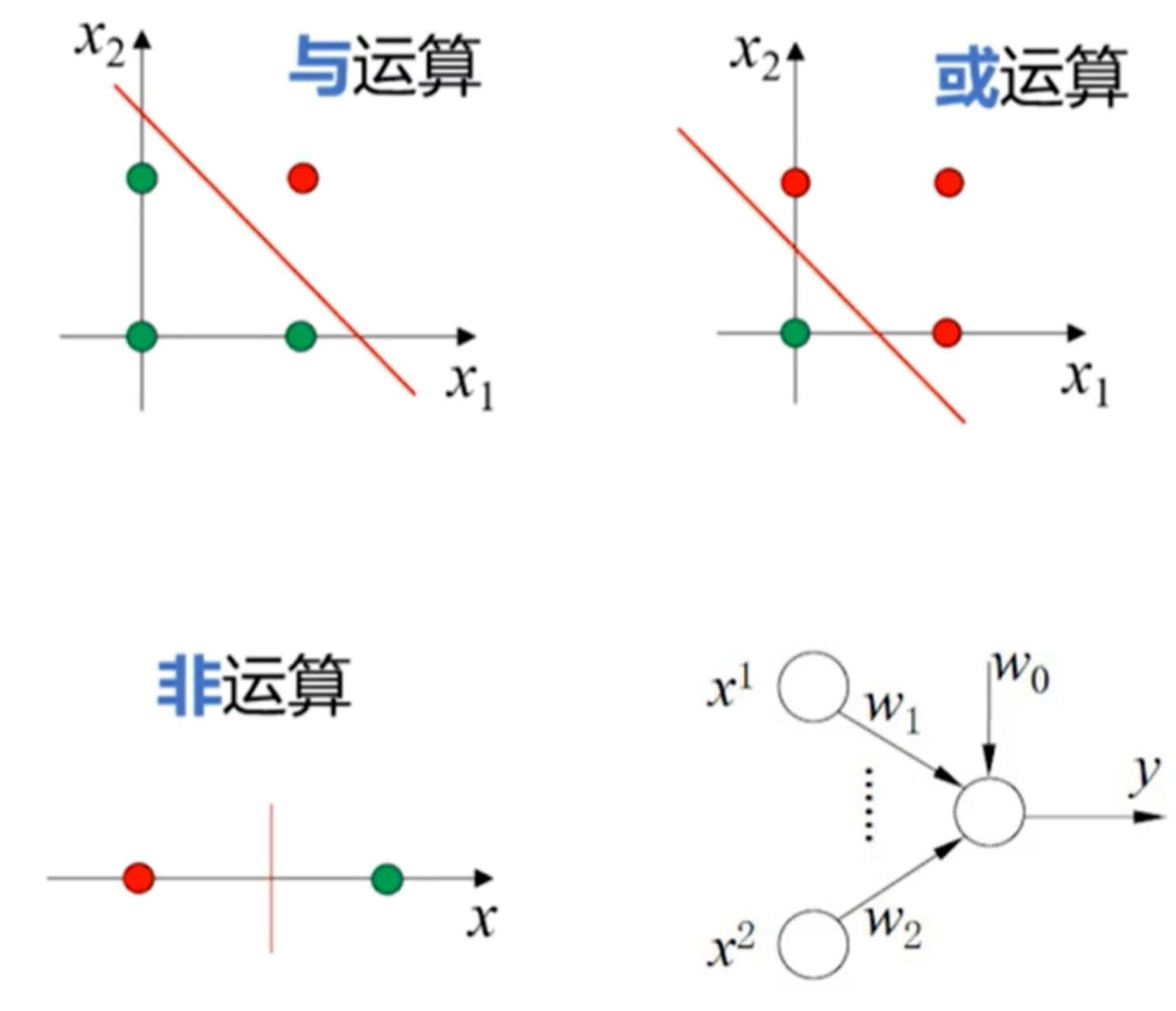
1.线性分类器
- 与运算
- 或运算
- 非运算
- 对感知机(二分类的线性分类模型)给定一个合适的权值向量即可实现运算
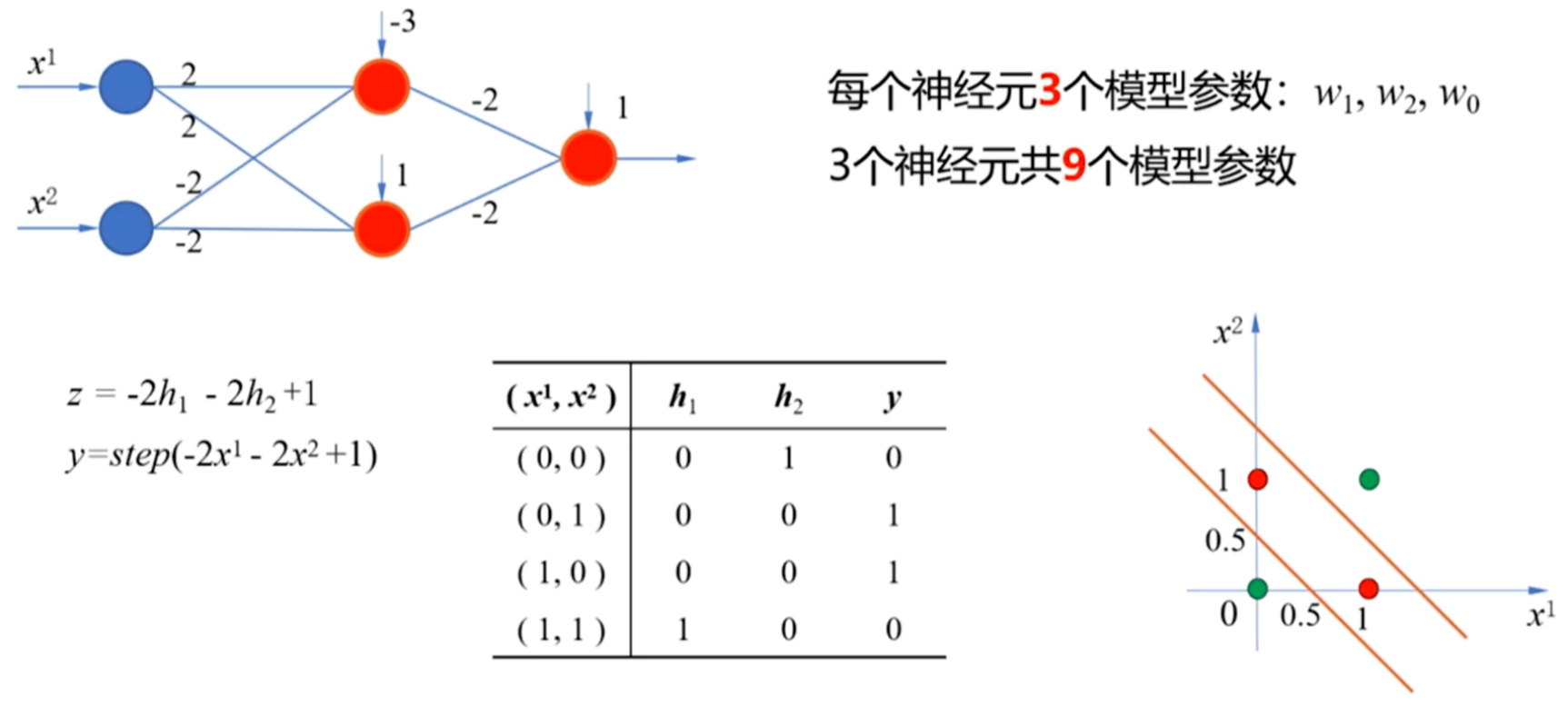
2.通过实现异或运算进而理解多层神经网络
- 隐藏层由与运算与或非运算两个感知机组成
- 这两个感知机的输出作为下一层神经元的输入
- 增加的这一层权值(W)和阈值(B)与前一层的第二个感知机一样,则也是实现了或非运算
- 红圈为有计算能力的神经元
- 一个感知机对应一根直线
3.线性不可分数据集的分类思路
- 弯曲的直线可以看成是多条直线的线性组合
- 其中的每一条直线可以用一个感知机来实现
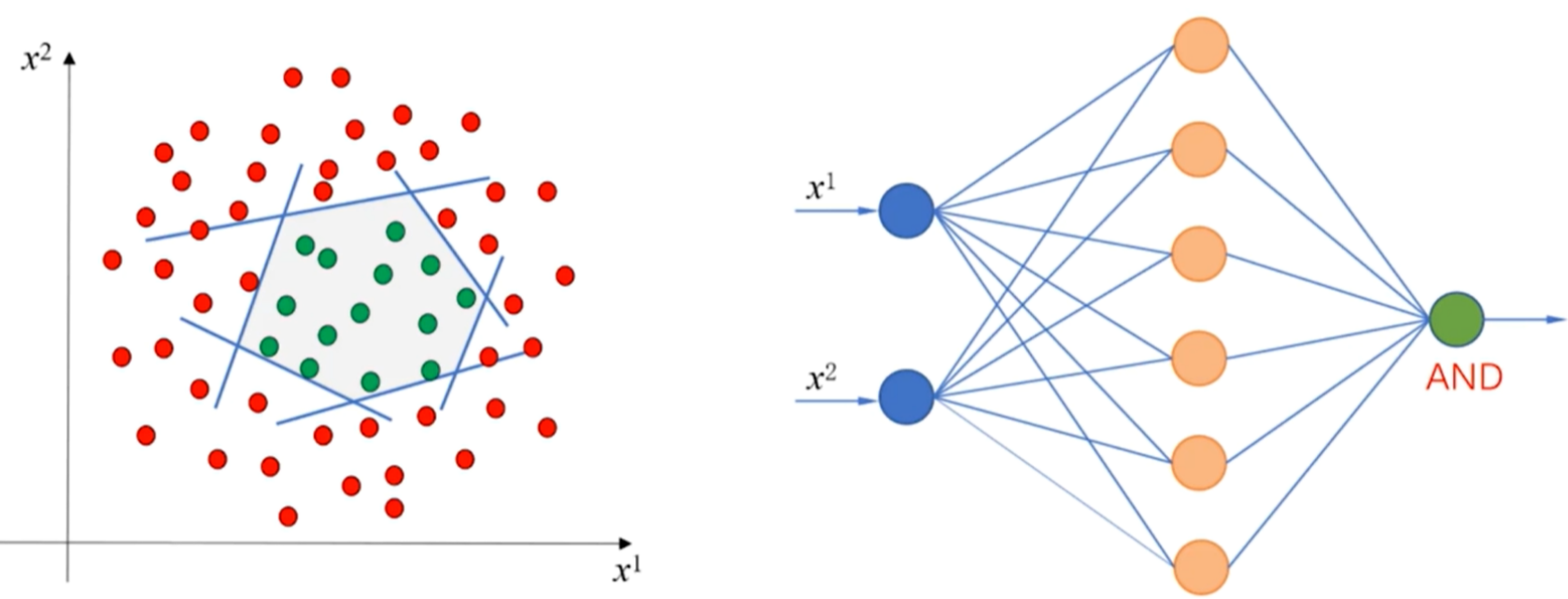
- 如果神经网络中有足够的隐藏层,每个隐藏层中有足够多的神经元,神经网络就可以表示任意复杂的函数或空间分布
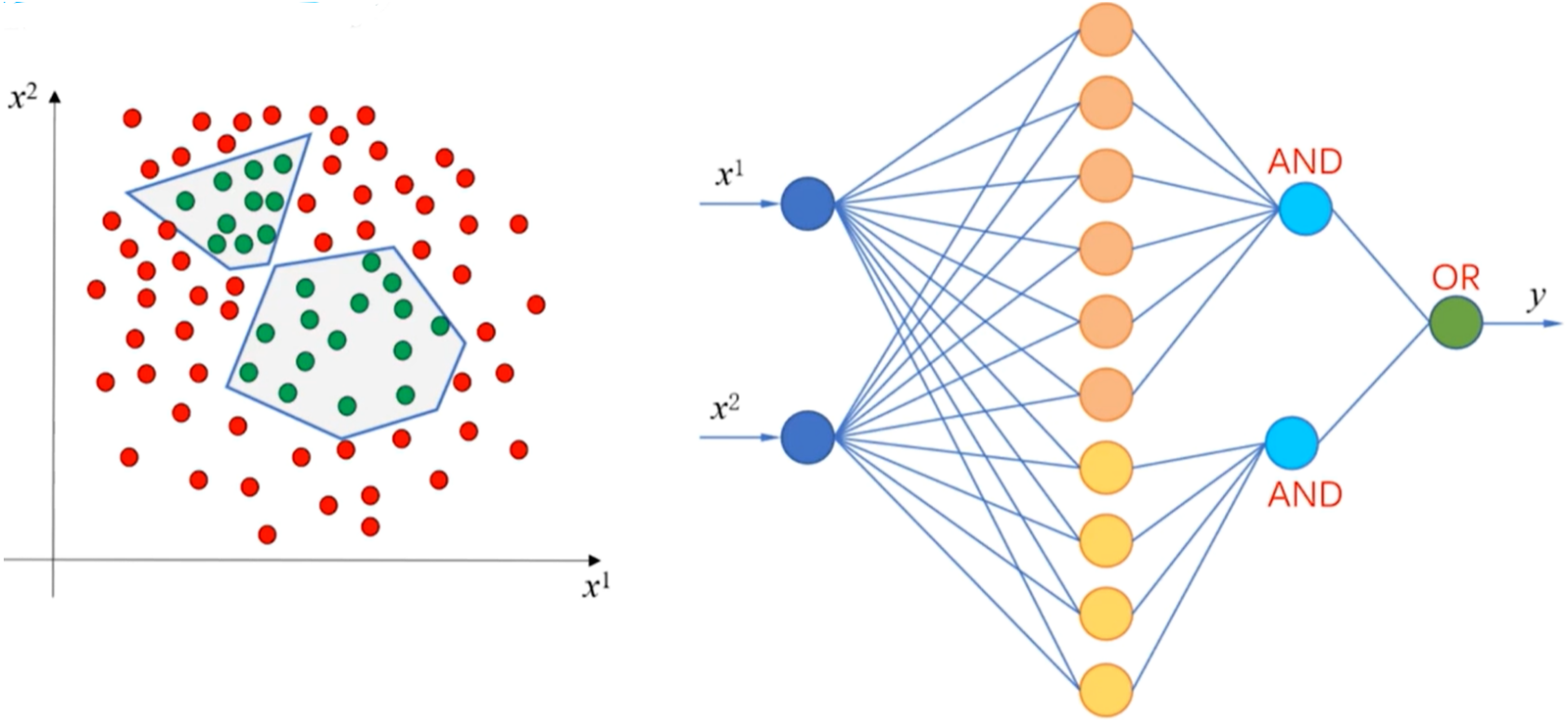
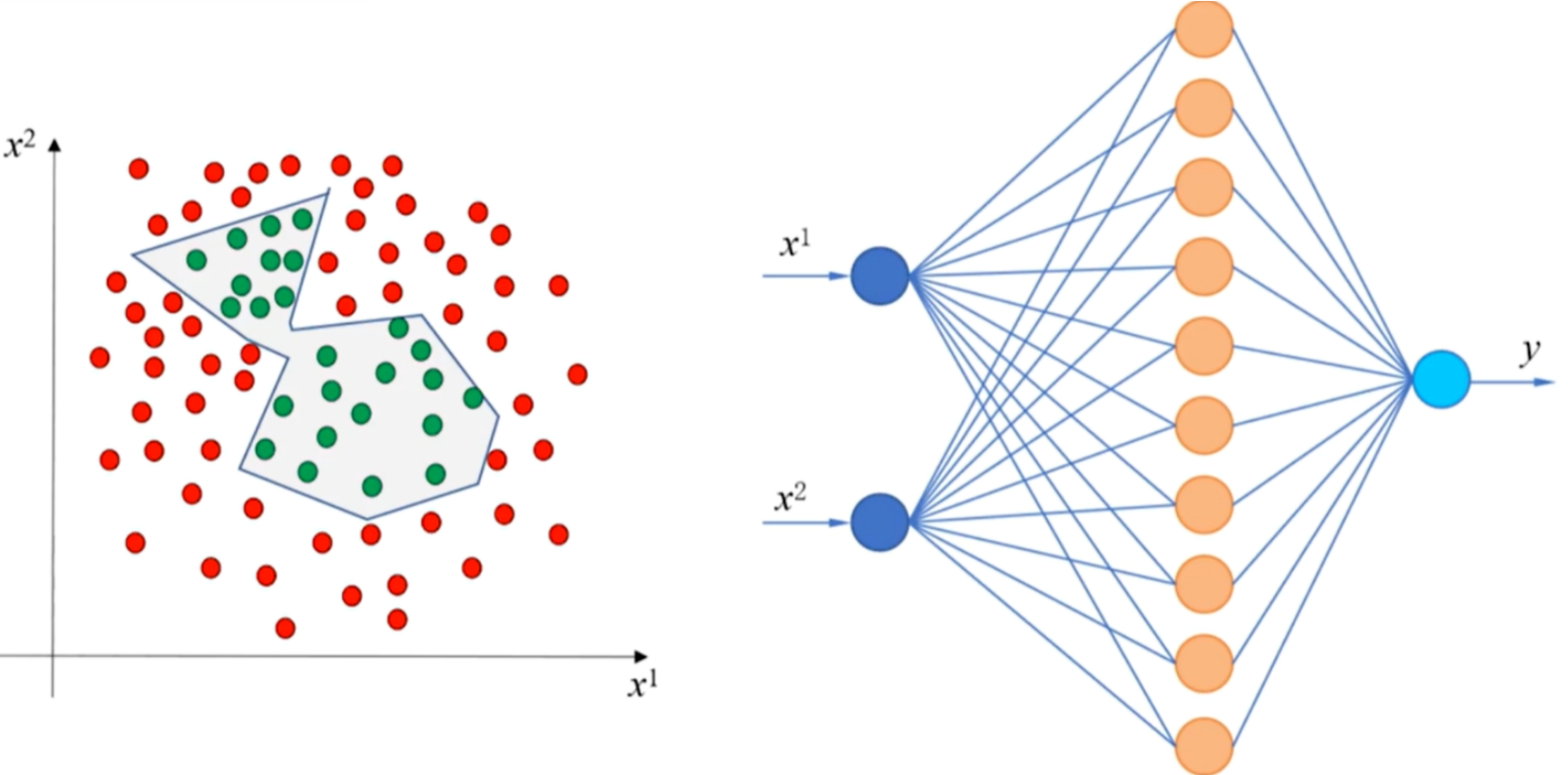
- 多隐含层神经网络:能够表示非连续的函数或空间区域,减小泛化误差,减小每层神经元的数量
4.前馈神经网络(Feedforward Neural Network)
- 每层神经元只与前一层的神经元相连
- 处于同一层的神经元之间没有连接
- 各层间没有反馈,不存在跨层连接
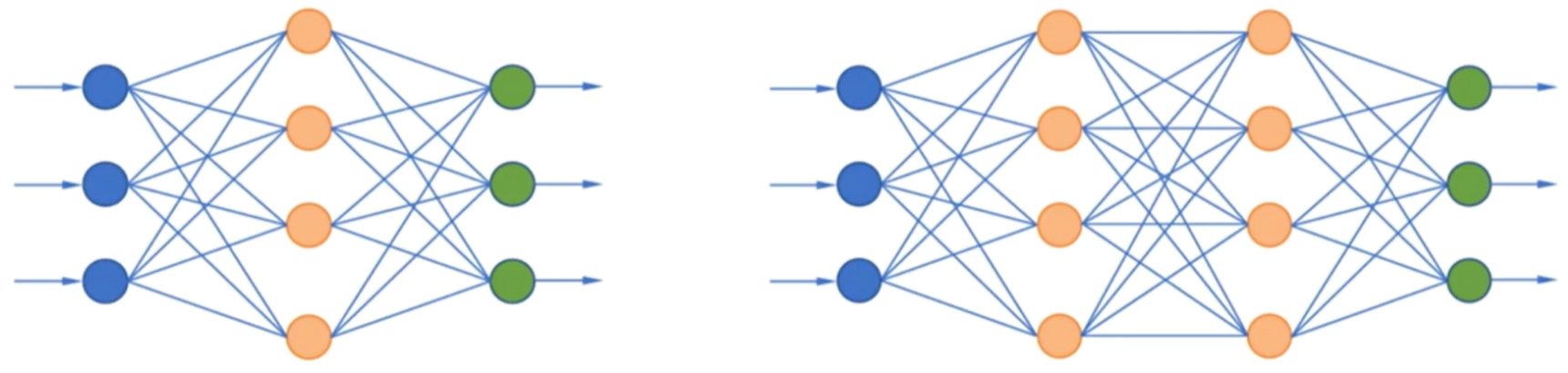
- 万能近似定理:在前馈型神经网络中,只要有一个隐含层,并且这个隐含层中有足够多的神经元,就可以逼近任意一个连续的函数或空间分布
5.全连接网络(Full Connected Network)
- 每一层中的任何一个节点都与其后面一层的所有节点连接
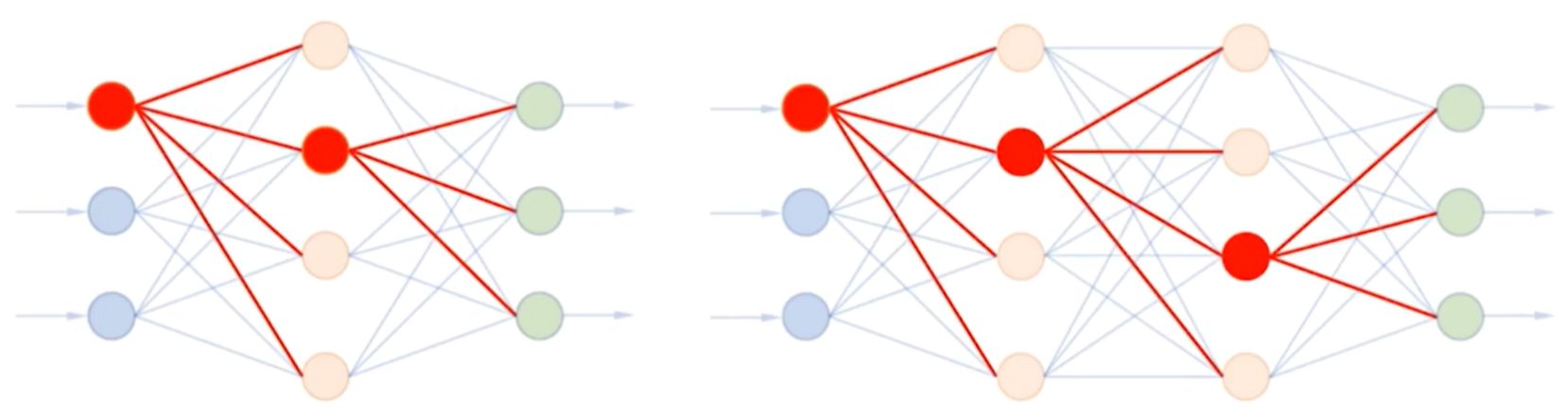
- 第n层中的每个节点接收来自第n-1层中所有节点的输入
6.超参数与验证集
- 训练集:训练模型,确定模型参数
- 验证集:确定超参数
- 测试集:评估模型的泛化能力
误差反向传播算法
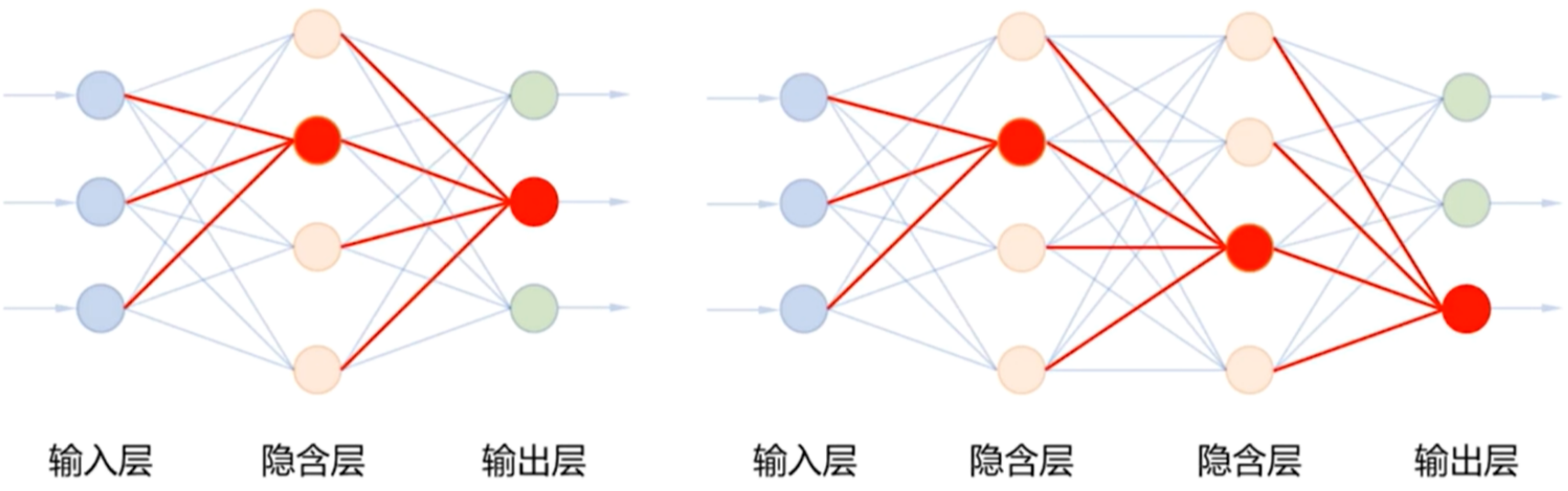
- 通过误差反向传播法计算梯度
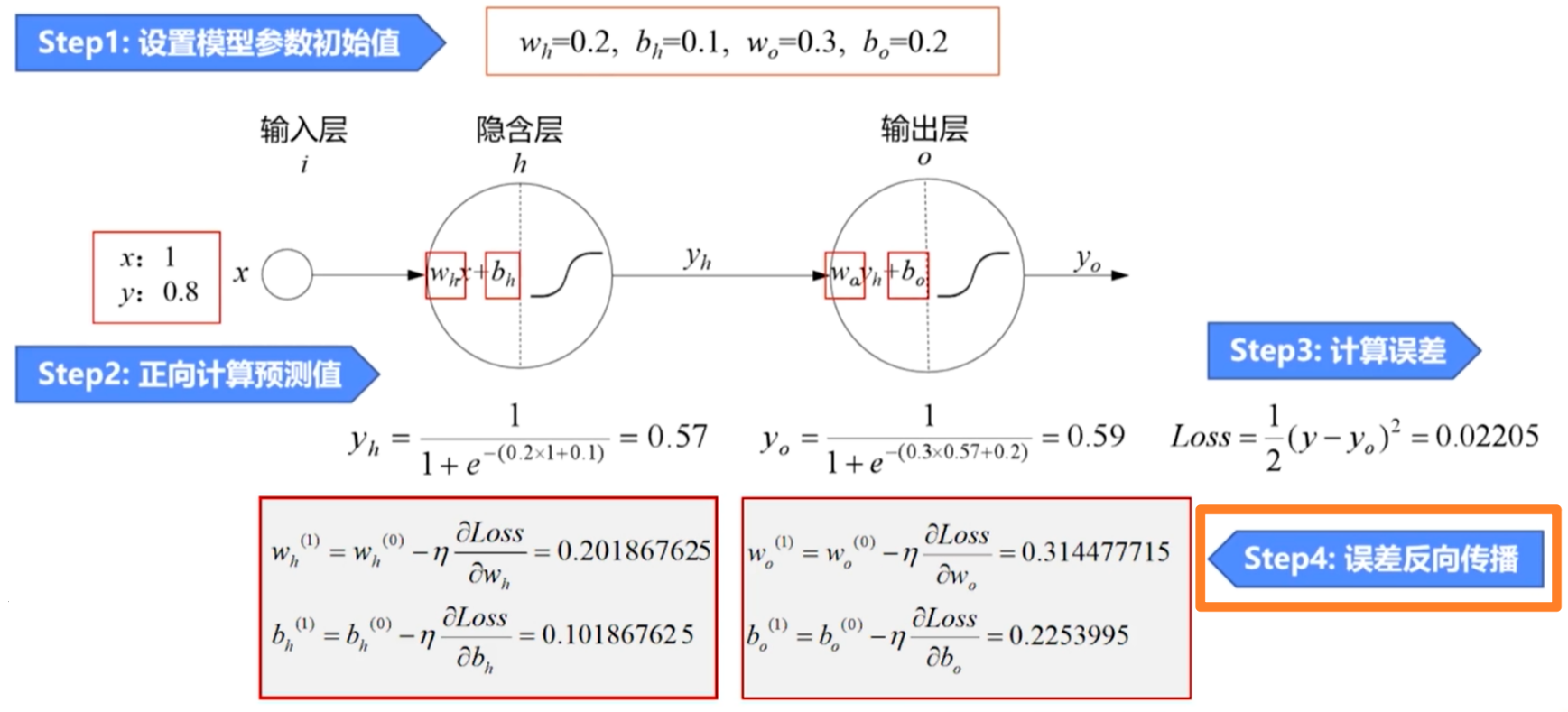
- 先计算输出层对误差的梯度,进而更新输出层的权值

- 再计算隐藏层对误差的梯度,进而更新隐藏层的权值

- 输出端有多个神经元的误差反向传播
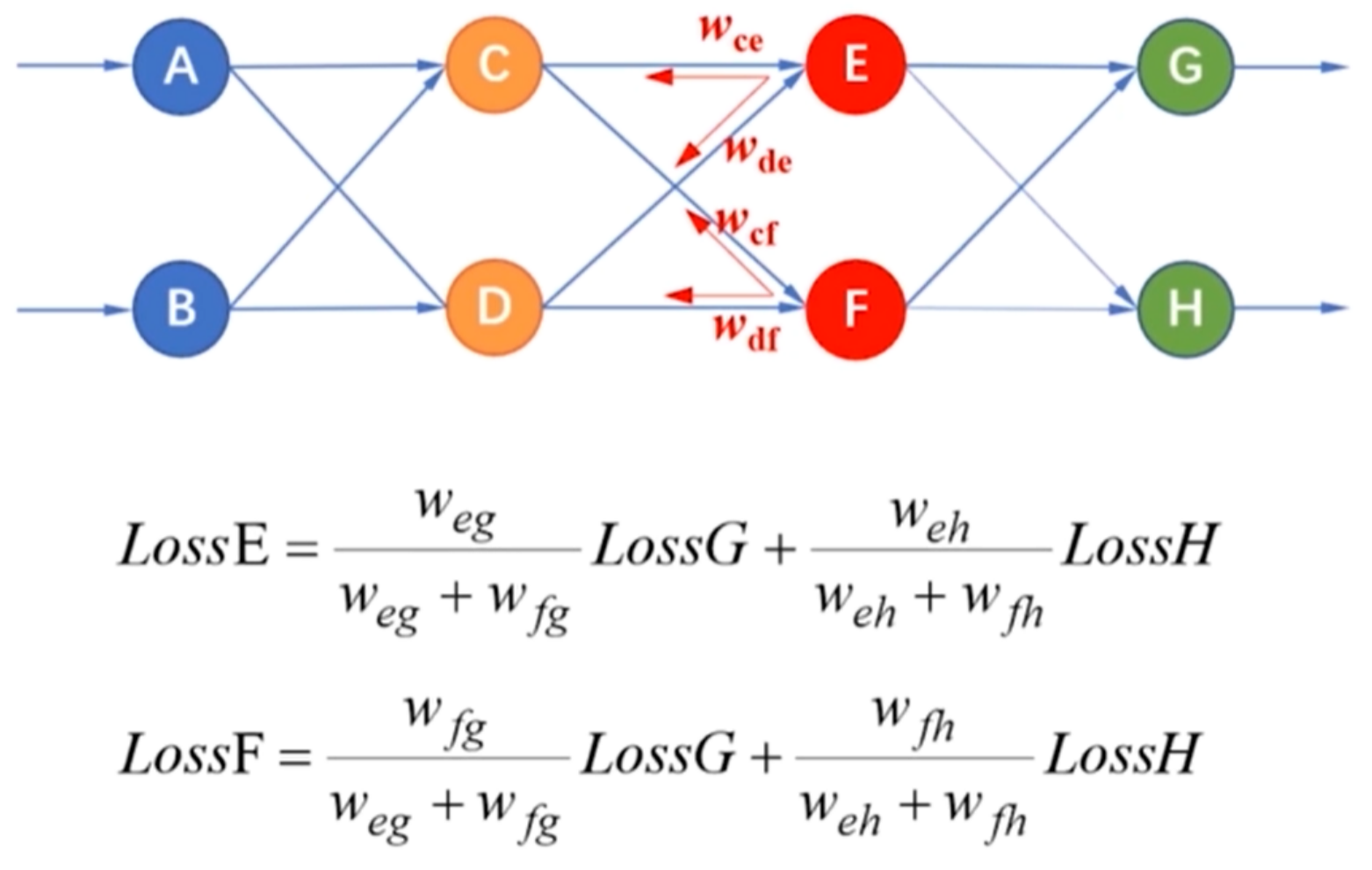
激活函数
1.激活函数的性质
- 简单的非线性函数
- 连续并可导
- 单调函数
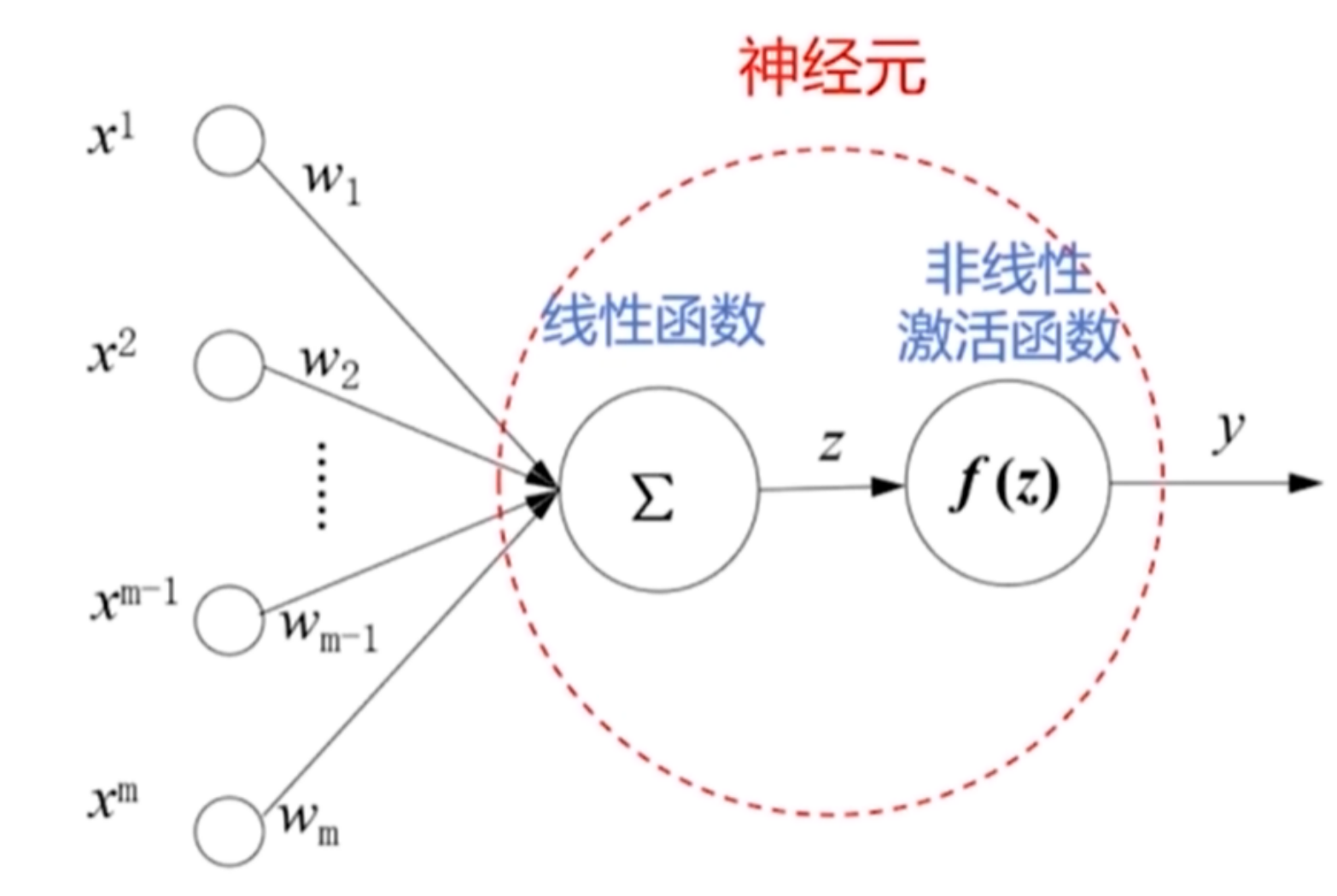
2.常用的激活函数
- logistic函数与Tanh函数
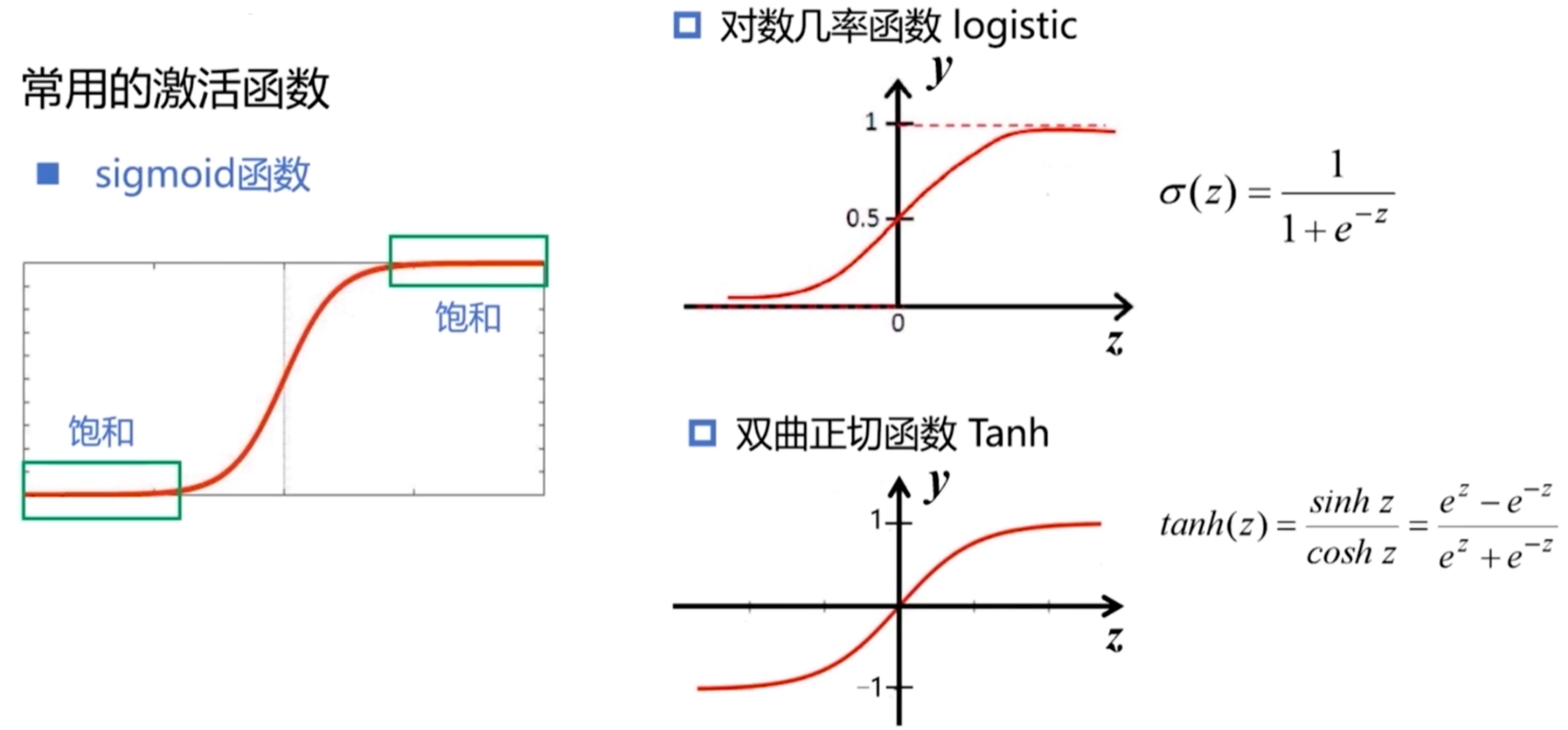
- ReLU函数(Rectified Linear Unit,修正线性单元)
- z>0时,导数等于1,缓解了梯度消失问题
- 不存在幂运算,计算速度快
- 导数恒等于1,训练模型收敛速度快
- 输出不是以0为均值的
- z<0时,梯度为0,神经元死亡
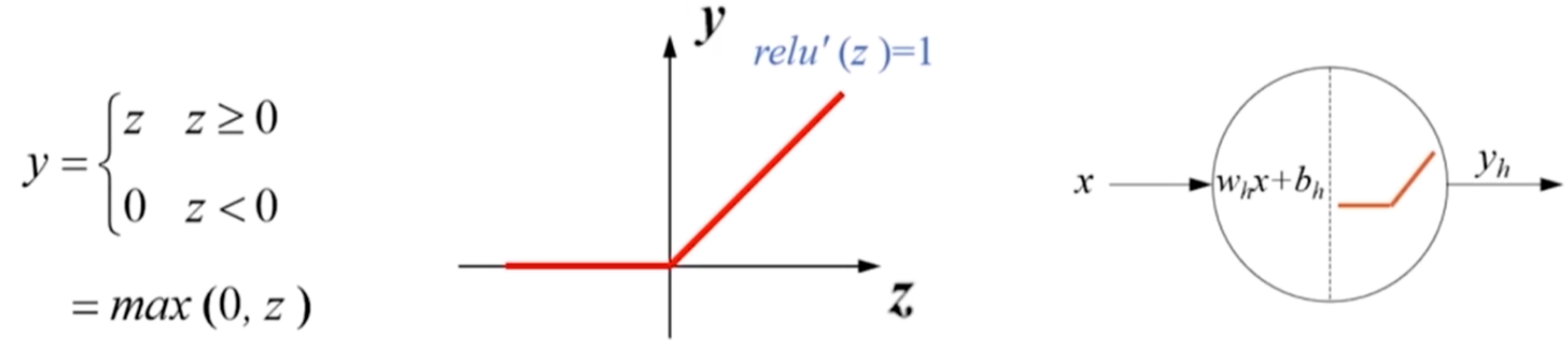
- Leaky-ReLU函数
- 避免了ReLU神经元死亡
- 神经网络的计算和训练速度快
- 超参数a需要人工调整
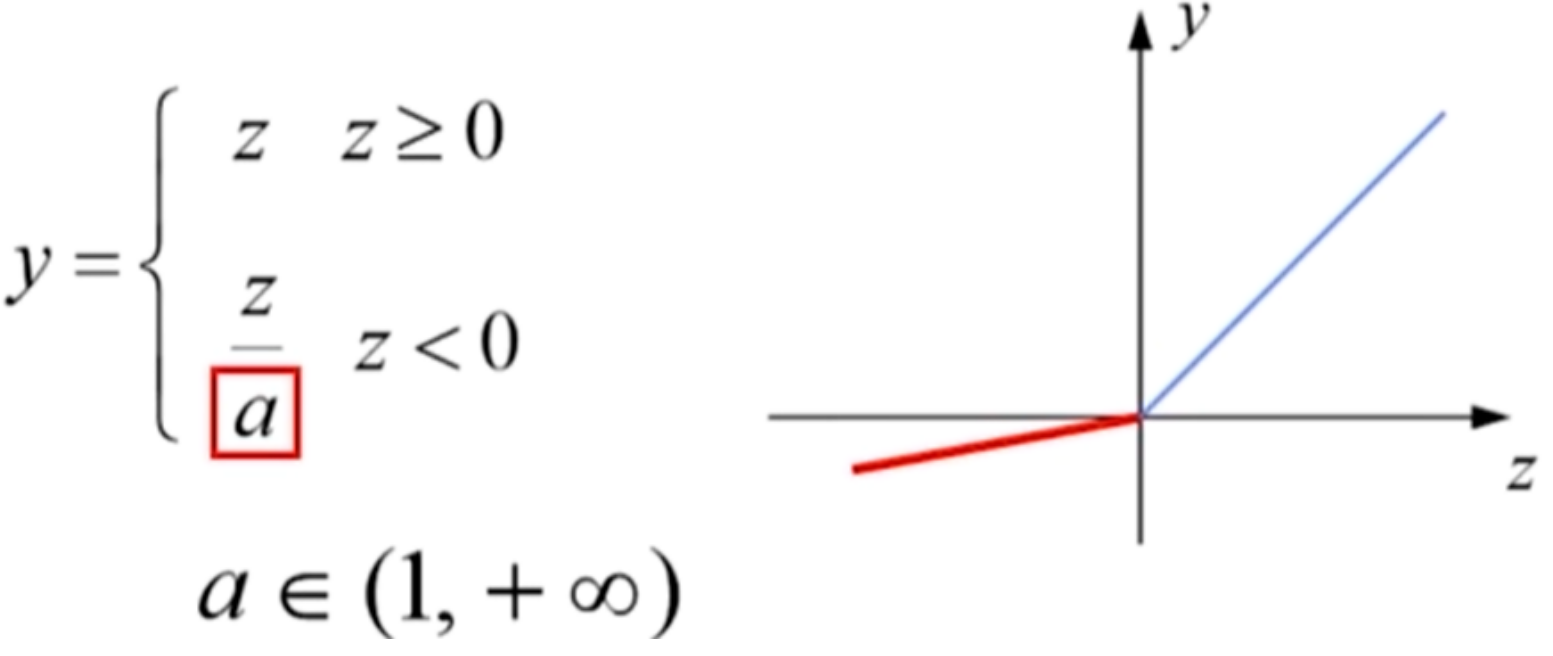
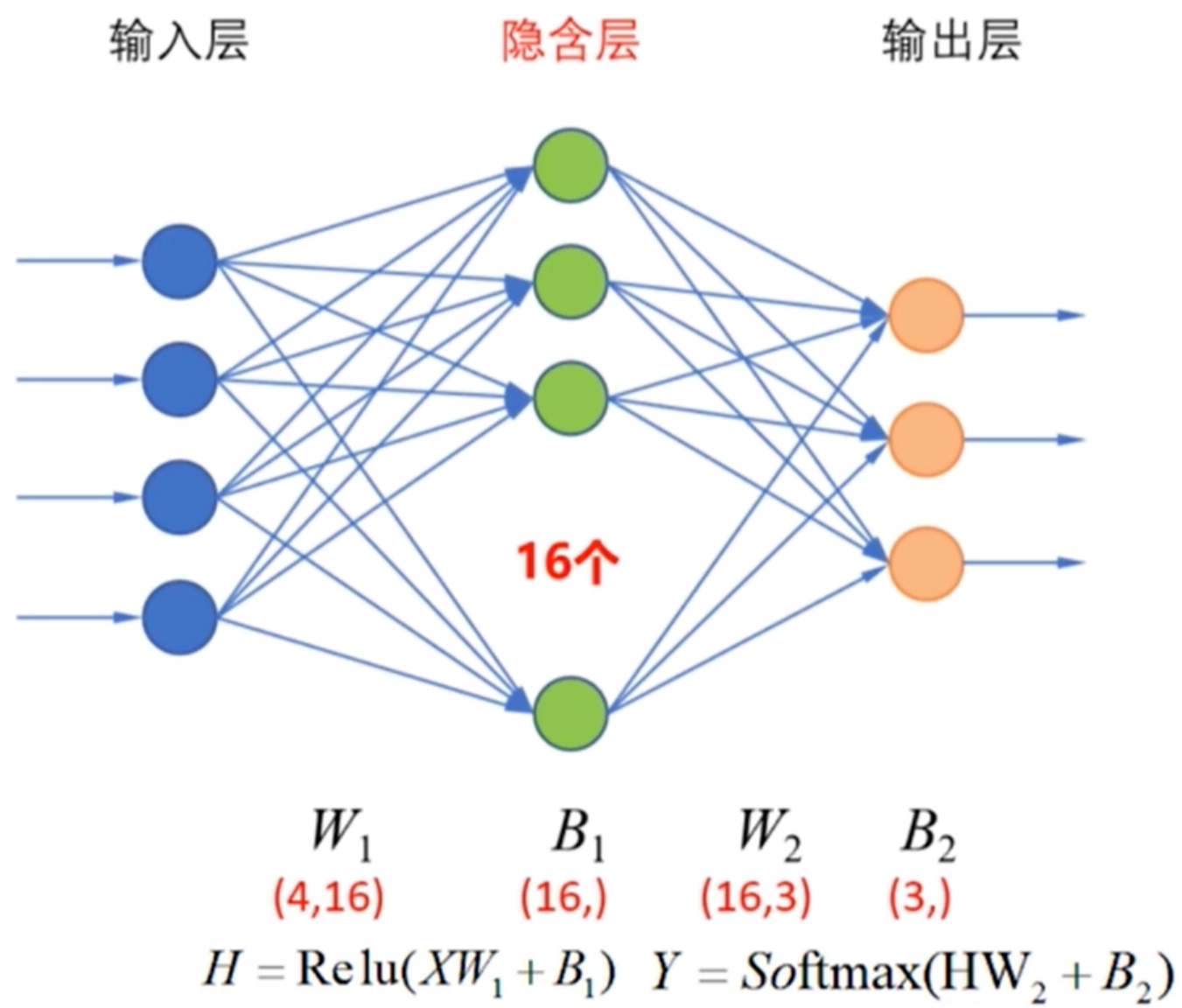
实例:多层神经网络实现鸢尾花分类
思路:
- 隐藏层激活函数:relu函数
- 输出层激活函数:softmax函数
- 损失函数:交叉熵损失函数
- W是属性个数(前一层的输入神经元数)×分类数(本层的个数),B是关于分类数的一维向量
具体代码实现:
1 | #1.导入库,加载数据 |
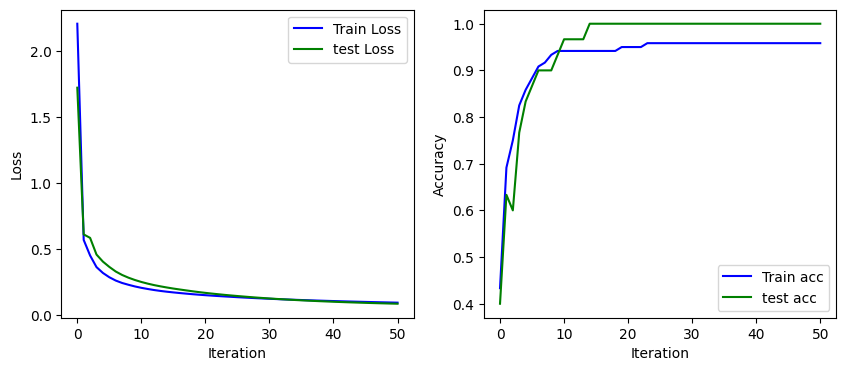
结果如下:
i:0 Train Acc:0.433333 Train Loss:2.205641, Test Acc:0.400000 Test Loss:1.721138
i:10 Train Acc:0.941667 Train Loss:0.205314, Test Acc:0.966667 Test Loss:0.249661
i:20 Train Acc:0.950000 Train Loss:0.149540, Test Acc:1.000000 Test Loss:0.167103
i:30 Train Acc:0.958333 Train Loss:0.122346, Test Acc:1.000000 Test Loss:0.124693
i:40 Train Acc:0.958333 Train Loss:0.105099, Test Acc:1.000000 Test Loss:0.099869
i:50 Train Acc:0.958333 Train Loss:0.092934, Test Acc:1.000000 Test Loss:0.084885
小批量梯度下降法
- 对于多层神经网络,使用梯度下降法,从理论上无法保证一定可以达到最小值
- 使用小批量梯度下降法对其进行改进
- 影响小批量梯度下降法的主要因素:
- 小批量样本的选择:打乱样本
- 批量大小:选择2的幂数,如32、64、128、……
- 学习率
- 梯度
Sequential模型
- 其是一个神经网络框架
- 只有一组输入和一组输出
- 各层按照先后顺序堆叠
1.建立Sequential模型
model=tf.keras.Sequential()
1 | import tensorflow as tf |
结果如下:
<tensorflow.python.keras.engine.sequential.Sequential object at 0x0000014AC0B9FD90>
1.1 添加全连接层
model.add(tf.keras.layers)tf.keras.layers.Dense(inputs,activation,input_shape)- inputs: 本层神经元的个数
- activation: 激活函数(“relu”、”softmax”、”sigmoid”、”tanh”
- input_shape: 输入数据的形状
- 示例:
1 | import tensorflow as tf |
1.2 查看摘要
model.summary()
1 | model.summary() |
结果如下:
Model: "sequential_8"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_15 (Dense) (None, 8) 40
_________________________________________________________________
dense_16 (Dense) (None, 4) 36
_________________________________________________________________
dense_17 (Dense) (None, 3) 15
=================================================================
Total params: 91
Trainable params: 91
Non-trainable params: 0
_________________________________________________________________
2.配置训练方法
model.compile(loss,optimizer,metrics)
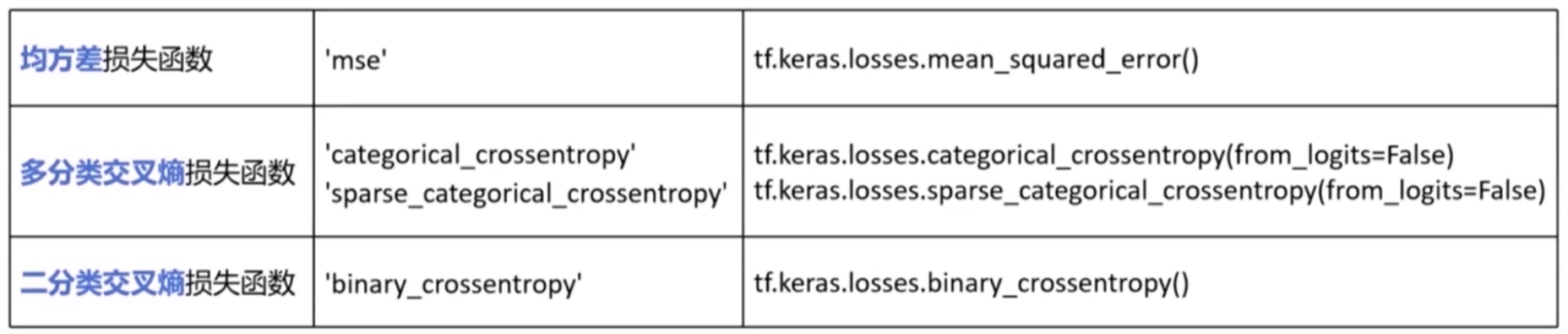
2.1 常用的损失函数loss
- 对于多分类交叉熵损失函数
- 当标签的编码为独热编码时,采用”categorical_crossentropy”
- 当标签的编码为自然顺序码时,采用”sparse_categorical_crossentropy”
- from_logits=False表示神经网络在输出前,已经使用softmax函数将预测结果变成了概率分布,否则设置为True
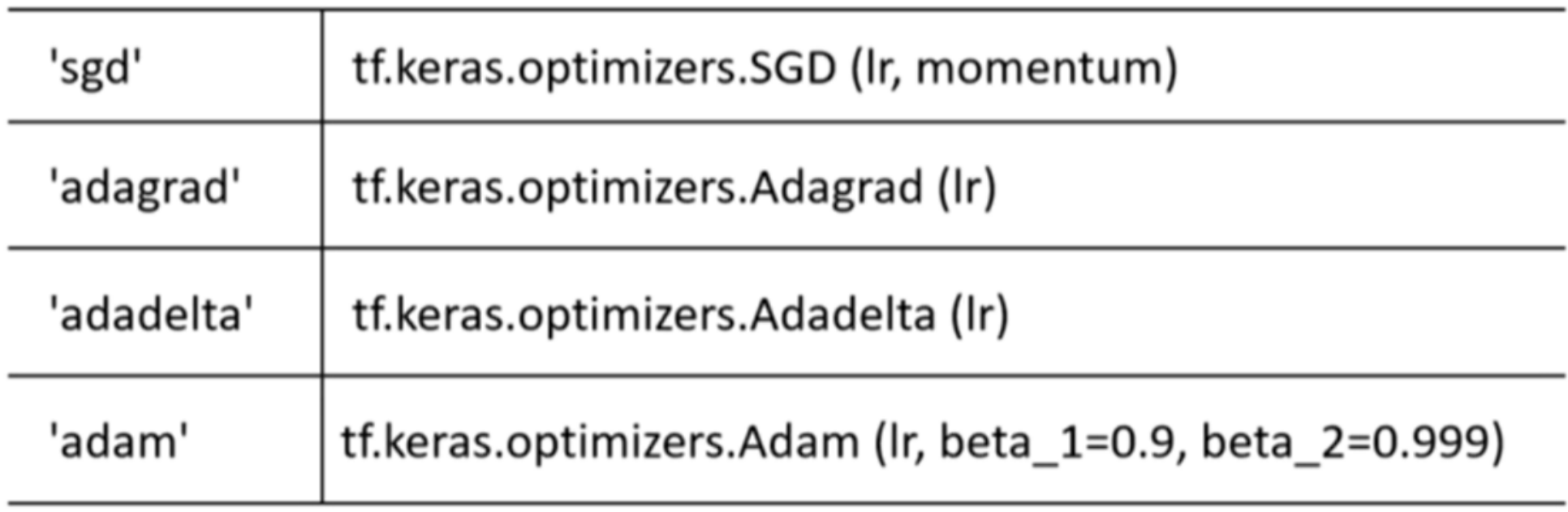
2.2 优化器optimizer
2.3 评估函数metrics
- keras模型性能评估函数
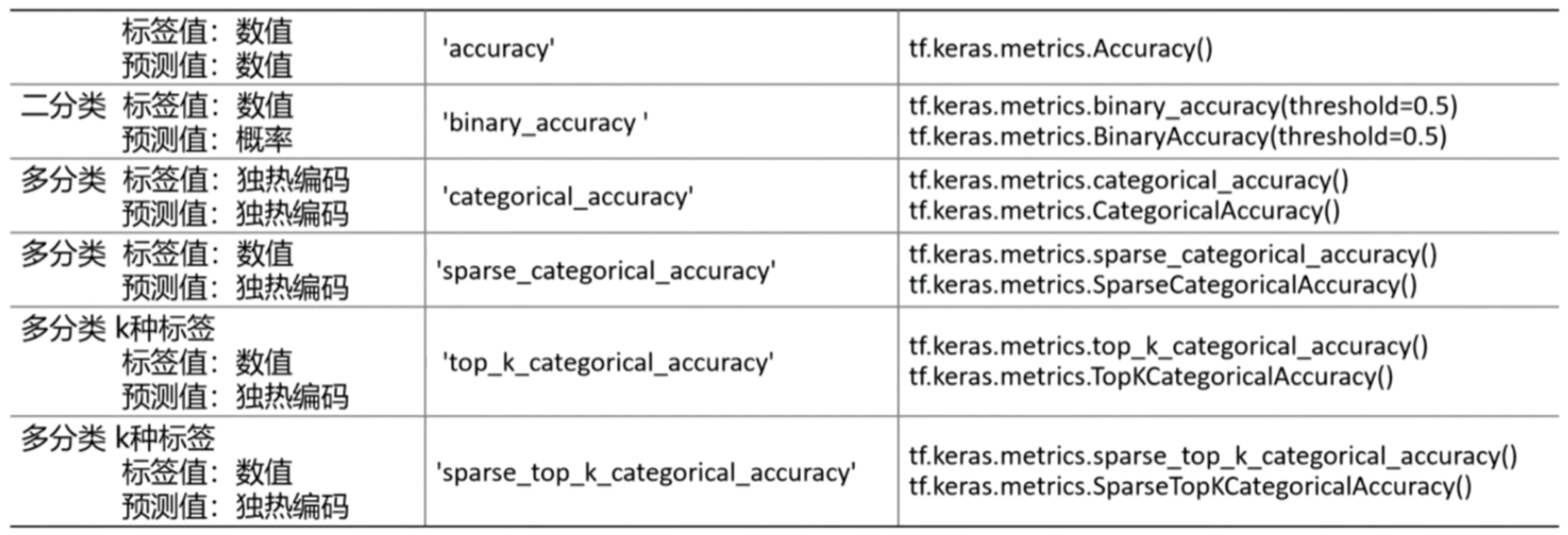
- 可以使用model.metrics_names查看评估函数
3.训练模型
model.fit()- validation_data与validation_split二选一
- validation_freq:每隔多少次训练,使用测试集计算并输出一次评测指标
- verbose:
- =0:不在标准输出流输出
- =1:输出进度条记录
- =2:每个epoch输出一行记录

model.fit()初始值

history=model.fit();history.history- 其以字典的形式分别返回训练集和测试集的损失和准确率
4.评估模型
model.evaluate(test_set_x,test_set_y,batch_size,verbose)
5.使用模型
model.predict(x,batch_size,verbose) #x为数据的属性值
6.模型的保存与加载
仅保存神经网络的模型参数
- 保存:
model.save_weights()#相当于替代了model.fit()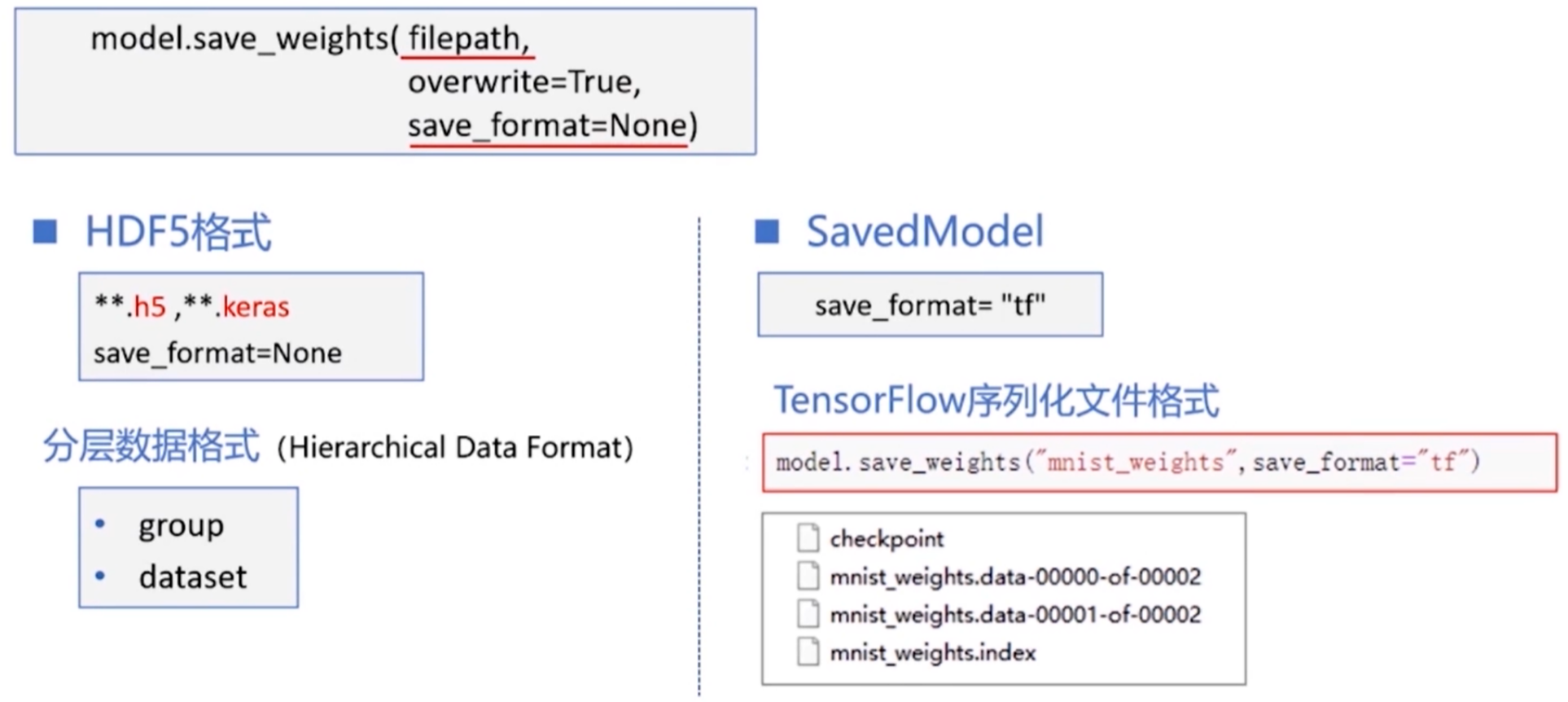
- 加载:
model.load_weights()
1 | model2.save_weights("mnist_save_weights.h5") |
保存整个模型
model.save()
tf.keras.models.load_model()
实例:Sequential实现手写数字识别
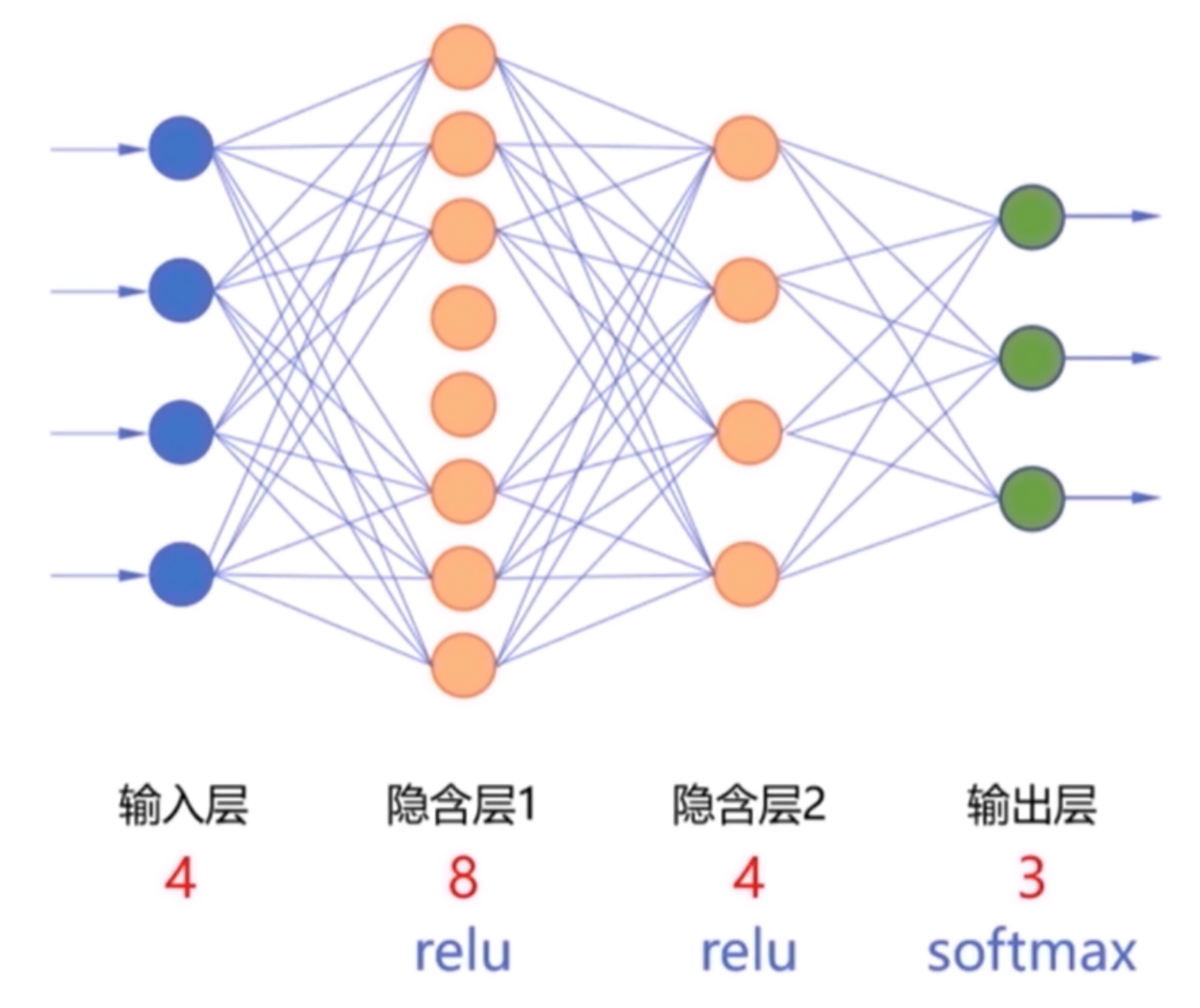
1.设计神经网络结构
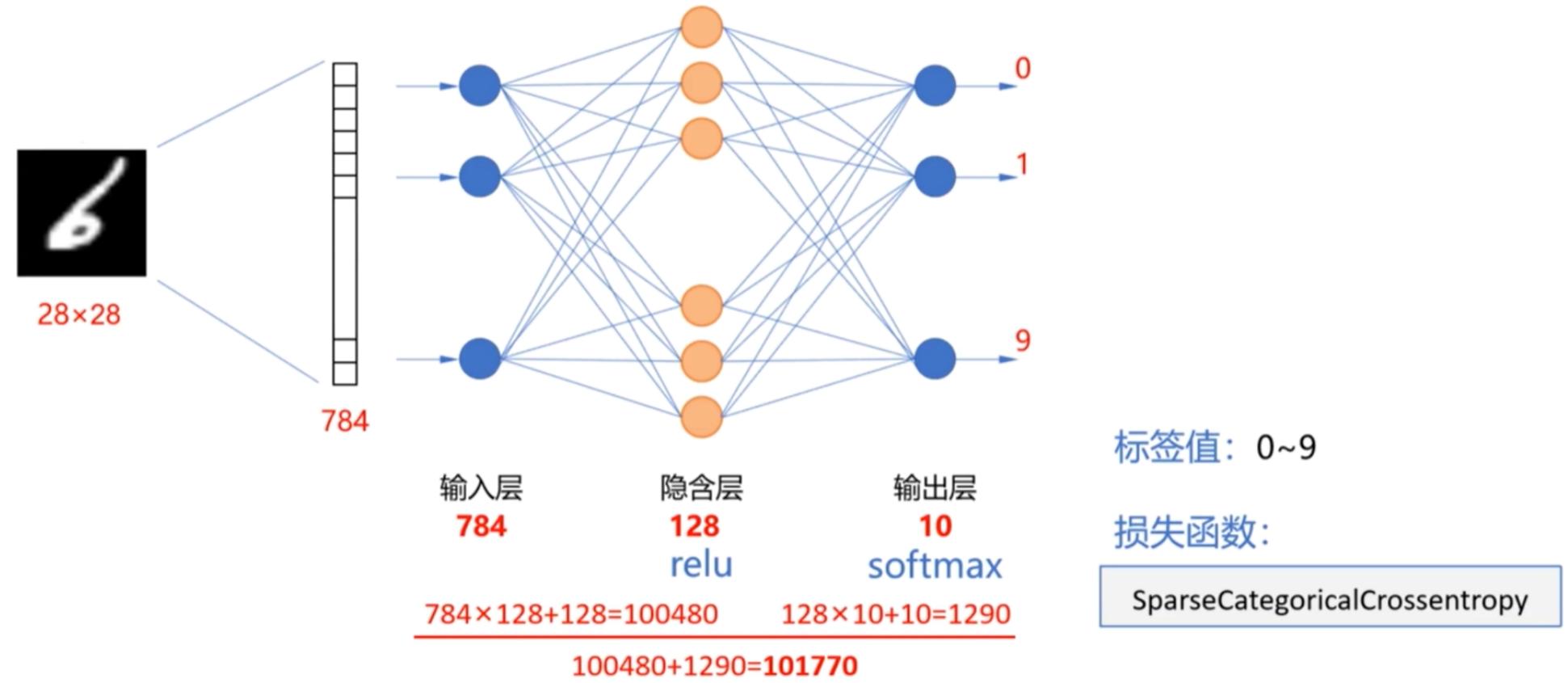
2.代码实现
1 | #1.导入库 |
结果如下:
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_3 (Flatten) (None, 784) 0
_________________________________________________________________
dense_6 (Dense) (None, 128) 100480
_________________________________________________________________
dense_7 (Dense) (None, 10) 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
********************************************************************************
Epoch 1/5
750/750 [==============================] - 4s 4ms/step - loss: 0.3279 - sparse_categorical_accuracy: 0.9079 - val_loss: 0.1745 - val_sparse_categorical_accuracy: 0.9503
Epoch 2/5
750/750 [==============================] - 3s 4ms/step - loss: 0.1517 - sparse_categorical_accuracy: 0.9566 - val_loss: 0.1307 - val_sparse_categorical_accuracy: 0.9626
Epoch 3/5
750/750 [==============================] - 2s 2ms/step - loss: 0.1087 - sparse_categorical_accuracy: 0.9691 - val_loss: 0.1137 - val_sparse_categorical_accuracy: 0.9668
Epoch 4/5
750/750 [==============================] - 1s 1ms/step - loss: 0.0830 - sparse_categorical_accuracy: 0.9752 - val_loss: 0.1081 - val_sparse_categorical_accuracy: 0.9678
Epoch 5/5
750/750 [==============================] - 1s 2ms/step - loss: 0.0649 - sparse_categorical_accuracy: 0.9801 - val_loss: 0.1021 - val_sparse_categorical_accuracy: 0.9694
********************************************************************************
313/313 - 0s - loss: 0.0890 - sparse_categorical_accuracy: 0.9732
********************************************************************************
[[4.3734741e-07 4.9217494e-08 1.3537046e-04 1.3679784e-03 1.0147285e-09
6.0127795e-06 8.5093779e-11 9.9846399e-01 5.7829629e-06 2.0411160e-05]]
7


